Signalverarbeitung mit MATLAB und Künstlicher Intelligenz

Abb. 1: Signalverarbeitung mit MATLAB^® und Künstlicher Intelligenz

Autor:	Moye Nyuysoni Glein Perry
Art:	Project Work
Starttermin:	14.11.2024
Abgabetermin:	31.03.2025
Betreuer:	Prof. Dr.-Ing. Schneider

MindMap

Introductiong

Signal processing has traditionally focused on analyzing, filtering, and interpreting signals in both the time and frequency domains. With the integration of AI, especially deep learning, the possibilities expand to include noise reduction and more. It is essential in many modern applications such as communications, audio and image processing, biomedical signal analysis, and control systems.

Traditionally, classical algorithms have been taught to solve engineering problems. This project solves teaching problems using artificial intelligence and compares these classical algorithms.

Signal Processing Fundamentals

Time Domain vs. Frequency Domain

Time Domain: Time-domain analysis involves studying a signal as it varies over time. However, it might be challenging to extract features such as periodicity or noise characteristics directly from the time domain.

Frequency Domain: Converting a signal into its frequency components (using techniques like the Fourier Transform) often makes it easier to identify and filter out noise, detect repeating patterns, or study signal behavior over various frequency bands.

Signals:

A signal is any piece of information that changes over time or space and can be measured. It may be continuous (analog) or discrete (digital).

Transforms:

Techniques like the Fourier Transform and the Discrete Wavelet Transform decompose signals into constituent frequency (or time-frequency) components for easier analysis.

Filtering:

The process of removing unwanted noise or extracting useful parts of a signal. Techniques include low-pass, high-pass, band-pass, and adaptive filters.

Low Pass Filters: Permit signals with frequencies lower than a cutoff frequency, useful for removing high-frequency noise.

High Pass Filters: Permit frequencies higher than a cutoff frequency, often used to eliminate low-frequency drift or interference.

Band Pass and Band Stop Filters: Focus on specific frequency bands.

cutoff frequency: The cutoff frequency, or cutoff, determines where the signal is cut off. If a signal contains frequencies that range from 500 Hz up to 8000 Hz and the cutoff frequency is set at 4000 Hz, frequencies above 4000 Hz are filtered, for example, in the case of low-pass filters.

Fast Fourier Transform (FFT) and Discrete Cosine Transform (DCT)

FFT: Extracting Frequency Components Purpose: The FFT is used to decompose a signal into its constituent frequency components quickly. It is particularly effective for analyzing periodic signals.

What It Does: Computes the amplitude and phase of frequency components.

DCT: Energy Compaction and Compression Purpose: The DCT transforms a signal into a sum of cosine functions oscillating at different frequencies. It is popular in image and audio compression (e.g., JPEG, MP3) due to its energy compaction properties.

What It Does: Concentrates energy into a few low-frequency coefficients, which is beneficial for compression.

Frequency Over Time: Why Shift to Frequency Analysis?

Working in the frequency domain allows for:

Filtering Unwanted Frequencies: Easily design filters to isolate or remove specific bands.

Feature Extraction: Many machine learning models perform better when provided with frequency domain features rather than raw time signals.

Noise Reduction: Identify and remove noise that might not be apparent in the time domain.

Integrating AI in Signal Processing

AI Enhancements to Signal Processing

Deep learning can extract non-linear and hierarchical features that are often hard to engineer manually. When combined with traditional signal processing:

Preprocessing: Conventional filters and transforms (FFT, DCT) are used to prepare the data.

Feature Extraction: Deep neural networks can build on these features to further identify patterns, such as anomalies in medical signals or fault detection in industrial applications.

Role of Neural Network Layers in Signal Processing

Input Layer

Function:

Receives the preprocessed signal data (it may be raw data or transformed features like FFT coefficients).

Preprocessing:

Normalization and segmentation are done to ensure consistency before feeding into the neural network.

Convolutional Layers

Function:

Commonly employed in image processing, convolutional layers can also extract localized features in time-series data by sliding filters (kernels) over input data.

Signal Processing Connection: In many cases, convolutional filters can learn to mimic traditional filters (e.g., edge detectors or frequency filters).

Activation Functions

Purpose:

Introduce non-linearity into the network.

Common Functions:

ReLU: Effective in mitigating vanishing gradient problems.

Sigmoid/Tanh: Useful for certain tasks but may suffer from saturation in deep networks.

Impact on Training: Ensure that the network learns complex mappings and performs better with non-linear data representations. Pooling Layers

Function:

Downsample the feature maps. For signals, 1D pooling layers can help reduce noise and highlight significant features.

Types:

Max Pooling: Keeps the highest value in a set of features.

Average Pooling: Averages values to retain the overall trend.

Recurrent Layers

Role in Signal Processing: Designed to handle sequential data by maintaining memory across time steps. LSTM (Long Short-Term Memory) and GRU (Gated Recurrent Unit) layers capture temporal dependencies effectively.

Why They Matter: They can model long-term dependencies in signals such as speech or medical time-series data.

Fully Connected Layers

Function:

Integrate and transform features from previous layers into final predictions (classification, regression, etc.).

Mapping: Flatten the features extracted from convolutional or recurrent layers to make a decision based on all gathered information.

Image Processing

Image processing refers to the use of algorithms and computational techniques to analyse, enhance, and manipulate images. It involves altering or improving images using various methods and tools. The main aim of image processing is to improve image quality. Whether it’s enhancing contrast, adjusting colours, or smoothing edges, the focus is on making the image more visually appealing or suitable for further use. It’s about transforming the raw image into a refined version of itself.

Sample Task: Object Detection Identify in an Image

• Classical Method: Circular Objects Detection

• results:

• AI based method: Detect people, cats and dogs in message using YOLO model.

• Results

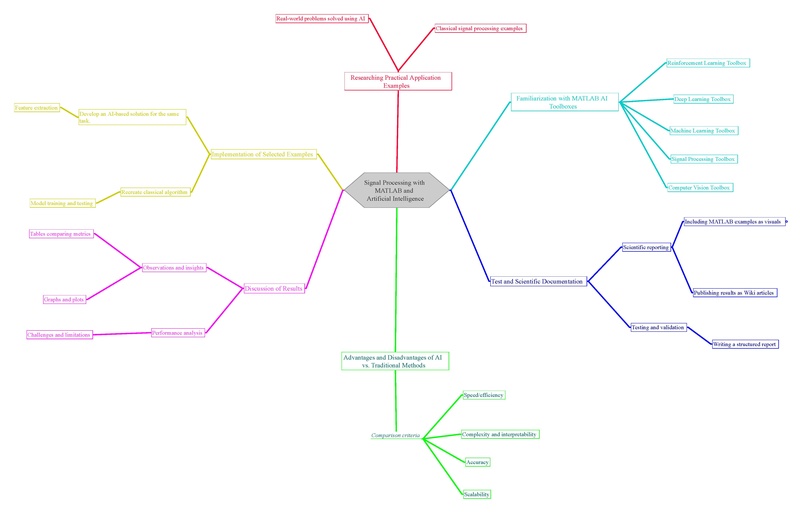
Task

1. Familiarization with MATLAB^® AI toolboxes
2. Researching practical application examples that can be converted to AI
3. Implementation of selected examples
4. Identify the advantages and disadvantages of AI compared to conventional data processing
5. Discussion of the results
6. Test and scientific documentation
7. Providing MATLAB^®-examples as wiki articles

Anforderungen

Das Projekt erfordert Vorwissen in einigen aber nicht allen nachfolgenden Themengebieten. Sollten Sie die Anforderungen nicht erfüllen, kann die Aufgabenstellung mit Blick auf Ihre Vorkenntnisse individuell angepasst werden.

• MATLAB^®/Simulink
• Machine Learning/Deep Learning
• Digitale Signalverarbeitung
• Deep Learning for Image Processing

Anforderungen an die wissenschaftliche Arbeit

• Wissenschaftliche Vorgehensweise (Projektplan, etc.), nützlicher Artikel: Gantt Diagramm erstellen
• Wöchentlicher Fortschrittsberichte (informativ), aktualisieren Sie das Besprechungsprotokoll im Gespräch mit Prof. Schneider
• Projektvorstellung im Wiki
• Tägliche Sicherung der Arbeitsergebnisse in SVN
• Tägliche Dokumentation der geleisteten Arbeitsstunden
• Studentische Arbeiten bei Prof. Schneider
• Anforderungen an eine wissenschaftlich Arbeit

Repository

URL: https://svn.hshl.de/svn/MATLAB_Vorkurs/trunk/Signalverarbeitung_mit_Kuenstlicher_Intelligenz

---

→ zurück zum Hauptartikel: Studentische Arbeiten