SoSe24 - Praktikum Systementwurf - Spurerkennung mit Kamera (Modul OSE)

Abb. 1: Spurerkennung

Autor:	Prof. Dr.-Ing. Schneider
Thema:	Spurerkennung mit Kamera (OSE)
Workshoptermin 9:	20.06.2024
Lernzielkontrolle 3:	04.07.2024

Einleitung

Die Workshops im SDE Praktikum sollen die Studierenden das praktische Arbeiten in einem Mechatroniklabor im Bereich modellbasierte Entwicklung mit MATLAB/Simulink und DSpace Hardware DS1104/ControlDesk vermitteln. Der Umgang soll in der Selbstlernzeit geübt werden.

Im Projekt OSE werden Objekte mit dem LiDAR-Sensor erkannt und verarbeitet sowie die Fahrspur mit der Kamera. Dieser Workshop fokussiert die Spurerkennung sowie die Bildung und des Spurpolynoms.

Lernziele

Nach erfolgreicher Teilnahme am Workshop:

• können Sie die intrinsischen und extrinsischen Parameter einer Kamera bestimmen.
• können Sie eine Inverse Perspektiventransformation durchführen.
• können Sie Fahrbahnmarkierungen segmentieren.
• können Sie das Spurpolynom maßstabsgetreu bestimmen.

Bewertung

Die Bewertung erfolgt im Rahmen der Lernzielkontrolle 3.

Voraussetzungen

• Für den Workshop benötigen Sie MATLAB/Simulink in der Version 2019b.
• Studieren Sie die Praktikumsordnung.
• Die unter Vorbereitung aufgeführten Aufgaben sind vor dem Workshoptermin vorzubereiten. Der Workshop baut auf Ihre Vorbereitung auf.

Der Workshop setzt nachfolgende Kenntnisse voraus:

• die Grundlagen der Programmierung,
• der Umgang mit der Versionsverwaltung SVN und
• der Umgang mit MATLAB/Simulink.
• der Grundlagen der Digitalen Signal- und Bildverarbeitung:
  • Lektion 2: Koordinatentransformationen
  • Lektion 7: Kantenerkennung und Rauschunterdrückung
  • Lektion 8: Datengetriebene Segmentierung

Ablauf des Praktikums

Tabelle 1: Agenda des Workshops

Uhrzeit	Agenda	Form
8:15	Begrüßung	Moderation durch Marc Ebmeyer
8:20	Bearbeitung der Aufgaben (vgl. Tabelle 2)	Gruppenarbeit
10:10	Statusbericht der Teams	max. 5 Min. pro Team
10:25	Verabschiedung	Moderation durch Marc Ebmeyer
10:30 Uhr	Veranstaltungsende

Vorbereitung

Aufgabe 9.1: Vorbereitung der Kamera

Abb. 2: MATLAB^® Camera Calibrator App

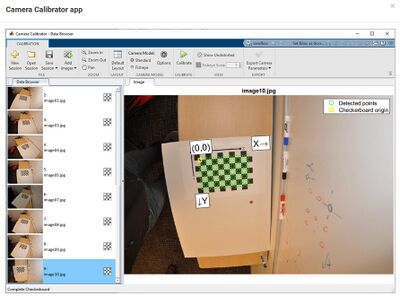
Um eine Kamera sinnvoll zur Spurerkennung einsetzen zu können, muss diese zuvor kalibriert werden.

1. Studieren Sie die zugehörigen Wiki-Artikel und arbeiten Sie sich in die Camera Calibrator App von MATLAB^® ein.
2. Messen Sie die extrinsische und intrinsische Parameter der Kameras von Wagen 1 und 2 mit der MATLAB^® Camera Calibrator App.
3. Identifizieren Sie extrinsische und intrinsische Parameter.
4. Machen Sie ein Foto eines vermessenen Aufbaus.
5. Transformieren Sie einen vermessenen Punkt von Weltkoordinaten in Bildkoordinaten.
6. Machen Sie ein Foto mit der Kamera auf der Fahrbahn von der Startlinie aus (Geradeaus.jpg).
7. Machen Sie ein Foto mit der Kamera auf der Fahrbahn von der ersten Kurve aus (Linkskurve.jpg).
8. Entzerren Sie beide Fotos anhand Ihrer ermittelten k-Matrix mit dem MATLAB^®-Skript entzerreVideobild.
9. Dokumentieren Sie Ihren Versuchsaufbau, die Durchführung und Ergebnisse.

Arbeitsergebnisse:

• Extrinsische Kameraparameter: $[x,y,z]_C, \Phi, \Theta, \Psi$
• Intrinsische Kameraparameter: k-Matrix
• Eingangsdaten: Geradeaus.jpg, Linkskurve.jpg
• MATLAB^®-Skript entzerreVideobild, welches anhand der intrinsischen Kameraparameter die Bildentzerrung durchführt.
• Versuchsprotokoll Kamerakalibrierung.docx

Lernzielkontrollfragen:

• Welche intrinsischen und extrinsischen Kameraparameter haben Wagen 1 und 2?
• Welchen Region-of-Interest (ROI) haben die Kameras?
• Wie ist der Zusammenhang zwischen Welt- und Bildkoordinaten?
• Welchen Blindbereich in Fahrzeugkoordinaten haben Wagen 1 und 2 ($x_F$)?

Links

• HSHL-Wiki: Kalibrierung_der_Kamera
• MATLAB^® Camera Calibrator App
• OSE:_Bildverarbeitung_mit_Spurerkennung

Tipps 

• Das Schachbrett zur Kalibrierung existiert bereits im Labor.
• Bei der Bilderreihe muss das Schachbrettmuster den gesamten Bildbereich abdecken.
• Legen Sie das Schachbrett flach auf den Boden und vermessen Sie die Position in Bezug auf die Kamera mit einem Maßband. So können Sie Lage und Pose der verbauten Kamera in MATLAB^® ablesen.

---

Aufgabe 9.2: Segmentierung der Fahrbahnmarkierungen

Abb. 3: Geradeausfahrt (Frame 40)

Abb. 4: leichte Linkskurve (Frame 160)

Abb. 5: scharfe Linkskurve (Frame 350)

1. Laden Sie das Bild Spurkandidaten_F040.png (vgl. Abb. 3).
2. Segmentieren Sie aus dem Kantenbild die rechte Fahrbahnmarkierungen. Welche Algorithmen der Vorlesung "Digitale Signal und Bildverarbeitung" lassen sich anwenden?
3. Zeigen Sie das Segment farbig im Bild an.
4. Verifizieren Sie Ihren Segmentierungsalgorithmus mit den Bildern Spurkandidaten F160.png und Spurkandidaten F350.png.

Eingangsdateien:

• Medium:Spurkandidaten F040.png
• Medium:Spurkandidaten F160.png
• Medium:Spurkandidaten F350.png

Arbeitsergebnisse:

• Segmentierung der X-Y-Daten der rechten Fahrspuren für die unterschiedlichen Eingangsdateien mit dem Skript segmentiereFahrbahnmarkierung.m.
• Segmentmaske als Mat-Datei z. B.Spurkandidaten F040.mat.

Lernzielkontrollfragen:

• Welche Methoden kennen Sie aus der Vorlesung "Digitale Signal- und Bildverarbeitung", um eine Fahrspur zu segmentieren? Stellen Sie 5 unterschiedliche Ansätze vor.
• Welche Merkmale sind für eine Fahrspur signifikant.
• Welche Fehlereinflüsse gibt es? Wie kann man diesen entgegenwirken?

Tipp 1 

1. Nutzen Sie bwlabel um zusammenhängende Gebiete segmentieren.
2. Wählen Sie das räumlich nächste Segment rechts der Bildmitte (376,531).
3. Speichern Sie das Segment als Maske in eine mat-Datei.
4. Färben Sie mit der Maske Ihr Ergebnis ein.

Tipp 2: Einfärben der Fahrspur 

stDateiname = 'Spurkandidaten_F040.png';
aFrame = uint8(imread(stDateiname)); % Bild laden
load([stDateiname(1:end-3),'mat']);  % Spurkandidaten laden
R = 255 * aFrame;
G = 255 * aFrame;
B = 255 * aFrame;
B = B.*uint8(~aRechteFahrspur); % Maske anwenden
aRGBBild = cat(3, R, G, B);     % RGB-Bild erzeugen
imshow(aRGBBild);

Musterlösung 

Abb. 6: Segmentierung der Fahrspuren

Programmablaufplan 

Abb. 7: PAP der Fahrspursegmentierung

---

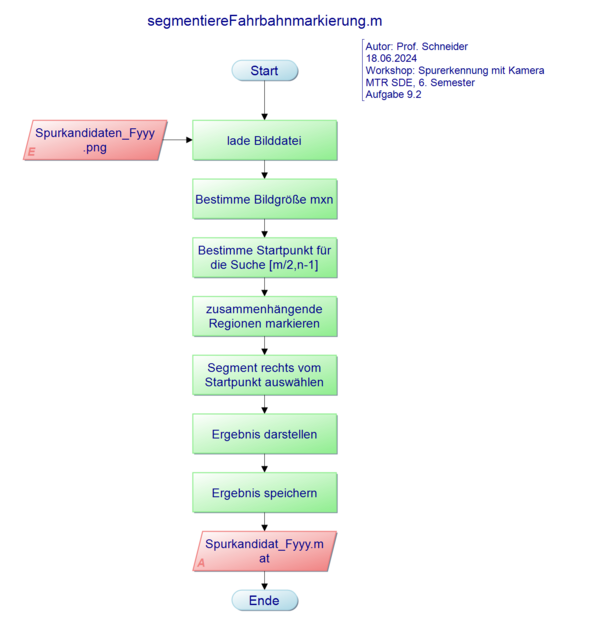Aufgabe 9.3: Spurpolynom

Abb. 8: Darstellung der Fahrspuren als Polynom

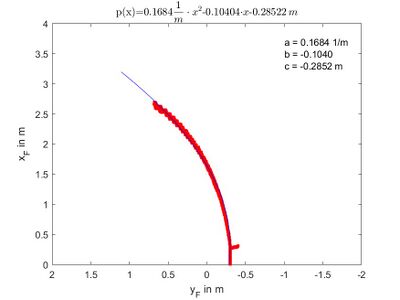
1. Bestimmen Sie für die rechte Fahrbahnmarkierungen das Spurpolynome 2. Ordnung mit polyfit.
2. Ersetzen Sie polyfit durch die einfache Polynomapproximation interpoliereFahrspur.m.
3. Berechnen Sie aus dem Spurpolynom die rechte Fahrbahnmarkierungen.
4. Blenden Sie die rechte Fahrbahnmarkierungen im Videobild für die Bildframes 40, 160 und 350 ein.

Demo: https://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/Software/Demos/Lane_Tracking

Eingangsdaten:

• Medium:Spurkandidaten.zip
• interpoliereFahrspur.m als Alternative zu polyfit

Arbeitsergebnis: Spurpolynome für die Bildframes 40, 160 und 350, visuelle Überprüfung durch Einblendung in die Bilddateien zeigeSpurpolynom.m (vgl. Abb. 8)

Lernzielkontrolle:

• Wie lauten die Umrechnungsfaktoren Pixel in m in xF- und yF-Richtung.
• Welche Vor- und Nachteile hat die Polynombildung?
• Wie könnten die Nachteile behandelt werden?
• Wie wird der Blindbereich vorm Fahrzeug berücksichtigt?

Dokumente:

• Lastenheft_Autonomes_Fahrzeug.pdf
• Schnittstellendokumentation_Anlage_Lastenheft.docx

Tipps  Wandeln Sie die Maske mit find in einen Vektor. Die Koordinatentransformation Bild- zu Fahrzeug-KOS besteht aus einer Verschiebung und der Umrechnung Pixel zu m. Informationen zu den KOS finden Sie in den Dokumenten Lastenheft_Autonomes_Fahrzeug.pdf und Schnittstellendokumentation_Anlage_Lastenheft.docx. Nutzen Sie für die Polynomregression polyfit und alternativ interpoliereFahrspur.m.

Verwenden Sie die LaTeX-Notation im Titel.

title(['p(x)=',num2str(p(1)),'$$\frac{1}{m} \cdot x^2 + $$',num2str(p(2)),'$$ \cdot x + $$',num2str(p(3)),'$$\,m$$'],'interpreter','latex')

Programmablaufplan 

Abb. 9: PAP der Polynomregression

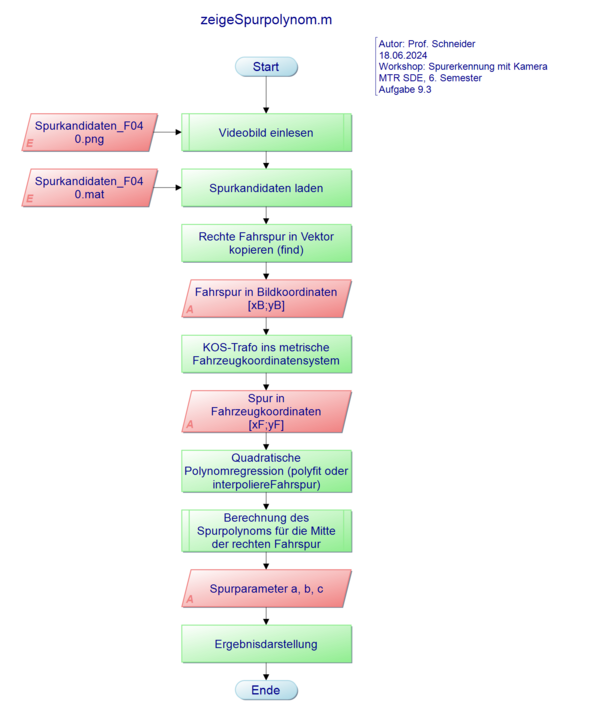Durchführung

Themen der Teams

Tabelle 2: Teameinteilung und Themen

#	Thema	Teilnehmer
1	9.4 Inverse Perspektiventransformation (IPT)	Daniel Block, Paul Janzen
2	9.5 Segmentierung der Fahrbahnmarkierungen	Dennis Fleer, Philipp Sander
3	9.6 Spurpolynom	Yunkai Lin, Xiangyao Liu, Yuhan Pan

Aufgabe 9.4: Inverse Perspektiventransformation (IPT)

1. Studieren Sie den Artikel zur Inversen Perspektiventransformation mit MATLAB^®.
2. Beschreiben Sie die Eingangsparameter. Nutzen Sie die Parameter aus Aufgabe 9.1.
3. Beschreiben Sie die Ausgangsparameter.
4. Kalibrieren und Entzerren Sie das Kamerabild. Weisen Sie den Erfolg mit einem Referenzbild nach.
5. Wenden Sie die IPT auf das Video GeradeInKurve.mp4 an.
6. Binarisieren Sie das Video und speichern Sie es als GeradeInKurve_IPT.mp4.
7. Analysieren Sie Ihr Ergebnis, identifizieren Sie Probleme und entwickeln mögliche Maßnahmen. Eine Umsetzung der Maßnahmen ist nicht erforderlich.

Eingangsdateien:

• SVN: GeradeInKurve.mp4
• Kalibrierparameter der Kamera(s) aus Aufgabe 9.1.

Arbeitsergebnisse:

• MATLAB^®-Skript: startInversePerspektivenTransformation.m
• Transformiertes Video: GeradeInKurve_IPT.mp4
• Dokumentation im Wiki-Artikel

Lernzielkontrollfragen:

• Wofür werden die Kamerakalibrierparameter verwendet?
• Was ist ein region-of-interest (ROI)? Wie wird dieser gewählt?
• Wie führt man eine effektive Binarisierung durch?
• Welche Fehler zeigen sich im Binärbild? Wie lassen sich diese beheben?

Tipps  Nützliche MATLAB^®-Befehle: monoCamera, birdsEyeView, VideoWriter, hasFrame, readFrame, undistortImage, transformImage, im2frame, writeVideo, open, close Nutzen Sie die Color Thresholder App für die Binarisierung. Nutzen Sie die MATLAB^®-Funktion transformImage für die IPT.

Beispiel: Bilder als Video speichern. 

hAusgabeVideo = VideoWriter('GeradeInKurve_IPT.mp4','MPEG-4');
hAusgabeVideo.FrameRate = 30;
hAusgabeVideo.Quality   = 90;
open(hAusgabeVideo)
aFrame = im2frame(uint8(aBild),colormap(gray(2))); % Bild in Frame wandeln
writeVideo(hAusgabeVideo,aFrame);
close(hAusgabeVideo)

Programmablaufplan 

Abb. 10: PAP der Inverse Perspektiventransformation

---

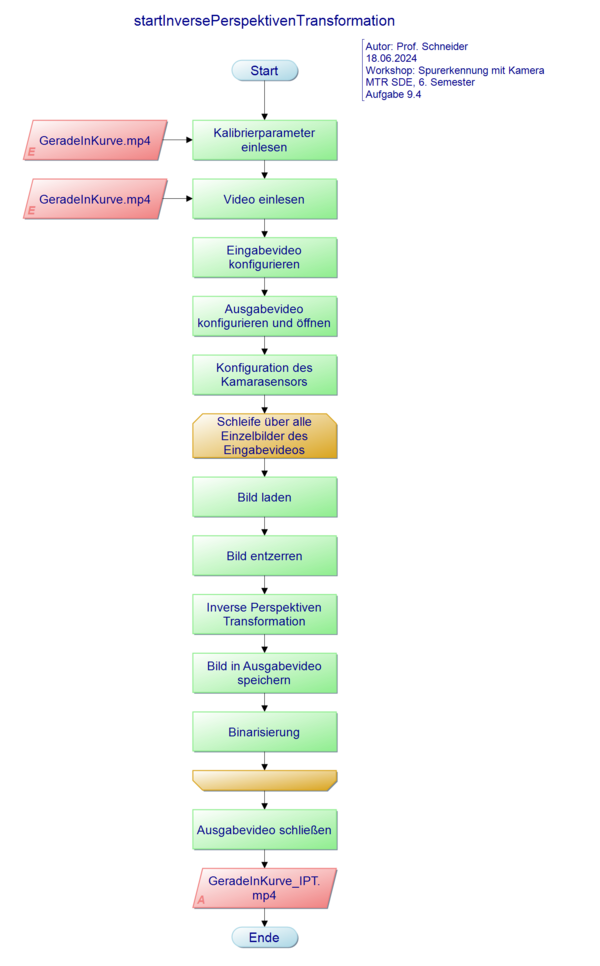Aufgaben 9.5: Segmentierung der Fahrbahnmarkierungen

Abb. 10: Segmentierung der Fahrspuren in GeradeInKurve_Segmente.mp4

1. Segmentieren Sie die drei Fahrspuren aus dem Video GeradeInKurve_IPT.mp4.
2. Zeigen Sie dieses Segmente in den Farben laut Tabelle 3 im Video an (vgl. Abb. 10).
3. Sichern Sie das Ergebnisvideo.
4. Analysieren Sie Ihr Ergebnis, identifizieren Sie Probleme und entwickeln mögliche Maßnahmen. Eine Umsetzung der Maßnahmen ist nicht erforderlich.

Tabelle 3: Farbcodierung der Fahrbahnen

rechte Fahrbahnmarkierung	Gelb (y)
Mittelstreifen	Rot (r)
linke Fahrbahnmarkierung	Grün (g)

Eingangsdateien: GeradeInKurve_IPT.mp4

Arbeitsergebnisse:

• MATLAB^®-Skript: segmentiereFahrbahnmarkierungen.m
• Darstellung des Fahrspursegmente für jedes Einzelbild des Films.
• Visuelle Überprüfung durch Einblendung in das Ergebnisvideo: GeradeInKurve_Segmente.mp4
• Sicherung der Segmente in GeradeInKurve_Segmente.mat
• Dokumentation im Wiki-Artikel

Lernzielkontrolle:

1. Mit welchen Ansätzen lassen sich die Mittle- und rechte Fahrspur segmentieren?
2. Wieso sollten alle Fahrbahnränder segmentiert werden?
3. Welche Vor- und Nachteile hat die Segmentierung?
4. Wie könnten die Nachteile behandelt werden?

Tipps  Nützliche MATLAB^®-Befehle: VideoReader hasFrame, readFrame, bwlabel, regionprops Sobald Sie eine Spur gefunden haben, können Sie parallel dazu die anderen Markierungen suchen. Mit regionprops können Sie die Position der Segmente berechnen.

Beispiel: cell-array der Fahrspurmasken erzeugen  

Segment(:,:,1)=aLinkeFahrspur;
Segment(:,:,2)=aMittelFahrspur;
Segment(:,:,3)=aRechteFahrspur;
Fahrbahnmarkierung{nBild}=Segment;

Beispiel: Mittelpunkt der Unterkante eines Segmentes berechnen 

[Label,nAnzahlSegmente] = bwlabel(aFrameBW); % Segmente labeln
s=regionprops(Label,'Extrema'); % Segmentmerkmale bestimmen
for i=1:nAnzahlSegmente
    p1 = s(i).Extrema(5,:); % Unten-Rechts
    p2 = s(i).Extrema(6,:); % Unten-Links
    p = (p1+p2)/2;          % Unten-Mitte
    SegmentPosition(i,:) = p;
end

Beispiel: Segmente anhand einer Maske einfärben  

aBild = zeros(480,640,3); % Beispielbild

aMaske = zeros(480,640,1,'logical'); aMaske(:,300:305) = 255; % Vertikaler Strich als Maske

% Zerlegung in RGB Farbkanäle
R = aBild(:,:,1); % Rotkanal
G = aBild(:,:,2); % Rotkanal
B = aBild(:,:,3); % Rotkanal

% Einfärben mit Maske
R(aMaske)=255;

aRGB = cat(3,R,G,B);

Programmablaufplan 

Abb. 11: PAP der Segmentierung der Fahrbahnmarkierungen

---

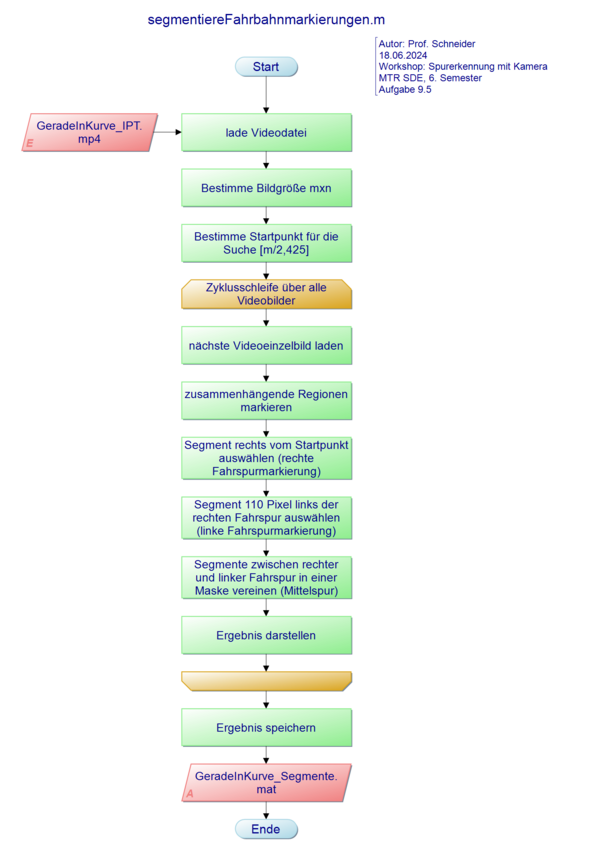Aufgaben 9.6: Spurpolynom

Abb. 12: Darstellung der Fahrspuren als Polynom in GeradeInKurve_Spurpolynom.mp4

1. Bestimmen Sie für die drei Spursegmenten die Spurpolynome 2. Ordnung mit interpoliereFahrspur.m gemäß Schnittstellendokumentation_Anlage_Lastenheft.docx metrisch im Fahrzeugkoordinatensystem.
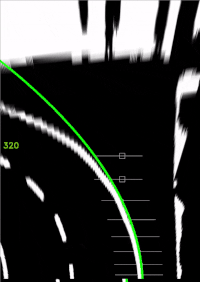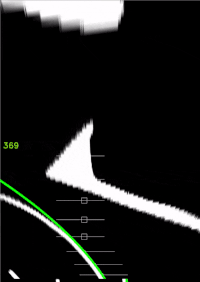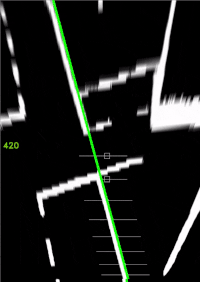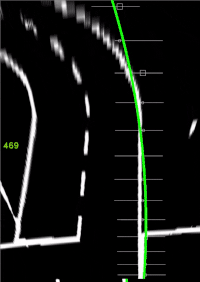
2. Blenden Sie die Spurpolynome in den Farben laut Tabelle 3 im Video GeradeInKurve_IPT.mp4 ein (vgl. Abb. 12 und 14).
3. Bestimmen Sie das laut Schnittstellendokumentation_Anlage_Lastenheft.docx zu ermittelnde Spurpolynom für die Querregelung.
4. Zeichnen Sie dieses als weiße Parabel ein (vgl. Abb. 12 und 14).
5. Zeigen Sie das metrische Spurpolynom in Fahrzeugkoordinaten an (vgl. Abb. 15).
6. Sichern Sie das Ergebnisvideo.
7. Sichern Sie die Spurparameter des Spurpolynoms für die Querregelung.
8. Analysieren Sie Ihr Ergebnis, identifizieren Sie Probleme und entwickeln mögliche Maßnahmen. Eine Umsetzung der Maßnahmen ist nicht erforderlich.

Eingangsdateien:

• GeradeInKurve_IPT.mp4
• GeradeInKurve_Segmente.mat: struct mit den Labelmasken Linke Spur, Mittelspur, rechte Spur
• zeigeSegmente.m: Hilfsfunktion zum Anzeigen der Segmente
• interpoliereFahrspur.m: Hilfsfunktion zur Polynomregression

Arbeitsergebnisse:

• MATLAB^®-Skript: zeigeSpurpolynom.m
• Darstellung des Spurpolynoms für jedes Einzelbild des Films.
• Visuelle Überprüfung durch Einblendung in das Ergebnisvideo: GeradeInKurve_Spurpolynom.mp4
• Spurparameter [a b c] als Spurpolynom.mat
• Dokumentation im Wiki-Artikel

Lernzielkontrolle:

1. Wie lassen sich die Spurpolynome für die 3 Segmente bestimmen.
2. Welche Vor- und Nachteile hat die Polynombildung?
3. Wie könnten die Nachteile behandelt werden?
4. Wie lauten die Umrechnungsfaktoren Pixel in m in xF- und yF-Richtung.
5. Wie wird der Blindbereich vorm Fahrzeug berücksichtigt?
6. Wie wird das Spurpolynom für die Querregelung aus den Spurpolynom der Fahrbahnmarkierungen ermittelt?

Tipps  Nützliche MATLAB^®-Befehle: VideoReader hasFrame, readFrame, find, text Das Spurpolynom für die Regelung hat seinen Ursprung im fahrzeugfesten Koordinatensystem im Mittelpunkt des Stoßfängers vorn. Das Video hat hier einen Blindbereich da die Kamera hinten verbaut wurde. Diese Strecke muss vermessen und als Ursprung der Parabel berücksichtigt werden. Das Spurpolynom für die Regelung muss aus den Spurpolynomen für die Fahrbahnmarkierungen ermittelt werden. Beachten Sie dabei die Krümmung in den Kurven.

Programmablaufplan 

Abb. 13: PAP der Polynomregression der Fahrbahnmarkierungen

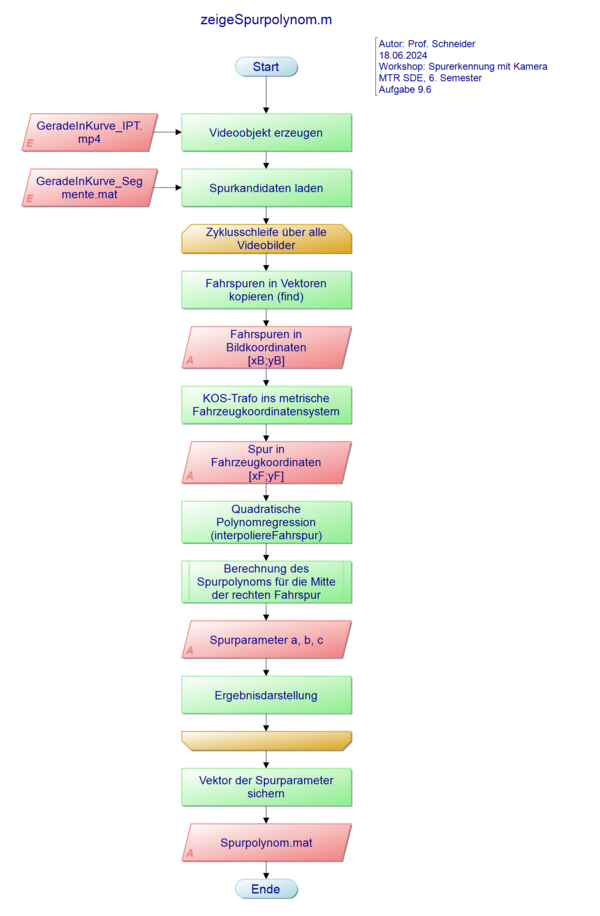Musterlösung 

Abb. 14: Darstellung der Spurpolynome in Bildkoordinaten

Abb. 15: Metrische Darstellung der Spurpolynome in Fahrzeugkoordinaten

---

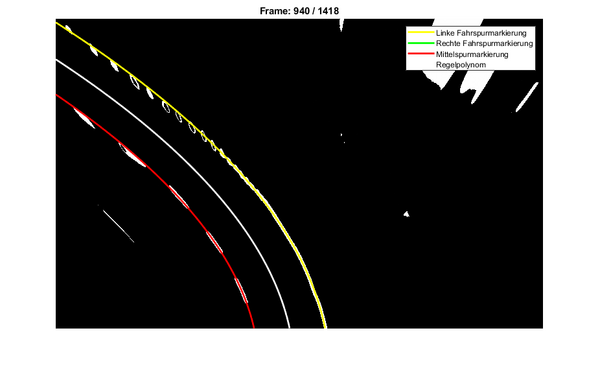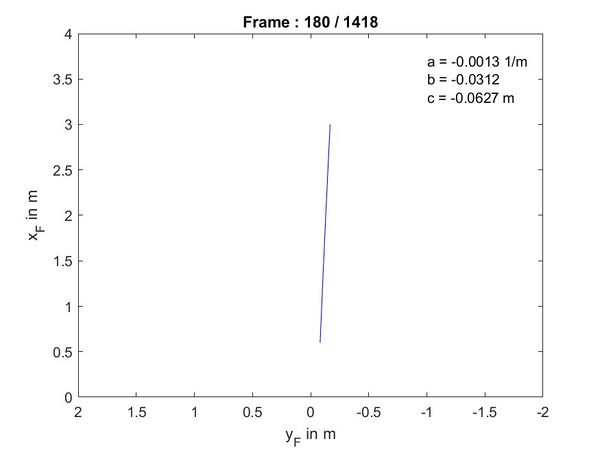Nützlicher Link

• Allgemeine Anforderungen an ein Versuchsprotokoll
• MATLAB^®-Skript, welches die Messung in eine Auswertedatei umwandelt: funktion_wandle_dspacemess_in_CCF_mess.m

---

→ zurück zum Hauptartikel: Praktikum SDE | SDE-Team 2024/25