SoSe24 - Praktikum Systementwurf - Spurpolynom
| Autoren: | Yuhan Pan, Xiangyao Liu, Yunkai Lin |
| Thema: | Spurpolynom |
| Workshoptermin 9: | 20.06.2024 |
| Lernzielkontrolle 3: | 04.07.2024 |
Einleitung
In diesem Workshop lernen Sie, wie Bilddaten von Fahrzeugkameras verarbeitet werden, um Fahrspuren zu erkennen und zu analysieren. Der Fokus liegt auf der Transformation von Bildkoordinaten in Fahrzeugkoordinaten und der Erstellung von Polynomen zur Darstellung der Fahrspur. Zudem wird die Berücksichtigung des Blindbereichs und die Ermittlung der Mittellinie für die Querregelung behandelt.
Spurpolynom
In diesem Abschnitt werden die grundlegenden Konzepte und Techniken zur Ermittlung von Spurpolynomen erläutert. Dies umfasst die Theorie der Polynombildung, die Transformation von Bild- zu Fahrzeugkoordinaten, die Berücksichtigung des Blindbereichs sowie die Ermittlung des Spurpolynoms für die Querregelung.
Beschreibung die Theorie der Polynombildung
Die Polynombildung ist ein Verfahren zur Annäherung oder Interpolation von Datenpunkten durch ein Polynom. Ein Polynom n-ten Grades hat die Form: Die Koeffizienten werden so bestimmt, dass die Summe der quadrierten Abweichungen minimiert wird (Methode der kleinsten Quadrate). Im diese Workshop wurden Spurpolynom in Form: zeigen. Man kann durch den Segmentierung der Spurpolynom von Video der Queranzahl x und y festlegen, und durch den Queranzahl y und x den Spurparameter a, b und c berechnen.
Beschreiben Sie die KOS-Trafo Bild- zu Fahrzeugkoordinaten
Die KOS-Transformation wandelt Bildkoordinaten (u, v) in Fahrzeugkoordinaten (X, Y, Z) um. Zuerst werden Bildkoordinaten in Kamerakoordinaten umgerechnet, dann werden diese in Fahrzeugkoordinaten transformiert unter Berücksichtigung der Kameraposition und -neigung.
Berücksichtigung des Blindbereichs
Der Blindbereich umfasst Bereiche, die von der Kamera nicht erfasst werden können. Um den Blindbereich zu berücksichtigen, werden nur sichtbare Bereiche des Bildes in die Fahrzeugkoordinaten transformiert und weiterverarbeitet, indem sie geometrisch berechnet und maskiert werden.
Wie wird das Spurpolynom für die Querregelung aus den Spurpolynomen der Fahrbahnmarkierungen ermittelt?
Das Spurpolynom für die Querregelung wird aus den Spurpolynomen der linken und rechten Fahrbahnmarkierungen berechnet. Die Mittellinie der Fahrspur wird als Mittelwert der Positionen der linken und rechten Fahrbahnmarkierungen bestimmt und anschließend durch ein Polynom approximiert, das geglättet wird, um eine stabile Querregelung zu ermöglichen.
PAP
| Programmablaufplan |
 |
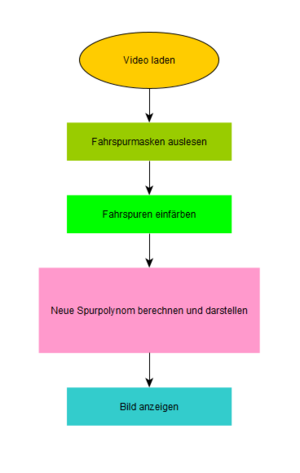Quelltext
| Quelltext 1: zeigeSpurpolynom.m |
%****************************************************************
% Hochschule Hamm-Lippstadt *
%****************************************************************
% Modul : SDE-Praktikum *
% *
% Datum : 20.06.2024 *
% *
% Funktion : zeigeSpurpolynom *
% *
% Implementation : MATLAB 2024a *
% *
% Req. Toolbox : - *
% *
% Author : Yuhan Pan,Xiangyao Liu,Yuhnkai Lin *
% *
% Bemerkung : *
% *
% Letzte Änderung : 03.07.2024 *
% *
%***************************************************************/
%% MATLAB initialisieren
clear all; close all
% cell-array mit Fahrbahnmarkierungen laden
load('GeradeInKurve_Segmente.mat')
[~,nMaxBilder]=size(Fahrbahnmarkierung)
%% Video laden
stDateiname = 'GeradeInKurve_IPT.mp4';
hVideo = VideoReader(stDateiname);
for nBild=1:nMaxBilder % Schleife über alle Frames
aFrame = readFrame(hVideo); % Bild laden
%% Fahrspurmasken auslesen
Fahrbahn=Fahrbahnmarkierung{nBild};
aLinkeFahrspur = Fahrbahn(:,:,1);
aMittelFahrspur = Fahrbahn(:,:,2);
aRechteFahrspur = Fahrbahn(:,:,3);
%% Fahrspuren einf?rben
% Farbkan?le trennen
R = aFrame(:,:,1);
G = aFrame(:,:,2);
B = aFrame(:,:,3);
% Grün
R(aLinkeFahrspur) = 0;
B(aLinkeFahrspur) = 0;
% Rot
G(aMittelFahrspur) = 0;
B(aMittelFahrspur) = 0;
% Gelb
B(aRechteFahrspur) = 0;
aRGBBild = cat(3, R, G, B); % Bild zusammenfassungen
%% Spurpolynom zwischen roten und gelben Fahrspuren berechnen und darstellen
[yMittel, xMittel] = find(aMittelFahrspur);
[yRechts, xRechts] = find(aRechteFahrspur);
if ~isempty(yMittel) && ~isempty(yRechts)
% Mittlere y-Koordinate als gemeinsame Basis verwenden
yGemeinsam = unique([yMittel; yRechts]);
% Polynom zwischen mittleren und rechten Fahrspuren anpassen
pMittel = polyfit(yMittel, xMittel, 2);
pRechts = polyfit(yRechts, xRechts, 2);
xMittelPoly = polyval(pMittel, yGemeinsam);
xRechtsPoly = polyval(pRechts, yGemeinsam);
% Mittelwert der x-Koordinaten als Spurpolynom berechnen
xSpurneu = (xMittelPoly + xRechtsPoly) / 2;
end
%% Bild anzeigen
imshow(aRGBBild)
title(['Frame: ', num2str(nBild), ' / ', num2str(nMaxBilder)]);
hold on;
if exist('xSpurneu','var')
h3 = plot(xSpurneu,yGemeinsam, 'w-', 'Linewidth', 2);
end
%% Legend hinzufuegen
h1 = plot(NaN, NaN, 'r-', 'LineWidth', 2); % Dummy plot for red legend
h2 = plot(NaN, NaN, 'y-', 'LineWidth', 2); % Dummy plot for yellow legend
legend([h1 h2 h3], {'Mittelspur', 'Rechtspur', 'Neuespur'});
hold off;
pause(0.01); % Kurze Pause, um das Bild anzuzeigen
end
|
Ergebnisse
Link zu den Video:
https://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/_Semesterordner/Team_3_Liu_Pan_Lin\Termin_9\Aufgabe_6.
-
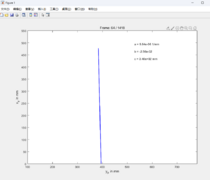
Abb. 2: Darstellung der Spurpolynome bei Gerade
-
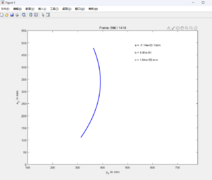
Abb. 3: Darstellung der Spurpolynome bei Linkskurve
-
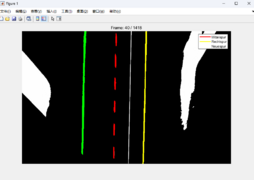
Abb. 4: zeigeSpurpolynom un Segmentierung in Gerade
-
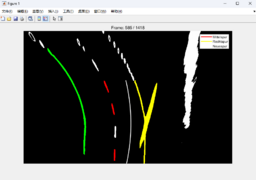
Abb. 5: zeigeSpurpolynom un Segmentierung in Linkskurve
Analyse
| Beschreibung | Das Problem ist.. | Das Problem ist nicht... |
|---|---|---|
| Was genau ist das Problem? | Bei Zeige der metrischen Spurpolynom in Fahrzeugkoordinaten werden den Einheit von Pixel in tatsächliche Länge nicht gut umwandeln | Zusätzliche Kannten werden nicht in Bilden anzeigen |
| Wo tritt das Problem auf? | Im der Video der metrischen Spurpolynom | Kamera und Video der Spurpolynom zu segmentieren |
| Wie zeigt sich das Problem? | Spurparameter a, b und c sind anormal | bei der Fahrzeugkoordinaten sind die Wert zu groß, und Der Ursprungpunkt der Koordinaten stimmt nicht mit dem Wagen überein. |
| Wann tritt das Problem auf? | Bei den metrischen Polynom zu polten | |
| Warum ist es ein Problem? | Verwirrende Einheiten können nicht verwendet werden, um den Querregelung zu funktionieren und soll Bahn des Autos festzulegen |
| Beschreibung | Das Problem ist.. | Das Problem ist nicht... |
|---|---|---|
| Was genau ist das Problem? | Bei Linkskurve ist den Spurpolynom bei Zeige der Segmente nicht stabil | |
| Wo tritt das Problem auf? | Der Anbiegen des Autos | Geradefahren |
| Wie zeigt sich das Problem? | erkennt Hindernisse am Straßenrand als Spuren | |
| Wann tritt das Problem auf? | Fahren bei Linkskurve, besonders am die Ende | Geradefahren |
| Warum ist es ein Problem? | Misserkannt der Spur kann zum Abdriftung des Fahrzeuges von der Fahrspur |
| Nr. | Beschreibung |
|---|---|
| 1 | Bei Läuf der Programm ist der Umwandlung der Einheit falsch |
| 2 | Zusätzliche Kanten und Muster sind gerade weiß und schwarz, das ist einfach zu erkennen. |
| Nr. | Maßnahme | Verantwortung | Termin | Status |
|---|---|---|---|---|
| 1 | Im Skript der metrischen Spurpolynom den Einheit von Koordinate umberechnen | Liu Pan Lin | 04.07.2024 |  |
| 2 | Im Skript der metrischen Spurpolynom den Einheit von Spurparametern umberechnen | Liu Pan Lin | 04.07.2024 | |
| 3 | Visuelle Überprüfung durch Einblendung in das Ergebnisvideo | Liu Pan Lin | 04.07.2024 |  |
Hinweis: Die Maßnahmen müssen nicht umgesetzt werden.
Zusammenfassung
- Zusammenfassung
Diese Aufgabe wird durch die Extraktion von Fahrspurmarkierungen und die Berechnung und Visualisierung der Fahrspurlinien zwischen der mittleren und der rechten Fahrspur auf der Grundlage einer polynomialen Interpolation erfüllt.
- Diskussion der Ergebnisse
Eine glatte und genaue Fahrbahnmodellierung kann durch polynomiale Interpolation erreicht werden.
- Ausblick
Optimierung des Algorithmus für Echtzeit-Verarbeitung, um ihn in realen Fahrzeugen einsetzen zu können.
- Lessons Learned
Die polynomiale Interpolation erweist sich als wirksame Methode zur Modellierung von Fahrspuren, insbesondere bei Verwendung einheitlicher y-Koordinaten.
Beantwortung der Lernzielkontrollfragen
Wie lassen sich die Spurpolynome für die 3 Segmente bestimmen?
Die Spurpolynome werden durch Extrahieren der Fahrspurpunkte und Anwenden der Methode der kleinsten Quadrate bestimmt.
Welche Vor- und Nachteile hat die Polynombildung?
Vorteile:
Einfache Implementierung
Flexibilität bei Kurvenformen
Es ist möglich, die Krümmung des Spur zu visualisieren, um Querreglung zu funktionieren. Dadurch kann es dazu führen, welche Bahn das Auto fahren würde (Istgröße) und welche Bahn das Auto fahren soll (Sollgröße)
Nachteile:
Oszillationen bei höhergradigen Polynomen
Überanpassung
Numerische Instabilität
Wie könnten die Nachteile behandelt werden?
Verwendung niedrigerer Polynome
Einsatz von Spline-Interpolation
Anwendung von Glättungstechniken
Wie lauten die Umrechnungsfaktoren Pixel in m in xF- und yF-Richtung?
xF-Richtung: (2 * (Kamerahöhe + Abstand zur Fahrzeugfront) * tan(Kameraneigung)) / Bildhöhe in Pixel
yF-Richtung: Fahrzeugbreite / Bildbreite in Pixel
Wie wird der Blindbereich vorm Fahrzeug berücksichtigt?
Nur die sichtbaren Bereiche des Bildes werden transformiert und weiterverarbeitet.
Wie wird das Spurpolynom für die Querregelung aus den Spurpolynomen der Fahrbahnmarkierungen ermittelt?
Die Mittellinie wird als Mittelwert der Positionen der linken und rechten Fahrbahnmarkierungen bestimmt und durch ein Polynom approximiert.
→ zurück zum Hauptartikel: Praktikum SDE | SDE-Team 2024/25 | Lernzielkontrolle 3