Montage der Legosteine mit dem UR3-Roboter

→ zurück zum Hauptartikel: Automatische Legostein-Montieranlage

Autoren: Alexander Rips und Tim Kolem

In diesem Kapitel wird erklärt, wie mit dem UR3 Greifarmroboter und mithilfe eines geeigneten Programms Legosteine montiert werden können.

UR3 Greifarmroboter zu Beginn des Praktikums

Unser Hauptprogramm ist aufgeteilt in 3 Unterprogramme, die gleichzeitig ausgeführt werden. Diese Unterprogramme sind die Längsregelung, die Querregelung und die Ausführung der Kamera.

Einleitung

Dies ist der Wiki Artikel zur Dokumentation der Arbeitsergebnisse der Gruppe "Montage der Legosteine mit dem UR3-Roboter" des Projekts, welches im Praktikum der Produktionstechnik Automatische_Legostein-Montieranlage absolviert worden ist. Innerhalb dieses Artikels wird erläutert, wie der UR3 Roboter mithilfe von MATLAB angesteuert werden kann, und wie die Koordinaten der zu platzierenden Legosteine errechnet werden können.

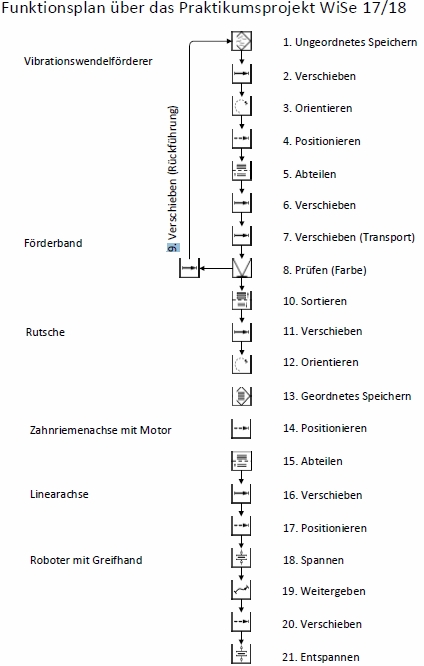
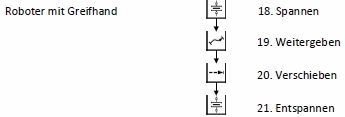
In dem Funktionsplan der Aufgabenstellung übernimmt der Roboter die Teilaufgaben 18 bis 21.

Er soll den Legostein von dem Block auf der Linearachse aufnehmen, ihn auf seiner Zielposition platzieren und loslassen. Die genauen Arbeitsschritte des Roboters werden im folgenden Abschnitt des Funktionsplans dargestellt:

Inhalt

Programmablauf

Für den Programmablauf gibt es das Problem, dass es als Vorschaubild die maximale Größe überschreitet und nicht dargestellt wird. In dem Kapitel "Originaldateien" ist der Programmablaufplan (v3) in voller Auflösung zu finden.

Originaldateien

Als erstes muss die Verbindung über TCP/IP hergestellt werden. Wenn die Verbindungsherstellung fehlerfrei erfolgt ist, werden die Koordinaten der einzelnen Legonoppen aus der Excel-Datei in Form einer Listenstruktur gespeichert. Im nächsten Schritt werden aus den Koordinaten, welche in Legonoppen vorliegen, die realen Koordinaten ausgehend von der linken unteren Ecke der Legoplatte berechnet. Anschließend muss eine zweite Transformation der Koordinaten durchgeführt werden, mit welcher die Koordinaten auf der Legoplatte zu Koordinaten des Roboters umgerechnet werden.

Nachdem alle Koordinaten transformiert sind, müssen die einzelnen Steine gesetzt werden. Der nächste zu setzende Stein muss über ein Signal an der SPS angefordert werden. Sobald die SPS dem Roboter über ein Signal mitgeteilt hat, dass ein neuer Stein verfügbar ist, muss der Roboter den Stein greifen und an seiner Zielposition platzieren. Dabei sollten zwei Dinge beachtet werden: Die gewünschte "Pose" (Rx,Ry,Rz), mit welcher der Roboter den Stein platzieren soll, muss im Vorfeld vom Terminal des Roboters abgelesen werden. Zusätzlich sollte beachtet werden, dass der Roboter einzelne Positionen nur von oben anfahren kann. Genauere Details befinden sich im Programmablaufplan.

UR3 Greifarmroboter

Gute Literatur findet sich unter: UR3 User Manual En UR3 Service Manual En Script Programming Language En .

Teilweise gibt es auch in deutsche übersetzte Versionen, aber diese waren nicht immer eindeutig erklärt. Die englischen Skripte sind gut zu verstehen. Kurz zur Semantik in diesem Abschnitt. Der Endeffektor des 6 Achsgreifarmroboters ist das letzte, also äußerste Glied. Mit "Werkzeug" wird der Greifer gemeint. Für die Beschreibung der Bewegungen ist der Unterschied irrelevant.

Der UR3 besitzt 6 Achsen und hat vorne am Werkzeugende einen RG2 Gripper montiert, mit welchem die Legosteine gegriffen werden können müssen.

Er arbeitet mit einem 500 mm Arbeitsradius und einer maximalen Nutzlast von 3 kg. Bewegungen nah am Fuß des Roboters sollten vermieden werden, da selbst kleine Bewegungen des Werkzeugs große Bewegungen in den Achsen verursachen können und so den Sicherheitsstopp auslösen.

Gesteuert werden kann dieser unter anderem direkt von dem Control Panel, dem Tablet, aus, welches am Tisch montiert ist. Es wird ein neues Programm gestartet und dort unter dem Reiter "Struktur" Bewegungen / Wegpunkte hinzugefügt. Unter "URCaps" kann der Greifer bedient werden. Unter dem Reiter "Bewegung" kann die aktuelle Position und Pose des UR3 abgelesen werden. Beachte: Auf der rechten Seite die tabellarischen Gelenkkoordinaten auf "Fuß" stellen.

Zur Bewegung gibt es drei wesentlich interessante Bewegungen: MoveL, MoveJ und MoveP. Hierfür wird die PDF Script Programming Language En, S. 14f empfohlen.

An dieser Stelle eine kurze Übersicht:

MoveL steht für eine lineare Bewegung.

• Bei diesem Befehl werden komplexe Gelenkbewegungen berechnet, damit das Werkzeug eine lineare Bewegung zwischen zwei Wegpunkten erfährt.
• Gemeinsame Parameter sind die maximale Gelenkgeschwindigkeit und Gelenkbeschleunigung [m/s und m/s²] (in Polyscope (Betriebssystem des Tablet) mit den Einheiten mm/s und mm/s²)
• Übergeben wird die Pose in [x, y, z, rx, ry, rz] (x, y, z: Raumkoordinaten und rx, ry, rz: die Pose/ "Stellung" des Endeffektors)

MoveJ steht für eine Gelenk (Joint) Bewegung.

• Bei diesem Befehl werden alle Gelenke die gewünschte Stellung gleichzeitig erreichen, wodurch das Werkzeug eine gekrümmte Bewegung erfährt.
• Gemeinsame Parameter sind hier die maximale Gelenkgeschwindigkeit und Gelenkbeschleunigung [deg/s und deg/s²], Gelenkposition (Pose), Zeit und Radius
• Geeignet ist diese Bewegungsart für schnelle Bewegungen des Roboters ungeachtet der Bewegung des Werkzeuges. Etwa um in die Ausgangsposition zu fahren. (Auf Kollisionsfreiheit achten!)

MoveP steht für eine Bewegung mit Pose.

• Bei diesem Befehl wird das Werkzeug linear bei konstanter Geschwindigkeit und kreisrunden Biegungen bewegt.
• Der Kurvenradius ist ein gemeinsamer Mittelwert aller Wegpunkte. Der Roboterarm fährt mit konstanter Geschwindigkeit durch alle Wegpunkte. Währenddessen kann das Robotersteuergerät weder durch E/A noch durch die Benutzereingabe bedient werden. Der Versuch kann den Schutz-Aus auslösen oder die Bewegung stoppen.
• Hier sind die Parameter Pose, Gelenkbeschleunigung, Gelenkgeschwindigkeit und der Kurvenradius.
• Geeignet ist diese Bewegung für beispielsweise Klebevorgänge oder zum Ausgeben.

RG2 Gripper

Gute Literatur findet sich unter: RG2 User Manual En .

Der Greifer ist bereits montiert und hat einen Klemmschutz installiert. Beim Bedienen des Grippers gilt es gewisse Punkte zu beachten, die direkt auf dem Tablet eingestellt werden:

1. unter "Installation" - "RG2 Configuration" - "Settings" den Fingertip Offset richtig einstellen!
2. unter "Installation" - "RG2 Configuration" - "Mounting" die richtige Ausrichtung überprüfen.

Dem Skript können die Dimensionen des Greifers entnommen werden und anhand dieser neue Fingertips in SolidWorks entworfen werden. Dies ist notwendig, da die mitgelieferten Fingertips die Legosteine weder gut greifen, noch gut platzieren können.

Beim Entwerfen der Fingertips muss darauf geachtet werden, dass der Legostein gut platziert werden kann und der Legostein vorzugsweise in einer einzigen möglichen definierten Position zwischen den beiden Fingertips liegt.

Das Problem dabei ist, dass beim eindeutigen Greifen der Legosteine dieser umschlossen wird von den Fingertips und dadurch zu allen Seiten hin etwas Abstand braucht und somit nicht an anliegende Steine angebaut werden kann. Es müssen also 2 verschiedene Fingertips entworfen werden. Mit den einen kann eine genaue Legosteinaufnahme durchgeführt werden, mit den anderen Fingertips können die Steine platziert werden, auch an anliegende andere Steine. Die Abbildungen in diesem Abschnitt zeigen Beispiele für Fingertips zum Kalibrieren und Platzieren. Eventuell ist es notwendig auch auf die Fingertips zum Kalibrieren Aufdrückflächen anzubringen.

• 

  Bsp Fingertip für den RG2 zum Kalibrieren

• 

  Bsp für den RG2 zum Kalibrieren komplett mit Legostein

• 

  Bsp für den RG2 zum Platzieren mit Andrückfläche

Alle Dateien können im SVN gefunden oder bei den Autoren erfragt werden.

SPS Schnittstelle

Gute Literatur findet sich unter: Schnelleinstieg --> downloads oder alternativ nach einem Schnelleinstieg für "axc 1050 pn starter kit" suchen.

und UR3 Service Manual En

Die SPS soll eine Kommunikation mit den anderen Gruppen ermöglichen. Hierfür werden 4 Ein- und Ausgänge gebraucht.

1. Eingang teilt mit, welche Farbe angekommen ist
2. Eingang teilt mit, welche Farbe angekommen ist
3. Eingang teilt mit, welche Farbe angekommen ist
4. Eingang gibt ein Signal, wenn ein Stein bereit zur Aufnahme ist.

Für die Ausgänge läuft es ähnlich ab.

1. Ausgang gibt an, welche Farbe benötigt wird
2. Ausgang gibt an, welche Farbe benötigt wird
3. Ausgang gibt an, welche Farbe benötigt wird
4. Ausgang gibt ein Signal, wenn der Greifer bereit zur Aufnahme ist.

In dem UR3 Service Manual steht unter Punkt 4.3 Steuergerät E/A die Bedeutung der verschiedenen Farben der SPS.

Gelbe Klemmen: Konfigurierbare E/A (sicherheits-relevanter E/A oder allgemeiner E/A)

Graue Klemmen: digitale E/A für allgemeine Zwecke

Grüne Klemmen: Spannung (0-10 V)oder Strom (4-20 mA) von und zu anderen Geräten messen

Die Stromversorgung ist standardmäßig intern und sollte so belassen werden.

Ansteuerung des Roboters mithilfe von MATLAB

Innerhalb dieses Unterabschnittes wird erläutert, wie der UR3-Roboter über MATLAB angesteuert werden kann. Die Ansteuerung des UR3 Greifarmroboters erfolgt über das TCP/IP-Protokoll mithilfe der "tcpip"-Klasse der MATLAB-Standardbibliothek. Es muss beachtet werden, dass der verwendete Computer mit einem Ethernet-Kabel mit dem UR3-Greifarmroboter verbunden werden muss und MATLAB einen Zugriff auf das Netzwerk erhalten muss. Im Falle von Windows 10 können die Netzwerkeinstellungen der einzelnen Anwendungen unter (Systemsteuerung -> System und Sicherheit -> Windows Defender Firewall -> Zugelassene Apps) festgelegt werden. Für diese Operation werden Administratorrechte benötigt. Wenn nun der Roboter mit einem Ethernet-Kabel mit dem Computer verbunden wurde und die Firewall korrekt konfiguriert worden ist, kann eine TCP/IP-Verbindung mit folgender Programmzeile hergestellt werden: "Socket_conn = tcpip(Robot_IP,Port_NR);". Dabei ist "Robot_IP" die IP-Adresse des Roboters, welche in Form eines Strings an diese Funktion übergeben wird. Zum aktuellen Zeitpunkt hat der Roboter die IP-Adresse 192.168.0.2. Mit der Variablen "Port_NR" wird die Portnummer angegeben, welche angesprochen werden soll. Für den UR3-Roboter muss die Portnummer 30003 gewählt werden.

Nachdem die Verbindung erfolgreich hergestellt worden ist, können Befehle über die TCP/IP-Verbindung an den Roboter gesendet werden. Dies geschieht wie folgt mit dem Aufruf der "fprintf"-Funktion:

"fprintf(Socket_conn, Befehl);"

Dabei ist "Socket_conn" das zuvor beim Verbindungsaufbau definierte Socket-Objekt der hergestellten Verbindung und "Befehl" ein String, welcher an den Roboter übertragen werden soll.

In dem Scriptmanual werden alle Befehle aufgelistet, welche der Roboter verarbeiten kann. Von besonderem Interesse für dieses Projekt sind die "move" Befehle ab Seite 13.

Umrechnung der logischen Koordinaten in Koordinaten des Roboters

In diesem Unterabschnitt wird thematisiert wie die Koordinaten, welche in der Excel Tabelle hinterlegt werden, zu den realen Koordinaten des Roboters umgerechnet werden können. Dabei erfolgen genau genommen zwei einzelne Transformationen. Zum einen eine Transformation von den in der Excel-Tabelle angegebenen Koordinaten in Legonoppen zu den realen Koordinaten des "Legoplattensystems". Und zum Anderen eine Transformation der Koordinaten des "Legoplattensystems" in das Koordinatensystem des Roboters.

Auslesen der Excel Tabelle

Zunächst einmal muss die hinterlegte Excel-Tabelle ausgelesen werden. Dieser Auslesevorgang wird mithilfe der Funktion "xlsread" der MATLAB-Standardbibliothek realisiert. Der genaue Befehl zum Auslesen der xlsx-Datei lautet wie folgt: "xlsread('Robokoords.xlsx',,,'basic');". Dabei ist "Robokoords.xlsx" der Name der hinterlegten xlsx-Tabelle. Der Rückgabewert dieser Funktion ist bei einer fehlerfreien Ausführung der Funktion, eine Matrix mit den Tabelleninhalten der mit "Robokoords.xlsx" spezifizierten Excel-Tabelle. Eine genauere Dokumentation des "xlsread"-Befehls befindet sich in der MATLAB-Dokumentation unter Mathworks . Nachdem die Excel-Tabelle in eine Matrix geladen worden ist, kann durch diese zeilenweise iteriert werden, da jeder zu platzierende Stein eine Zeile in der Tabelle repräsentiert.

Errechnung der realen Koordinaten auf der Legoplatte

Die Koordinaten der einzelnen Legosteine innerhalb der Excel-Tabelle werden in "Legonoppen" ausgehend von der linken unteren Ecke referenziert. Dies bedeutet das ein Stein mit den Koordinaten (0;0) mit seiner linken unteren Noppe auf der ersten Noppe links unten auf der Legoplatte platziert werden soll. Ein Stein mit den Koordinaten (1;0) wird mit seiner unteren linken Noppe eine Noppe weiter rechts von dem (0;0) Stein platziert. Der Stein mit den Koordinaten (0;1) wir eine Noppe über dem (0;0)-Stein platziert.

Die realen Koordinaten bezeichnen den Punkt im Raum, den der TCP des UR3-Roboters einnehmen muss, um den Legostein zu platzieren. Selbstverständlich müssen diese Koordinaten später von oben angefahren werden.

Die Koordinaten auf der Legoplatte werden wie folgt berechnet:

$Koordinate \, Legoplatte = Anzahl\,der\,Noppen \cdot Abstand\,zweier\,Noppen + Halbe\,Laenge\,des\,Steins$

Dies gilt analog für die x-Koordinate und die y-Koordinate.

Es muss zusätzlich noch ein Noppenabstand von der x-Koordinate als auch von der y-Koordinate abgezogen werden. Der Grund für diese Subtraktion ist darin begründet, dass nur Punkte innerhalb eines 2x2 Noppenfeldes exakt mit dem Roboter ermittelt werden können und bei der Kalibrierung unter anderem dieser Punkt aufgenommen werden soll. Folgende Abbildung verdeutlicht diesen Sachverhalt:

Berechnung der Roboterkoordinaten mithilfe der Legoplattenkoordinaten

In diesem Unterabschnitt wird erläutert, wie die Koordinaten der Legoplatte zu Koordinaten des Roboterkoordinatensystems umgerechnet werden können.

Der Vektor von dem Nullpunkt des Legoplatten-Koordinatensystems zum gesuchten Punkt ist aus dem vorherigen Schritt bekannt. Gesucht ist nun der Vektor vom Nullpunkt des Roboterkoordinatensystems zum gesuchten Punkt. Innerhalb dieses Abschnitts wird erläutert, wie eine Transformationsmatrix errechnet werden kann, mit welcher der gegebene Vektor des Legoplattenkoordinatensystems in das Roboterkoordinatensystems transformiert. Um die Koordinaten zu transformieren wird die homogene Transformation angewendet.

Dieser Vorgang wird in folgender Abbildung exemplarisch dargestellt:

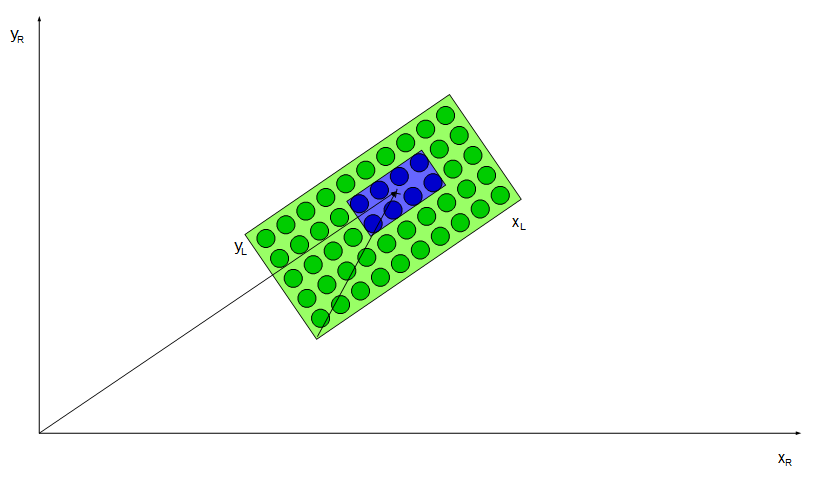
Eingezeichnet ist das Koordinatensystem des Roboters. Der Nullpunkt vom Legoplattenkoordinatensystem befindet sich auf der unteren linken Ecke der Legoplatte.

Damit die Tranformation durchgeführt werden kann, muss zunächst einmal die Transformationsmatrix ermittelt werden. Vereinfachend wird angenommen, dass nur eine Drehung um die z-Achse durchgeführt wird. Die folgende Matrix ist die Transformationsmatrix einer homogenen Transformation im dreidimensionalen Raum.

$\begin{pmatrix} cos(a) & -sin(a) & 0 & tx\\ sin(a) & cos(a) & 0 & ty\\ 0 & 0 & 1 & tz\\ 0 & 0 & 0 & 1 \\ \end{pmatrix}$

An dieser Stelle sei auch erwähnt, dass sich die gesamte homogene Transformation wie folgt ergibt:

$\begin{pmatrix} cos(a) & -sin(a) & 0 & tx\\ sin(a) & cos(a) & 0 & ty\\ 0 & 0 & 1 & tz\\ 0 & 0 & 0 & 1 \\ \end{pmatrix} \cdot \begin{pmatrix} x_{untransformiert}\\ y_{untransformiert}\\ z_{untransformiert}\\ 1\\ \end{pmatrix} = \begin{pmatrix} x_{transformiert}\\ y_{transformiert}\\ z_{transformiert}\\ 1\\ \end{pmatrix}$

Diese Matrix enthält vier unbekannte Variablen, demzufolge werden auch vier Gleichungen benötigt um diese Matrix ermitteln zu können.

Diese Matrix kann durch das Lösen eines linearen Gleichungssystems bestimmt werden. Hierfür müssen mindestens zwei Punkte aufgenommen werden. Zur Kalibrierung wird der Stein im Greifer des UR3-Roboters platziert und dieser so auf die Legoplatte geführt, dass sich der Stein an der gewünschten Position befindet. Anschließend können die Koordinaten von der Polyscope Oberfläche des UR3-Benutzerterminals abgelesen werden.

WICHTIG: Im Vorfeld muss das Terminal auf das richtige Koordinatensystem konfiguriert werden. Dieses muss von "Ansicht" auf "Fuß" gestellt werden. Andernfalls werden nicht die gewünschten Koordinaten angezeigt.

Um den Roboter zu kalibrieren müssen zwei Punkte des Legofeldes "eingeteacht" werden. Es bietet sich an, einen Stein so zu platzieren, dass sein Mittelpunkt im Mittelpunkt des 2x2 Feldes der unteren linken Ecke ist. In diesem Fall ist auch der Translationsvektor der homogenen Transformation bekannt. Um die Transformationsmatrix möglichst einfach bestimmen zu können, wird als zweiter einzulernender Punkt ein Punkt gewählt, welcher vom ersten aufgenommenen Punkt aus gesehen, eine feste Distanz nach rechts verschoben ist.

Das Gleichungssystem, mit welchem die Transformationsmatrix ermittelt werden kann kann mit diesen Informationen aufgestellt werden. Vom ersten Punkt, in der unteren linken Ecke ist bekannt, dass sich dieser im Ursprung des Legoplattenkoordinatensystems befindet. Dies bedeutet, dass dieser im Legoplattenkoordinatensystem die Koordinaten (0,0,0) besitzt. Somit kann das folgende lineare Gleichungssystem aufgestellt werden:

$T^{RL} \cdot PUL_{L} = PUL_{R}$

Dabei ist T Transformationsmatrix der homogenen Transformation, um die Koordinaten der Legoplatte in das Koordinatensystem des Roboters umzuwandeln. PUL_{L} ist der errechnete Punkt auf der Legoplatte und PUL_{R} ist der von dem Panel abgelesene reale Punkt des Roboterkoordinatensystems.

$\begin{pmatrix} cos(a) & -sin(a) & 0 & tx\\ sin(a) & cos(a) & 0 & ty\\ 0 & 0 & 1 & tz\\ 0 & 0 & 0 & 1 \\ \end{pmatrix} \cdot \begin{pmatrix} 0\\ 0\\ 0\\ 1\\ \end{pmatrix} = \begin{pmatrix} tx\\ ty\\ tz\\ 1\\ \end{pmatrix} = \begin{pmatrix} x_{Roboter unten links}\\ y_{Roboter unten links}\\ z_{Roboter unten links}\\ 1\\ \end{pmatrix}$

Wie in der Transformation zu erkennen ist, können alle drei Komponenten des Translationsvektors von der Polyscope-Benutzeroberfläche abgelesen werden. In dem Matlab Programm wird der Punkt im Ursprung des Legokoordinatensystems mit PUL (Punkt unten links) bezeichnet. Dieser Sachverhalt wird in folgender Abbindung verdeutlicht: Die untransformierten PUL Koordinaten kann errechnet werden, da die Anzahl der Noppen (in diesem Fall 0) in x- und y-Richtung bekannt sind. Der transformierte Punkt PUL kann von der Benutzeroberfläche des Roboters abgelesen werden, wenn dieser mit gegriffenem Stein auf die gewünschte Koordinate bewegt wird. Somit ist nur die Matrix unbekannt. Um die einzelnen Komponenten der Matrix vollständig bestimmen zu können wird ein zweiter abgelesener Punkt benötigt.

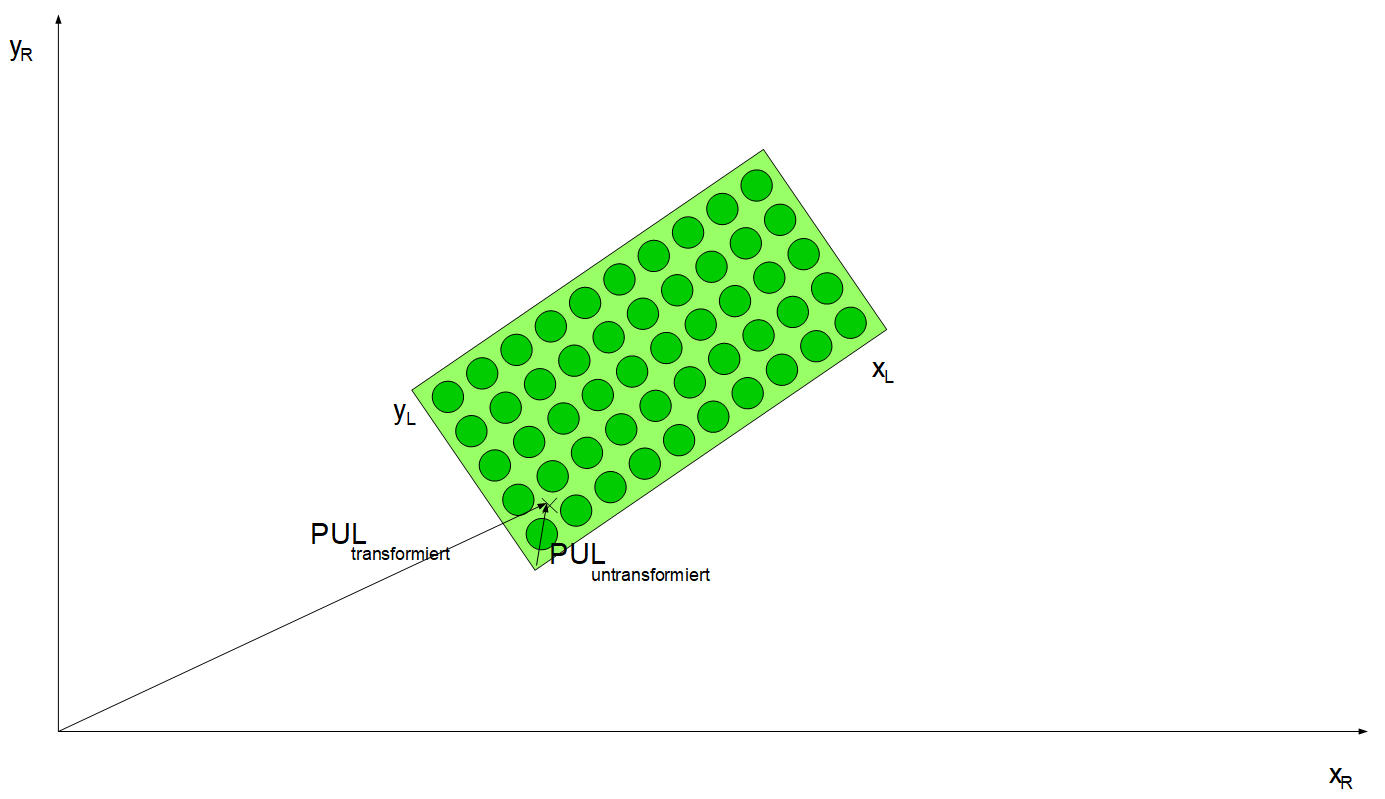
Nun muss eine weitere Koordinate eingelesen werden. Es bietet sich an, den Greifer mit dem gegriffenen Stein auf der Legoplatte nur in x-Richtung oder y-Richtung zu bewegen, da dies die Berechnung der fehlenden Komponenten der Transformationsmatrix erheblich vereinfacht. In dem folgenden Beispiel wird angenommen, dass der Roboterarm mit gefasstem Stein um 9 Noppen nach rechts bewegt worden ist, ausgehend von der Ecke unten links, an welcher die ersten Koordinaten abgelesen wurden. Folgendes Beispiel verdeutlicht diesen Sachverhalt, dabei sei l der Abstand zwischen zwei Legonoppen:

$T^{RL} \cdot PUR_{L} = PUR_{R}$

Auch hier wird ein Punkt rechnerisch bestimmt und anschließend vom Panel abgelesen um die Transformationsmatrix T zu bestimmen.

$\begin{pmatrix} cos(a) & -sin(a) & 0 & tx\\ sin(a) & cos(a) & 0 & ty\\ 0 & 0 & 1 & tz\\ 0 & 0 & 0 & 1 \\ \end{pmatrix} \cdot \begin{pmatrix} 9 \cdot l\\ 0\\ 0\\ 1\\ \end{pmatrix} = \begin{pmatrix} 9 \cdot l \cdot cos(a) + tx\\ 9 \cdot l \cdot sin(a) + ty\\ 0\\ 1\\ \end{pmatrix} = \begin{pmatrix} x_{Roboter unten rechts}\\ y_{Roboter unten rechts}\\ z_{Roboter unten rechts}\\ 1\\ \end{pmatrix}$

Derjenige Punkt, der sich um 9 Noppen versetzt vom Ursprung befindet, wird im Matlab-Programm mit PUR (Punkt unten rechts) bezeichnet. Die realen Koordinaten des Roboters können nun von dem Panel des Roboters abgelesen werden und im Matlab-Programm ergänzt werden.

Durch Termumformung können nun Formeln für cos(a) und sin(a) bestimmt werden. Dies geschieht wie folgt:

$x_{Roboter unten rechts} = 9 \cdot l \cdot cos(a) + tx$

$x_{Roboter unten rechts} - tx = 9 \cdot l \cdot cos(a)$

$\frac{x_{Roboter unten rechts} - tx}{9 \cdot l} = cos(a)$

Analog kann die Gleichung für sin(a) hergeleitet werden:

$y_{Roboter unten rechts} = 9 \cdot l \cdot sin(a) + ty$

$y_{Roboter unten rechts} - ty = 9 \cdot l \cdot sin(a)$

$\frac{y_{Roboter unten rechts} - ty}{9 \cdot l} = sin(a)$

Somit kann die Transformationsmatrix vollständig bestimmt werden und jeder beliebige Punkt der Legoplatte in das Koordinatensystem des Roboters transformiert werden. Folgende Abbildung verdeutlicht wie das Lineare Gleichungssystem anhand des zweiten Koordinatenpaares hergeleitet werden kann:

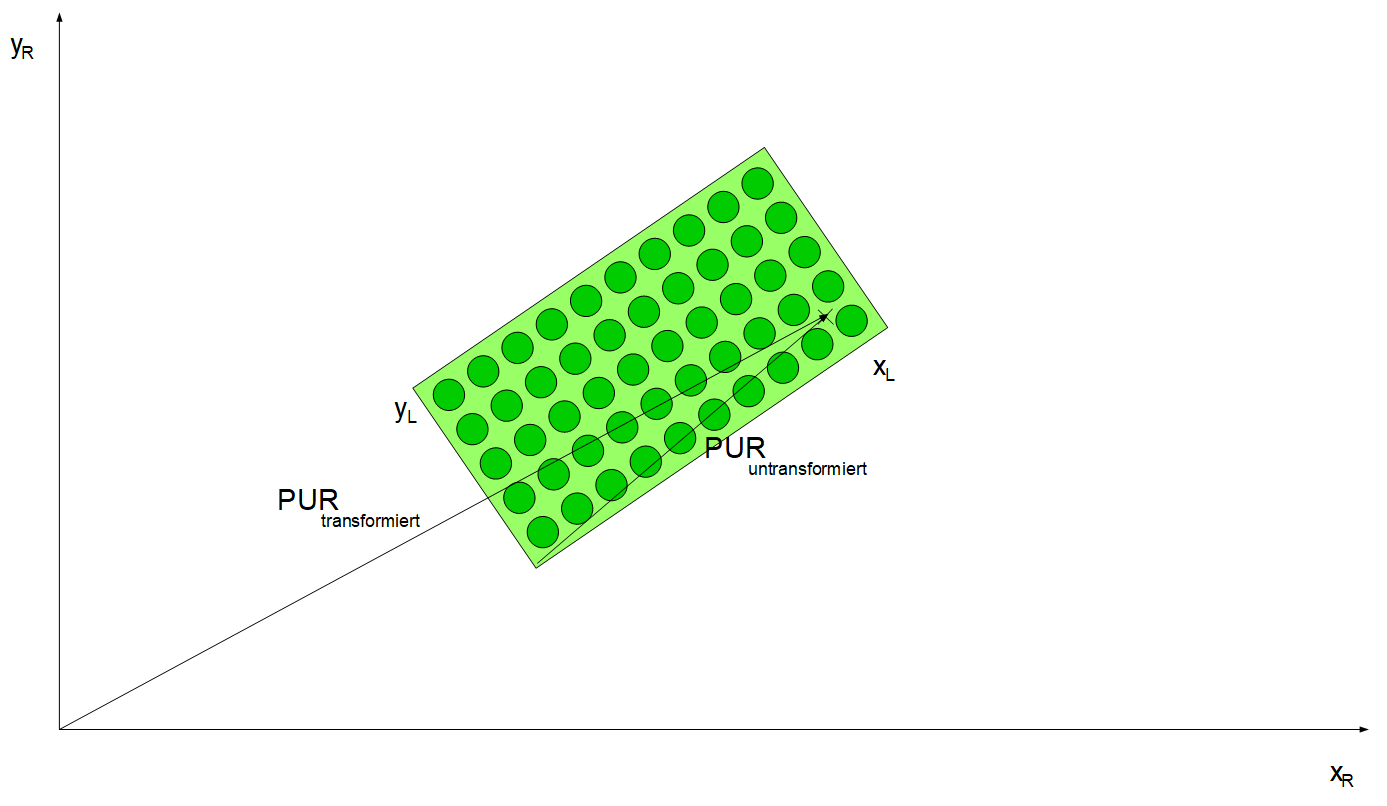
Alternativ kann die Transformationsmatrix auch mit anderen Punkten errechnet werden, die zwei aufgeführten linearen Gleichungssysteme sollen nur als Beispiel dienen. Es kann auch ohne Bedenken ein von 9 verschiedener Abstand gewählt werden, jedoch müssen die Gleichungen im Programm abgeändert werden.

Schnittstelle zur vorigen Gruppe (Legostein Aufnahme)

Damit der Roboter Legosteine greifen kann, ist es wichtig, dass diese am immer selben Aufnahmepunkt ankommen und innerhalb des Arbeitsradius des UR3 Greifers sind. Ferner sollte der Tisch, auf dem der UR3 montiert ist, fest mit der restlichen Anlage verbunden sein, um ein Verrutschen zu vermeiden.

Zusammenfassung

Zielvorstellung:

1. Legosteine aufnehmen und so präzise platzieren, dass damit gebaut werden kann.

Herausforderungen:

1. Eine saubere Kalibrierung für das Koordinatensystem ermöglichen (durch geeignete Fingertips)
2. Matrix Transformation / Umrechnung
3. Ansteuerung des Roboterarms mithilfe von Matlab
4. Kommunikation mit einer SPS

Zur Seite des Gesamtprojektes

Ausblick

Zum aktuellen Zeitpunkt arbeitet das Programm noch nicht genau genug, dies kann folgende Gründe haben:

• Die Kalibrierung ist nicht genau genug. Wenn der Roboter auf die Legoplatte kalibriert wird und sich der Stein nicht genau genug im Greifer befindet, kann die abgelesene Position des TCP´s variieren. Wenn eine Position mit großem Fehler ausgelesen wird, so wird auch die resultierende Transformationsmatrix fehlerhaft sein.

• Die homogene Transformation mit einem Drehwinkel ist nicht ausreichend genau genug.

Die Tischplatte ist genau genommen nicht parallel zu der Ebene, welche von der x- und y- Achse des Roboters aufgespannt wird. In der Realität müsste auch um die x- und die y-Achse gedreht werden. Die Transformation mit Drehung um alle drei Achsen ist mit großer Wahrscheinlichkeit genauer als die Transformation mit nur einer Drehung um die z-Achse.

Zudem muss die Anbindung an die SPS-Steuerung implementiert werden. Diese besteht aus zwei Bestandteilen:

• Zum einen muss die SPS mit dem Roboter verbunden werden. Dies beinhaltet die Verkabelung der Ein- und Ausgänge.

• Zum anderen muss eine Schnittstelle vom Roboter zum MATLAB-Programm erstellt werden. Zum momentanen Zeitpunkt ist es nur möglich Befehle vom Computer zum Roboter zu senden. Jedoch kann der Roboter keine Daten an den Computer senden. Dies ist jedoch zwingend erforderlich, weil die gesamte Logik auf dem MATLAB-Programm ablaufen soll und dieses mit der SPS kommunizieren muss.

Folglich ist es notwendig ein Programm für den Roboter zu erstellen, welches Anweisungen des MATLAB-Programms empfangen kann, diese verwertet und ausführt. Zusätzlich muss es die Zustände der SPS-Eingänge abfragen und dem MATLAB-Programm über TCP/IP senden, damit das MATLAB Programm entscheiden kann, welcher Stein als nächstes gesetzt werden soll.

Originaldateien

Folgende .zip Datei enthält

1. eine CAD Zeichnung eines 2x4 Legosteines, CAD Zeichnungen der beiden verschiedenen Fingertips, jeweils eine .STL datei für den 3D Drucker, jeweils eine Baugruppe mit den Fingertips inklusive Schiene.
2. alle verwendeten Matlab functions.
3. Roboter Excel für "createMovelCommand" (Matlab), RoboterKoordinaten (Excel).
4. Programmablaufplan.

Medium:UR3_Roboter_Ergebnisse.zip