SoSe24 - Praktikum Systementwurf - Spurpolynom

| Autoren: | Yuhan Pan, Xiangyao Liu, Yunkai Lin |
| Thema: | Spurpolynom |
| Workshoptermin 9: | 20.06.2024 |
| Lernzielkontrolle 3: | 04.07.2024 |
Einleitung
In diesem Workshop lernen Sie, wie Bilddaten von Fahrzeugkameras verarbeitet werden, um Fahrspuren zu erkennen und zu analysieren. Der Fokus liegt auf der Transformation von Bildkoordinaten in Fahrzeugkoordinaten und der Erstellung von Polynomen zur Darstellung der Fahrspur. Zudem wird die Berücksichtigung des Blindbereichs und die Ermittlung der Mittellinie für die Querregelung behandelt.
Spurpolynom
In diesem Abschnitt werden die grundlegenden Konzepte und Techniken zur Ermittlung von Spurpolynomen erläutert. Dies umfasst die Theorie der Polynombildung, die Transformation von Bild- zu Fahrzeugkoordinaten, die Berücksichtigung des Blindbereichs sowie die Ermittlung des Spurpolynoms für die Querregelung.
Beschreibung die Theorie der Polynombildung
Die Polynombildung ist ein Verfahren zur Annäherung oder Interpolation von Datenpunkten durch ein Polynom. Ein Polynom n-ten Grades hat die Form: Die Koeffizienten werden so bestimmt, dass die Summe der quadrierten Abweichungen minimiert wird (Methode der kleinsten Quadrate). Im diese Workshop wurden Spurpolynom in Form: zeigen. Man kann durch den Segmentierung der Spurpolynom von Video der Queranzahl x und y festlegen, und durch den Queranzahl y und x den Spurparameter a, b und c berechnen.
Beschreiben Sie die KOS-Trafo Bild- zu Fahrzeugkoordinaten
Die KOS-Transformation wandelt Bildkoordinaten (u, v) in Fahrzeugkoordinaten (X, Y, Z) um. Zuerst werden Bildkoordinaten in Kamerakoordinaten umgerechnet, dann werden diese in Fahrzeugkoordinaten transformiert unter Berücksichtigung der Kameraposition und -neigung.
Berücksichtigung des Blindbereichs
Der Blindbereich umfasst Bereiche, die von der Kamera nicht erfasst werden können. Um den Blindbereich zu berücksichtigen, werden nur sichtbare Bereiche des Bildes in die Fahrzeugkoordinaten transformiert und weiterverarbeitet, indem sie geometrisch berechnet und maskiert werden.
Wie wird das Spurpolynom für die Querregelung aus den Spurpolynomen der Fahrbahnmarkierungen ermittelt?
Das Spurpolynom für die Querregelung wird aus den Spurpolynomen der linken und rechten Fahrbahnmarkierungen berechnet. Die Mittellinie der Fahrspur wird als Mittelwert der Positionen der linken und rechten Fahrbahnmarkierungen bestimmt und anschließend durch ein Polynom approximiert, das geglättet wird, um eine stabile Querregelung zu ermöglichen.
PAP
PAP Ihrer Lösung
| Programmablaufplan |
| PAP Ihrer Lösung |
Quelltext
| zeigeSpurpolynom.m |
%****************************************************************
% Hochschule Hamm-Lippstadt *
%****************************************************************
% Modul : SDE-Praktikum *
% *
% Datum : 20.06.2024 *
% *
% Funktion : zeigeSpurpolynom *
% *
% Implementation : MATLAB 2024a *
% *
% Req. Toolbox : - *
% *
% Author : Yuhan Pan,Xiangyao Liu,Yuhnkai Lin *
% *
% Bemerkung : *
% *
% Letzte Änderung : 03.07.2024 *
% *
%***************************************************************/
%% MATLAB initialisieren
clc; clear all; close all;
%% Pfade einstellen und Parameter laden
addpath 'C:\Semesterordner\SS2024\Team_3_Liu_Pan_Lin\Termin_9\Aufgabe_6'
% Parameter einstellen
Kameraneigung = 10; % Kameraneigung, Einheit: Grad
Kamerahoehe = 27.5 / 100; % Kamerahöhe über Boden, Einheit: Meter
FahrzeugfrontKamera = 27 / 100; % Abstand von Fahrzeugfront bis Kamera, Einheit: Meter
Fahrzeugbreite = 20 / 100; % Fahrzeugbreite, Einheit: Meter
% Winkel in Radiant umrechnen
Kameraneigung_rad = deg2rad(Kameraneigung);
% Video und Auflösung laden
stDateiname = 'GeradeInKurve_IPT.mp4';
hVideo = VideoReader(stDateiname);
width = hVideo.Width;
height = hVideo.Height;
% Berechnung der tatsächlichen Entfernung pro Pixel
d_per_pixel = Fahrzeugbreite / width; % tatsächliche Entfernung pro Pixel, Einheit: Meter
% cell-array mit Fahrbahnmarkierungen laden
load('GeradeInKurve_Segmente.mat')
[~, nMaxBilder] = size(Fahrbahnmarkierung);
% Video-Schreibobjekt öffnen
outputVideo = VideoWriter('GeradeInKurve_Spurpolynom.mp4', 'MPEG-4');
open(outputVideo);
% Initialisierung der Matrix zur Speicherung der Polynomkoeffizienten
PolyCoeffsHistory = zeros(nMaxBilder, 3); % Angenommen, es gibt drei Koeffizienten für das quadratische Polynom
for nBild = 1:nMaxBilder % Schleife über alle Frames
aFrame = readFrame(hVideo); % Bild laden
%% Fahrspurmasken auslesen
Fahrbahn = Fahrbahnmarkierung{nBild};
aLinkeFahrspur = Fahrbahn(:,:,1);
aMittelFahrspur = Fahrbahn(:,:,2);
aRechteFahrspur = Fahrbahn(:,:,3);
%% Fahrspuren einfärben
% Farbkanäle trennen
R = aFrame(:,:,1);
G = aFrame(:,:,2);
B = aFrame(:,:,3);
% Grün
R(aLinkeFahrspur) = 0;
B(aLinkeFahrspur) = 0;
% Rot
G(aMittelFahrspur) = 0;
B(aMittelFahrspur) = 0;
% Gelb
B(aRechteFahrspur) = 0;
aRGBBild = cat(3, R, G, B); % Bild zusammenfügen
%% Fahrspuren in Vektoren kopieren
[yRechts, xRechts] = find(aRechteFahrspur);
[yMitte, xMitte] = find(aMittelFahrspur);
% Sicherstellen, dass die Stichprobenpunkte einzigartig sind
[yRechts, uniqueIdxRechts] = unique(yRechts);
xRechts = xRechts(uniqueIdxRechts);
[yMitte, uniqueIdxMitte] = unique(yMitte);
xMitte = xMitte(uniqueIdxMitte);
% Punkteanzahl ausgleichen
if length(xRechts) > 1 && length(xMitte) > 1
if length(xRechts) > length(xMitte)
xMitteInterp = interp1(yMitte, xMitte, yRechts, 'linear', 'extrap');
yMitteInterp = yRechts;
xRechtsInterp = xRechts;
yRechtsInterp = yRechts;
else
xRechtsInterp = interp1(yRechts, xRechts, yMitte, 'linear', 'extrap');
yRechtsInterp = yMitte;
xMitteInterp = xMitte;
yMitteInterp = yMitte;
end
% Berechnung der Mittellinie der rechten Fahrspur
xB = (xRechtsInterp + xMitteInterp) / 2;
yB = (yRechtsInterp + yMitteInterp) / 2;
% Umrechnung in Fahrzeugkoordinaten
xF = (xB - width / 2) * d_per_pixel; % Querkoordinate, Einheit: Meter
yF = (height - yB) * d_per_pixel; % Längskoordinate, Einheit: Meter
% Punkte in eine Matrix umwandeln
aWegpunkte = [xF'; yF'];
% Quadratische Polynominterpolation durchführen
PolynomKoeffizienten = interpoliereFahrspur(aWegpunkte, 2);
% Speicherung der aktuellen Polynomkoeffizienten
PolyCoeffsHistory(nBild, :) = PolynomKoeffizienten;
% Polynomkoeffizienten mit gleitendem Durchschnitt glätten
if nBild > 1
windowSize = 5; % Größe des gleitenden Durchschnittsfensters
for j = 1:3
startIdx = max(1, nBild - windowSize + 1);
PolyCoeffsHistory(nBild, j) = mean(PolyCoeffsHistory(startIdx:nBild, j));
end
end
%% Weiße Parabel zeichnen (Querregelung)
xVehicle = linspace(min(xF), max(xF), 100);
yFitQuer = polyval(PolyCoeffsHistory(nBild, :), xVehicle);
% Umrechnung der Fahrzeugkoordinaten in Bildkoordinaten
xVehicle_img = (xVehicle / d_per_pixel) + width / 2;
yFitQuer_img = height - (yFitQuer / d_per_pixel);
% Sicherstellen, dass die interpolierten Punkte im Bildbereich liegen
validIdxQuer = (yFitQuer_img >= 1) & (yFitQuer_img <= height);
for i = 1:length(xVehicle_img)
if validIdxQuer(i)
yCoord = round(yFitQuer_img(i)); % y-Wert in Bildkoordinaten umrechnen
if yCoord > 0 && yCoord <= height && round(xVehicle_img(i)) > 0 && round(xVehicle_img(i)) <= width
aRGBBild(yCoord, round(xVehicle_img(i)), 1) = 255; % R
aRGBBild(yCoord, round(xVehicle_img(i)), 2) = 255; % G
aRGBBild(yCoord, round(xVehicle_img(i)), 3) = 255; % B
end
end
end
end
% Ergebnis im Video speichern
writeVideo(outputVideo, aRGBBild);
end
% Video-Schreibobjekt schließen
close(outputVideo);
% Polynomkoeffizienten speichern
save('Spurpolynom.mat', 'PolyCoeffsHistory');
%% Hilfsfunktion
function PolynomKoeffizienten = interpoliereFahrspur(aWegpunkte, n)
% Berechnung der kleinsten Quadrate Lösung für die n-te Ordnung der Polynominterpolation
A = ones(size(aWegpunkte, 2), n + 1);
for k = 1:n
A(:, k) = aWegpunkte(1, :).^(n + 1 - k);
end
b = aWegpunkte(2, :)';
PolynomKoeffizienten = A \ b; % Kleinste Quadrate Lösung
end
|
Ergebnisse
Link zu den Video:
https://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/_Semesterordner/Team_3_Liu_Pan_Lin\Termin_9\Aufgabe_6.
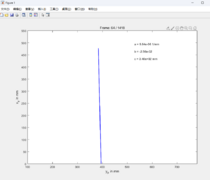
-
Abb. 2: Darstellung der Spurpolynome bei Gerade
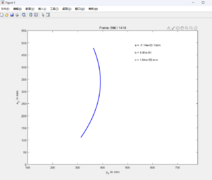
-
Abb. 3: Darstellung der Spurpolynome bei Linkskurve
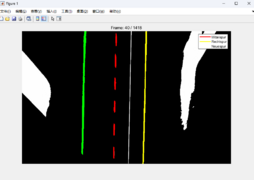
-
Abb. 4: zeigeSpurpolynom un Segmentierung in Gerade
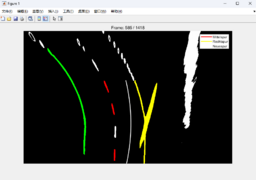
-
Abb. 5: zeigeSpurpolynom un Segmentierung in Linkskurve
Analyse
| Beschreibung | Das Problem ist.. | Das Problem ist nicht... |
|---|---|---|
| Was genau ist das Problem? | ||
| Wo tritt das Problem auf? | Beispiel | Beispiel |
| Wie zeigt sich das Problem? | Beispiel | Beispiel |
| Wann tritt das Problem auf? | Beispiel | Beispiel |
| Warum ist es ein Problem? | Beispiel | Beispiel |
| Nr. | Beschreibung |
|---|---|
| 1 | Warum? |
| Nr. | Maßnahme | Verantwortung | Termin | Status |
|---|---|---|---|---|
| 1 | Max Mustermann |
Hinweis: Die Maßnahmen müssen nicht umgesetzt werden.
Zusammenfassung
- Zusammenfassung
- Diskussion der Ergebnisse
- Ausblick
- Lessons Learned
Beantwortung der Lernzielkontrollfragen
Wie lassen sich die Spurpolynome für die 3 Segmente bestimmen?
Die Spurpolynome werden durch Extrahieren der Fahrspurpunkte und Anwenden der Methode der kleinsten Quadrate bestimmt.
Welche Vor- und Nachteile hat die Polynombildung?
Vorteile:
Einfache Implementierung
Flexibilität bei Kurvenformen
Nachteile:
Oszillationen bei höhergradigen Polynomen
Überanpassung
Numerische Instabilität
Wie könnten die Nachteile behandelt werden?
Verwendung niedrigerer Polynome
Einsatz von Spline-Interpolation
Anwendung von Glättungstechniken
Wie lauten die Umrechnungsfaktoren Pixel in m in xF- und yF-Richtung?
xF-Richtung: (2 * (Kamerahöhe + Abstand zur Fahrzeugfront) * tan(Kameraneigung)) / Bildhöhe in Pixel
yF-Richtung: Fahrzeugbreite / Bildbreite in Pixel
Wie wird der Blindbereich vorm Fahrzeug berücksichtigt?
Nur die sichtbaren Bereiche des Bildes werden transformiert und weiterverarbeitet.
Wie wird das Spurpolynom für die Querregelung aus den Spurpolynomen der Fahrbahnmarkierungen ermittelt?
Die Mittellinie wird als Mittelwert der Positionen der linken und rechten Fahrbahnmarkierungen bestimmt und durch ein Polynom approximiert.
→ zurück zum Hauptartikel: Praktikum SDE | SDE-Team 2024/25 | Lernzielkontrolle 3