%****************************************************************
% Hochschule Hamm-Lippstadt *
%****************************************************************
% Modul : SDE-Praktikum *
% *
% Datum : 20.06.2024 *
% *
% Funktion : zeigeSpurpolynom *
% *
% Implementation : MATLAB 2024a *
% *
% Req. Toolbox : - *
% *
% Author : Yuhan Pan,Xiangyao Liu,Yuhnkai Lin *
% *
% Bemerkung : *
% *
% Letzte Änderung : 03.07.2024 *
% *
%***************************************************************/
%% MATLAB initialisieren
clc; clear all; close all;
%% Pfade einstellen und Parameter laden
addpath 'C:\Semesterordner\SS2024\Team_3_Liu_Pan_Lin\Termin_9\Aufgabe_6'
% Parameter einstellen
Kameraneigung = 10; % Kameraneigung, Einheit: Grad
Kamerahoehe = 27.5 / 100; % Kamerahöhe über Boden, Einheit: Meter
FahrzeugfrontKamera = 27 / 100; % Abstand von Fahrzeugfront bis Kamera, Einheit: Meter
Fahrzeugbreite = 20 / 100; % Fahrzeugbreite, Einheit: Meter
% Winkel in Radiant umrechnen
Kameraneigung_rad = deg2rad(Kameraneigung);
% Video und Auflösung laden
stDateiname = 'GeradeInKurve_IPT.mp4';
hVideo = VideoReader(stDateiname);
width = hVideo.Width;
height = hVideo.Height;
% Berechnung der tatsächlichen Entfernung pro Pixel (angenommen, die Breite des Fahrzeugs wird von der Sichtweite der Kamera abgedeckt)
d_per_pixel = Fahrzeugbreite / width; % tatsächliche Entfernung pro Pixel, Einheit: Meter
% cell-array mit Fahrbahnmarkierungen laden
load('GeradeInKurve_Segmente.mat')
[~, nMaxBilder] = size(Fahrbahnmarkierung);
% Video-Schreibobjekt öffnen
outputVideo = VideoWriter('GeradeInKurve_Spurpolynom.mp4', 'MPEG-4');
open(outputVideo);
% Initialisierung der Matrix zur Speicherung der Polynomkoeffizienten
PolyCoeffsHistory = zeros(nMaxBilder, 3); % Angenommen, es gibt drei Koeffizienten für das quadratische Polynom
for nBild = 1:nMaxBilder % Schleife über alle Frames
aFrame = readFrame(hVideo); % Bild laden
%% Fahrspurmasken auslesen
Fahrbahn = Fahrbahnmarkierung{nBild};
aLinkeFahrspur = Fahrbahn(:,:,1);
aMittelFahrspur = Fahrbahn(:,:,2);
aRechteFahrspur = Fahrbahn(:,:,3);
%% Fahrspuren einfärben
% Farbkanäle trennen
R = aFrame(:,:,1);
G = aFrame(:,:,2);
B = aFrame(:,:,3);
% Grün
R(aLinkeFahrspur) = 0;
B(aLinkeFahrspur) = 0;
% Rot
G(aMittelFahrspur) = 0;
B(aMittelFahrspur) = 0;
% Gelb
B(aRechteFahrspur) = 0;
aRGBBild = cat(3, R, G, B); % Bild zusammenfügen
%% Fahrspuren in Vektoren kopieren
[yRechts, xRechts] = find(aRechteFahrspur);
[yMitte, xMitte] = find(aMittelFahrspur);
% Sicherstellen, dass die Stichprobenpunkte einzigartig sind
[yRechts, uniqueIdxRechts] = unique(yRechts);
xRechts = xRechts(uniqueIdxRechts);
[yMitte, uniqueIdxMitte] = unique(yMitte);
xMitte = xMitte(uniqueIdxMitte);
% Punkteanzahl ausgleichen
if length(xRechts) > 1 && length(xMitte) > 1
if length(xRechts) > length(xMitte)
xMitteInterp = interp1(yMitte, xMitte, yRechts, 'linear', 'extrap');
yMitteInterp = yRechts;
xRechtsInterp = xRechts;
yRechtsInterp = yRechts;
else
xRechtsInterp = interp1(yRechts, xRechts, yMitte, 'linear', 'extrap');
yRechtsInterp = yMitte;
xMitteInterp = xMitte;
yMitteInterp = yMitte;
end
% Berechnung der Mittellinie der rechten Fahrspur
xB = (xRechtsInterp + xMitteInterp) / 2;
yB = (yRechtsInterp + yMitteInterp) / 2;
% Umrechnung in Fahrzeugkoordinaten (angenommen, die Bildmitte ist der Ursprung des Fahrzeugkoordinatensystems)
xF = (xB - width / 2) * d_per_pixel; % Querkoordinate, Einheit: Meter
yF = (height - yB) * d_per_pixel; % Längskoordinate, Einheit: Meter
% Punkte in eine Matrix umwandeln
aWegpunkte = [xF'; yF'];
% Quadratische Polynominterpolation durchführen
PolynomKoeffizienten = interpoliereFahrspur(aWegpunkte, 2);
% Speicherung der aktuellen Polynomkoeffizienten
PolyCoeffsHistory(nBild, :) = PolynomKoeffizienten;
% Polynomkoeffizienten mit gleitendem Durchschnitt glätten
if nBild > 1
windowSize = 5; % Größe des gleitenden Durchschnittsfensters
for j = 1:3
startIdx = max(1, nBild - windowSize + 1);
PolyCoeffsHistory(nBild, j) = mean(PolyCoeffsHistory(startIdx:nBild, j));
end
end
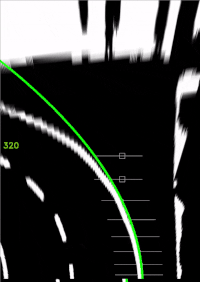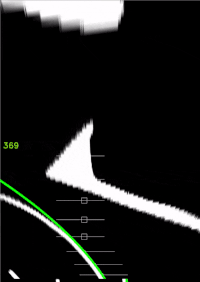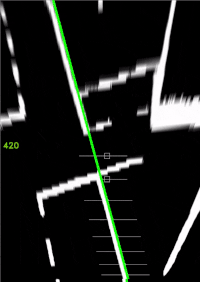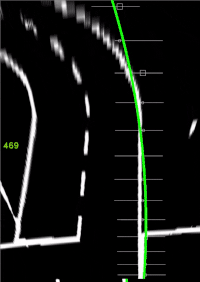
%% Weiße Parabel zeichnen (Querregelung)
xVehicle = linspace(min(xF), max(xF), 100);
yFitQuer = polyval(PolyCoeffsHistory(nBild, :), xVehicle);
% Umrechnung der Fahrzeugkoordinaten in Bildkoordinaten
xVehicle_img = (xVehicle / d_per_pixel) + width / 2;
yFitQuer_img = height - (yFitQuer / d_per_pixel);
% Sicherstellen, dass die interpolierten Punkte im Bildbereich liegen
validIdxQuer = (yFitQuer_img >= 1) & (yFitQuer_img <= height);
for i = 1:length(xVehicle_img)
if validIdxQuer(i)
yCoord = round(yFitQuer_img(i)); % y-Wert in Bildkoordinaten umrechnen
if yCoord > 0 && yCoord <= height && round(xVehicle_img(i)) > 0 && round(xVehicle_img(i)) <= width
aRGBBild(yCoord, round(xVehicle_img(i)), 1) = 255; % R
aRGBBild(yCoord, round(xVehicle_img(i)), 2) = 255; % G
aRGBBild(yCoord, round(xVehicle_img(i)), 3) = 255; % B
end
end
end
end
% Ergebnis im Video speichern
writeVideo(outputVideo, aRGBBild);
end
% Video-Schreibobjekt schließen
close(outputVideo);
% Polynomkoeffizienten speichern
save('Spurpolynom.mat', 'PolyCoeffsHistory');
%% Hilfsfunktion
function PolynomKoeffizienten = interpoliereFahrspur(aWegpunkte, n)
% Berechnung der kleinsten Quadrate Lösung für die n-te Ordnung der Polynominterpolation
A = ones(size(aWegpunkte, 2), n + 1);
for k = 1:n
A(:, k) = aWegpunkte(1, :).^(n + 1 - k);
end
b = aWegpunkte(2, :)';
PolynomKoeffizienten = A \ b; % Kleinste Quadrate Lösung
end