AlphaBot: Gesteuerte Geradeausfahrt: Unterschied zwischen den Versionen

Aus HSHL Mechatronik
Zur Navigation springen Zur Suche springen
← Zum vorherigen Versionsunterschied
Keine Bearbeitungszusammenfassung
 
(11 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 1: Zeile 1:
[[Kategorie:Arduino]]
[[Kategorie:Arduino]]
[[Kategorie:AlphaBot]]
[[Kategorie:AlphaBot]]
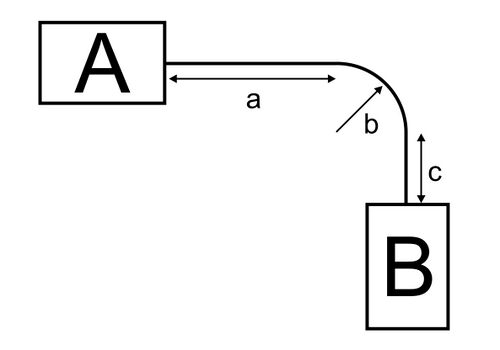
[[Datei:Zwischenprüfung2025.jpg|thumb|rigth|500px|Abb. 1: Programmier-Challenge II (Fehler in Skizze: letzte Gerade 20 cm)]]
[[Datei:Zwischenprüfung2025.jpg|thumb|rigth|500px|Abb. 1: FTF Fahrstrecke]]
{|class="wikitable"
{|class="wikitable"
|-
|-
Zeile 11: Zeile 11:
|}
|}


== Inhalt ==
= Inhalt =
* Autonome Mobile Roboter müssen zur Erfüllung von Aufgaben im Raum navigieren. Der einfachste Weg ist über Odometrie. In dieser Lektion fahren wir feste Figuren im Raum ab.
Autonome Mobile Roboter müssen zur Erfüllung von Aufgaben im Raum navigieren. Der einfachste Weg ist über Odometrie. In dieser Lektion fahren wir feste Figuren im Raum ab. Sie haben den Auftrag bekommen ein Fahrerloses Transportfahrzeug (FTF) zu entwickeln. Nutzen Sie den AlphaBot um die Funktion Ihrer Programmierung nachzuweisen.  
== Lernziele==
== Lernziele==
Nach Durchführung dieser Lektion können Sie
Nach Durchführung dieser Lektion können Sie
* Ihren Roboter eine vorgegebene Strecke geradeaus fahren lassen.
* Ihren Roboter eine vorgegebene Strecke geradeaus fahren lassen.
* Ihren Roboter eine vorgegebenen Kurve fahren lassen.
* Messwerte in einer Textdatei speichern.
* Ihren Roboter auf der Stelle um einen vorgegebenen Winkel drehen lassen.
* Messwerte mit MATLAB<sup>®</sup> analysieren.
* Messwerte auf dem OLED Display anzeigen lassen.
* Bei Objekten im Fahrschlauch eine Notbremsung durchführen.


== Vorbereitung ==
== Vorbereitung ==
* Planen Sie jede Aufgabe als PAP.
* Schauen Sie Ihre Ergebnisse der Programier-Challenge I an, kopieren Sie diese in den Ordner <code>Termin_06</code>.
* Nehmen Sie das OLED Display anhand des Beispiels <code>E22_OLED_Display</code> in Betrieb.
* Optimieren Sie die Kopie bis alles lauffähig ist.


== Versuchsdurchführung ==
= Versuchsdurchführung =
=== Aufgabe 7.0: Demo ===
== Aufgabe 6.1: Geradeausfahrt von Feld A zu Feld B ==
Prof. Schneider zeigt eine mögliche Lösung der Programmierchallenge als Software-Walkthrough. Sie bekommen im Anschluss die Möglichkeit Ihre Lösung zu optimieren, um das Gelernte zu vertiefen.
# Das FTF muss exakt 1,5 m kontinuierlich vorwärts geradeaus von Feld A zu Feld B fahren (a=1,5 m, b=0 m, c=0 m, vgl. Abb. 1).
# Das FTF muss langsam anfahren, so dass erst nach 20 cm die Maximalgeschwindigkeit erreicht wird und 20 cm vor dem Ziel verzögern.
# Die Messwerte ''Zeitstempel in s'' und die gefahrene Strecke des linken und rechten Rades müssen in der ASCII-Datei <code>Geradeausfahrt.txt</code> gespeichert werden.


=== Aufgabe 7.1: Schleife - Fahre Dreieck ===
Arbeitsergebnis: <code>FTF.ino</code>
[[Datei:FahreDreieck.jpg|right|thumb|250px|Abb. 2: Gleichschenkliges Dreieck]]
# Erweitern Sie Ihr bisheriges Programm, um die Seiten eines Dreiecks abzufahren (vgl. Abb. 2).
# Die Seitenlänge a ist eine Variable und soll 30&thinsp;cm betragen.
# Führen Sie eine Schleife 3x aus, die aus Geradeausfahrt und Drehung besteht.
# Stellen Sie die gefahrene Strecke auf dem OLED Display dar.


Arbeitsergebnis: <code>fahreDreieck.ino</code>
== Aufgabe 6.2: Analyse der Streckendaten ==
In MATLAB<sup>®</sup> muss aus der Strecke die Geschwindigkeit und Beschleunigung des AMR berechnet und als Plot (1x3) untereinander Strecke in m, Geschwindigkeit in <math>\frac{m}{s}</math> und Beschleunigung in <math>\frac{m}{s^2}</math> über der Zeit in s dargestellt werden.


{| role="presentation" class="wikitable mw-collapsible mw-collapsed"
Was fällt Ihnen auf?
| <strong>Tipp 1&thinsp;</strong>
 
|-
Arbeitsergebnisse: <code>Geradeausfahrt.txt</code>, <code>zeigeMesswerte.m</code>
| Nutzen Sie die Demos E01, E15, E22 im SVN-Verzeichnis.
|-
| Kapseln Sie Quelltext, der sich häufig wiederholt in Funktionen. Ein Beispiel hier für finden Sie unter den Beispielen E33_Unterfunktion.Wenn Sie beispielsweise das Quadrat programmieren,
programmieren Sie zwei Funktionen void <code>fahreGeradeaus(float Strecke_f32)</code>, um die Strecke a geradeaus zu fahren und void <code>dreheRoboter(float Winkel_f32)<code>, um den
AlphaBot um den Winkel <math>\Psi<math> zu drehen. Beide Funktionen können Sie anschließend in den nachfolgenden Aufgaben mit neuen Parametern wiederverwenden. Das spart enorm viel Zeit
und ist weniger fehleranfällig, wenn Sie Ihre Funktionen getestet haben. Eine Drehung im Uhrzeigersinn ist negativ.
|}


=== Aufgabe 7.2: Variablen nutzen ===
== Aufgabe 6.3: Geregelte Geradeausfahrt ==
Der Roboter soll eine quadratische Fläche komplett abfahren, dabei wird die Kantenlänge des
Nutzen Sie die Erkenntnisse aus Aufgabe 6.2, um geregelt geradeaus zu fahren. Vergleichen Sie hierzu die gefahrene Strecke beider Räder. Ist diese gleichgroß, fährt der AlphaBot eine Gerade. Verändern Sie adaptiv die Motorgeschwindigkeit abhängig von der Streckenabweichung.
Quadrats immer geringer (vgl. Abb. 1). Die Aufgabe eignet sich auch um eine komplette Fläche abzusuchen
z.&thinsp;B. um Gegenstände in einem definierten Bereich zu finden.


'''Arbeitsergebnis:''' <code>fahreSchnecke.ino</code>
== Aufgabe 6.4: Hinderniserkennung ==
Ein Hindernis erscheint plötzlich in Ihrem Fahrschlauch. Sie reagieren mit einer Notbremsung, um den Unfall zu vermeiden. Verlässt das Hindernis die Fahrbahn, kann die geplante Fahrt weitergehen.
# Nutzen Sie <code>fahreZumStartpunkt.ino</code> aus Übungsaufgabe 6.1.
# Stoppen Sie, falls weniger als 20&thinsp;cm vor Ihnen ein Hindernise auftaucht/steht (Notbremse).
# Fahren Sie weiter, sobald das Hindernis entfernt wurde.
# Fehlbremsungen müssen durch geeignete Signalfilterung (z.&thinsp;B. Tiefpassfilter) vermieden werden.
'''Arbeitsergebnis''': <code>Notbremsassistent.ino</code>
{| role="presentation" class="wikitable mw-collapsible mw-collapsed"
{| role="presentation" class="wikitable mw-collapsible mw-collapsed"
| <strong>Tipp 1&thinsp;</strong>
| <strong>Tipps&thinsp;</strong>
|-
|-
| Nutzen Sie die Demos E01, E15, E22 im SVN-Verzeichnis.  
| Drehen Sie den Ultraschall auf 90&thinsp;° (in Fahrrichtung geradeaus).
|-
|-
| Nutzen Sie die Ihre Funktionen aus den vorherigen Aufgaben.
| Wird ein Hindernis detektiert wird die Fahrt umgehend '''pausiert'''. Speichern Sie den Zustand.
|-
| Wird ein Hindernis entfernt wird die Fahrt wieder '''weitergeführt'''. Beispiel: Die Fahrstrecke beträgt 1&thinsp;m geradeaus. Zum Zeitpunkt der Notbremsung wurden bereits 50&thinsp;cm gefahren. Ist das Hindernis entfernt, fahren Sie 50&thinsp;cm weiter.
|}
|}


=== Aufgabe 7.3: Der Rasen von Wimbledon ===
'''Arbeitsergebnis''': <code>FTF_mit_Hinderniserkennung.ino</code>
Schreiben Sie ein Programm, das in immer gleichen Abständen parallele Bahnen mäht (vgl. Abb. 2 und Abb. 3).
[[Datei:Wimbledon.jpg |right|thumb|250px|Abb. 3: Der Rasen von Wimbledon]]
[[Datei:Wimbledon2.jpg |right|thumb|250px|Abb. 4: Parallele Bahnen]]


'''Arbeitsergebnis:''' <code>maeheRasen.ino</code>
== Aufgabe 6.5: Nachhaltige Doku ==
 
{| role="presentation" class="wikitable mw-collapsible mw-collapsed"
| <strong>Tipp 1&thinsp;</strong>
|-
| Nutzen Sie die Demos E01, E15, E22 im SVN-Verzeichnis.
|-
| Nutzen Sie die Ihre Funktionen aus den vorherigen Aufgaben.
|}
=== Aufgabe 7.4: Nachhaltige Doku ===
* Sichern Sie alle Ergebnisse mit beschreibendem Text (<code>message</code>) in SVN.
* Sichern Sie alle Ergebnisse mit beschreibendem Text (<code>message</code>) in SVN.
* Halten Sie die Regeln für den [[Software_Versionsverwaltung_mit_SVN|Umgang mit SVN]] ein.
* Halten Sie die Regeln für den [[Software_Versionsverwaltung_mit_SVN|Umgang mit SVN]] ein.
Zeile 85: Zeile 70:
'''Arbeitsergebnis''' in SVN: <code>SVN Log</code>
'''Arbeitsergebnis''' in SVN: <code>SVN Log</code>


<!--
= Demos =
== Tutorials ==
-->
 
== Demos ==
* <code>E01_MotorenTest</code>
* <code>E01_MotorenTest</code>
* <code>E15_RadInkrementalgeberFahrt</code>
* <code>E15_RadInkrementalgeberFahrt</code>
* <code>E22_OLED_Display</code>
* <code>E33_Unterfunktion</code>
* <code>E33_Unterfunktion</code>


== Literatur ==
 


----
----
→ Termine [[Einführungsveranstaltung_Informatikpraktikum_2_im_SoSe_2025|1]] [[AlphaBot:_Hardware_Support_Package_für_MATLAB|2]] [[AlphaBot: Servo_mit_MATLAB_ansteuern|3]] [[AlphaBot:_Motoren_und_Inkrementalgeber|4]] [[AlphaBot: Programmier-Challenge I SoSe25|5]] [[AlphaBot:_Gesteuerte_Geradeausfahrt|6]] [[AlphaBot: Geregelte Fahrt mit Linienverfolger|7]] [[AlphaBot: Parklücke suchen|8]] [[AlphaBot: Autonomes Einparken|9]] [[AlphaBot: Programmier-Challenge II SoSe25|10]]<br>
→ Termine [[Einführungsveranstaltung_Informatikpraktikum_2_im_SoSe_2025|1]] [[AlphaBot:_Hardware_Support_Package_für_MATLAB|2]] [[AlphaBot: Servo_mit_MATLAB_ansteuern|3]] [[AlphaBot:_Motoren_und_Inkrementalgeber|4]] [[AlphaBot: Programmier-Challenge I SoSe25|5]] [[AlphaBot:_Gesteuerte_Geradeausfahrt|6]] [[AlphaBot: Geregelte Fahrt mit Linienverfolger|7]] [[AlphaBot: Parklücke suchen|8]] [[AlphaBot: Autonomes Einparken|9]] [[AlphaBot: Programmier-Challenge II SoSe25|10]]<br>
→ zurück zum Hauptartikel: [[AlphaBot_SoSe25|Informatik Praktikum 2]]
→ zurück zum Hauptartikel: [[AlphaBot_SoSe25|Informatik Praktikum 2]]

Aktuelle Version vom 15. Mai 2025, 12:18 Uhr

Abb. 1: FTF Fahrstrecke
Autor: Prof. Dr.-Ing. Schneider
Modul: Praxismodul II
Lehrveranstaltung: Mechatronik, Informatik Praktikum 2, 2. Semester

Inhalt

Autonome Mobile Roboter müssen zur Erfüllung von Aufgaben im Raum navigieren. Der einfachste Weg ist über Odometrie. In dieser Lektion fahren wir feste Figuren im Raum ab. Sie haben den Auftrag bekommen ein Fahrerloses Transportfahrzeug (FTF) zu entwickeln. Nutzen Sie den AlphaBot um die Funktion Ihrer Programmierung nachzuweisen.

Lernziele

Nach Durchführung dieser Lektion können Sie

  • Ihren Roboter eine vorgegebene Strecke geradeaus fahren lassen.
  • Messwerte in einer Textdatei speichern.
  • Messwerte mit MATLAB® analysieren.
  • Bei Objekten im Fahrschlauch eine Notbremsung durchführen.

Vorbereitung

  • Schauen Sie Ihre Ergebnisse der Programier-Challenge I an, kopieren Sie diese in den Ordner Termin_06.
  • Optimieren Sie die Kopie bis alles lauffähig ist.

Versuchsdurchführung

Aufgabe 6.1: Geradeausfahrt von Feld A zu Feld B

  1. Das FTF muss exakt 1,5 m kontinuierlich vorwärts geradeaus von Feld A zu Feld B fahren (a=1,5 m, b=0 m, c=0 m, vgl. Abb. 1).
  2. Das FTF muss langsam anfahren, so dass erst nach 20 cm die Maximalgeschwindigkeit erreicht wird und 20 cm vor dem Ziel verzögern.
  3. Die Messwerte Zeitstempel in s und die gefahrene Strecke des linken und rechten Rades müssen in der ASCII-Datei Geradeausfahrt.txt gespeichert werden.

Arbeitsergebnis: FTF.ino

Aufgabe 6.2: Analyse der Streckendaten

In MATLAB® muss aus der Strecke die Geschwindigkeit und Beschleunigung des AMR berechnet und als Plot (1x3) untereinander Strecke in m, Geschwindigkeit in ms und Beschleunigung in ms2 über der Zeit in s dargestellt werden.

Was fällt Ihnen auf?

Arbeitsergebnisse: Geradeausfahrt.txt, zeigeMesswerte.m

Aufgabe 6.3: Geregelte Geradeausfahrt

Nutzen Sie die Erkenntnisse aus Aufgabe 6.2, um geregelt geradeaus zu fahren. Vergleichen Sie hierzu die gefahrene Strecke beider Räder. Ist diese gleichgroß, fährt der AlphaBot eine Gerade. Verändern Sie adaptiv die Motorgeschwindigkeit abhängig von der Streckenabweichung.

Aufgabe 6.4: Hinderniserkennung

Ein Hindernis erscheint plötzlich in Ihrem Fahrschlauch. Sie reagieren mit einer Notbremsung, um den Unfall zu vermeiden. Verlässt das Hindernis die Fahrbahn, kann die geplante Fahrt weitergehen.

  1. Nutzen Sie fahreZumStartpunkt.ino aus Übungsaufgabe 6.1.
  2. Stoppen Sie, falls weniger als 20 cm vor Ihnen ein Hindernise auftaucht/steht (Notbremse).
  3. Fahren Sie weiter, sobald das Hindernis entfernt wurde.
  4. Fehlbremsungen müssen durch geeignete Signalfilterung (z. B. Tiefpassfilter) vermieden werden.

Arbeitsergebnis: Notbremsassistent.ino

Arbeitsergebnis: FTF_mit_Hinderniserkennung.ino

Aufgabe 6.5: Nachhaltige Doku

Arbeitsergebnis in SVN: SVN Log

Demos

  • E01_MotorenTest
  • E15_RadInkrementalgeberFahrt
  • E33_Unterfunktion


→ Termine 1 2 3 4 5 6 7 8 9 10
→ zurück zum Hauptartikel: Informatik Praktikum 2

Abgerufen von „https://wiki.hshl.de/wiki/index.php?title=AlphaBot:_Gesteuerte_Geradeausfahrt&oldid=135617“