OSE - Objekt - und Spurerkennung

Spurerkennung

Workflow und Vorgehen

Um schnellere Ergebnisse zu erzielen und ein leichteres Umsetzen der eigenen Ansätze zu ermöglichen wurde entschieden, die Algorithmen in Matlab zu entwickeln und auf Funktionalität zu prüfen. Anschließend wurden diese dann in C/C++ Code umgesetzt und in das Projekt mit eingebunden. Die folgenden Abschnitte beschreiben welche Voraussetzungen geschaffen wurden, um diesen Entwicklungsansatz umzusetzen.

Modellbasierte Entwicklung in Matlab

Matlab stellt mit seinen Toolboxen eine große Funktionsvielfalt im Bereich der Bildverarbeitung zur Verfügung. Diese erleichtern das Umsetzen von eigenen Ansetzen. Einfache Darstellung und Visualisierung vereinfachen insbesondere die Fehlersuche. Um auf der späteren Zielhardware zu funktionieren, werden die Algorithmen mit Hilfe Videos entwickelt, das mit einer Kamera aufgenommen wurde, die baugleich mit am Auto verbauten ist.

Die fertigen Algorithmen, die der Bildverarbeitung dienen, müssen so aufgebaut sein, dass sie auf Datenbasis eines S/W Kantenbildes arbeiten. Alle Funktionen, die der Umformung des Bildes dienen, müssen ausgelagert werden.

Um die in Matlab entworfenen Algorithmen in das C++ Projekt zu übernehmen, gibt es die Möglichkeit den Embedded Coder zu nutzen. Dieser ermöglicht es aus Matlab Code C / C++ Code zu generieren. Eine Anleitung zum Generieren von C Code findet sich in dem Artikel "Von Matlab zu C Code" Um den Code im "Objekt_Spurerkennung" Projekt zu verwenden, muss unter dem Punkt "Dateien ins Projekt übernehmen" des Artikels "Von Matlab zu C Code" "C/C++ Dynamic Libary" statt "C/C++ Static Libary" gewählt werden.

Bestimmte Matlab Funktionen lassen sich nicht generieren. Hier müssen eigene Funktionen in Matlab programmiert werden um diese zu ersetzen. Eine andere Möglichkeit ist das Einsetzen von Dummyfunktionen in Matlab Code. Diese Dummyfunktionen enthalten keine Funktionalität sondern dienen nur als Platzhalter deren Funktionsaufruf im C/C++ Projekt dann durch den Aufruf der jeweiligen in C / C++ umgesetzten Funktion ersetzt wird.

Umsetzung in C Code

Vorausetzungen zum übernehmen der Matlab Algorithmen

Die Grundlage des hier vorgestellten Vorgehens ist, dass die Datenbasis für beide Entwicklungsschritte gleich ist. So muss gewährleistet sein, dass die Bilder der Kamera und die aus dem in Matlab verwendeten Video einer Rundfahrt, vor dem Verwenden durch die Algorithmen zur Spur- und Stoplinienerkennung in ein einheitliches Bildformat konvertiert werden.

Schaffen gleicher Datenbasis

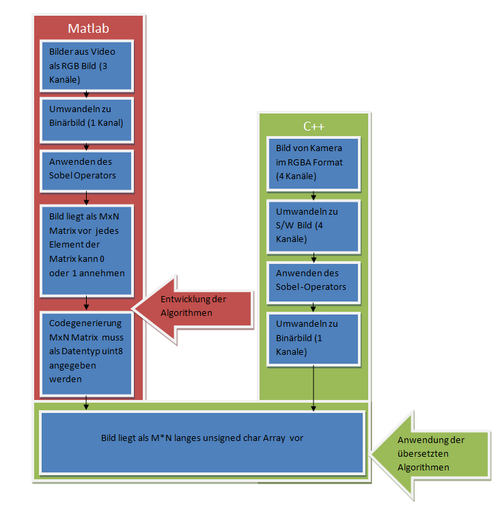
In der Matlab Umgebung werden die Video Frames mit der Auflösung 752*478 eingelesen und in die Matrix Frame gespeichert. Das in Frame gespeicherte Bild wird erst in ein Grau- und anschließend in ein S/W Bild umgewandelt. Auf dieses wird Sobel Operator angewendet. Das Ergebnis wird in Frame_bw gespeichert. Frame_bw dient allen in Matlab entwickelten Algorithmen als Datengrundlage und muss bei deren Übersetzung als uint8 Array gespeichert werden.

 % Frame lesen
    Frame = imread(Frame_Name,'PNG');
    Frame = rgb2gray(Frame);

    
 % Vorverarbeitung
    Frame_bw = Gray2BW( Frame , 752, 478 );
    Frame_bw = edge(Frame_bw,'sobel','nothinning');

Im C++ Projekt werden die Bilder von der auf dem Auto verbauten VRmagic Kamera aufgenommen. Um diese mit den Matlab Algorithmen zu bearbeiten sind noch weiter Schritte nötig.Die Abbildung "für die Bildverarbeitung relevanten Schritte" zeigt die Schritte aus der Software "Objekt_Spurerkennung" die zur Bildverarbeitung nötig sind.

für die Bildverarbeitung relevanten Schritte

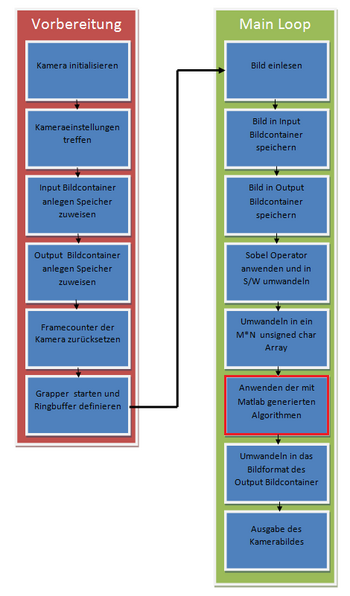
Im linken Teil des Bildes sind die Initialisierungsschritte dargestellt. Zuerst muss die Verbindung zur Kamera aufgebaut und Einstellungen wie z.B. die Belichtungszeit gesetzt werden. Anschließend werden Bildcontainer für das Quell- (p_gray_src_img) und das Ausgabebild(p_out_img) angelegt. Das Quellbild wird im Bildfromat "VRM_GRAY_8" gespeichert. Somit kann die Umwandlung von RGB zu Grau entfallen.

    VRmImage* p_gray_src_img = 0;
    VRmImageFormat gray_format;
    gray_format.m_width = 752;
    gray_format.m_height = 478;
    gray_format.m_color_format = VRM_GRAY_8;
    gray_format.m_image_modifier = 0;

 // allocation of gray level source image, use VRmUsbCamFreeImage to free images allocated with VRmUsbCam Lib
    if(!VRmUsbCamNewImage(&p_gray_src_img, gray_format))
        LogExit();

Das Ausgabebild muss in einem mit der Ausgabe auf dem Bildschirm durch die "SDL Bibliothek" kompatiblem Bildformat vorliegen. Es wird im Format "VRM_ARGB_4X8" gespeichert. Weiter Informationen über die verwendbaren Formate finden sich in der Datei "vrmusbcam2.h".

    // allocation of gray level image for output in SDL window, use VRmUsbCamFreeImage to free images allocated with VRmUsbCam Lib
    VRmImage* p_out_img = 0;
    VRmImageFormat bgr888_format;
    bgr888_format.m_width = 752;
    bgr888_format.m_height = 478;
    bgr888_format.m_color_format = VRM_ARGB_4X8;
    bgr888_format.m_image_modifier = 0;

    if(!VRmUsbCamNewImage(&p_out_img, bgr888_format))
        LogExit();

Nach dem Anlegen der Bildcontainer wird der Framecounter der Kamera zurückgesetzt und der "Grabber" zum holen der Bilder gestartet. Im Anschluss wird die Main Loop gestartet und zyklisch ausgeführt. Zu Beginn jedes Zyklus wird ein neues Bild von der Kamera geladen und anschließend in p_gray_src_img konvertiert. Um es später auszugeben wird p_gray_src_img in das Output Bildformat konvertiert und als p_out_img gespeichert.

     // lock next (raw) image for read access
        VRmImage* p_source_img = 0;
        VRmDWORD frames_dropped = 0;
        if(!VRmUsbCamLockNextImageEx(device, port, &p_source_img, &frames_dropped))
            LogExit();


     // convert source image into gray image for further processing with VM_LIB
        if(!VRmUsbCamConvertImage(p_source_img, p_gray_src_img))
            LogExit();

     // ... and copy the source image to the output image
	CopyGrayToOutRGB(p_gray_src_img, p_out_img);

Anschließend wird die Funktion "objekt_und_spurerkennung" mit dem Bilder als Parameter aufgerufen. Diese Funktion erlaubt es die aus Matlab generierten Funktionen einzubinden.

        // Kantenerkennung für die entsprechenden Zeilen
	sobel_und_bw(p_gray_src_img, p_gray_out_img, gx, gy, temp_PoI, PoI_size , on_jump );

	// Umwandeln in Bw Typ um einfache überführung von Matlab zuermöglichen 
	umwandeln_bw_bild_hin(p_gray_out_img->mp_buffer, Frame_bw_einzeilig);

	// Finde die Spurkoordinaten im ROI
	spur_finden(p_gray_src_img, Frame_bw_einzeilig, x, y, index, temp_PoI, PoI_size, on_jump,PoI_default,gx,gy);

	// Berechnung und Filterung des Schwerpunktes in X-Richtung des POI
	kalmanfilter(index, iterator, temp_PoI, PoI_default);


	Entfernung=finde_stoplinie(Frame_bw_einzeilig,&Stoplinie,&Trefferzeile);
		
	//Transformiere die Bildkoordinaten in Weltkoordinaten
	koordinatentransformation(index, x, y, Kanten_Spur_x, Kanten_Spur_y, Kanten_Spur_g);

	//Bestimme aus den Weltkoordinaten ein Polynom und verschiebe auf Sollspur
	valide_funktion = polynombestimmung(index, temp_koeff, Kanten_Spur_g ,verschiebung[iterator]);

	// Zurück Umwandeln aus Bw Typ zur Darstellung 
	umwandeln_bw_bild_zurueck(p_gray_out_img->mp_buffer, Frame_bw_einzeilig);

Zuerst wird mit Hilfe der Funktion "sobel_und_bw" der Sobel Operator auf die relevanten Zeilen des entsprechenden ROIs angewendet und ein Kantenbild erstellt. Anschließend wird durch eine Schwellwertentscheidung das Kantenbild in ein S/W Bild umgerechnet und in dem VRM_ARGB_4X8 Format des Output Bildcontainers gespeichert. Zu beachten ist hierbei der unterschiedliche "pitch" der Bildformate.Dieser gibt an wie viele Bytes einen Pixel repräsentieren. Das VRM_GRAY_8 ist ein 8 Bit Format; jeder Pixel wird durch ein Byte dargestellt. Das VRM_ARGB_4X8 ist ein 32 Bit Format; hier wird jeder Pixel durch 4 Bytes beschrieben. Dieses setzt sich aus 4 Kanälen (jeder entspricht einem Byte pro Pixel) : dem Alphakanal, dieser gibt die Transparenz an, und den 3 Farbkanälen Rot, Grün und Blau. Um das VRM_GRAY_8 in das VRM_ARGB_4X8 Format umzuwandeln, werden Daten des einen Kanals in alle 3 Farbkanäle des neuen Formats geschrieben. Da das Bild keine Transparenz besitzen soll, wird der Alphakanal auf sein Maximum gesetzt.

    p_gray_out_img->mp_buffer[(r) * p_gray_out_img->m_pitch + x * 4 + 0] = (unsigned char)grad;
    p_gray_out_img->mp_buffer[(r) * p_gray_out_img->m_pitch + x * 4 + 1] = (unsigned char)grad;
    p_gray_out_img->mp_buffer[(r) * p_gray_out_img->m_pitch + x * 4 + 2] = (unsigned char)grad;
// Alphakanal hoch setzen --> Transparenz 
   p_gray_out_img->mp_buffer[(r) * p_gray_out_img->m_pitch + x * 4 + 3] = 255;

Mit der Funktion "umwandeln_bw_bild_hin" ist es möglich das Bild aus dem VRM_ARGB_4X8 Format in ein für die mit Matlab generierten Funktionen kompatibles Bildformat umzuwandeln.

Die Funktion "spur_finden" ermittelt dann anschließend alle Spurpunkte, die sich in dem ROI befinden. Hier ist zu beachten das zu Beginn die Zeilen noch oben hin untersucht werden. Wenn die oberste Zeile des ROIs erreicht wurde, spring der Algorithmus in die erste Zeile des ROIs zurück und sucht dann den Teil unterhalb des ROIs nach möglichen Spurpunkten ab. Dieser letzte Schritt ist notwendig, da die Punkte nahe des Fahrzeuges als besonders bedeutend einzustufen sind.

Nachdem dann alle Spurpunkte ermittelt wurden, wird mittels des Funktion "kalmanfilter" der neue Schwerpunkt des ROIs aus den gefundenen Spurpunkten berechnet und anschließend mit dem Kalmanfilters gefiltert. Denn so wandert der jeweilige ROI mit dem Spurverlauf mit und das Risiko keine Spur zu finden wird minimiert.

Die Koordinatentransformation der Bildpunkte in die Kamerakoordinaten führt die Funktion "koordinatentransformation" durch. Anschließend wird aus den realen Spurpunkten eine Polynom interpoliert mittels der Funktion "valide_funktion". Dieses Polynom wird schlussendlich noch in das Sollpolynom linksverschoben von der rechten Fahrbahnmarkierung umgerechnet.

Die Umkehrung der Funktion "umwandeln_bw_bild_hin" erlaubt die Funktion "umwandeln_bw_bild_zurueck". Um diese Funktionen nutzen zu können, muss das Bild als S/W Kantenbild im VRM_ARGB_4X8 Format bereitgestellt werden. Nach dem Umwandeln in das Ausgabeformat werden in das Bild gefundene Spurpixel Rot gekennzeichnet und das Bild ausgegeben.

Übernahme der Matlab Algorithmen

Die Struktur des C++ Projektes ermöglicht es einfach neue Module hinzuzufügen. Dies gilt sowohl für Matlab-generierte Module als auch für handgeschriebe Module wie z.B. Komunikation. Dieser Teil zeigt wie ein zuvor nach dem Artikel "Von Matlab zu C Code" erzeugtes Modul integriert wird. Nach dem Generieren liegt in dem zum generieren angelegten Projektordner der Ordner "codegen" vor. Dieser beinhaltet den Ordner "dll". Dies steht für Dynamic Link Library. Ist dies nicht der Fall muss der Code erneut als "C/C++ Dynamic Libary" generiert werden. Ist er vorhanden, enthält er den Ordner mit dem gewählten Modulnamen. Dieser wird in die in Abbildung "Projekt Struktur" gezeigten Struktur in den Ordner Module hinzugefügt.

Projekt Struktur

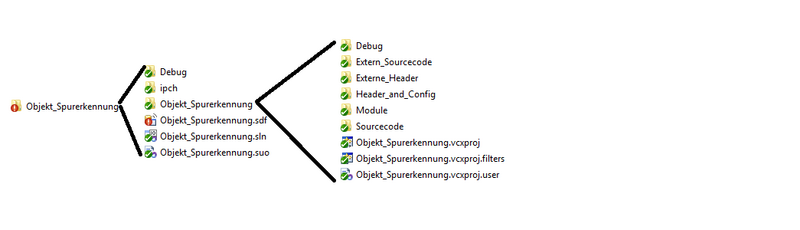
Anschließend müssen entweder alle Dateien aus dem Ordner bis auf "Modulname.c", "Modulname.h" und "Modulname_types.h" gelöscht werden. Oder es werden alle Dateien zur Nachvollziehbarkeit gespeichert. In das Visual Studio Projekt werden nur "Modulname.c", "Modulname.h" und "Modulname_types.h" hinzugefügt da alle anderen Daten entweder nicht relevant sind oder bereits existieren. Da das Projekt als C++ Projekt angelegt ist, muss die ".c" in eine ".cpp" Datei umbenannt werden. In Visual Studio ist das Projekt in dieselbe Struktur geteilt in der es auch im Ordner abgelegt ist. Es wird jedoch zwischen ".h" und".c"

Dateien unterschieden. Dementsprechend muss der Modulordner sowohl unter Headerdatein als auch unter Quelldateien hinzugefügt werden.

Visual Studio Projektstruktur

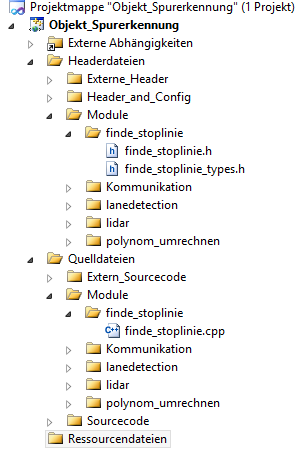
Anschließend muss der Modulordner als zusätzliches Inventarverzeichnis hinzugefügt werden. Dies wird in dem Menü Projekteigenschaften vorgenommen. Nach einem Rechtsklick auf Objekt_Spurerkennung (siehe Abb. Visual Studio Projektstruktur) öffnet sich ein Kontextmenü in dem der letzte Punkt "Eigenschaften" gewählt werden muss. Anschließend öffnet sich das gesuchte Menü.

Objekt_Spurerkennung-Eigenschaftenseiten

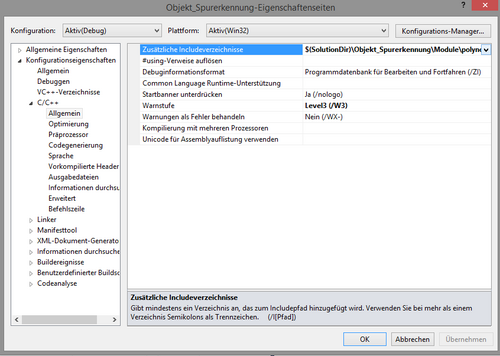
In diesem muss unter zusätzliche Inventarverzeichnisse der Modulordner hinzugefügt werden. Nachdem das Modul erfolgreich in das Projekt eingefügt wurde, müssen nun noch Code-Anpassungen vorgenommen werden. Falls in Matlab Dummyfunktionen für in C++ bereits vorhandene Funktionen eingebaut wurden, müssen diese jetzt durch ihre C++ Funktionen ersetzt werden. Ebenso müssen die Includes der Header "Modulname_initialize.h" und "Modulname_terminate.h" entfernt werden. Da bestimmte Matlab Funktionen nicht generierbar sind, kann es zu weiteren Änderungen im Code kommen. Es empfiehlt sich dies gut hervorzuheben und durch Kommentare zu rechtfertigen.

Umsetzung

Spur finden und auswerten

Damit das Fahrzeug innerhalb einer Fahrbahn geregelt fahren kann, muss in irgendeiner Form der Verlauf der Strecke wahrgenommen werden. Dies funktioniert kameragestützt. Der Ansatz zur Spurerkennung orientiert sich an den sogenannten "regions of interest" (ROI). Diese ROIs sind definierte, aber auch dynamsiche Bildauschnitte, in denen die jeweiligen Fahrbahnmarkierungen gesucht werden. Momentan ist ein ROI für die rechte und die linke Fahrbahnmarkierung implementiert. Die Mittellinie wird nicht berücksichtigt, weil sie lediglich aus unterbrochenen Abschnitten besteht. Der allgemeine Algorithmus weist folgenden Ablauf auf:

PAP ROI-Auswahl

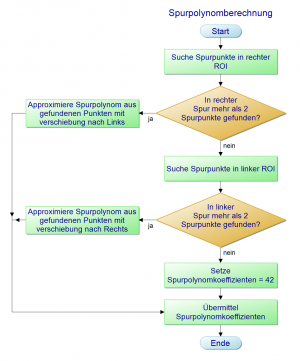
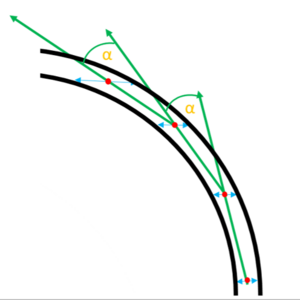
Innerhalb jedes ROIs werden dann die relevanten Punkte der Fahrbahnmarkierung bestimmt. Hierzu startet der Spurerkennungsalgorithmus mittig in der untersten Zeile. Je nach Parametrierung werden die Zeilen dann nach rechts oder links auf mögliche Spurpunkte untersucht. Ein valider Spurpunkt muss zwei Bedingungen erfüllen. Zum einen müssen in der Zeile zwei Kantenübergänge gefunden werden, die auch einen maximalen Abstand voneinander nicht überschreiten dürfen. Ist dies erfüllt wird die Mitte als vorläufiger Spurpunkt angenommen. In der darauf anschließenden Bedingung darf der Winkel zwischen dem aktuellen und dem alten Richtungsvektor nicht mehr als 45° betragen. Ist der linke bzw.rechten Rand des ROIs überschritten oder ist ein valider Spurpunkt gefunden, springt der der Algorithmus um den aktuellen Richtungsvektor verschoben intervallmäßig mittig in die nächste zu untersuchende Zeile.

Spurpunktverifizierung

PAP Spurpunktfindung

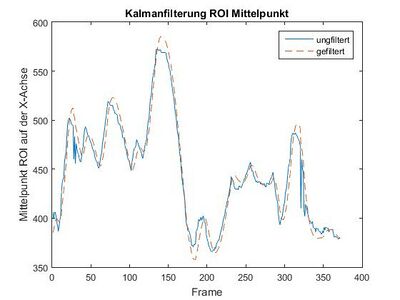
Kalman Filter

Da die Fahrbahnmarkierung dynamisch im Kamerbild wandert, ist es sinnvoll auch die ROIs in X-Richtung des Bildes zu verschieben. Daher wird der Mittelwert aller X-Koordinaten eines der Fahrbahnspurpunkte ROIs ermittelt. Anschließend wird dieser Schwerpunkt noch mit einem Kalmanfilter gefiltert, um Sprünge zu dämpfen und hochfrequente Verschiebungen zu dämpfen. Der Vorteil des Kalmanfilters liegt darin, dass er nicht immer den realen Werten "hinterherläuft".

Kalmanfilterung der ROI Mittelpunkte

Polynom berechnen

Die gefundenen Fahrbahnpunkte werden durch ein Polynom zweiten Grades interpoliert. Dabei kommt die Methode der kleinsten Fehlerquadrate zu Einsatz.

Das Spurpolynom, das durch die Kamera ermittelt wird, beschreibt den Verlauf der rechten oder linken äußeren Fahrspur. Das Fahrzeug selbst soll aber in der Mitte der rechten Fahrbahn geregelt fahren. Dafür müsste das Polynom den Verlauf der Fahrbahnmitte beschreiben. Da dort jedoch keine Daten zu ermitteln sind, muss das gefundene Polynom umgerechnet werden.

Ein sehr simpler Ansatz wäre das Polynom einfach um 20cm nach links bzw. 60 cm nach rechts zu verschieben, weil dies exakt die Hälfte der Fahrbahnbreite ist. In der Implementierung würde dies bedeuten, dass lediglich der Wert C (ax²+bx+c) um diese bestimmten cm korrigiert werden muss. Auf gerader Strecke ist diese Umformung sogar fehlerfrei. In Kurven würde dies aber Ungenauigkeiten bedeuten, da sich hier auch die Krümmungen der Parabeln für die Fahrbahnmitte und die Außenlinie unterscheiden.

Um dieses Problem zu lösen muss ein anderer Ansatz gewählt werden. Ziel ist es nun zu jedem Punkt auf der ursprünglichen Parabel den entsprechenden Punkt auf dem neuen Polynom bestimmen zu können. Dabei wird die Straßengeometrie ausgenutzt.

Zunächst wird ein Wert in das ursprüngliche Polynom eingesetzt. Dieser Wert sollte sinnvollerweise in dem Bereich liegen in dem das Polynom auch die Fahrspur beschreibt. Es ergibt sich also ein Punkt mit den Werten X und Y auf der Außenlinie. Über den korrelierenden Punkt des Zielpolynoms ist nun bekannt das er in einer euklidischen Distanz von 20cm bzw 60 cm zum Ausgangspunkt liegt. Als nächstes wird die Ableitung in diesem zuvor eingesetzten Punkt berechnet. Am Beispiel des Steigungsdreieckes zur Bestimmung von Ableitungen lassen sich die folgenden Schritte leicht erklären. Es teilt die Steigung in diesem Punkt in eine Strecke in X- und Y-Richtung ein. Da diese rechtwinkling aufeinander stehen, lassen sich die Wikelfunktionen hier anwenden. Die Strecken in X- und Y-Richtung stellen die Katheten in diesem Dreieck dar und ihr Quotient (Tangens) entspricht der Steigung, die zuvor durch Ableiten bereits ermittelt wurde. Es ist also möglich aus der Ableitung wieder die Anteile in X- und Y-Richtung zu bestimmen, indem der Arcustangens angewedet wird. Der Sinus bzw. Cosinus des hieraus resultierenden Winkels ergibt entsprechend die relative Steigung in X- bzw. Y-Richtung. Jeweils mit 20cm oder 60cm multipiziert erhält man die Werte um die der Ausgangspunkt zu verschieben ist, damit er auf dem Zielpolynom liegt.

Wiederholt man diesen Vorgang für mehrere Punkte und interpoliert durch diese anschließend eine neue Parabel, so beschreibt diese den Verlauf der Fahrbahnmitte der rechten Fahrspur.

Stoplinie finden

Damit das Fahrzeug sich gemäß geltender Verkehrsregeln verhalten kann und dementsprechend an Kreuzungen mit Stopplinien anhält, muss es in der Lage sein solche zu erkennen und zu tracken.

Diese Funktionalität wird mit Hilfe der am Fahrzeug montierten VR Magic Kamera umgesetzt. Der Code der Stopplinienerkennung soll dabei in das Programm zur Spurerkennung integriert werden, da die Performance auf diese Weise erheblich gesteigert werden kann. Schließlich müssten andersfalls bildvorverarbeitende Maßnahmen wie z.B. das Sobeln erneuet ausgeführt werden.

Für das Erstellen des Quellcodes zur Stoplinienerkennung wurde zunächst die Annahme getroffen, dass Stoplinien stets eine horizontale weiße und wenige Pixel breite Linie im gesobelten Bildausschnitt darstellen. Darüber hinaus kann davon ausgegangen werden, dass sich diese Linie etwa in der Mitte des Bildes befinden muss, da das Fahrzeug schließlich die Spur halten soll.

Der Algorithmus unterscheidet grundsätzlich zwei Fälle:

- Es liegen aktuell keien Daten zu einer Stoplinie vor
- Es wird aufgrund vorangegangener Frames eine Stoplinie getrackt

Wird keine Linie getrackt, wird eine 18 Elemente lange Spalte in der Bildmitte beginnend an der oberen Kante der gesobelten ROI abgefragt. Stößt man dabei auf einen weißen Pixel, könnte es sich um eine Stoplinie handeln. Um dies zu verifizieren, wird ausgenutzt, dass diese Stoplinie ja horizontal verlaufen müsste. Der Vorgang wird also einige Pixel links und rechts neben diesem ersten Treffer wiederholt. Ist die Suche auch in diesen Fällen erfolgreich, wird fortan davon ausgegangen, dass es sich um eine Stoplinie handelt. Mit Hilfe der Bild_zu_Welt-Funktion, die auch bei der Spurerkennung eingesetzt wird, lässt sich berechnen, wie weit die Stoplinie vom aktuellen Standpunkt noch entfernt ist. Aufgrund der dabei verwendeten Zentralperskektive die in der Bildmitte am genausten ist, wird von den drei Treffern, die bei der Abfrage erzielt wurden, der mittlere genutzt. Dieser Ansatzt nutzt zudem die Tatsache aus, dass bei einer Geradeausfahrt die Stoplinie von oben in das Bild hinein rücken muss. Eine auf diese Weise gefundene Stoplinie ist abhängig davon welches der 18 Elemente der Treffer war noch etwa 1,3m entfernt.

Die Entfernung in Metern wird neben den Spurdaten an die Regelung übermittelt. Intern wird zusätlich die Trefferzeile gespeichert, da mit Hilfe dieser ein Tracking der gefundenen Linie im folgenden Frame möglich ist. Im nächsten Zyklus wird anstatt am oberen Rand der ROI in der Bildzeile gestartet, die im letzten Durchlauf gespeichert wurde. Da das Fahrzug sich zwischen den Bildern etwas nach vorne bewegt hat, sollte die Stoplinie nun etwas weiter unten im Bild zu finden sein. Durch das erneute Abfragen der nächsten 18 Bildzeilen ist relativ sicher, dass die Linie wiedergefunden wird, wenn es sich wirklich um eine Stoplinie gehandelt hat, da dieser Wert sehr wohlwollend gewählt wurde. Auf diese Weise ergibt sich eine neue Trefferzeile für den nächsten Zyklus und damit auch ein neuer Abstand in Metern. Es ist somit möglich die Linie bis etwa 30cm vor das Auto selbst zu tracken, da bei geringeren Abständen das Fahzeug sebst die Linie verdeckt und ein Erkennen so unmöglich macht.

Ist die Suche nach weißen Pixeln einmal nicht erfolgreich bedeutet das entweder, dass in den nächsten ca. 130cm keine Stoplinie ist oder die bisher getrackten Daten nicht zu einer Stoplinie gehören. Der Track wird nach nur einmaligem Fehlschlagen der Suche gelöscht, da dies vorrausetzt, dass er nicht in den folgenden 18 Bildzeilen wiedergefunden werden konnte und dies schließlich ein sehr kulanter Wert ist.

Weitere Ansätze

Kalman Filter

Die bisherige Spurerkennung ist stark fehleranfällig für fehlende Spurelemente. Diese können aufgrund von Lichtreflexen oder Lücken in der Fahrspur entstehen. Um die Spurerkennung robust gegenüber solchen Störungen zu gestalten, wird im folgenden ein Ansatz beschrieben, der die gefundenen Punkte einer Spur auf einen Schwerpunkt reduziert, diesen Mithilfe des Kalman Filters trackt und im nächsten Zyklus nur im Bereich des geschätzten Schwerpunktes sucht. Sollte keine Spurinformation in diesem Bereich vorhanden sein, wird der Wert durch den Kalman Filter bereitgestellt.

Vorbereitung der Bilddaten

Der neue Ansatz der Spurerkennung soll nicht nur robuster sein, sondern auch einen Spurwechsel ermöglichen. Aus diesem Grund wird nicht nur die rechte Fahrbahnbegrenzung sondern auch die Mittellinie getrackt. Im Falle eines Spurwechsels würde die linke und die mittlere Linie verfolgt werden. Zuerst wird das Bild vor verarbeitet. Es wird in ein S/W Bild umgewandelt, mithilfe des Sobel Operators in ein Kantenbild umgewandelt und auf zwei Regionen reduziert. In der Abbildung "links Graubild,mitte ROI,rechts Kantenbild" wurde die Reihenfolge aus Darstellungsgründen vertauscht. Das auf der rechten Seite zu sehende Bild entspricht dem beschrieben Stand.

links Graubild,mitte ROI,rechts Kantenbild

Aus der mittleren Bildspalte heraus, werden 8 Zeilen in den zwei Regionen auf Schwarz/Weiß- Übergänge geprüft. Die linke Region von rechts nach links und die rechte Region von links nach rechts. Unter der Annahme, dass sich das Auto auf einer Fahrspur befindet sind die ersten Übergänge die Begrenzungslinien. Diese gefundenen Punkte werden anhand des Abstandes im Weltkoordinaten zum Mittelpunkt der Autofront verifiziert. Diese werden je Region zu einem Schwerpunkt zusammengefasst und mithilfe des im nächsten Abschnitts beschriebenen Kalman Filters getrackt. Im nächsten Zyklus werden die Regionen abhängig von dem geschätzten Schwerpunkt aufgespannt.

Schwerpunkte tracken

Der Schwerpunkt liegt in Form eines Koordinatenpaares (x/y) vor und soll nun getrackt werden. Dies wird mit Hilfe eines Kalman Filters umgesetzt. Dieses muss für diese Anwendung nur noch parametrisiert werden, da die einzelnen Berechnungsschritte stets dieselben sind. Wir wählen also den Ansatz das unser System über 4 Zustände verfügt:

- x-Position des Schwerpunkts
- Geschwindigkeit in x-Richtung
- y-Position des Schwerpunkts
- Geschwindigkeit in y-Richtung

Die Positionen können hierbei gemessen werden während die Geschwindigkeiten lediglich aufgrund der Positionsänderung geschätzt werden. Dies entspricht also einem einfachen physikalischem Modell, sodass sich die Systemmatrix wie folgt erstellen lässt:

  A = [ 1  dt  0   0
        0  1   0   0
        0  0   1  dt
        0  0   0   1 ];

Dies soll als physikalische Grundlage genügen. Da somit eine Dynamik im Modell entfällt, kann die Matrix B zu Null gewählt werden. Die Messmatrix ergibt sich für die einzelnen Systemzustände zu 1 für direkt gemessene Elemente und zu 0 für lediglich indirekt beobachtete Komponenten. Um mit dem Filter gute Ergebnisse zu erzielen, muss schließlich noch betrachtet werden wie sehr das Filter den Messwerten bzw. dem System vertrauen soll. Hierbei haben diverse Versuche zu der Erkenntnis geführt, dass die folgenden Einstellungen das Filter befähigen, die Schwerpunkte auch bei schlechten Werten noch gut zu tracken und trotzdem relativ schnell auf Änderungen zu reagieren, sodass das Filter nicht den Daten "hinterhängt":

  Q = 0.01*eye(4);
  R = 0.5*[ 10  0; 0 10 ];

Der Startwert kann nun geschätzt werden. Da keine Informationen darüber vorliegen wo die Schwerpunkte zu Beginn liegen, wurde dieser Vektor zu Null gewählt. Aufgrund der oben beschriebenen guten Reaktionsfähigkeit des Filters nähert sich dieses innerhalb weniger Zyklen den wahren Werten sehr gut an.

Maske Für das Auto

Durch die Position der Kamera auf dem Auto, ist ein Teil des Autos auch im Kamerabild sichtbar. Diese Informationen können sich im laufe der Bildverarbeitung als störend erweisen und ein Spur oder Start/Stopp Linien erkennen erschweren. Um eine Fehlinterpretation der Daten zu verhindern und die Spur oder Start/Stopp Linien Erkennung zu erleichtern ist es Sinnvoll diese Bildinformationen zu entfernen. Ein Ansatz der in Matlab bereits erfolgreich getestet wurde ist das Verwenden einer passenden Maske. Eine Binärmatrix die im Bereich des Autos mit Nullen und sonst mit Einsen besetzt ist und die Dimension der Bild Matrix besitzt. Nach einer Multiplikation der Matrizen sind alle Bildinformationen über das Auto entfernt.

Kamerabild, Maske, Kamerabild mit Maske

Inverse Perspective Mapping

Bei der Verwendung einer Kamera zur Fahrspurerkennung ergibt sich immer das Problem der perspektischen Verzerrung. Grund dafür ist, dass bei der Projektion aus dem 3D-Weltkoordinatensystem in das 2D-Koordinatensystem des Bildes Information verloren gehen. Das Inverse Perspective Mapping (IPM) bietet eine Möglichkeit die verloren gegangenen Daten zu rekonstruieren und das Bild in entzerrter Vogelperspektive darzustellen.

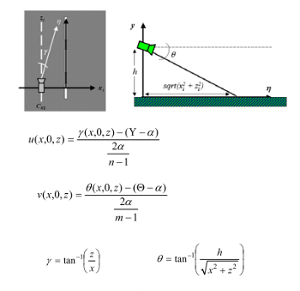
Dabei wird das Bild unter Verwendung von geometrischen Beziehungen aus dem Weltkoodinatensystem W = {(x,y,z)} in ein volgelperspektivisches Bild I = {(u,v)} transformiert. Dabei ist die die y-Komponente, wie auch in der Abbildung zu sehen ist, stets 0. Das liegt daran das eindeutige Zuordnung der Punkte nicht ohne Weiteres möglich, da schließlich Informationen verloren gegangen sind. Da hierbei Straßenlinien gefunden werden sollen, kann die Annahme getroffen, dass alle Punkte auf dem Boden und damit auf y = 0 liegen müssen. Im Fall nicht ebenen Straßen gilt diese Annahme nicht und fürht daher zu Fehlern. Das bedeutet, dass das IPM beispielsweise bei Straßen in Gebirgen nicht geeignet ist. Auch möglicherweise vor einem fahrende andere Fahrzeuge liegen nicht in der Bodenebene und sind in der Vogelperspektive verzerrt dargestellt. Der Abstand zu ihnen kann aber bestimmt werden. Außerdem müssen damit das IPM fehlerfrei funktioniert noch andere Anforderungen erfüllt sein. Position und Ausrichtung der Kamera müssen bekannt sein und es muss der Punkt auf dem Horizont fokussiert werden in dem sich die Fahrspuren zu schneiden scheinen, was wiederum erfordert, dass die Straße in der Mitte des Bildes liegt. Ist das nicht der Fall erhält man keine einwandfreien Ergebnisse, da die Straße immer noch eine perspektivische Verzerrung aufweist.

Ein Beispiel für gutes Ergebnis des IPM ist in Abbildung 1 zu sehen. [1]

Abbildung 1: Straße aus Vogelperspektive

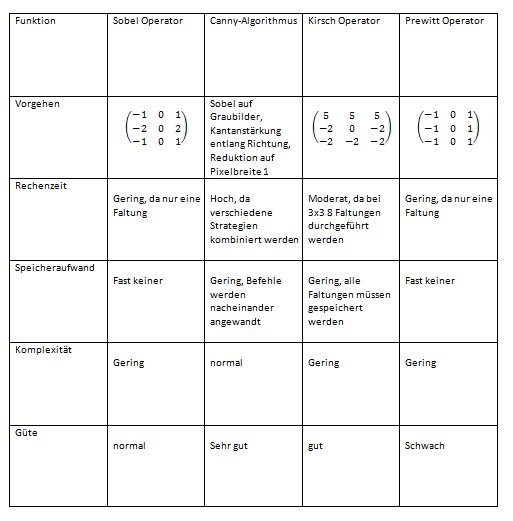
Operatoren zur Kantenerkennung im Vergleich

Quellen weiterführende Links

[1] SVN\SDE_Praktikum\Literatur\Inverse Perspective Transformation: ipm_paper_direkt
"Decomposing and composing a 3×3 rotation matrix" [1]
"Grundlegende mathematische Verfahren der 3D-Visualisierung"[2]
"Caltech Lane Detection Software"[3]
"Rekonstruktion 3D - Koordinaten aus Kamerabild"[4]

Fazit & Ausblick

Das Carolo-Cup Fahrzeug ist nun in der Lage die Fahrspur zu erkennen und ihr auch zu folgen. Dies funktioniert sowohl auf der Geraden als auch in Kurven relativ genau, wobei in Kurven noch stellenweise mit bis zu zwei Rädern die Spur leicht überfahren wird. Das Spurpolynom wurde von der rechten äußeren Fahrspur in die Mitte der Fahrbahn verlagert, sodass eine Regelung ohne weitere Umrechnung möglich ist. Außerdem können nun Stopplinien erkannt werden. Dabei stehen der Regelung ein Stoplinien-Bit und im Falle einer nahenden Stoplinie auch die Entfernung in Metern zur Verfügung. Mit dem vorbereiteten Ansatz zur Spurerkennung mit Hilfe des Kalman-Filters existieren auch Aufgaben die in folgenden Semesters aufgegriffen werden können. Damit lassen sich möglicherweise auch Schwächen des bisherigen Ergebnisses ausmerzen. Diese bestehen an der Kreuzung und in S-Kurven. Kreuzungen erfordern das überfahren einer Spurlinie. Diese darf dabei zu keinem Zeitpunkt als Spur erkannt und verfolgt werden. S-Kurven hingegen besitzen im Verlauf 2 lokale Extrema, die mit einem Polynom 2. Grades nicht abgebildet werden können. Ein Ansatz wäre hier einfach ein Polynom höheren Grades zu interpolieren. Dies würde aber zulasten der Rechenzeit pro Fram gehen und ist daher im Vorfeld abzuwägen.

Feedback zum Artikel

--Prof. Dr. Mirek Göbel (Diskussion) 13:54, 8. Aug. 2014 (CEST)

• Projektplan etc. nichts ins Wiki!
• Originaldaten der Bilder fehlen (zum ggf. Nacharbeiten)

Archiv bisheriger Arbeit

Objekterkennung mit Kamera

---

→ zurück zum Hauptartikel: Praktikum SDE