SoSe23 - Praktikum Systementwurf - Objekt- und Spurerkennung (OSE) mit Kamera

Abb. 1: Spurerkennung

Autor: Prof. Dr.-Ing. Schneider
Workshop 9: Objekt- und Spurerkennung (OSE) mit Kamera
Workshoptermin: 01.06.2023
Lernzielkontrolle 3: 22.06.2023

Einleitung

Die Workshops im SDE Praktikum sollen die Studierenden das praktische Arbeiten in einem Mechatroniklabor im Bereich modellbasierte Entwicklung mit MATLAB/Simulink und DSpace Hardware DS1104/ControlDesk vermitteln. Der Umgang soll in der Selbstlernzeit geübt werden.

Im Projekt OSE werden Objekte mit dem LiDAR-Sensor erkannt und verarbeitet sowie die Fahrspur mit der Kamera. Dieser Workshop fikussiert die Spurerkennung sowie die Bildung und den Transfer des Spurpolynoms an die DS1104.

Lernziele

Nach erfolgreicher Teilnahme am Workshop:

• können Sie die intrinsischen und extrinsischen Parameter einer Kamera bestimmen.
• können Sie eine Inverse Perspektiventransformation durchführen.
• können Sie Fahrbahnmarkierungen segmentieren.
• können Sie das Spurpolynom maßstabsgetreu bestimmen.
• können Sie das Spurpolynom via serieller Schnittstelle an die DS1104 senden und empfangen.

Bewertung

Die Bewertung erfolgt im Rahmen der Lernzielkontrolle 3.

Voraussetzungen

• Studieren Sie die Praktikumsordnung.
• Die unter Vorbereitung aufgeführten Aufgaben sind vor dem Workshoptermin vorzubereiten. Der Workshop baut auf Ihre Vorbereitung auf.

Ablauf des Praktikums

Tabelle 1: Agenda des Workshops

Uhrzeit	Agenda	Form
10:15	Begrüßung	Moderation durch Prof. Schneider
10:20	Bearbeitung der Aufgaben (vgl. Tabelle 2)	Gruppenarbeit
12:00	Statusbericht der Teams 1-6	max. 4 Min. pro Team
12:25	Verabschiedung	Moderation durch Prof. Schneider
12:30 Uhr	Veranstaltungsende

Vorbereitung

Aufgabe 9.1: Vorbereitung der Kamera

Abb. 2: MATLAB^® Camera Calibrator App

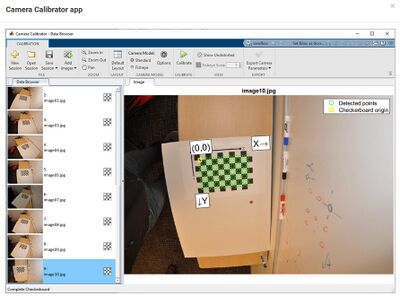
Um eine Kamera sinnvoll zur Spurerkennung einsetzen zu können, muss diese zuvor kalibriert werden.

1. Studieren Sie die zugehörigen Wiki-Artikel und arbeiten Sie sich in die Camera Calibrator App von MATLAB^® ein.
2. Führen Sie die Kamera-Kalibrierung mit MATLAB^® durch. Verwenden Sie hierzu eigene Bilder einer eigenen Kamera (möglichst mit Weitwinkellinse).
3. Identifizieren Sie extrinsische und intrinsische Parameter.
4. Machen Sie ein Foto eines vermessenen Aufbaus.
5. Transformieren Sie einen vermessenen Punkt von Weltkoordinaten in Bildkoordinaten und umgekehrt.
6. Dokumentieren Sie Ihren Versuchsaufbau, die Durchführung und Ergebnisse.

Links

• HSHL-Wiki: Kalibrierung_der_Kamera
• MATLAB^® Camera Calibrator App

Arbeitsergebnisse:

• Extrinsische Kameraparameter: $[x,y,z]_C, \Phi, \Theta, \Psi$
• Intrinsische Kameraparameter: k-Matrix
• kalibrierte Kamerabilder

---

Aufgabe 9.2: Segmentierung der Fahrbahnmarkierungen

Abb. 3: Segmentierung der Fahrspuren

1. Laden Sie das Video Rundkurs_IPT.mp4 aus dem Videoordner. Machen Sie keine Kopie.
2. Segmentieren Sie aus dem Kantenbild die 3 Fahrbahnmarkierungen
   1. rechter Fahrbahnrand (Gelb)
   2. Mittelspur (Rot) und
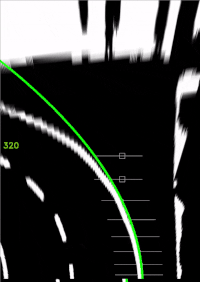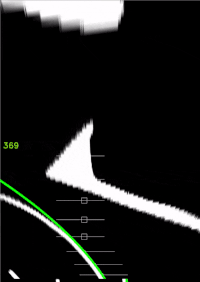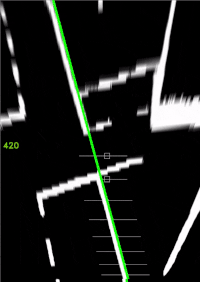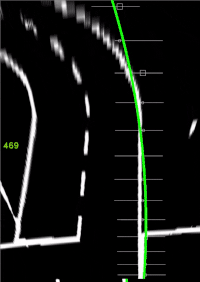
   3. linker Fahrbahnrand (Grün).
3. Zeigen Sie die Segmente farbig im Video an.

Eingangsdatei: SVN: Rundkurs_IPT.mp4

Arbeitsergebnis: X-Y-Daten der drei Fahrspuren für jeden Zyklus des Films segmentiereFahrbahnmarkierung.m

---

Aufgabe 9.3: Spurpolynom

Abb. 4: Darstellung der Fahrspuren als Polynom

1. Bestimmen Sie für die drei Spuren die Spurpolynome 2. Ordnung mit polyfit.
2. Ersetzen Sie polyfit durch die einfache Polynomapproximation interpoliere_weg.m.
3. Berechnen Sie aus dem Spurpolynom die drei Fahrspuren.
4. Blenden Sie die drei Fahrspuren im Videobild ein.

Demo: https://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/Software/Demos/Lane_Tracking

Arbeitsergebnis: Spurpolynome für jeden Zyklus des Films, Visuelle Überprüfung durch Einblendung in das Video zeigeSpurpolynom.m

Durchführung

Themen der Teams

Tabelle 2: Teameinteilung und Themen

#	Thema	Teilnehmer
1	9.4 Kamerakalibrierung	Oliver Scholze, Niklas Reeker
2	9.5 Inverse Perspektiventransformation (IPT)	Benjamin Dilly, Kevin Mudczinski
3	9.6 Referenzwerte	Xiangyao Liu, Yuhan Pan
4	9.7 Segmentierung der Fahrbahnmarkierungen	Johann Kismann, Dominik König
5	9.8 Spurpolynom	Louis Holtapel, Can Nen
6	9.9 Spurparameter (Empfangsseite)	David Weigt, Yunkai Lin

Aufgabe 9.4: Kamerakalibrierung

1. Messen Sie die extrinsische und intrinsische Parameter der Kamera mit der MATLAB^® Camera Calibrator App.
2. Machen Sie eine Aufzeichnung mit der Kamera von der Geraden bis in die erste Kurve. Steuern Sie den Wagen mit der Fernbedienung.
3. Geben Sie die validierten Parameter und das aufgezeichnete Video Spurerkennung.mp4 an Gruppe 2 weiter.
4. Vergleichen Sie Ihr Ergebnis mit der Dokumentation im HSHL-Wiki.
5. Stellen Sie Ihre extrinsische und intrinsische Parameter vor und diskutieren Sie diese.
6. Bewerten und verbessern Sie den Wiki-Artikels zur Kalibrierung der Kamera.

Arbeitsergebnisse:

• Versuchsprotokoll Kamerakalibrierung.docx
• Extrinsische und intrinsische Kameraparameter
• Video mit kalibrierter Kamera: Spurerkennung.mp4
• Wiki Artikel für die Kalibrierung extrinsischer und intrinsischer Kameraparameter

---

Aufgabe 9.5: Inverse Perspektiventransformation (IPT)

1. Studieren Sie den Artikel zur Inversen Perspektiventransformation mit MATLAB®.
2. Beschreiben Sie die Eingangsparameter. Nutzen Sie die Parameter von Gruppe 1.
3. Beschreiben Sie die Ausgangsparameter.
4. Wenden Sie die IPT auf das Video Rundkurs.mp4 an.
5. Bewerten Sie Ihr Ergebnis und aktualisieren Sie ggf. den Wiki-Artikel.
6. Konvertieren Sie mittels IPT das Video Spurerkennung.mpg.

Eingangsdateien: SVN: Rundkurs.mp4, Spurerkennung.mp4

Arbeitsergebnisse:

• Versuchsprotokoll InversePerspektiventransformation.docx
• Transformiertes Video Spurerkennung_IPT.mp4
• Dokumentation im Wiki (Verlinken Sie hier Ihr Ergebnis.)

---

Aufgaben 9.6: Referenzmessung

1. Bestimmen Sie die realen Spurparameter a, b, c für die Gerade.
2. Bestimmen Sie die realen Spurparameter a, b, c für die erste Linkskurve.

Arbeitsergebnisse:

• Versuchsprotokoll Referenzmessung.docx
• m-File zur Darstellung der Ergebnisse
• Ergebnisdatei Referenzmessung.mat
• Dokumentation im Wiki: Praktikum Systementwurf : Referenzmessung für das Spurpolynom

---

Aufgaben 9.7: Segmentierung der Fahrbahnmarkierungen

1. Segmentieren Sie die Fahrspuren aus dem Video Spurerkennung_IPT.mp4.
2. Segmentieren Sie aus dem Kantenbild die 3 Fahrbahnmarkierungen
   1. rechter Fahrbahnrand (Gelb)
   2. Mittelspur (Rot) und
   3. linker Fahrbahnrand (Grün).
3. Zeigen Sie die Segmente farbig im Video an.

Eingangsdateien: Spurerkennung_IPT.mp4

Arbeitsergebnisse:

• Versuchsprotokoll Segmentierung_der_Fahrbahnmarkierungen.docx
• X-Y-Daten der drei Fahrspuren für jeden Zyklus des Films segmentiereFahrbahnmarkierung.m als Fahrbahnsegmente.mat

---

Aufgaben 9.8: Spurpolynom

1. Bestimmen Sie für die drei Spuren die Spurpolynome 2. Ordnung mit interpoliere_weg.m.
2. Berechnen Sie aus dem Spurpolynom die drei Fahrspuren metrisch im Fahrzeugkoordinatensystem.
3. Blenden Sie die drei Fahrspuren im Videobild ein.

Eingangsdateien: Spurerkennung_IPT.mp4

Arbeitsergebnisse:

• Spurpolynome für jeden Zyklus des Films, Visuelle Überprüfung durch Einblendung in das Video zeigeSpurpolynom.m
• Versuchsprotokoll Spurpolynom.docx
• Spurpolynom als Spurpolynom.mat
• Dokumentation im Wiki (Verlinken Sie hier Ihr Ergebnis.)

---

Aufgaben 9.9: Spurparameter (Sende-/Empfangsseite)

1. Nutzen Sie die Spurerkennung auf dem Fahrzeug. Betrachten Sie die Gerade und die erste Kurve.
2. Vergleichen Sie die Spurparameter der Sendeseite mit der Referenz Referenzmessung.docx.
3. Vergleichen Sie die Spurparameter der Empfangsseite mit der Referenz Referenzmessung.docx.
4. Analysieren Sie ggf. Abweichungen und korrigieren Sie diese.

Arbeitsergebnisse:

• Versuchsprotokoll Validierung_der_Spurparameter.docx
• Dokumentation im Wiki

Nützlicher Link

• Allgemeine Anforderungen an ein Versuchsprotokoll
• MATLAB^®-Skript, welches die Messung in eine Auswertedatei umwandelt: funktion_wandle_dspacemess_in_CCF_mess.m

---

→ zurück zum Hauptartikel: Praktikum SDE | SDE-Team 2023/24