Projekt 70c: Labyrinth SLAM mit EV3
Autoren: Christian Sievers, Florian Scharfenberg
Betreuer: Prof. Schneider
→ zurück zur Übersicht: WS 18/19: Angewandte Elektrotechnik (BSE)
Aufgabe
Ein EV3 Roboter soll den Ausgang aus einem Labyrinth finden
Erwartungen an die Projektlösung
- Aufbau des EV3 Roboters in Abstimmung mit Prof. Schneider
- Recherche SLAM
- Ortung und Navigation via US oder IR Sensor und Odometrie (SLAM)
- Inbetriebnahme mit Matlab/Simulink
- Realisierung der Flucht aus dem Labyrinth
- Stellen Sie die digitale Karte des Labyrinths dar.
- Machen Sie spektakuläre Videos, welche die Funktion visualisieren.
- Test und wiss. Dokumentation
- Live Vorführung während der Abschlusspräsentation
Einleitung
Im Rahmen des Praktikums der angewandten Elektrotechnik im Modul ingenieurwissenschaftliche Vertiefung II des Masterstudiengangs Business and Systems Engineering, soll in diesem Projekt ein EV3 Roboter den Ausgang aus einem Labyrinth finden. Hierfür soll sich ein Aufbau eines EV3-Roboters, bestehend aus Aktoren und Sensoren konzipiert und umgesetzt werden. Dieser Roboter soll mit Matlab/Simulink programmiert werden und mit einer vorher überlegten Strategie (SLAM) den Ausgang des Labyrinths finden, sowie eine digitale Karte des Labyrinths erstellen.
Projekt
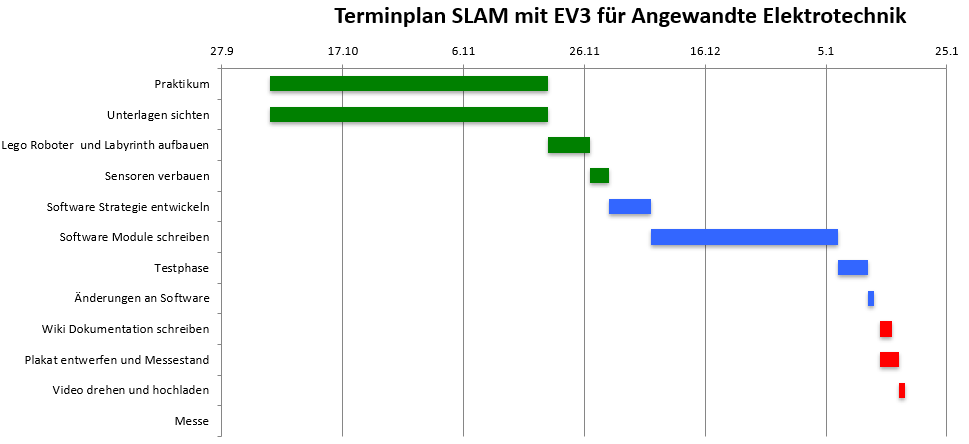
Projektplan
Um einen Überblick über das Thema zu erhalten, wurde die Zeitphase des Praktikums genutzt. Dabei wurden sowohl die bestehenden Unterlagen zum Thema SLAM mit Lego EV3 von vorherigen Projektteams gesichtet, als auch eigene Unterlagen. Geplant war mit dem Beginn der eigentlichen Arbeitspakete nach Ende der Praktikumsversuche. Dabei geht es sowohl um den mechanischen Aufbau, als auch der Programmierung des Roboters. Anschließend ist eine Testphase geplant gewesen, bei die Anforderungen schrittweise abgeprüft, Fehler dokumentiert und anschließend beseitigt werden sollten. Anschließend war die eigentliche Dokumentation, die Ausstattung des Messestands sowie die Videodokumentation geplant. Im Anschluss an alle Arbeitspakete steht der Meilenstein der HSHL Hausmesse am 18.01.2018.
Projektdurchführung
Konstruktion
Grundaufbau Robotor

Der Grundaufbau des Roboters stütz sich auf die Bauanleitung des Robot Educator des Robot Educator von Lego Mindstorms Education. Das Grundfahrgestell besteht aus dem EV3-Brick, zwei EV3 Motoren, die jeweils mit zwei Rädern verbunden sind und einer Metallkugel auf, die der hintere Teil des Roboters gestützt ist. Der Vorteil dieses Fahrgestells ist es, dass sich der Roboter durch die zwei einzelnen angetriebenen Räder und die unterstützende Metallkugel eine Drehung auf der Stelle realisieren kann und somit sein Bewegungsradius sehr gering ist.
.
Umbau auf 3 Ultraschallsensoren

Damit der Roboter sein Umfeld wahrnimmt wurden drei EV3 Ultraschallsensoren verwendet und in den Aufbau des Grundfahrgestells integriert. An den beiden Seiten sowie an der Front des Roboters wurde jeweils ein Ultraschallsensor angebracht. Unser Hauptprogramm ist aufgeteilt in 3 Unterprogramme die gleichzeitig ausgeführt werden. Diese Unterprogramme sind die Längsregelung, die Querregelung und die Ausführung der Kamera.
Optimierung Sensorpositionen
Wie in Abb.3 zu sehen ist, vergrößerte die Nachrüstung der seitlichen Ultraschallsensoren die Breite des Roboters. Nach ersten Versuchen der Bewegung des Roboters im Labyrinth fiel auf, dass die Ultraschallsensoren die Drehung des Roboters im Labyrinth erschweren. Für eine Drehung ohne dass der Roboter mit den Ultraschallsensoren die Wände streift, musste der Roboter perfekt in der Mitte platziert sein. Um dieses Problem zu lösen wurde an der Positionierung der seitlichen Ultraschallsensoren eine Optimierung durchgeführt.
Aufbau variables Labyrinth

Als Boden dienten für das Labyrinth, gleich große Holzplatten mit den Abmaßen 300x300mm. Aus 16 Holzplatte konnte so ein 4x4 Feld zusammengesteckt werden. Als Wände wurde Styruoduo verwendet, die mithilfe von Holzdübeln mit den Holzplatten verbunden wurden. Für die Versuche unseres Roboters aus dem Labyrinth zu entkommen entschieden wir uns für den Aufbau wie in Abbildung x zu sehen.
System Design
Toolbox Schnittstelle EV3
Software Matlab/Simulink
Matlab ist eine Software der Firma Mathworks zum Lösen von mathematischen Aufgaben. Die Hauptaufgabe ist dabei das berechnen und verarbeiten von Matritzen. Simulink ist eine grafische Umgebung, in der die in Matlab hinterlegten Funktionen verknüpft werden können. Wir haben in unserem Projekt ausschließlich in Matlab gearbeitet. Es gibt aber auch eine sehr gut funktionier ende Simulink Umgebung mit diversen Beispielen.
Toolbox Matlab EV3
Begonnen wurde das Projekt mit der integrierten Toolbox von Matlab. Diese Toolbox enthält einfache Befehle zur Ansteuerung von Sensoren und Motoren. Nach einiger Zeit hat sich aber herausgestellt, dass die Updaterate, mit der der EV3 Messwerte an Matlab liefert, so geringt ist, dass keine vernünftige Regelung erstellt werden kann. Durch die Messung im Sekundentakt werden sehr häufig Werte überfahren. Dadurch kann nicht sichergestellt werden, dass der Roboter passend anhält, nicht zu weit dreht und nicht gegen die Wand fährt. Um dieses Problem zu beheben, wurde auf die RWTH EV3 Toolbox gewechselt.
Toolbox RWTH EV3
Die RWTH EV3 Toolbox wird nicht mehr über die offizielle RWTH Mindstorm Internetseite verteilt, sondern ist auf Github zu finden. Die Installation wird in der beiliegenden Dokumentation beschrieben und ist schnell gemacht. Die Toolbox erlaubt eine Vielzahl von Sensoren auszulesen, sowohl EV3 als auch NXT. Für die Motorsteuerung gibt es einige zusätzliche Befehle wie die synchrone Zusammenarbeit oder die integrierte Regelung auf Zeit oder Schritte.
EV3
Connect
Mit dem Befehl connect wird eine Verbindung zum EV3 hergestellt. Die RWTH Toolbox unterstützt USB und Bluetooth Verbindung, wobei die Bluetooth Verbindung nicht hergestellt wurde. Dies kann laut Dokumentation am geänderten Bluetooth Treiber für Win10 liegen.
Um eine USB Verbindung aufzubauen benötigt man den folgenden Befehl:
b.connect('bt', 'serPort', '/dev/rfcomm0');
serPort muss der Serielle Port der Bluetoothverbindung angegeben werden. Diesen findet man in den Systemeinstellungen für den Bluetooth Adapter, der im Einsatz ist.
Für eine USB Verbindung:
b.connect('usb', 'beep', 'on', )
beep on sorgt für einen kurzen Ton wenn der EV3 verbunden ist.
Playtone
Mit playTone kann ein Ton über den Soundchip des EV3 abgespielt werden
myev3.playTone(10,1000,150)
Der erste Parameter ist die Lautstärke von 0 bis 100%
Der zweite Parameter ist die Freuqenz in Hz
Der dritte ist die Dauer in ms
Ultraschallsensoren
Der Primärsensor und seine Funktionen (Auszug aus Wiki Artikel Objekterkennung mit rotierenden Ultraschall mit Matlab/Simulink und EV3[1])

Der Sensor für dieses Projekt ist der LEGO Mindstorms EV3 Ultrasonic Sensor (95652) [1]. In Abbildung 1 wird der Sensor dargestellt. Er misst Entfernungen zwischen 3 und 250 cm. Die Messgenauigkeit liegt bei ± 1 cm. Der Sensor leuchtet dauerhaft beim Senden und blinkt beim Empfangen. Die EV3-Software erkennt den angeschlossenen Sensor automatisch und durch das passende Matlab/Simulink Supportpackage kann so auf den Sensor zugegriffen werden. Kurzgefasst besteht der Ultrasonic Sensor aus einem Sender und einem Empfänger. Der Sender emittiert die Ultraschallwellen, während der Empfänger die Ultraschallwellen empfängt. So können Objekte und deren Entfernung in cm gemessen werden. Der Ultrasonic misst die Strecke, indem er die Zeit auswertet die er benötigt, um die Ultraschallwellen auszusenden und wieder zu empfangen. [2]
Der LEGO Mindstorms EV3 Ultrasonic Sensor (95652) besteht unter anderem aus: [3]
- einem STM8S103F3 Mikrocontroller
- einem AW8T40-10OA00 Sender
- einem AW8R40-10OA00 Empfänger
Der Sender und der Empfänger besitzen folgende technische Daten: [4]
| Eigenschaft | AW8T40-10OA00 Sender | AW8R40-10OA00 Empfänger |
|---|---|---|
| Mittelfrequenz | 40.0±1.0KHz | |
| Schalldruckpegel | ≥110dB | - |
| Empfindlichkeit | - | ≥-67dB |
| Strahlungswinkel | 100° | |
| Kapazität | 1700±20%pF | |
| Gehäuse | Aluminum | |
| Max. Ansteuerungsspannung | 30Vrms | |
| Arbeitstemperatur | -20 bis +70℃ | |
| Lagertemperatur | -30 bis +80℃ | |
Messfehler
Die Werte der Ultraschallsensoren sind abhängig von diversen Störfaktoren:
- Da die Zeit gemessen wird, zwischen Senden und Empfangen können Störungen in der Elektronik zu verfälschten Werten führen
- Da das Ausbreitungsmedium Luft ist, hat die Umgebungstemperatur Einfluss auf das Ergebnis. Der Sensor ist kalibriert auf 20° Umgebungstemperatur laut Datenblatt.
- Die reflektierende Oberfläche hat starken Einfluss auf das Messergebnis. Da wir bei unserem Labyrinth immer die gleiche Oberfläche haben, kann man davon ausgehen, das dort keine großen Unregelmäßigkeiten auftreten.
- Der Analog- zu Digitalwandler bewirkt eine Quantisierung des Signals. Unser benötigte Messgenauigkeit ist aber um das 10-fache niedriger als die mögliche Ausgabe.
Durch Versuche hat sich herausgestellt, das man mit einer Genauigkeit von +- 1mm rechnen kann. Unser Algorithmus benötigt eine Genauigkeit von +-3mm, wodurch die Störfaktoren erträglich für das System sind.
setProperties
Um den Ultraschallsensor auslesen zu können muss er zunächst über setProperties intiialisiert werden.
Myev3.sensor1.setProperties('mode', DeviceMode.UltraSonic.DistCM);
Dieser Befehl setzt den Sensor an Port 1 in den Modus Ultraschall. Dieser Sensor gibt dann den Wert in cm aus. Der Sensor kann auch wenn gewünscht in Zoll ausgeben (DeviceMode.UltraSonic.DistIn)
Es können eine Vielzahl von Sensoren mit dieser Toolbox genutzt werden, auch NXT Sensoren.
value
Der Befehl value übergibt den aktuellen Wert an Matlab.
lensor.sensor1.setProperties('mode', DeviceMode.UltraSonic.DistCM);
x = lsensor.value
Kalibrierung
Um zu ermitteln, wie groß der gemessene Wert vom wirklichen abweicht, wurde ein kleines Tool geschrieben, das den Roboter schrittweise fahren lässt und den Messwert mit der gefahrenen Distanz gegenüberstellt. Dies wurde für alle drei Sensoren durchgeführt:
-
Abb.8: Linker Sensor
-
Abb.9: Mittlerer Sensor
-
Abb.10: Rechter Sensor
Die Messungen wurden jede 3x widerholt. Dabei wurde festgestellt, das die Abweichungen im Bereich +- 0,3mm liegen. Dieser Wert ist deutlich genauer als benötigt. Deswegen wurden keine Kennlinien zum Ausgleich im Tool hinterlegt. Sollte eine hohe Genauigkeit der Messwerte erforderlich sein, können die aufgenommenen Werte als Kalibrierung verwendet werden.
Motoren
Der verwendete Roboter besitzt zwei Schrittmotoren, die einzeln oder synchron angesteuert werden können.
Inkrementalgeber
Der Motor besitzt einen Inkrementalgeber, der die Winkelveränderung vom Motor messen kann. Damit kann abgefragt werden, wie weit der Motor gefahren ist. Ein weiterer Vorteil ist dabei, dass auch bei erzwungener Bewegung der Weg genau erfasst werden kann. Dies kann der Fall sein, wenn der Roboter sich auf einer Schrägen Ebene bewegt und die Gewichtskraft Einfluss nimmt.
Der Inkrementalgeber kann zu jedem Zeitpunkt zurückgesetzt oder ausgelesen werden.
X = l.tachoCount
Hiermit wird der aktuelle Wert übergeben.
resetTachoCount(l);
Der Wert wird auf 0 zurückgesetzt.
Motor Initialisierung
l = myev3.motorB;
Hiermit wird der Variable l der Motor an Port B übergeben. Der EV3 hat vier Ports für Motorsteuerung.
Motor Geschwindigkeit
l.power = 20;
Hiermit wird die Motorgeschwindigkeit festgelegt. Erwartet wird ein Wert von 0 bis 100.
SyncedStart
l.syncedStart(r);
Hiermit werden beide Motoren gleichzeitig gestartet. In der Klammer muss definiert werden, welche Motor mitlaufen soll.
Stop
l.stop();
Der Stop befehl stoppt den Motor. Falls er vorher synchron lief, wird er auch synchron gestoppt.
Bluetooth, Wifi und USB Schnittstellen
Der EV3 besitzt eine USB Schnittstelle, eine Bluetooth Schnittstelle und mit einem zusätzlichen Adapter auch eine W-Lan Schnittstelle. Mit der alten Matlab Toolbox kam der folgende Adapter erfolgreich zum Einsatz:
EDIMAX EW-7811UN Wireless USB Adapter, 150 Mbit/s, IEEE802.11b/g/n
Mit der RWTH Aachen Toolbox ist leider nur USB und Bluetooth möglich. Die Bluetooth Schnittstelle hat bei unseren beiden Notebooks leider keine Verbindung aufgebaut. Wir vermuten das nur bestimmte Bluetooth USB Adapter kompatibel mit der Toolbox sind, da die Bluetooth Schnittstelle mit der LEGO Software funktioniert hat. Für unseren Einsatz haben wir die USB Schnittstelle verwendet und das Kabel per Hand mitgeführt. Das dem EV3 Education Kit beigelegte Kabel hat eine ausreichende Länge für die Größe des Labyrinths.
myev3 = EV3();
myev3.connect('usb', 'beep', 'on'); %
Die beiden Befehle erstellen das EV3 Objekt und verbinden es mit Matlab. Der Parameter beep = on lässt den EV3 bei Verbindung piepen.
Strategie
Slam
Der Begriff SLAM setzt sich zusammen aus den Begriffen „Simultaneous Localization and Mapping“. Auf Deutsch würde man vom „Simultanem Lokalisieren und Kartografieren“ sprechen. Diese beiden Begriffe Lokalisieren und Kartografieren sind die Grundprinzipien von SLAM. Mit Hilfe von Algorithmen versucht man eine Karte zu erstellen und sich in dieser Karte zu lokalisieren. Dabei wird oft von einem „Henne Ei Problem“ gesprochen, da es notwendig ist eine Karte zu besitzen, um sich zu lokalisieren und die Position benötigt wird, um eine Umfeldkarte zu erstellen (Burgart, 2018). Mit der SLAM Problematik beschäftigen sich Wissenschaftler seit 1985. Im Laufe der Zeit haben sich durch neue Erkenntnisse wie Kalman oder Partikel immer mehr Möglichkeiten für Strategien entwickelt. Dadurch hat sich ein breites Spektrum an SLAM Varianten wie Fast-Slam, Partikel-Slam, SEIF (Sparse Extended Information Filter) und weitere gebildet (Nüchter, 2009).
Lokalisieren mit SLAM
Beim SLAM Algorithmus verwendet man Wegpunkte. Der Roboter, der sich in seiner Umgebung zurechtfinden möchte, misst die Entfernung und den Winkel von Zielen, die ihn umgeben. Durch eine Vielzahl von Zielen kann er seine Position in einer im zur Verfügung gestellten Karte ermitteln. Dabei ist wichtig, dass die Informationen soweit ausreichend sind, dass die Position eindeutig festgelegt werden kann. In Abbildung 1 ist zu erkennen, dass der Roboter drei Ziele erkannt hat. In unserem Fall nutzt der Roboter immer die Mitte jedes Planquadrats als Referenz. Er beginnt von hier die Messung und Bewegung und nutzt in der Bewegung die Sensordaten, um möglichst genau den nächsten Wegpunkt anzufahren. Wenn dieser nach Schätzung erreicht ist, beginnt ein neuer SLAM Zyklus. Da zu diesem Zeitpunkt alle alten Daten nicht mehr weiter verwendet werden, spricht man von einem Online-Slam.
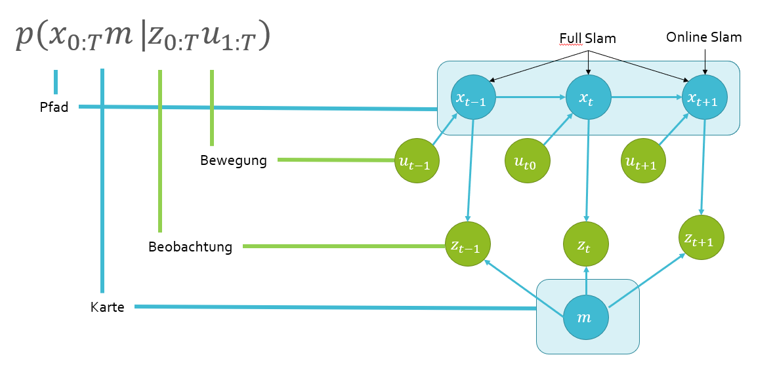
Die oben stehende Grafik wird typischerweise verwendet, um die Zusammenhänge zwischen den SLAM Daten zu beschreiben. Sie teilt die Daten in bekannte und unbekannte Daten. Die Bekannten Daten sind meine Bewegung und meine Beobachtungen die ich beim Start und bei jedem Schritt mache. Die unbekannten Daten sind die Karte und der Pfad den ich laufe. Der Pfad wird geschätzt abhängig von meinem bekannten Startpunkt und der Distanz die ich gefahren bin. Die Karte wird erzeugt durch die Vermutung, das ich mich wieder in der Mitte des Planquadrats befinde (Möglichst erreicht durch die Regelung der Motoren im Programmablauf) und den Sensormesswerten. Zur besseren Übersicht werden die Messwerte im Programm eingezeichnet und können damit mit den ermittelten Wänden verglichen werden.
Um den SLAM Algorithmus auf unser Problem anzupassen ist es hilfreich, ihn in Kategorien einzuteilen:
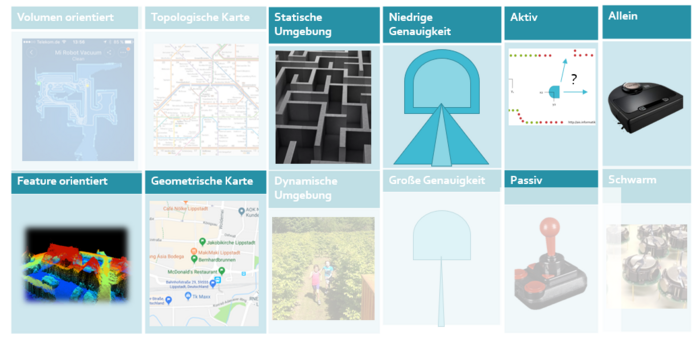
Volumen-orientiert/Feature-orientiert: Unser Roboter soll Wegpunkte und Messpunkte, sowie Wände einzeichnen, aber kein geschlossenes Volumen bilden. Deshalb spricht man von Feature-orientiert.
TopologischeKarte/Geometrische Karte: Unser Roboter trägt sowohl Pfade als auch Messwerte mit passender Skalierung in eine Karte ein. Deshalb spricht man von einer geometrischen Karte.
Statische Umgebung/Dynamische Umgebung: Der Roboter befindet sich ein einem Labyrinth in dem sich nichts dynamisch am Aufbau verändert und auch nichts sich dynamisch im Labyrinth bewegt. Zeitliche Veränderung spielt keine Rolle, deshalb spricht man von statischer Umgebung.
Niedrige Genauigkeit/Hohe Genauigkeit: Für den Algorithmus, den unser Roboter nutzt, sind niedrige Genauigkeiten notwendig, da er sich immer wieder an der Mitte orientiert und diesen über die Regelung der Motoren anfährt. Die Fehlerfortpflanzung über Wegpunkte wird damit vermieden.
Aktiv/Passiv: Der Roboter steuert sich selbst über die gemessenen Werte und wird nicht ferngesteuert. Deshalb spricht man von aktivem SLAM.
Allein/Schwarm: Der Roboter ist alleine und misst allein alle Werte.
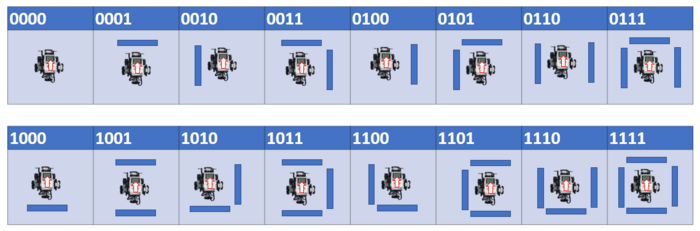
Strategie Labyrinth
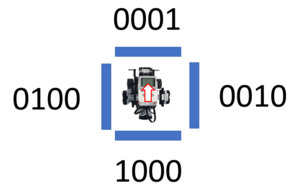
Der Roboter teilt das Labyrinth in gleich große Planquadrate von 32x32cm. Die Mitte der Planquadrate nutzt er als Anlauf- und Referenzpunkte. Dort fährt er Schritt für Schritt von Planquadrat zu Planquadrat. Er orientiert sich dabei immer an der rechten Wand (Siehe Rechte Hand Regel, folgender Abschnitt). Aus Sicht des Roboters gibt es 16 verschiedene Varianten, wie das Labyrinth ausgebildet werden kann. Dabei ist an den vier umliegenden Position jeweils eine Wand oder nicht (hinten-links-rechts-oben). Wenn eine Wand vorhanden ist, dann wird dies im Datensatz als 1 vermerkt. Da der Roboter immer direkt nach der Vorwärtsbewegung fährt, sind die 8 unteren Fälle nur möglich bei Beginn des Labyrinths. Um dort Fehler zu vermeiden, schaut der Roboter zu beginn nach vorne und falls sich dort eine Wand befindet dreht er sich einmalig um 90°. Danach ist sicher gestellt, das er nie durch seine Strategie in eine Wand fährt, es sei denn, er befindet sich in einem Quadrat mit 4 Wänden. Dies haben wir aber als Möglichkeit ausgeklammert, da wir nur von lösbaren Labyrinthen ausgehen.
Rechte Hand Regel
Die Rechte Hand Regel ist eine Strategie, bei der sich der Roboter immer an der rechts von ihm liegenden Wand orientiert und diese entlangfährt. Der Algorithmus geht davon aus, das die innenliegende Wand immer zum Ausgang führt. Dies ist auch gegeben, wenn der Anfang nicht an einer „Insel“ passiert. Dies ist ein eingeschlossener Bereich innerhalb des Labyrinths. Diesen würde man mit der rechten Hand Regel endlos umfahren, ohne den Ausgang zu erreichen.
Optimierung mit Inselerkennung - Pledge Algorithmus
Mit dem sogenannten Pledge-Algorithmus kann man das Problem der Inseln beheben. Dabei werden zwei Parameter betrachtet. Zum einen, wie viele Drehungen habe ich gemacht und zum anderen in welche Orientierung schaue ich gerade. Man definiert eine Richtung als sein Ziel (z.B. nach Norden ausgerichtet). Immer wenn wir nach Norden schauen, bewegen wir uns so lange bis wir wieder auf ein Hindernis treffen und nutzen dort erneut die rechte Hand Regel.
Logischer Aufbau mit 4 Ultraschallsensoren
Es wurde beim Aufbau mit 4 Ultraschallsensoren begonnen, da alle vier Wände erfasst werden sollen. Nach jedem Schritt prüft der Roboter in alle vier Richtungen, ob sich eine Wand befindet. Die gemessenen Werte werden über ein Median Filter angepasst, um Messfehler rauszufiltern.
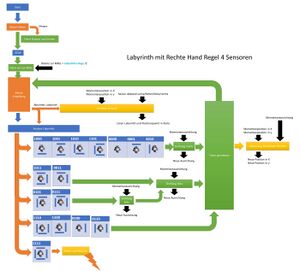
-
Logischer Aufbau mit 3 Ultraschallsensoren
Nach einigen Versuchen mit dem Labyrinth, ist ein Ultraschallsensor entfernt worden, da er nicht notwendig ist. Da man immer davon ausgehen kann, das nach jeder Bewegung hinter dem Roboter keine Wand ist, wird der Algorithmus vereinfacht mit 8 möglichen Labyrinth Varianten. Dies hat den Code deutlich vereinfacht, es ist nur der Startalgorithmus mit eventueller Drehung notwendig.
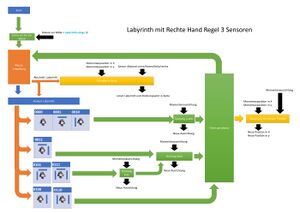
-
Filter (Kalman, Partikel)
Das Kalman Filter
Das Kalmanfilter ist ein Algorithmus der vom Mathematiker Rudolf Kálmán entwickelt wurde. Das Filter dient dazu den Zustand eines Systems anhand von Messwerten zu schätzen. Hierfür wird zu Beginn das Systemmodell in den Algorithmus implementiert sowie das System- und Messrauschen. Mithilfe der Messwerte macht das Kalmanfilter eine Vorhersage (Prädiktion) und vergleicht diese mit den neuen Messwerten.
Das Partikelfilter
Das Partikelfilter ist eine der Sequenziellen Mont-Carlo-Methoden und ist ein rekursiver Zustandsschätzer. Um eine Aussage über den Systemzustand zu treffen, werden zu Beginn eine ausgewählte Anzahl von Partikeln gleichmäßig über den gesamten Anwendungsraum gestreut. Im nächsten Schritt wird jeder Partikel mit der Messung des Systems, beispielsweise durch Sensoren, verglichen und je nach Übereinstimmung ein bestimmte Gewichtung zugeordnet. Durch einen sogenannten Resampling-Algorithmus werden die Partikel mit hoher Wahrscheinlichkeiten gefiltert. Im nächsten Zyklus werden die Partikel neu gestreut unter Berücksichtung der Positionen der Partikel mit hoher Wahrscheinlichkeit im vorherigen Zyklus. Die Zustandsschätzung mithilfe der Partikel wird solange ausgeführt bis im Idealfall alle Partikel sich auf eine Position befinden und die Aussage über den Systemzustand eindeutig ist.
Programmierung
Befehlsablauf
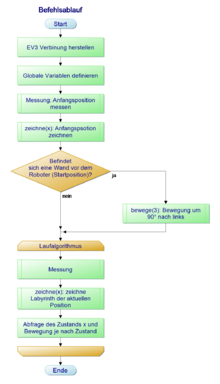
%****************************************************************
% Hochschule Hamm-Lippstadt *
%****************************************************************
% Modul : BSE Angewandte Elektrotechnik *
% *
% Datum : 15.12.2018 *
% *
% Funktion : EV3 durch HSHL Labyrinth schicken *
% *
% Implementation : MATLAB 2018b *
% *
% Toolbox : RWTH Aachen EV3 Toolbox *
% *
% Author : Florian Scharfenberg und Christian Sievers *
% *
% Bemerkung : *
% Letzte Änderung : 15.01.2019 *
% *
%***************************************************************/
% @Misc{rwthmindstormsev3toolbox,
% author = {Atorf, L. and Sondermann, B. and Stadtmann, T. and Rossmann, J.},
% title = {RWTH - Mindstorms EV3 Toolbox},
% year = {2018},
% version = {1.0},
% organization = {Institute for Man-Machine Interaction, RWTH Aachen University},
% url = {https://git.rwth-aachen.de/mindstorms/ev3-toolbox-matlab}
%% Vorherige Daten löschen und Verbindungen aufheben.
clear all;
clc;
%% Zugehörige Programmabschnitte:
% bewege.m Motorsteuerung
% Messung.m Labyrinth scannen mit Medianfilter und Messwerte analysiseren
% SchreibeMesswerte.m Werte speichern
% Umgebungston.m Messwerte als Ton ausgeben zur Analyse
% zeichne.m Übernimmt analysierte Wände in Karte
%% Verbinden des EV3
% Varianten der Kommunikation. Für RWTH wird die letzte Zeile eingesetzt.
% Momentan hat nur USB funktioniert mit RWTH.
% myev3 = legoev3('wifi','192.168.0.101','0016534341af');
% myev3 = legoev3('USB');
% Setup bluetooth connection via com-port 0
myev3 = EV3();
% Setup usb connection, beep when connection has been established b = EV3(); %
myev3.connect('usb', 'beep', 'on'); %
%% Globale Variablen definiert
global posx % Momentanposition in x
global posy % Momentanposition in y
global linex; %
global liney;
global richtung; % Gibt die Momentane Himmelsrichtung an, möglich ist N/E/S/W. Die Anfangsrichtung kann im Code verändert werden. Prinzipiell aber egal
global Anzahl; %Ein Zähler für die gemessenen Werte
global Messwertelinks; %Die Messwerte vom linken Ultraschallsensor
global Messwerterechts; %Die Messwerte vom rechten Ultraschallsensor
global wegstrecke; %Ein Arrey mit allen gefahrenen Positionen
global Messanzahl; %Ein kurzfristiger Zähler für die gemessenen Werte
global FahrDifferenz; %Die Distanz zum letzten als Richtig definierten Wegpunkt
global schrittzahl; %Ein Zähler für die gefahrenen Positionen
%% Initialisierungen
Anzahl = 1; %Anfang bei Wert 1
Messanzahl = 0;
posx = 0 %Startposition bei 0, kann frei gewählt werden
posy = 0 %Startposition bei 0, kann frei gewählt werden
plot(posx,posy,'p')
hold on
%Skalierung passend für das aktuelle Labyrinth, dies kann je nach Situation frei gewählt werden
xlim([-1900 900])
ylim([-400 1400])
richtung = 'E' %Die Startrichtung kann frei gewählt werden, hier passend zur Kameraperspektive. Muss nicht der echten Himmelsrichtung entsprechen
i=0; % Abbruchbedingung für while Schleife. Momentan nicht genutzt, könnte für Ausgang erkennung eingesetzt werden.
%% Anfangsposition prüfen ob vorne Wand
%Einfacher Start bei dem der Roboter schaut, ob vor ihm eine Wand ist.
%Falls eine Wand vorhanden ist, wird er nach rechts gedreht. So ist sicher
%gestellt, das der Programmablauf funktioniert und nur drei Ultraschall
%notwendig sind.
pause(0.2);
x = Messung(myev3); % Messung der aktuellen Position
zeichne(x);
if x(4)==1
bewege(3,myev3); % Drehung rechts 90°
end
%% Laufalgorithmus
% In der while Schleife wird zunächst geschaut, welche Wände vorhanden sind
% (links rechts vorne). Der Median Filter in dieser Messung filtert
% eventuelle Falschwerte heraus. Dann werden die Wände eingezeichnet und
% die Strategie gewählt. Je nach Fall wird gefahren, gedreht oder eine
% Kombination aus beidem.
while i == 0
pause(0.5);
x = Messung(myev3); % Messung der aktuellen Position
zeichne(x); % aktuelle Postion in Karte einzeichnen
% Abfrage des Zustandes für rechts Drehung und geradeaus fahren
if x(1)==0&&x(2)==0&&x(3)==0&&x(4)==1 ||x(1)==0&&x(2)==1&&x(3)==0&&x(4)==0 || x(1)==0&&x(2)==0&&x(3)==0&&x(4)==0 || x(1)==0&&x(2)==1&&x(3)==0&&x(4)==1
bewege(2,myev3); % Drehung rechts 90°
pause(1.5);
bewege(1,myev3); % Vorwärts 1 Abschnitt
end
% Abfrage des Zustands für eine links Drehung und geradeaus fahren
if x(1)==0&&x(2)==0&&x(3)==1&&x(4)==1
bewege(3,myev3); % Drehung links 90°
pause(1.5);
bewege(1,myev3); % Vorwärts 1 Abschnitt
end
% Abfrage des Zustands für zweifache links Drehung und geradeaus fahren
if x(1)==0&&x(2)==1&&x(3)==1&&x(4)==1
bewege(3,myev3); % Drehung links 90°
pause(1.5);
bewege(3,myev3); % Drehung links 90°
pause(1.5);
bewege(1,myev3); % Vorwärts 1 Abschnitt
end
% Abfrage des Zustands für geradeaus fahren
if x(1)==0&&x(2)==0&&x(3)==1&&x(4)==0 || x(1)==0&&x(2)==1&&x(3)==1&&x(4)==0
bewege(1,myev3); % Vorwärts 1 Abschnitt
end
end
Messung
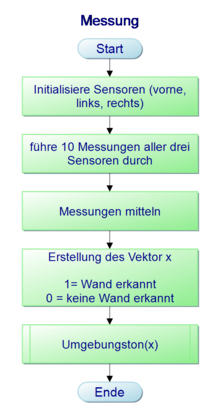
Die Funktion Messung ermittelt die Abstände der Wände links, rechts und vorne mit Hilfe eines Median-Filters. Wir haben im Testablauf gemerkt, das der Sensorwert sehr häufig richtig misst, nur in sehr seltenen Momenten starke Ausreißer bildet. Diese Ausreißer werden mit dem Median Filter herausgefiltert. An dieser Stelle wäre auch ein erweiterter Filter wie Partikelfilter und Kalman Filter möglich, um die Wände möglichst genau zu setzen. Für unseren Fall (gerade Wände und gleiche Längen) war dies allerdings nicht erforderlich. Die Ausgabe der Funktion ist eine Matrix, in der 0 für den Fall keine Wand und 1 für den Fall Wand geschrieben wird.
Die Reihenfolge ist: hinten - links - rechts - front
Hinten wird immer 0 geschrieben, da es im Programmablauf nur beim Start vorkommen kann, das eine Wand hinter uns steht. Dieser Fehler wird ausgeglichen indem beim Start geprüft wird ob vor uns eine Wand steht und wir in dem Fall uns um 90° drehen.
function x = Messung(myev3)
%% Messungen der Sensordaten
lsensor = myev3.sensor2;
rsensor = myev3.sensor3;
fsensor = myev3.sensor4;
lsensor.mode = DeviceMode.UltraSonic.DistCM;
rsensor.mode = DeviceMode.UltraSonic.DistCM;
fsensor.mode = DeviceMode.UltraSonic.DistCM;
for i=1:10
pause(0.2);
% db(i) = readDistance(bsensor)*100;
dl(i) = lsensor.value;
dr(i) = rsensor.value;
df(i) = fsensor.value;
end
%% Messungen mitteln
mdl = median(dl);
mdr = median(dr);
mdf = median(df);
%% Ausgabe des Umgebeungsvektor
x=zeros(4,1);
x(1)=0;
if mdl<20
x(2) = 1;
end
if mdr<20
x(3) = 1;
end
if mdf<20
x(4) = 1;
end
Umgebungston(x,myev3);
% clear myev3;
end
Umgebungston
Das Skript Umgebungston nimmt die vorab gemessenen Positionen der Wände links, rechts und vorne und lässt den Roboter schrittweise einen Ton für die einzelnen Position ausgeben. Bei einer Wand wird ein Ton mit 1000 Hz wiedergegeben, ohne Wand mit 500 Hz. Dies ist zwar nicht für den Programmablauf erforderlich, hilft aber der sofortigen Analyse im Testablauf. Dadurch können Fehler im Messen direkt erkannt werden und das Fehlverhalten vom Roboter genauer interpretiert werden.
Der Roboter piept in dieser Reihenfolge: hinten - links - rechts - vorne.
Hinten wird nie eine Wand angegeben, da das Skript so durchläuft, das hinter dem Roboter nie eine Wand ist beim messen.
%% Beepen des Roboters anhand des Umgebungsvektors
% Beep1: Hinten, Beep2: Links, Beep3: Rechts, Beep4: Vorne
function Umgebungston(x,myev3)
for i=1:4
pause(0.4);
if x(i)==0
myev3.playTone(10,1000,150)
else
myev3.playTone(10,500,150)
end
end
clear myev3;
end
Karte zeichnen
Die Funktion Karte zeichnen verwendet die in Messen ermittelte Matrix und schreibt damit die Wände in die Karte. Dabei wird von Fester Größe von 320mm ausgegangen. Dieser Wert kann für ein anderes Labyrinth angepasst werden oder mit Hilfe von anderen Strategien auch dynamisch geschrieben werden.
function zeichne(x)
% Die Funktion zeichnet die Wände in die Karte ein. Durch das vorhandene
% Labyrinth wird von geraden Wänden mit immer gleichen Längen ausgegangen.
global richtung;
global posx
global posy
global linex
global liney
global Anzahl
% Schreibe Oben
if (richtung=='N'&&x(4)==1)||(richtung=='E'&&x(2)==1)||(richtung=='W'&&x(3)==1)
linex(Anzahl,1) = posx-160;
linex(Anzahl,2) = posx+160;
liney(Anzahl,1) = posy+160;
liney(Anzahl,2) = posy+160;
plot([linex(Anzahl,1),linex(Anzahl,2)],[liney(Anzahl,1),liney(Anzahl,2)])
Anzahl = Anzahl +1;
end
% Schreibe Unten
if (richtung=='E'&&x(3)==1)||(richtung=='S'&&x(4)==1)||(richtung=='W'&&x(2)==1)
linex(Anzahl,1) = posx-160;
linex(Anzahl,2) = posx+160;
liney(Anzahl,1) = posy-160;
liney(Anzahl,2) = posy-160;
plot([linex(Anzahl,1),linex(Anzahl,2)],[liney(Anzahl,1),liney(Anzahl,2)])
Anzahl = Anzahl +1;
end
% Schreibe Links
if (richtung=='N'&&x(2)==1)||(richtung=='S'&&x(3)==1)||(richtung=='W'&&x(4)==1)
linex(Anzahl,1) = posx-160;
linex(Anzahl,2) = posx-160;
liney(Anzahl,1) = posy-160;
liney(Anzahl,2) = posy+160;
plot([linex(Anzahl,1),linex(Anzahl,2)],[liney(Anzahl,1),liney(Anzahl,2)])
Anzahl = Anzahl +1;
end
% Schreibe rechts
if (richtung=='N'&&x(3)==1)||(richtung=='E'&&x(4)==1)||(richtung=='S'&&x(2)==1)
linex(Anzahl,1) = posx+160;
linex(Anzahl,2) = posx+160;
liney(Anzahl,1) = posy-160;
liney(Anzahl,2) = posy+160;
plot([linex(Anzahl,1),linex(Anzahl,2)],[liney(Anzahl,1),liney(Anzahl,2)])
Anzahl = Anzahl +1;
end
end
Bewegung
function bewege(typ,myev3)
% Auswahl der Bewegung über Variable typ:
% 1 = geradeaus,
% 2 = Linksdrehung,
% 3 = Rechtsdrehung
%% Parameter für die Motoren
motordifferenz = 1.070; %Differenz für links und rechts, bei synchronem fahren nicht verwendet.
speed = 50; %Motorgeschwindigkeit
Daempfung = 5;
Reglung = 0.003; % Regelparameter für linkskurve und rechtskurve
%% Übernahme globale Variablen
global richtung
global posx
global posy
global linex;
global liney;
global Anzahl;
global Messwertelinks;
global Messwerterechts;
global wegstrecke;
global Messanzahl;
global FahrDifferenz;
global schrittzahl;
global Regelung;
%% Motor initialisierung
l = myev3.motorB; % Motor links
r = myev3.motorC; % Motor rechts
l.power = 20; % neu definieren der Geschwindigkeit für Motor links
%% Messungen der Sensordaten
lsensor = myev3.sensor2; %Ultraschall links an Port 2
rsensor = myev3.sensor3; %Ultraschall rechts an Port 3
fsensor = myev3.sensor4; % Ultraschall mitte an Port 4
% Einstellen der drei Sensoren auf Ultraschall Modus in cm
%(inch auch möglich falls gewünscht)
lsensor.mode = DeviceMode.UltraSonic.DistCM;
rsensor.mode = DeviceMode.UltraSonic.DistCM;
fsensor.mode = DeviceMode.UltraSonic.DistCM;
Bewegung nach vorne
Für die Bewegung nach vorne des Roboters wird die Information vom Inkrementalgeber verwendet. Dabei gibt es zwei Abbruchkriterien. Zum einen wird vorab ein fester Wert definiert, die der Roboter fahren darf bis zum nächsten Wegpunkt. Wenn der Wert vom Inkrementalgeber zurückgegeben wird, stoppt die Bewegung. Zudem wird permanent der Abstand nach vorne bestimmt. Wenn zwei mal der Sensorwert einen vorher bestimmten Fixwert unterschreitet, wird die Bewegung beendet. Parallel zur Bewegung durch die beiden Schrittmotoren, werden die Ultraschallsensoren links und rechts verwendet, um die Mauern um den Roboter in die Karte einzuzeichnen. Dabei wird nach jeder Messung eine kurze Pause von 0,2s gewartet, damit die Anzahl der Messwerte überschaubar bleibt. Dies ist aber frei änderbar. Die Messwerte werden in Matlab gespeichert und können nachträglich ausgewertet und weiterverarbeitet werden.
%% Vorwärts bewegen
if typ == 1
Fahrweg = 340; %war 320, etwas überfahren, da der Abstand nach Vorne überprüft wird
Winkel = Fahrweg/0.377; % Umrechnung von Strecke in ° vom Motor
l.limitMode='Tacho'; % Der Motor fährt bis zu einem definierten Wert
resetTachoCount(l); %Inkrementalgeber auf 0 gesetzt
l.limitValue = Winkel; % Limit wird übergeben
l.syncedStart(r); % Motorstart
schrittzahl = 0; % Initialisierung der Schrittzahl auf 0
Abstandvorne = fsensor.value; % Erste Messung zur Front
while schrittzahl < (Winkel-1)
% So lange der gewünschte Wert noch nicht erreicht wird, schreiben die Ultraschallsensoren
% Je nach Himmelsrichtung müssen die Werte abhängig von der momentanen
% x-Position anders eingetragen werden. Die vier Fälle sind über Richtung
% abgefragt.
if richtung == 'E' % Nach Osten schauend
Messanzahl = Messanzahl + 1;
% Messen links
Messwertelinks(Messanzahl,1) = Messanzahl;
Messwertelinks(Messanzahl,2) = posx + l.tachoCount*0.322 - 40; % Aktuelle Position + Schrittweite Motor links(Umrechnung in mm) - Offset Mitte Roboter zum Sensor
Messwertelinks(Messanzahl,3) = posy + lsensor.value *10 +100; %Aktuelle Position + Sensormessung (in mm umgewandelt) + Offset zur Roboter Mitte
plot(Messwertelinks(Messanzahl,2),Messwertelinks(Messanzahl,3),'.');
% Messen rechts
Messwerterechts(Messanzahl,1) = Messanzahl;
Messwerterechts(Messanzahl,2) = posx + l.tachoCount*0.322 - 40; % Aktuelle Position + Schrittweite Motor links(Umrechnung in mm) - Offset Mitte Roboter zum Sensor
Messwerterechts(Messanzahl,3) = posy - rsensor.value *10 -100; %Aktuelle Position + Sensormessung (in mm umgewandelt) + Offset zur Roboter Mitte
plot(Messwerterechts(Messanzahl,2),Messwerterechts(Messanzahl,3),'.');
%Einzeichnen der Strecke
wegstrecke(Messanzahl,1) = Messanzahl;
wegstrecke(Messanzahl,2) = posx + l.tachoCount*0.322;
wegstrecke(Messanzahl,3) = posy;
plot(wegstrecke(Messanzahl,2),wegstrecke(Messanzahl,3),'b--o');% Weg einzeichnen
elseif richtung == 'W' % Nach Westen schauend
% Messen links
Messanzahl = Messanzahl + 1;
Messwertelinks(Messanzahl,1) = Messanzahl;
Messwertelinks(Messanzahl,2) = posx - l.tachoCount*0.322 + 40; % Aktuelle Position + Schrittweite Motor links(Umrechnung in mm) - Offset Mitte Roboter zum Sensor
Messwertelinks(Messanzahl,3) = posy - lsensor.value *10 -100; %Aktuelle Position + Sensormessung (in mm umgewandelt) + Offset zur Roboter Mitte
plot(Messwertelinks(Messanzahl,2),Messwertelinks(Messanzahl,3),'.');
% Messen rechts
Messwerterechts(Messanzahl,1) = Messanzahl;
Messwerterechts(Messanzahl,2) = posx - l.tachoCount*0.322 + 40; % Aktuelle Position + Schrittweite Motor links(Umrechnung in mm) - Offset Mitte Roboter zum Sensor
Messwerterechts(Messanzahl,3) = posy + rsensor.value *10 +100; %Aktuelle Position + Sensormessung (in mm umgewandelt) + Offset zur Roboter Mitte
plot(Messwerterechts(Messanzahl,2),Messwerterechts(Messanzahl,3),'.');
%Einzeichnen der Strecke
wegstrecke(Messanzahl,1) = Messanzahl;
wegstrecke(Messanzahl,2) = posx - l.tachoCount*0.322;
wegstrecke(Messanzahl,3) = posy;
plot(wegstrecke(Messanzahl,2),wegstrecke(Messanzahl,3),'b--o');% Weg einzeichnen
elseif richtung == 'N' % Nach Norden schauend
Messanzahl = Messanzahl + 1;
% Messen links
Messwertelinks(Messanzahl,1) = Messanzahl;
Messwertelinks(Messanzahl,3) = posy + l.tachoCount*0.322 - 40; % Aktuelle Position + Schrittweite Motor links(Umrechnung in mm) - Offset Mitte Roboter zum Sensor
Messwertelinks(Messanzahl,2) = posx - lsensor.value *10 -100; %Aktuelle Position + Sensormessung (in mm umgewandelt) + Offset zur Roboter Mitte
plot(Messwertelinks(Messanzahl,2),Messwertelinks(Messanzahl,3),'.');
% Messen rechts
Messwerterechts(Messanzahl,1) = Messanzahl;
Messwerterechts(Messanzahl,3) = posy + l.tachoCount*0.322 - 40; % Aktuelle Position + Schrittweite Motor links(Umrechnung in mm) - Offset Mitte Roboter zum Sensor
Messwerterechts(Messanzahl,2) = posx + rsensor.value *10 +100; %Aktuelle Position + Sensormessung (in mm umgewandelt) + Offset zur Roboter Mitte
plot(Messwerterechts(Messanzahl,2),Messwerterechts(Messanzahl,3),'.');
%Einzeichnen der Strecke
wegstrecke(Messanzahl,1) = Messanzahl;
wegstrecke(Messanzahl,2) = posx;
wegstrecke(Messanzahl,3) = posy + l.tachoCount*0.322;
plot(wegstrecke(Messanzahl,2),wegstrecke(Messanzahl,3),'b--o');% Weg einzeichnen
elseif richtung == 'S' % Nach Süden schauend
Messanzahl = Messanzahl + 1;
% Messen links
Messwertelinks(Messanzahl,1) = Messanzahl;
Messwertelinks(Messanzahl,3) = posy - l.tachoCount*0.322 + 40; % Aktuelle Position + Schrittweite Motor links(Umrechnung in mm) - Offset Mitte Roboter zum Sensor
Messwertelinks(Messanzahl,2) = posx + rsensor.value *10 +100; %Aktuelle Position + Sensormessung (in mm umgewandelt) + Offset zur Roboter Mitte
plot(Messwertelinks(Messanzahl,2),Messwertelinks(Messanzahl,3),'.');
% Messen rechts
Messwerterechts(Messanzahl,1) = Messanzahl;
Messwerterechts(Messanzahl,3) = posy - l.tachoCount*0.322 + 40; % Aktuelle Position + Schrittweite Motor links(Umrechnung in mm) - Offset Mitte Roboter zum Sensor
Messwerterechts(Messanzahl,2) = posx - rsensor.value *10 -100; %Aktuelle Position + Sensormessung (in mm umgewandelt) + Offset zur Roboter Mitte
plot(Messwerterechts(Messanzahl,2),Messwerterechts(Messanzahl,3),'.');
%Einzeichnen der Strecke
wegstrecke(Messanzahl,1) = Messanzahl;
wegstrecke(Messanzahl,2) = posx;
wegstrecke(Messanzahl,3) = posy - l.tachoCount*0.322;
plot(wegstrecke(Messanzahl,2),wegstrecke(Messanzahl,3),'b--o'); % Weg einzeichnen
end
pause(0.2); % Variable Pause zwischen zwei Messwerten, kann beliebig gewählt werden
schrittzahl = l.tachoCount;
Abstandvorne = fsensor.value
if Abstandvorne < 8 % Parameter Abstand nach vorne, kann angepasst werden
l.stop(); % Motor frühzeitig anhalten bei zu geringem Abstand
break; % while Schleife verlassen!
end
end
% Einzeichnen der neuen Position im Labyrinth. Neuer Referenzpunkt für Messung und Strategie
if richtung == 'E'
posx = posx+320;
elseif richtung == 'W'
posx = posx -320;
elseif richtung == 'N'
posy = posy +320;
elseif richtung == 'S'
posy = posy -320;
end
plot(posx,posy,'p') % Position als Stern
end
Drehung links und rechts
Die Drehung nach links und rechts wird analog zur Vorwärtsbewegung durchgeführt, allerdings wird der synchronen Bewegung der Sensoren ein Parameter gegeben, damit die Sensoren sich gegenläufig bewegen. Bei einem Parameterwert von 200 bzw. -200 drehen sich die beiden Sensoren bei gleicher Geschwindigkeit in unterschiedliche Richtungen. Das Abbruchkriterium für die Bewegung ist ein vorher festgelegter Wert, der über den Abstand der Räder, die Größe der Räder und dem Abstand der Kugel zu den beiden Rädern berechnet werden kann. Wir haben den Wert durch ausprobieren ermittelt. Wenn man die Genauigkeit der Drehung erhöhen möchte, kann zusätzlich ein Gyro Sensor verwendet werden. Dieser ist deutlich genauer, war aber leider im Magazin der Hochschule nicht vorhanden. Für das Labyrinth das wir verwendet haben, war die Genauigkeit aber ausreichend.
%% Rechtsdrehung
if typ == 2
Fahrweg = 90; % Kann angepasst werden, falls Drehung zu schwach oder zu stark. Besser mit Gyrosensor, momentan aber nicht vorhanden im Bestand.
Winkel = Fahrweg/0.377;
l.limitMode='Tacho';
resetTachoCount(l);
l.limitValue = Winkel;
l.syncedStart(r,'turnRatio',200);
% Ausrichtung anpassen auf neue Himmelsrichtung
if richtung == 'N'
richtung = 'E'
elseif richtung =='E'
richtung = 'S'
elseif richtung == 'S'
richtung ='W'
elseif richtung == 'W'
richtung = 'N'
end
end
%% Linksdrehung
if typ == 3
Fahrweg = 90; % Kann angepasst werden, falls Drehung zu schwach oder zu stark. Besser mit Gyrosensor, momentan aber nicht vorhanden im Bestand.
Winkel = Fahrweg/0.377;
l.limitMode='Tacho';
resetTachoCount(l);
l.limitValue = Winkel;
l.syncedStart(r,'turnRatio',-200);
% Ausrichtung anpassen auf neue Himmelsrichtung
if richtung == 'N'
richtung = 'W'
elseif richtung =='E'
richtung = 'N'
elseif richtung == 'S'
richtung ='E'
elseif richtung == 'W'
richtung = 'S'
end
end
Kalibrierbewegung
Um den gewünschten Abstand bei der Vorwärtsbewegung und den genauen Wert für die 90° Drehung herauszufinden, haben wir uns ein kleines Programm geschrieben, mit dem wir die Parameter schnell ändern und die Änderung prüfen können.
resetRotation(motorrechts)
resetRotation(motorlinks)
motorlinks.Speed = speed*motordifferenz;
motorrechts.Speed = speed;
Fahrweite = 300;
Winkelzahl = Fahrweite/0.377
i = 0;
j = 0;
while i == 0
j = j+1;
start(motorlinks);
start(motorrechts);
rotationlinks(j) = readRotation(motorlinks);
rotationrechts(j) = readRotation(motorrechts);
motorlinks.Speed = speed*motordifferenz;
motorrechts.Speed = speed;
if rotationrechts(j) > rotationlinks(j)
motordifferenz = motordifferenz + 0.005
end
if rotationrechts(j) < rotationlinks(j)
motordifferenz = motordifferenz - 0.005
end
motorwert(j) = motordifferenz;
zielwert = rotationlinks(j)*100/Winkelzahl
motorlinks.Speed = speed*motordifferenz-(zielwert/Daempfung);
motorrechts.Speed = speed-(zielwert/Daempfung);
if rotationlinks(j) > Winkelzahl
i = 1
stop(motorlinks);
stop(motorrechts);
rotationlinks(j) = readRotation(motorlinks)
rotationrechts(j) = readRotation(motorrechts)
end
end
Sensortest
Für die Kalibrierwerte der Ultraschallsensoren haben wir ein Script geschrieben, das den Roboter immer Schrittweise (5mm) fahren lässt und anschließend nach einer Pause von 1s den Wert in eine Tabelle schreibt. Dadurch kann die gemessene zur wirklichen Entfernung verglichen werden. Man stellt den Roboter einfach vor eine weiße Wand und startet das Skript. Man sollte nach den 40 Messwerten, die das Programm aufnimmt einmalig überprüfen ob der maximale Wert der X-Achse auch zum Abstand vom Roboter zur Wand passt. Sollte die Position abweichen, kann der Fahrparameter im Skript leicht geändert werden.
myev3 = legoev3('USB');
sensor = sonicSensor(myev3,2)
% Bsensor = sonicSensor(myev3,4)
figure
h = animatedline;
ax = gca;
ax.YGrid = 'on';
ax.YLim = [0 30];
i=0;
stop = false;
startTime = datetime('now');
while ~stop
i=i+1;
pause(0.01);
% Read current voltage value
d = readDistance(sensor)*100;
dd = double(d);
% Get current time
t = datetime('now') - startTime;
% Add points to animation
addpoints(h,datenum(t),dd)
% Update axes
ax.XLim = datenum([t-seconds(15) t]);
datetick('x','keeplimits')
drawnow
% Check stop condition
if i>= 10000
stop = true;
end
end
Ergebnis
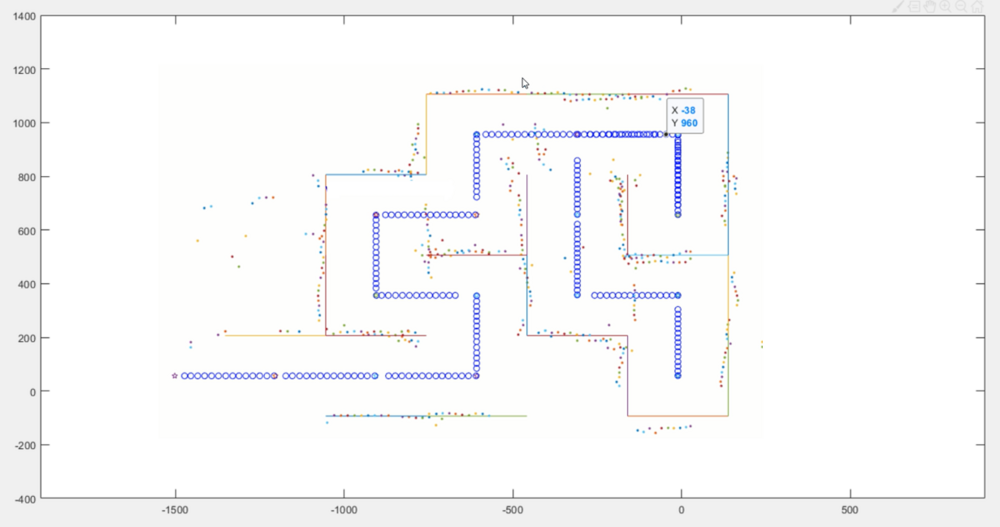
Das Ergebnis eines Labyrinth-Durchlauf ist in der folgenden Grafik zu sehen. Die Mauern werden als Linien und der Pfad des Roboters als Kreise dargestellt. Zusätzlich werden die von den Ultraschallsensoren gemessenen Daten mit geplottet. Der Aufbau entspricht dem von Abbildung 5.
Ein Vergleich der Sensordaten und der erstellten Karte mit der wirklichen Umgebung des Labyrinths ist in folgendem Bild erkennbar.
Die Wände liegen sehr gut über dem wirklichem Aufbau, nur einige Messwerte haben sich leicht verschoben.
Die erstellte Karte entspricht sehr genau dem verwendetem Labyrinth.
Erwartungen an die Projektlösung - Fazit
- Aufbau des EV3 Roboters in Abstimmung mit Prof. Schneider:
Der Lego Roboter ist nach dem Aufbau Plan des Lego EV3 Education Set durchgeführt worden. Die Abstimmung mit Prof. Schneider ist zu spät erfolgt um Änderungen vorzunehmen hat aber nicht zu Problemen geführt. Kleine Optimierungen vor allen in der Befestigung der Ultraschallsensoren sind nach einzelnen Testphasen durchgeführt worden.
- Recherche SLAM
Die Recherche SLAM ist im Zuge des Vortrags "Einführung in Slam" im Bachelor Mechatronik von Christian Sievers analog durchgeführt worden. Zusätzlich wurden weitere Informationen im Zuge der Vorlesung "Moderne Tracking Systeme" gesammelt.
- Ortung und Navigation via US oder IR Sensor und Odometrie (SLAM)
Der Sensor nutzt die drei Ultraschallsensoren um sich im Labyrinth zurecht zu finden. Da Anfangs Probleme mit der Samplingrate des EV3 bestand, wurde ein sehr vereinfachte Odemetrie verwendet. Dabei fährt der Roboter schrittweise die Mitte jedes Quadrats an. Für individuelle Labyrinthe mit krummen Wänden, unterschiedlichen Längen oder variablen Abständen müssen erweiterte Strategien wie Partikelfilter oder Kalmanfilter angewendet werden. Bei uns war der Median Filter ausreichend.
- Inbetriebnahme mit Matlab/Simulink
Der Ablauf ist komplett in Matlab realisiert worden.
- Realisierung der Flucht aus dem Labyrinth
Der Roboter erreicht selbstständig den Ausgang des Labyrinths.
- Stellen Sie die digitale Karte des Labyrinths dar.
Die Karte wird erfolgreich geschrieben und kann auch nach Beendigung betrachtet und weiterverarbeitet werden.
- Machen Sie spektakuläre Videos, welche die Funktion visualisieren.
Ein Video ist erstellt und in Youtube veröffentlicht.
- Test und wiss. Dokumentation
Der Roboter wurde mit diversen Labyrinthvarianten getestet und die Dokumentation im SVN und Wiki gepflegt.
- Live Vorführung während der Abschlusspräsentation
Die Live Präsentation ist am 18.01.2019.
Zusammenfassung
Um einen Überblick zu erhalten wurde am Anfang des Projekt ein Projektplan erstellt. Zu Beginn wurde der Mindstorms EV3-Roboter aufgebaut, sowie sich Gedanken über die Position der verbauten Sensoren gemacht. Gleichzeit wurde sich eine Variante eines Labyrinth überlegt und aus den variablen Holz und Styruoduo Modulen aufgebaut. Im Anschluss wurde der EV3-Roboter mithilfe von Matlab/Simunlink in Betrieb genommen. Zunächst wurden hiefür die Ansteuerung der Motoren und Erfassung der Daten der Ultraschallsensoren getestet. Mit einfachen Testprogrammen wurde die Bewegung des Roboters im Labyrinth getestet und die Sensorpositionen am Roboter optimiert. Die sich ausgedachte Strategie zum Entkommen des Roboters aus dem Labyrinth, wurde in einem Matlab-Programm, bestehend aus verschiedenen Funktionen implementiert. Durch verschiedene Tests und Anpassungen an der Programmierung, gelang es, dass der EV3-Roboter selbständig den Ausgang aus dem Labyrinth findet. Zu sehen ist dies im Youtubevideo.
Lessons Learned
Zum Abschluss des Projekts lässt sich sagen, dass die Projektplanung im Vorhinein förderlich für die Projektdurchführung war. Durch die Programmierung des EV3-Roboters und deren Aktoren und Sensoren wurden vertiefende Erfahrungen mit dem Umgang der Softwareumgebung Matlab/Simulink gesammelt, sowie der Datenerfassung von Sensoren. Bei der Programmierung fiel auf, dass die Kommunikation des EV3 mit Matlab/Simulink über unterschiedliche Toolboxen erfolgen kann. Einer möglichen nächsten Projektgruppe empfehlen wird die Programmierung mit der RWTH Mindstorms EV3 Matlab Toolbox.
Ausblick
Projektunterlagen
Die gewünschten Projektunterlagen befinden sich im SVN.
Diese sind unter diesem Link erreichbar: Link ins SVN
Dort ist die Zipdatei "Projektcode.zip" vorhanden. Falls keine Berechtigung besteht können Sie sich gerne an den betreuenden Professor Ulrich Schneider wenden.
YouTube Video
Youtube Video https://www.youtube.com/watch?v=mFR9on12qtw&t=7s[[2]]
Weblinks
Aufbauanleitung LEGO EV3 Education (17.01.2019 geprüft) https://education.lego.com/de-de/support/mindstorms-ev3/building-instructions[3]
LEGO MINDSTORMS EV3 Support from MATLAB (17.01.2019 geprüft) https://de.mathworks.com/hardware-support/lego-mindstorms-ev3-matlab.html[4]
Connect the Host Computer to an EV3 Brick Over a Wireless Network (17.01.2019 geprüft) https://de.mathworks.com/help/supportpkg/legomindstormsev3io/ug/connect-to-an-ev3-brick-over-wifi.html[5]
Wikipedia. (11. 12 2018). Simultaneous_Localization_and_Mapping . Von https://de.wikipedia.org/wiki/Simultaneous_Localization_and_Mapping abgerufen
Literatur
Burgart, W. (11. 12 2018). Robot Mapping - WS 2018/19 . Von http://ais.informatik.uni-freiburg.de/teaching/ws18/mapping/ abgerufen Doert, C. (11. 12 2018). Simultane Lokalisierung und Kartenerstellung eines autonomen Roboters. Von http://patrec.cs.tudortmund.de/pubs/theses/da_doert.pdf abgerufen
Markus Schoen, M. H. (11. 12 2018). Real Time Radar Slam. Von https://www.uni-das.de/images/pdf/veroeffentlichungen/2017/01.pdf abgerufen
Mathworks. (18. 12 2018). Implement Simultaneous Localization And Mapping (SLAM) with Lidar Scans. Von https://de.mathworks.com/help/robotics/examples/implement-slam-with-lidar-scans.html abgerufen
Nasa. (2018). Von https://mars.nasa.gov/resources/8819/mid-2017-map-of-nasas-curiosity-mars-rover-mission/ abgerufen
Nassour, D. J. (11. 12 2018). Vorlesungs Skript Robotik mit SLAM . Von SLAM https://www.tu-chemnitz.de/informatik/KI/edu/robotik/ws2012/robotik_9.pdf abgerufen
Nüchter, A. (2009). 3D Robotic Mapping: The Simultaneous Localization and Mapping Problem. Heidelberg: Springer.
researchgate.net. (11. 12 2018). Von : https://www.researchgate.net/publication/326429102 abgerufen
Quellenangaben Bilder
Zugehörige HSHL Wiki Artikel
Self Localization and Mapping (SLAM) mit Lidar- oder Kamera: http://193.175.248.52/wiki/index.php/Self_Localization_and_Mapping_(SLAM)_mit_Lidar-_oder_Kamera[6]
Einführung in SLAM – Simultaneous Localization and Mapping http://193.175.248.52/wiki/index.php/Einf%C3%BChrung_in_SLAM_%E2%80%93_Simultaneous_Localization_and_Mapping[7]
Lego Mindstorms EV3 http://193.175.248.52/wiki/index.php/Lego_Mindstorms_EV3[8]
Ultraschall mit Matlab/Simulink http://193.175.248.52/wiki/index.php/Ultraschall_mit_Matlab/Simulink[9]
Objekterkennung mit rotierenden Ultraschall mit Matlab/Simulink und EV3 http://193.175.248.52/wiki/index.php/Objekterkennung_mit_rotierenden_Ultraschall_mit_Matlab/Simulink_und_EV3[10]
--- → zurück zur Übersicht: WS 18/19: Angewandte Elektrotechnik (BSE)
- ↑ EV3 Ultraschallsensor: https://shop.lego.com/de-DE/EV3-Ultraschallsensor-45504, zuletzt abgerufen am 17.06.2017
- ↑ Erklärung Ultraschallsensor: http://gillespie.agrilife.org/files/2015/04/EV3-Motors-Sensors-Explained.pdf, zuletzt abgerufen am 17.06.2017
- ↑ Datasheet STM8S103F3: http://www.st.com/content/ccc/resource/technical/document/datasheet/ce/13/13/03/a9/a4/42/8f/CD00226640.pdf/files/CD00226640.pdf/jcr:content/translations/en.CD00226640.pdf, zuletzt abgerufen am 17.06.2017
- ↑ Datasheet Sender und Empfänger: http://www.quartz1.com/price/PIC/226N0120300.pdf, zuletzt abgerufen am 17.06.2017