Kalman-Filterung der Spurerkennung
Autoren: Jan Müller, Yannick Schmidt
Betreuer: Prof. Schneider
→ zurück zum Hauptartikel: OSE Softwareumgebung
→ zurück zum Hauptartikel: OSE - Objekt - und Spurerkennung
→ zurück zum Hauptartikel: Praktikum SDE
Einleitung

Der folgende Artikel beschreibt die Anwendung eines Kalman-Filters zur Filterung der Spurerkennung des Carolo-Cup-Fahrzeugs der HSHL. Hintergrund ist, dass der bisherige Algorithmus zur Spurerkennung keine Filterung beinhaltet und entsprechende Ausreißer, wie in Abbildung 1. zu sehen, zur Folge hat. Ziel der Integrierung eines Kalman-Filters ist die Eliminierung des in Abb. 1 zu sehenden Zappelns.
Hintergund Kalman-Filter
Die Anwendung des Kalman-Filters wurde im Verlauf der Lehrveranstaltung "Multisensorsysteme" erlernt. Der Kalman-Filter wird verwendet, um Parameter der verschiedensten Systeme zu schätzen. Er schätzt, basierend auf dem aktuellen und vergangenen Messwerten den Zustand des Systems und kann auf diese Weise Messungen eliminieren, die stark verrauscht sind. Der Filter setzt sich aus verschiedenen Parametern zusammen. Dazu gehört die Eingansgröße, Ausgangsgröße und das Systemmodell.
Auslegung des Kalman-Filters
Für eine optimale Filterung muss das Systemmodell passend ausgerichtet werden. Im folgenden wird die Bestimmung der wichtigsten Parameter (in Abbildung 2 zu sehen) aufgeschlüsselt.
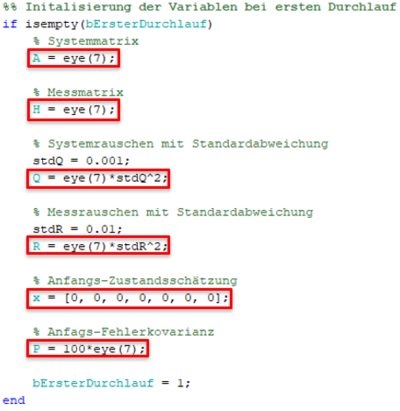
Systemmatrix A
Die Systemmatrix A wird als n*n Matrix angelegt. Wobei n aus der Länge des Messvektors ermittelt wird. Der Messvektor setzt sich im Falle der Spurerkennung aus insgesamt 7 Werten zusammen: 1-3. Die drei Werte des Polynoms (a, b, c), 4-5. x und y des ersten gefundenen Schnittpunktes, 6-7. x und y des letzten gefundenen Schnittpunkts. Auf diesen sieben Parametern basierend kann nun die Systemmatrix aufgestellt werden. Da es zwischen den Werten keine Abhängigkeiten gibt kann hier ganz einfach eine 7*7 Einheitsmatrix gebildet werden.
Systemrauschen Q
Das Systemrauschen Q wird über eine zuvor ermittelte Standardabweichung eingestellt welche mit einer 7*7 Einheitsmatrix multipliziert wird. Da unser aufgestelltes System nicht anfällig für Fehler ist haben wir uns hier für einen niedrigen Wert von 0.001 entschieden.
Messrauschen R
Ähnlich wie auch das Systemrauschen wird das Messrauschen basierend auf einer 7*7 Einheitsmatrix multipliziert mit einer zuvor bestimmten Standardabweichung bestimmt. Die Messungen weisen in der Regelung kein großes Rauschen auf, lediglich einzelne Frames beinhalten fehlerhafte Polynome. Aus diesem Grund haben wir uns hier für eine Standardabweichung von 0.01 entschieden.
Anfangs-Zustandsschätzung x
Hierbei handelt es sich um den ersten Messwert für den Kalman-Filter. Dieser muss das selbe Format haben wie der Messvektor. Der Einfachheit halber haben wir uns hier für einen 7*1 Nullvektor entschieden. Allerdings geben wir diesem Messwert im folgenden Messwert wenig Vertrauen, damit sich das Modell, basierend auf den folgenden Messwerten einpendeln kann
Anfangs-Fehlerkovarianz
Mit diesem Wert wird das Vertrauen für die erste Zustandsschätzung in dem Kalman-Filter integriert, je niedriger der Wert, desto höher das Vertrauen. Mit 100 haben wir das Vertrauen sehr gering eingestellt. Damit dem zuvor angelegten Nullvektor nicht groß vertraut wird.
Integrierung in Spurerkennung
Der Kalman-Filter wurde zuvor in der Matlab-Entwicklungsumgebung implementiert und ausgelegt. Anschließend wurde aus dem Matlab-Code c-Code, mithilfe des Matlab Coders generiert. Der generierte Code wurde anschließend in das Visual Studio Projekt integriert. Die Code-Generierung mit dem Matlab-Coder wird im folgenden Artikel genauer beschrieben: Von Matlab zu C code. Die generierte Funktion "KalmanFilter" wird anschließend in der Funktion der Spurerkennung, nachdem die Koordinaten transformiert wurden aufgerufen. Der folgende Auszug aus dem Quellcode der Spurerkennung zeigt den Umgang mit dem Kalman-Filter:
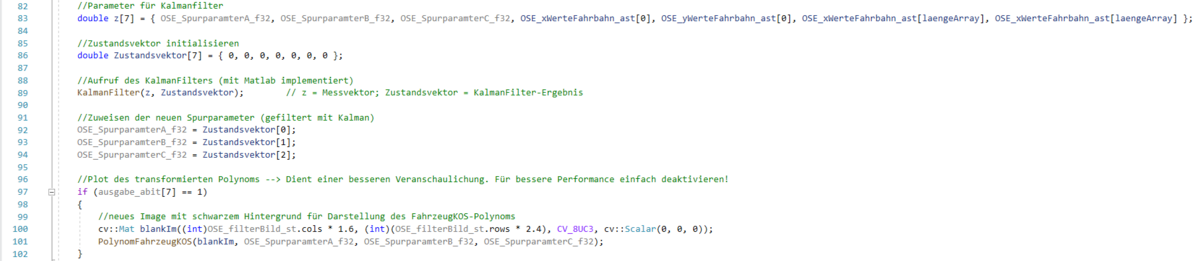
Dabei wird im ersten Schritt der Messvektor z aus Polynom-Parametern und Koordinaten generiert. Anschließend der Zustandsvektor für das Ergebnis der Filterung angelegt. Mit den beiden Vektoren kann nun der Kalman-Filter aufgerufen werden. Abschließend werden die Spurparameter mit den neuen Werten überschrieben und bei Bedarf in einem neuen Fenster (im Fahrzeug Koordinatensystem) ausgegeben (vgl. Abbildung 3).
Ergebnis

Mit der Anwendung des Kalman-Filters konnten die Ausreißer erfolgreich eliminiert werden. Die Abbildung 4 zeigt, dass das Polynom nun viel ruhiger verläuft und fehlerhaft erkannte Punkte nicht mehr zu unnötigem Rauschen des Polynoms führen. Dies hat zur Folge, dass die Regler weniger mit falschen Werten, bzw. starken Schwankungen zu kämpfen haben und die Spur generell zuverlässiger erkannt werden kann.
Lessons Learned
- Auslegung des Kalman-Filters
- Anwendung des Matlab Coders inkl. Einbindung in Visual Studio