AlphaBot: Messdatenverarbeitung mit MATLAB
| Autor: | Prof. Dr.-Ing. Schneider |
| Modul: | Praxismodul II |
| Lehrveranstaltung: | Mechatronik, Informatik Praktikum 2, 2. Semester |
Inhalt
- Einarbeitung in MATLAB®
- Programmierung und Anwendung eines gleitenden Mittelwertfilters
- Programmierung und Anwendung eines rekursiven Tiefpassfilters
- Auslegung von Filterparameter
- Anwendung der Filter auf eine Ultraschallmessung
- Vergleich der Filter anhand technischer Kriterien
Lernziele
Nach Durchführung dieser Lektion
- können Sie reale Messwerte speichern und via MATLAB® zyklisch visualisieren.
- haben Sie ein gleitendes Mittelwertfilter programmiert.
- haben Sie ein rekursives rekursiven Tiefpassfilter programmiert.
- können Sie die Filter parametrieren.
- haben Sie die Filter zyklisch auf Ultraschallmesswerte angewendet und das Filterverhalten analysiert.
- können Sie eine Funktion in MATLAB® programmieren und aufrufen.
Lernzielkontrolle
- Wozu werden rekursive Filter benötigt?
- Nennen Sie die Formel für ein gl. Mittelwertfilter.
- Welche Parameter hat ein gl. Mittelwertfilter? Was bedeuten die Parameter?
- Nennen Sie die rekursive Formel für ein Tiefpassfilter.
- Welche Parameter hat ein Tiefpassfilter? Was bedeuten die Parameter?
- Vergleichen Sie die zwei rekursiven Filter. Nennen Sie Vor- und Nachteile.
- Wurde der Quelltext durch Header und Kommentare aufgewertet?
- Wurde auf
magic numbersverzichtet? - Wurde die Programmierrichtlinie eingehalten?
Vorbereitung
Führen Sie als Vorbereitung den MATLAB® Onramp Kurs durch.
Arbeitsergebnis in SVN: MATLAB® Kurszertifikat
Versuchsdurchführung
Aufgabe 1.1: Positionserfassung mit Ultraschall
- Lesen Sie die Messwerte des Ultraschall-Sensors auf ein statisches Ziele aus. Schreiben Sie hierzu ein Arduino-Programm
messeEntfernung.ino. Messen Sie zyklisch die Zeit mit dem Befehlmillis(). - Messen Sie 10 s auf ein statisches Ziel (z. B. einen Karton) in 30 cm Entfernung.
- Nutzen Sie das Programm Putty, um die Daten der seriellen Schnittstelle in der ASCII-Datei
UltraschallMessung.txtzu speichern. Eine Anleitung finden Sie unter der URL Einrichtung von PuTTY. - Schreiben Sie einmalig als Header die Bezeichnung der Messwerte Zeit in ms und Strecke in cm in die Textdatei.
Nützliche Befehle: pinMode(), digitalWrite(), pulseIn(), delayMicroseconds(), millis()
Arbeitsergebnisse in SVN: UltraschallMessung.txt, messeEntfernung.ino
Tipp: Nutzen Sie das Demoprogramm DemoUltraschallHCSR04 als Programmierstart.
Aufgabe 1.2: Darstellung und Speicherung in MATLAB®
- Kopieren Sie das Demo
DemoDebugTxt2MATLAB.inoin Ihr Arbeitsverzeichnis und passen Sie es an. - Laden und visualisieren Sie die Messdaten in
Ultraschallmessung.txtmit MATLAB®. - Sichern Sie die Achsenbeschriftung im 2x1 Cell-Array
stTitel. - Stellen Sie die Messdaten in einem Diagramm in cm über der Zeit in s dar.
- Beschriften Sie die Graphen.
- Speichern Sie die Messung in der Datei
UltraschallMessung.mat.
Nützliche Befehle: plot, xlabel, ylabel, save
Arbeitsergebnisse in SVN: zeigeUltraschallMessung.m, UltraschallMessung.mat
Gegeben (vgl. Abb. 1):
fZeit: 1x100 Messwertarray der Zeit in sfMesswerte: 1x100 Messwertarray der Ultraschallwerte in cm
save('UltraschallMessung.mat','fZeit',fMesswerte','stTitel')
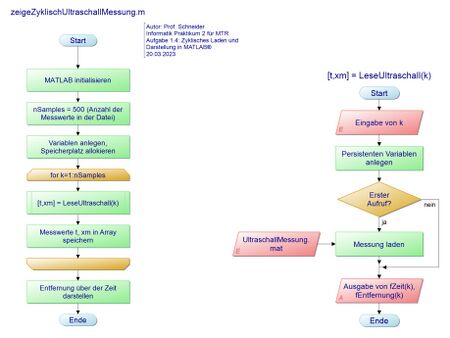
Aufgabe 1.3: Zyklische Messdatenverarbeitung in MATLAB®
- Schreiben Sie die Funktion
(fZeit, fEntfernung)=LeseUltraschall(k)und speichern Sie diese in der DateiLeseUltraschall.m. - Laden Sie darin
UltraschallMessung.mateinmalig nur bei ersten Durchlauf und speichern SiefZeit, fEntfernungals persistente Variablen. (fZeit, fEntfernung)=LeseUltraschall(k)gibt zwei Werte fZeit(k) und fEntfernung(k) zurück (z. B. [0 30] für 0 s und 30 m).- Schreiben Sie das Rahmenprogramm
zeigeZyklischUltraschallMessung.m, welchesLeseUltraschallzyklisch aufruft. - Stellen Sie im Rahmenprogramm die Messdaten in einem Diagramm in cm über der Zeit in s dar.
- Beschriften Sie den Graphen entsprechend Abb. 1.
Nützliche Befehle: plot, xlabel, ylabel, load, global, persistent, isempty, for, function
Arbeitsergebnisse in SVN: zeigeZyklischUltraschallMessung.m, LeseUltraschall.m
Aufgabe 1.4: Gleitendes Mittelwertfilter
Ein gleitendes Mittlwertfilter bildet einen Mittelwert über k Messwerte mittels FIFO.
- Schreiben Sie die Funktion
GleitendesMittelwertFilter.m, welches die Eingangswerte zyklisch filtert. Hier bei wird der Mittelwert über die letzten k Messwerte gebildet. - Testen Sie Ihre Funktion mit Ultraschallmesswerten mit statischen Zielen mit Ihrem Framework
zeigeZyklischUltraschallMessung.mundUltraschallMessung.matAus den Aufgaben 1.3 und 1.4. - Visualisieren Sie Messwerte und Filterergebnis in einem Plot mit Achsenbeschriftung und Legende.
- Testen Sie Ihre Funktion mit Ultraschallmesswerten mit dynamischen Zielen.
- Wählen Sie k anhand der Messwerte und diskutieren Sie Ihre Wahl mit Prof. Schneider.
Nützliche Befehle: plot, xlabel, ylabel, legend, persistent, isempty, isnan, function
Arbeitsergebnisse in SVN: GleitendesMittelwertFilter.m, testeGleitendesMittelwertFilter.m
Hinweise:
- Nutzen Sie ein Array als FIFO.
- Die Formel für das gleitende Mittelwertfilter lautet: für k Messwerte
| Einführung zu rekursiven Filtern |
Eine Einführung zu rekursiven Filtern finden Sie in folgendem Video.
|
| Demo |
|
SVN: DemoGleitenderMittelwert |
Aufgabe 1.5: Rekursives Tiefpassfilter
Ein rekursives Filter kann Messwerte in Echtzeit während der Laufzeit filtern. Nutzen Sie ein Tiefpassfilter, um die Messwerte zu filtern.
- Schreiben Sie die Funktion
TiefpassFilter.m, welches die Eingangswerte zyklisch filtert. Hierbei wird der Tiefpass berechnet. - Testen Sie Ihre Funktion mit Ultraschallmesswerten mit statischen Zielen mit Ihrem Framework
zeigeZyklischUltraschallMessung.mundUltraschallMessung.matAus den Aufgaben 1.3 und 1.4. - Visualisieren Sie Messwerte und Filterergebnis in einem Plot mit Achsenbeschriftung und Legende.
- Testen Sie Ihre Funktion mit Ultraschallmesswerten mit dynamischen Zielen.
- Wählen Sie anhand der Messwerte und diskutieren Sie Ihre Wahl mit Prof. Schneider.
Arbeitsergebnisse in SVN: TiefpassFilter.m, testeTiefpassFilter.m
Hinweis:
- Die Formel für das Tiefpassfilter lautet: für den aktuellen Messwert .
- ist hierbei ein Filterparameter .
| Demo |
| SVN: DemoTiefpassFilter.ino Eine ausführliche Beschreibung mit Musterlösung finden Sie in [1, S. 11 ff.19]. |
Aufgabe 1.6: Filtervergleich
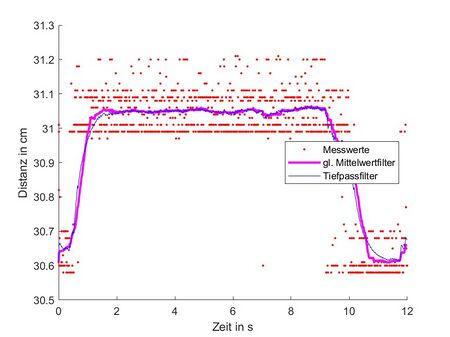
- Vergleichen Sie die Ergebnisse des Tiefpasses mit denen des gleitenden Mittelwertfilters.
- Zeigen Sie das ungefilterte und die gefilterten Signal in MATLAB® in einem Plot vergleichend an (vgl. Abb.1).
- Beschriften Sie die Achsen und nutzen Sie eine Legende.
Lernzielkontrollfragen:
- Wurde das Signalrauschen geglättet?
- Ist das gefilterte Signal verzögert?
- Welchen Einfluss haben die Filterparameter?
- Wie verhalten sich die gefilterten Signal bei Ausreißern?
Arbeitsergebnisse in SVN: testeFilterVergleich.m
| Musterlösung |
| Eine ausführliche Beschreibung mit Musterlösung finden Sie in [1, S. 27 ff.]. |
Tutorial zum Einstieg
- Was ist ein Plagiat?
- Einarbeitung in die Versionsverwaltung SVN
- Software Planung mit PAP
- Einstieg in die Welt des Arduino
- Einführung in MATLAB®
- MATLAB® Befehlsübersicht
- Einrichtung von PuTTY
- HSHL-Wiki: Ultraschallsensor HC-SR04
- Funduino: Entfernungen mit einem HC-SR04 Ultraschallsensor am Arduino messen
- Arduino Befehlsübersicht
- Programmierrichtlinie für C
- Programmierrichtlinien für MATLAB®
Demos
- SVN:
DemoUltraschallHCSR04 - SVN:
DemoDebugTxt2MATLAB - SVN: DemoUltraschallHCSR04
- SVN: DemoDebug2MATLAB
- SVN: DemoGleitenderMittelwert.ino
- SVN: DemoTiefpassFilter.ino
Literatur
- Kim, P.: Kalman-Filter für Einsteiger: mit MATLAB Beispielen. CreateSpace Independent Publishing: 2016. ISBN-13: 978-1502723789
- Schneider, U.: Programmierrichtlinie für für die Erstellung von Software in C. Lippstadt: 1. Auflage 2022. PDF-Dokument (212 kb)
FAQ
- Muss ich die Lösungen selbst programmieren? Ja, nur Eigenleistung wird bewertet.
- Darf ich die Musterlösung 1:1 kopieren und als meine Leistung ausgeben? Nein, das ist ein Plagiat und wird als Täuschungsversuch gewertet.
→ Termine 1 2 3 4 5 6 7 8 9 10 11
→ zurück zum Hauptartikel: Informatik Praktikum 2