Im Rahmen des Praktikums SDE, wurde das Teil-Projekt: AEP-Autonomes Einparken durchgeführt. In diesem Artikel, werden die Anforderungen an die Disziplin, die Auswahl der Sensoren, sowie verschiedene Grundlagen für den Einparkalgorithmus beschrieben. Die Autoren, die diesen Artikel verfasst haben sind: Sascha Dienwiebel, Martin Berysztak und Adem Hadziric.

Allgemeines

Anforderungen an die Disziplin

Die Anforderungen an das autonome Einparken in diesem Projekt wurden mit den Dozenten abgesprochen und richten sich teilweise an den Carolo Cup ^[1].

Das Fahrzeug muss auf einer geraden Straße - fahrend auf der rechten Straßenseite - eine passende Parklücke finden und in diese parallel zur Straße einparken.
Das Einparkmanöver muss durch einen Taster am Fahrzeug gestartet werden können.
Das Fahrzeug muss an rechts stehenden Hindernissen, auf der Suche nach einer ausreichend großen Parklücke, vorbeifahren.
Sobald die erstmögliche Parklücke gefunden ist, muss das Einparken mit dem rechten Blinker signalisiert werden.
Während des Einparkmanövers darf die äußere weiße Linie nicht überfahren werden.
Während des Einparkmanövers sind Kollisionen mit Hindernissen nicht erlaubt.
Der Abstand zum vorderen und hinteren Hindernis muss nach dem Einparkmanöver jeweils mindestens 0,1m betragen.
Nach Beendigung des Manövers muss das Fahrzeug zwischen zwei Hindernissen mit einer maximalen Winkelabweichung von 5° zum Stehen kommen. Zusätzlich müssen die Fahrtrichtungsanzeiger aufleuchten.
Das Einparkmanöver muss innerhalb von 30 Sekunden durchgeführt werden.

Autor: Sascha Dienwiebel (Diskussion) 18:23, 3. Feb. 2014 (CET)

Autor: Martin Berysztak (Diskussion) & Adem Hadziric (Diskussion) 14:39, 5. Feb. 2015 (CET)

Auswahl der Sensoren

Die Sensoren wurden in Anlehnung an gängige Lösungen des Carolo Cups ausgewählt. Für den Einparkvorgang werden vier Infrarotsensoren (nachfolgend: IR) vom Typ Sharp GP2D120, der Gierratensensor vom Typ LPR510AL und Hallsensoren zur Geschwindigkeitsermittlung verwendet.

Infrarotsensoren:

Die Positionen der IR sind im Artikel Sharp GP2D120 definiert und beschrieben. Der erste IR ist seitlich vorne am Fahrzeug montiert und wird dafür verwendet, die Parklücke zu finden und den Abstand zum seitlich parkenden Hindernis zu messen. Ein zweiter IR ist hinten-rechts auf höhe der Hinterachse angebrachte und misst ebenfalls den Abstand zu den Hindernissen, die die Parklücken darstellen. Mit Hilfe dieses Sensors wird bestimmt, wie weit das Fahrzeug an der gefundenen Lücke vorbeifahren muss, bis der Einparkvorgang gestartet wird. Die beiden anderen IR sind links und rechts an der Rückseite des Fahrzeugs angebracht und messen den Abstand zum hinteren Hindernis. Mit dieser Messung kann eine Kollisionserkennung implementiert werden und der tatsächliche Winkel des Fahrzeugs in der Parklücke bestimmt werden.

Gierratensensor:

Um die Winkellage des Fahrzeugs vermessen zu können, wird ein Gierratensensor verwendet. Die Änderung von Rechts- auf Linkseinschlag während des Einparkens wird durch eine vorher berechnete Winkellage β (siehe Berechnung nötiger Größen) gesteuert. Außerdem wird der Sensor dafür eingesetzt, das Anhalten des Fahrzeugs zu erreichen, sobald der Winkel des Gyroskops 0 rad (0°) erreicht.

Hallsensor (Geschwindigkeitsmessung):

Die Geschwindigkeit wird über Hallsensoren ermittelt. Über die Ableitung der Geschwindigkeit wird die Streckenmessung durchgeführt. Diese dient dem Zweck, die Parklücke zu vermessen und bestimmte Kurzstrecken, wie z.B. das Weiterfahren nach Lückenfindung, definiert zurückzulegen.

Autor: Sascha Dienwiebel (Diskussion) 18:23, 3. Feb. 2014 (CET)

Autor: Martin Berysztak (Diskussion) & Adem Hadziric (Diskussion) 14:39, 5. Feb. 2015 (CET)

Aktualisiert von Valentin Rentzsch 16:56, 23. Jun 2019 (CET)

Grundlagen

Einbindung des Einparkalgorithmus in die Simulink Umgebung

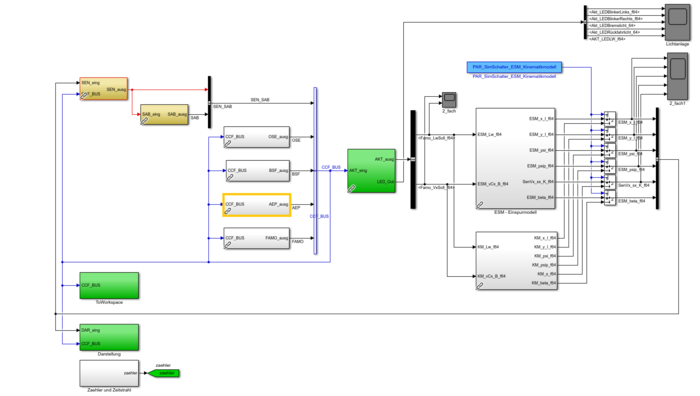
Das Hauptmodell für die Offline Simulation ist in der folgenden Abbildung dargestellt. Das Einparken wurde im Block AEP - Autonomes Einparken implementiert (orange hinterlegt dargestellt) und besitzt in der Online-Umgebung auf der Dspace Box denselben Aufbau, mit dem Unterschied, dass dort die Sensorwerte und Fahrbahn nicht simuliert werden müssen. Der gesamte Bus steht der Software zur Verfügung. Der Aufbau des Blocks und dessen internen Funktionen zur Umsetzung des Einparkalgorithmus findet sich in diesem Link wieder.

Autor: Sascha Dienwiebel (Diskussion) 18:24, 3. Feb. 2014 (CET)

Auswahl des Einparkmodus

Um das Einparkmanöver zu starten, muss zu Beginn das Simulink-Modell start.m Datei in MATLAB geöffnet werden. Für den Einparkmodus bestehen die Möglichkeiten, nach der Lückenfindung direkt einzuparken (Simulinkmodus = 3) oder stehen zu bleiben (Simulinkmodus = 2). Beim Online-Model muss beachtet werden, dass vor der Betätigung des AEP-Tasters, die Aktuatoren ausgeschaltet werden, damit die Kalibrierung des Gierratensensors gemacht wird. Hierzu muss der Hebel, der sich hinten am Fahrzeug befindet, in die Mittelstellung gebracht werden.

Alle weiteren Einstellungen sind optional und werden in diesem Link erläutert.

Autor: Sascha Dienwiebel (Diskussion) 18:24, 3. Feb. 2014 (CET)

Autor: Martin Berysztak (Diskussion) & Adem Hadziric (Diskussion) 14:39, 5. Feb. 2015 (CET)

Auswahl der geeigneten Geschwindigkeit

^[2]

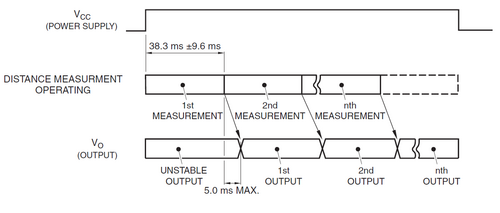
Der vorangegangenen Abbildung aus dem Datenblatt "Sharp-GP2D120.pdf"^[3] (siehe Infrarot Sensor) ist zu entnehmen, dass maximal eine Zeit für eine Messung benötigt wird, von:

$t= 38,3\,ms + 9,6\,ms + 5\,ms = 52,9\,ms$ .

Sicherheitshalber wird davon ausgegangen, dass sich in der größten Lücke ein weiteres Hindernis mit den Maßen 10cm x 10cm befindet. Um diese erkennen zu können, sollten mindestens drei Messungen im Bereich des Hindernisses stattfinden. Die benötigte Zeit für diese drei Messungen beträgt demnach:

$t=3\cdot 52,9\,ms = 158,7\,ms.$

Da sich die Geschwindigkeit aus dem Weg (s) geteilt durch die Zeit (t) berechnet und der Weg in diesem Fall der Länge des Hindernisses entspricht, resultiert daraus eine maximale Geschwindigkeit von:

$v= \frac{0,1\,m}{158,7\cdot10^{-3}\,s} =0,63\,\frac{m}{s}.$

Autor: Sascha Dienwiebel (Diskussion) 18:24, 3. Feb. 2014 (CET)

Autor: Martin Berysztak (Diskussion) & Adem Hadziric (Diskussion) 15:17, 5. Feb. 2015 (CET)

Aktualisiert von Valentin Rentzsch 16:56, 23. Jun 2019 (CET)

Berechnung nötiger Größen

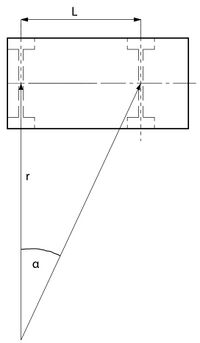
Das Fahrzeug besitzt einen maximalen Lenkeinschlag in eine Richtung von alpha = 23°. Kombiniert mit dem Radstand L = 0,265m ergibt dies einen Wendekreisradius um die Mitte der Hinterachse von:

$r= \frac{L}{tan(\alpha)} = \frac{0,265\,m}{tan(25^\circ)} = 0,5683\,m.$

Die folgende Abbildung zeigt eine Skizze zur Herleitung der Wendekreisradiusberechnung.

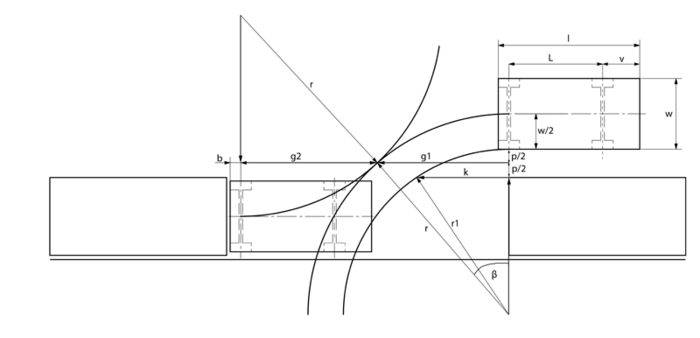
Für die Berechnung der notwendigen Parklücke spielt der Wendekreisradius (r), die Breite des Fahrzeuges (w), die Länge des Fahrzeugs von der Mitte der hiteren Achse bis zum Heck (b) und der seitliche Abstand zum Hindernis (p) eine wichtige Rolle. Die nachfolgende Abbildung zeigt eine Skizze des Fahrzeugs und dessen Einparkmanövers.

^[4]

Notwendige Größen für den Vorgang des Einparkens sind:

Die allgemeinen Maße des Fahrzeugs: Breite w = 0,290m; Radstand L = 0,265m; Abstand Mitte Vorderachse nach Vorne v = 0,065m; Abstand Mitte Hinterachse zum Heck b = 0,100m; Wendekreisradius r = 1,1318m
Der seitliche Abstand zum Hindernis p = variabel

Wird der Einparkvorgang gestartet, sobald die Mitte der Hinterachse des Fahrzeugs auf Höhe der Heckkante des vorderen Hindernisses liegt, müsste die Parklücke, wie der vorangegangenen Abbildung zu entnehmen ist, die Summe aus b, g1 und g2 sein. Die Abstände g1 und g2 sind dabei gleich groß und berechnen sich nach dem Satz des Pythagoras wie folgt:

$g1 = \sqrt[]{r^2-(r-\frac{w}{2}-\frac{p}{2})^2}$

Dies würde zu einer größeren Lücke führen, als eigentlich nötig, da die Möglichkeit besteht, nach Findung des vorderen Hindernisses eine weitere Strecke k nach vorne zu fahren. Dadurch wird gewährleistet, dass kein Platz verschenkt und während des Einparkvorgangs so nah wie möglich am Hindernis vorbeigefahren wird. Demnach wird für die Größe der nötigen Parklücke (g) folgende Formel verwendet:

$g = 2\cdot \sqrt[]{r^2-(r-\frac{w}{2}-\frac{p}{2})^2}+b-\sqrt[]{(r-\frac{w}{2})^2-(r-\frac{w}{2}-p)^2}$

Anhand dieser Formel wird deutlich, dass sich die nötige Parklücke danach richtet, wie groß der Abstand zum Hindernis ist. In der Regel ist der Abstand p nicht gleich 0. Dies würde bedeuten, dass das einparkende Fahrzeug bereits sich direkt am stehenden Fahrzeug befindet. Der Punkt, dass das Fahrzeug mittig der Straße fahren soll und die Tatsache, dass der Infrarotsensor erst ab einem Abstand von 4cm zuverlässige Werte zurückgibt (siehe GP2D120), setzt einen angenommenen Mindestabstand zur Berechnung voraus. In diesem Fall wird ein Abstand p = 15cm vorausgesetzt. Diese Annahme führt zu einer Mindestgröße der Parklücke von g = 1m. Durch geringe Vergrößerung des Abstandes p, Kürzung des Fahrzeugs oder Erhöhung des Einschlagwinkels würde auch eine kleinere Parklücke ausreichen. Der seitliche Abstand zum Hindernis darf allerdings nicht größer als die Hälfte des Wendekreisradius sein. Bei diesem Fall werden sämtliche oben genannten Berechnungen außer Kraft gesetzt.

Die Berechnung des Umschlagwinkels $\beta$ ist ebenfalls vom Abstand p abhängig und wird erst berechnet, wenn die Lücke gefunden und das Fahrzeug neben dem vorderen Hindernis steht.

$\beta = \arccos(\frac{r-\frac{w}{2}-\frac{p}{2}}{r})$

Ebenso wird an dieser Stelle der Weg berechnet, den das Fahrzeug noch vorwärts fahren soll, um den vorhandenen Platz so effizient wie möglich zu nutzen. Je näher beim Einparken an dem vorderen Hindernis vorbeigefahren wird, desto weniger Platz wird während des gesamten Einparkvorgangs benötigt. Da sich beim Finden des vorderen Hindernisses die Vorderachse des RC Fahrzeuges auf höhe dessen Hecks befindet und der Einparkvorgang so kalkuliert wird, dass sich erst mal die Mitte der Hinterachse des RC Fahrzeuges auf Höhe des Hecks des vorderen Fahrzeugs befindet, muss auf jeden Fall die Strecke der Summe aus Radstand (L) und Mitte der Hinterachse zur Front (v) gefahren werden. Auf diesen Wert wird dann noch der Parameter k addiert, welcher sich wie folgt berechnet und bereits Teil der Parklückenberechnung ist:

$k = \sqrt[]{(r-\frac{w}{2})^2-(r-\frac{w}{2}-p)^2}$

Da bei allen Parkmanövern (offline- und online-Modus), das Fahrzeug eine zu weite Strecke nach vorne gefahren ist, ist die benötigte Länge der Vorausfahrt reduziert worden. Hier ist über Tests rausgekommen, dass der Abzug der Größe k weggelassen werden kann.

Autor: Sascha Dienwiebel (Diskussion) 18:24, 3. Feb. 2014 (CET)

Autor: Martin Berysztak (Diskussion) & Adem Hadziric (Diskussion) 14:39, 5. Feb. 2015 (CET)

Test der Abstandssensorik

Autor: David Reger

Generierung von Testfällen

Um die Abstandssensorik zu testen werden Testfälle generiert und in Datenbanken gespeichert. Hierfür wurde in der Simulation eine Laufzeitvariable erstellt und an bestimmten Positionen die Simulation gestoppt. Die benötigten Variablen in den Testfällen sind folgende:

• ObjektListe
• Schalter
• stIRPosition
• x
• y
• psi

Zusätzlich ist zu beachten, dass die Simulation in der bibliothek 'SensorenAktoren_offline' gestoppt werden muss, da die Variablen nur lokal in der Funktion gespeichert werden und global nicht sichtbar sind. Damit Datenbanken in Matlab erstellt werden können muss der 'save' - Befehl verwendet werden. Jedoch hatte dieser in der Simulation einen Fehler ausgelöst, da dieser dort nicht verwendet werden darf. Um den Fehler zu umgehen wurden an den Stellen, an denen das Fahrzeug gestoppt werden sollte ein Breakpoint gesetzt. In einer if - Bedingung wurde bei Erreichen eines Wertes der Laufzeitvariable der Breakpoint gesetzt. Nun kann im Matlab Command Window der 'save' - Befehl manuell eingetippt werden.

Beispiel für die Erstellung einer Datenbank:

• save('Messung1.mat','ObjektListe','stIRPosition','x','y','psi')

Durch Eingabe der 'Enter' - Taste wird die Datenbank im Arbeitsordner angelegt. Weiterhin ist zu beachten, dass die Variablen nicht im Workspace angezeigt werden, aber vorhanden sind. Deshalb ist das Speichern der Variablen möglich.

Die Ergebnisse zu der Generierung von Testfällen befinden sich im Branch Einparksensorik_SS_19.

Auswertung der Sensordaten

Für die Auswertung gibt es eine Testumgebung für die Abstandssensorik. Diese befindet sich bei folgendem Link: GUI_Testumgebung Um die Datenbanken der generierten Testfälle in die Testumgebung einzubinden, müssen sie zuvor in den Ordner, in dem sich die Testumgebung befindet, eingefügt werden. Zusätzlich dazu müssen die Bilder in des Testfalls in den Ordner geladen werden, damit über die GUI der entsprechende Test ausgewählt werden kann.

Anschließend kann in Matlab durch Starten der GUI der gewünschte Testfall ausgelessen werden.

Nachdem die Datenbank in der Testumgebung eingelesen wurde, wird diese gestartet. Anschließend zeigt die GUI an, ob der Test bestanden (1) oder nicht bestanden (0) wurde.

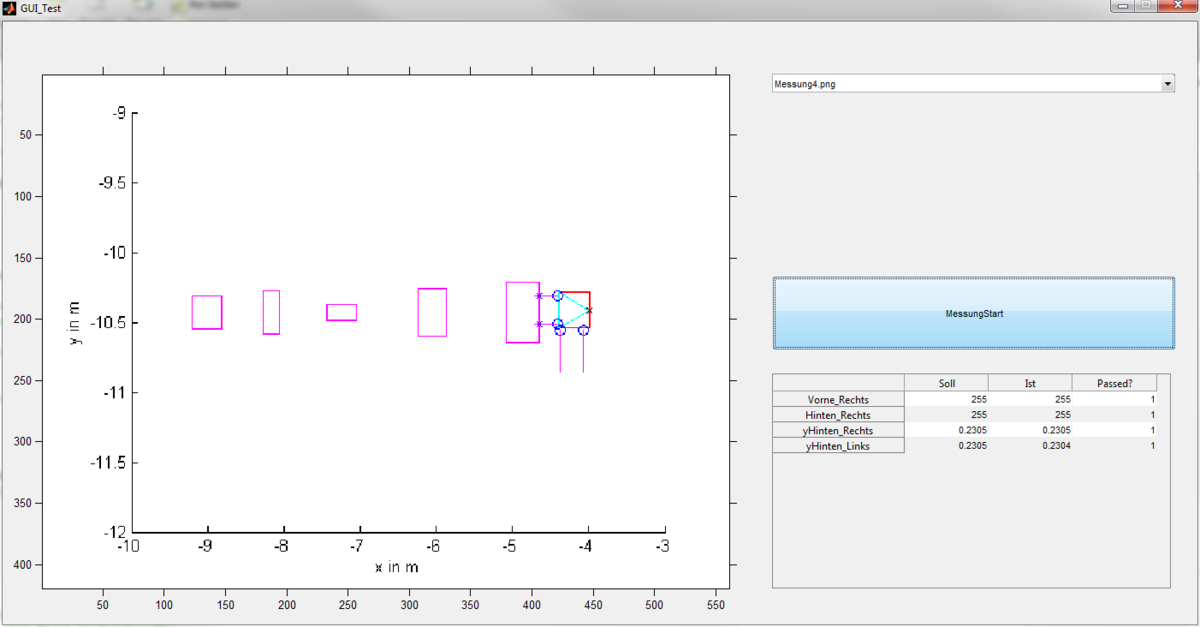
Über das DropDown-Menü "Auswahl des Testfalls" kann der jeweilige Testfall geladen werden. In dem Koordinatensystem wird dann optisch der Test dargestellt, damit der Anwender sieht welcher Test durchgeführt wird. Über den Button "MessungStart" wird die Messung durchgeführt. Hierfür wurde die Testumgebung als Funktion ausgelagert und in der GUI aufgerufen. In einer Tabelle werden dann alle notwendigen Testdaten angezeigt.

Das nachfolgende Beispiel zeigt den Testdurchlauf für den Fall "Messung4":

In der Tabelle können die vorgegebenen Soll-Werte abgelesen werden. Durch die berechneten Ist-Werte wird ermittelt, ob die Abweichung in Ordnung ist. Das Ergebnis wird in der letzten Spalte angegeben. Die GUI befindet sich im SVN.

Nach Durchführung aller Messungen stellte sich heraus, dass die hinteren Sensorwerte vertauscht sind.

Optimierung der Software zur Aufnahme von Messwerten

Autor: Yanick Christian Tchenko (Diskussion) - 03. 06. 2019

Die eben dargestellten in den Testfällen benötigten Variablen werden teilweise mittels einer im Programm implementierten Schleife automatisch generiert. Damit lassen sich weiterhin bei einer Geradefahrt die verschiedenen Hindernisse detektieren.
Die Änderung der Variable x von -10 bis -3 ermöglicht eine schrittweise Bewegung des in der Simulation modellierten Fahrzeugs. Am Ende jedes Schrittes wird der x- und der y-Wert des detektierten Hindernisses in einer Text-Datei gespeichert, welche bei jedem neuen Aufruf überschrieben wird.

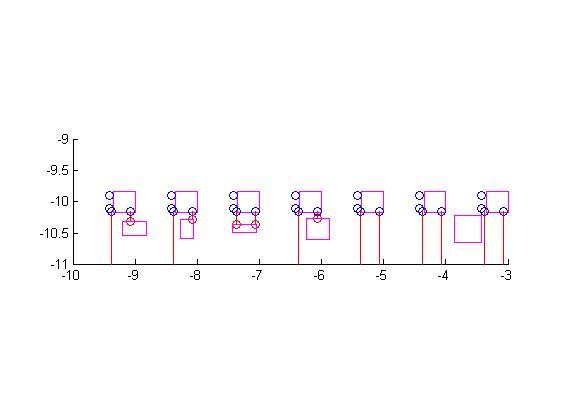
Beschleunigte Ermittlung von Sensormesswerten

Autor: Yanick Christian Tchenko (Diskussion) - 03. 06. 2019

MATLAB ist eine interpretierte Sprache. Dies bedeutet, dass jede Operation einen zusätzlichen Overhead in C oder C++ mit sich bringt. Diese Auswahl und Zuordnung der Matlab-Programmteile ist der Hauptgrund, warum MATLAB langsamer ist als kompilierte Sprachen. Der Overhead-Interpreter ist besonders wichtig, wenn Ihre Operationen mit Skalaren oder kleinen Datenmengen ausgeführt werden. Dies erklärt, warum skalarbasierte Schleifen in MATLAB notorisch langsam sind.
MATLAB enthält eine Just-in-Time-Codegenerierung (JIT) oder Mex-Umstellungsmöglicchkeit, mit der dieses Problem in begrenzten Fällen behoben werden kann. Die Mex-Umstellung ermöglicht es, einen effizienten Code in C zu schreiben bzw. zu generieren (mithilfe vom Codegenerator), ohne den ursprünglichen Matlab-Code zu verlieren.

Die Umsetzung dieser Technik zur Generierung der Mex-Funktion erfolgt durch folgenden Befehl:

 • t = coder.typeof(0, [1e6 3],1);<br>
 • C = coder.typeof(0, [1e6 3],1);<br>
 • vt = coder.typeof(0, [1e6 3],1);<br>
 • R = coder.typeof(0, [1e6 9],1);<br>
 • EV = coder.typeof(0, [1e6 3 3],1);<br>
 • '''codegen Matlab-Funktionsname -args { EV,t,vt,C,R }'''<br>

Der Einsatz im Rahmen des Simulationsprogramms zur Einparksensorik erfolgt durch den Befehl:

codegen fcn -args {zeros(1,1,'double'),zeros(1,1,'double'),zeros(1,1,'double'),zeros(5,8,'double'),zeros(4,2,'double'),zeros(1,1,'double')}

Dabei werden die Parameter entsprechend den Funktionsparamtern angepasst.

Nach Aufruf dieses Befehls in Matlab Command Windows kommt man im Projektordner auf eine generierte C-Version der berücksichtigten Matlab-Funktion. Diese C-Version wird automatisch mit folgendem Namen generiert: Matlab-Funktionsname_mex

Als nächstes wird im Hauptprogramm der Matlab-Funktionsname (fcn) durch den Namen der entsprechenden generierten Mex-Version (fcn_mex) ersetzt, wobei nach der Programmausführung die in der folgenden Tabelle dargestellten Laufzeitdifferenzen zu erkennen sind:

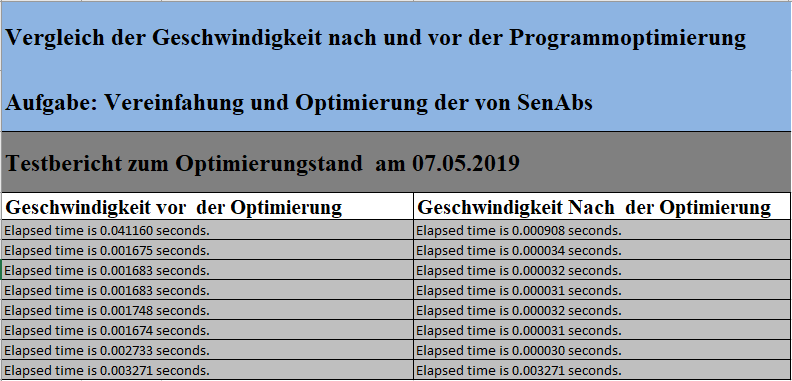
Aktueller Stand

Offline-Simulation

Das Fahrzeug startet nach einer kurzen Verzögerung zur Kalibrierung des Gierratensensors seine Fahrt entlang der Parklücken. Während des gesamten Suchvorgangs ist die geregelte Geradeausfahrt aktiv. Um dies zu zeigen startet das Fahrzeug im aktuellen Stand der Simulation leicht schräg und findet dann wieder auf seine Spur zurück. Nach dem es eine Parklücke gefunden hat, fährt es an dieser noch vorbei, bis die Hinterachse auf gleicher Höhe wie das Heck des vorderen Fahrzeugs der Parklücke ist. Nach dem Finden der Parklücke parkt das Fahrzeug ein und positioniert sich in der Parklücke. Alle Vorraussetzungen wurden erfüllt.

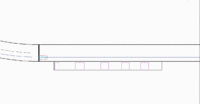
Online-Modell

Der aktuelle Softwarestand wurde bis jetzt noch nicht auf dem Fahrzeug getestet. Die Implementierung für das Online Modell steht für das WS 2019 an.

Autor: Valentin Rentzsch (Diskussion)

Lageregelung beim Einparken

Das Spezialthema soll zur Verbesserung der Ausrichtung des Fahrzeugs in der Parklücke beitragen. Aktuell befindet sich die Erweiterung aufgrund ausstehender Tests noch in einem SVN Branch.

Ausblick

Aufgrund des fehlerhaften Online-Modells ist die Betrachtung des Einparkmanövers nur in der Simulation und nicht am Fahrzeug möglich (siehe Starten der Online-Simulation).

Mögliche Erweiterungen des autonomen Einparkens sind folgende:

Verknüpfung mit der Regelung zur Geradeausfahrt (aktuell: Vorgabe eines 0° Lenkwinkels)
Lageregelung beim Einparken
Kollisionskontrolle

Autor: Steffen Topp (Diskussion)

Quellen / Weiterführende Literatur

↑ "Lastheft für das Projekt Autonomes Fahrzeug" von Prof. Dr. M. Göbel & Prof. Dr. U. Schneider, Hochschule Hamm-Lippstadt, Department Lippstadt.
↑ "Sharp-GP2D120" von Sharp, Sharp.
↑ "Sharp-GP2D120" von Sharp, Sharp.
↑ "Ein mathematisches Modell zum Parallelparken" von Nobert Herrmann, Univ. Hannover.

→ zurück zum Hauptartikel: Praktikum SDE

[1] "Lastheft für das Projekt Autonomes Fahrzeug" von Prof. Dr. M. Göbel & Prof. Dr. U. Schneider, Hochschule Hamm-Lippstadt, Department Lippstadt.

[2] "Sharp-GP2D120" von Sharp, Sharp.

[3] "Sharp-GP2D120" von Sharp, Sharp.

[4] "Ein mathematisches Modell zum Parallelparken" von Nobert Herrmann, Univ. Hannover.

[1]

[2]

[3]

[4]

AEP - Autonomes Einparken

Inhaltsverzeichnis

Allgemeines

Anforderungen an die Disziplin

Auswahl der Sensoren

Grundlagen

Einbindung des Einparkalgorithmus in die Simulink Umgebung

Auswahl des Einparkmodus

Auswahl der geeigneten Geschwindigkeit

Berechnung nötiger Größen

Test der Abstandssensorik

Generierung von Testfällen

Auswertung der Sensordaten

Optimierung der Software zur Aufnahme von Messwerten

Beschleunigte Ermittlung von Sensormesswerten

Aktueller Stand

Offline-Simulation

Online-Modell

Lageregelung beim Einparken

Ausblick

Quellen / Weiterführende Literatur

Navigationsmenü