AEP - Autonomes Einparken

Einleitung

Im Rahmen des Praktikums SDE, wurde das Teil-Projekt: AEP-Autonomes Einparken durchgeführt. In diesem Artikel, werden die Anforderungen an die Disziplin, die Auswahl der Sensoren, sowie verschiedene Berechnungen für den AEP - Autonomes Einparken beschrieben. Die Autoren, die diesen Artikel verfasst haben sind: Sascha Dienwiebel, Martin Berysztak und Adem Hadziric.

Allgemeines

Anforderungen an die Disziplin

Die Anforderungen an das autonome Einparken in diesem Projekt wurden mit den Dozenten abgesprochen und richten sich teilweise an den Carolo Cup .

1. Das Fahrzeug muss auf einer geraden Straße - fahrend auf der rechten Straßenseite - eine passende Parklücke finden und in diese parallel zur Straße einparken.
2. Das Einparkmanöver muss durch einen Taster am Fahrzeug gestartet werden können.
3. Das Fahrzeug muss an rechts stehenden Hindernissen, auf der Suche nach einer ausreichend großen Parklücke, vorbeifahren.
4. Sobald die erstmögliche Parklücke gefunden ist, muss das Einparken mit dem rechten Blinker signalisiert werden.
5. Während des Einparkmanövers darf die äußere weiße Linie nicht überfahren werden.
6. Während des Einparkmanövers sind Kollisionen mit Hindernissen nicht erlaubt.
7. Der Abstand zum vorderen und hinteren Hindernis muss nach dem Einparkmanöver jeweils mindestens 0,1m betragen.
8. Nach Beendigung des Manövers muss das Fahrzeug zwischen zwei Hindernissen mit einer maximalen Winkelabweichung von 5° zum Stehen kommen. Zusätzlich müssen die Fahrtrichtungsanzeiger aufleuchten.
9. Das Einparkmanöver muss innerhalb von 30 Sekunden durchgeführt werden.

Autor: Sascha Dienwiebel (Diskussion) 18:23, 3. Feb. 2014 (CET)

Autor: Martin Berysztak (Diskussion) & Adem Hadziric (Diskussion) 14:39, 5. Feb. 2015 (CET)

Auswahl der Sensoren

Die Sensoren wurden in Anlehnung an gängige Lösungen des Carolo Cups ausgewählt. Für den Einparkvorgang werden zwei Infrarotsensoren (nachfolgend: IR) vom Typ Sharp GP2D120, der Gierratensensor vom Typ LPR510AL und Hallsensoren zur Geschwindigkeitsermittlung verwendet.

Infrarotsensoren:

Die Positionen der IR sind im Artikel Sharp GP2D120 definiert und beschrieben. Der erste IR ist seitlich vorne am Fahrzeug montiert und wird dafür verwendet, die Parklücke zu finden und den Abstand zum seitlich parkenden Hindernis zu messen. Der zweite IR ist hinten-rechts angebrachte und misst den Abstand zum hinteren Hindernis, sobald sich das Fahrzeug zwischen den beiden Hindernissen befindet. Anhand des Abstandes wird entschieden, ob das Fahrzeug noch ein Stück vorfahren muss oder nicht, um dem hinteren Fahrzeug Platz zum Ausparken zu lassen.

Gierratensensor:

Um die Winkellage des Fahrzeugs vermessen zu können, wird ein Gierratensensor verwendet. Die Änderung von Rechts- auf Linkseinschlag während des Einparkens wird durch eine vorher berechnete Winkellage β (siehe Berechnung nötiger Größen) gesteuert. Außerdem wird der Sensor dafür eingesetzt, das Anhalten des Fahrzeugs zu erreichen, sobald der Winkel des Gyroskops 0 rad (0°) erreicht.

Hallsensor (Geschwindigkeitsmessung):

Die Geschwindigkeit wird über Hallsensoren ermittelt. Über die Ableitung der Geschwindigkeit wird die Streckenmessung durchgeführt. Diese dient dem Zweck, die Parklücke zu vermessen und bestimmte Kurzstrecken, wie z.B. das Weiterfahren nach Lückenfindung, definiert zurückzulegen.

Autor: Sascha Dienwiebel (Diskussion) 18:23, 3. Feb. 2014 (CET)

Autor: Martin Berysztak (Diskussion) & Adem Hadziric (Diskussion) 14:39, 22. Jan. 2015 (CET)

Der Einparkalgorithmus

Einbindung des Einparkalgorithmus in die Simulink Umgebung

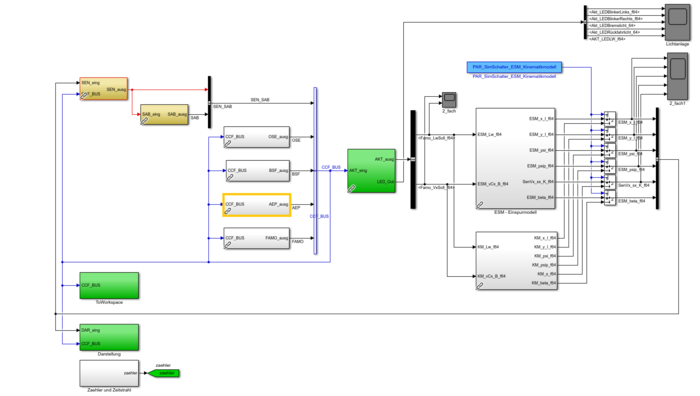
Das Hauptmodell für die Offline Simulation ist in der folgenden Abbildung dargestellt. Das Einparken wurde im Block AEP - Autonomes Einparken implementiert (orange hinterlegt dargestellt) und besitzt in der Online-Umgebung auf der Dspace Box denselben Aufbau, mit dem Unterschied, dass dort die Sensorwerte und Fahrbahn nicht simuliert werden müssen. Der gesamte Bus steht der Software zur Verfügung. Der Aufbau des Blocks und dessen internen Funktionen zur Umsetzung des Einparkalgorithmus findet sich in diesem Link wieder.

Autor: Sascha Dienwiebel (Diskussion) 18:24, 3. Feb. 2014 (CET)

Auswahl des Einparkmodus

Um das Einparkmanöver zu starten, muss zu Beginn das Simulink-Modell start.m Datei in MATLAB geöffnet werden. Für den Einparkmodus bestehen die Möglichkeiten, nach der Lückenfindung direkt einzuparken (Simulinkmodus = 3) oder stehen zu bleiben (Simulinkmodus = 2). Beim Online-Model muss beachtet werden, dass vor der Betätigung des AEP-Tasters, die Aktuatoren ausgeschaltet werden, damit die Kalibrierung des Gierratensensors gemacht wird. Hierzu muss der Hebel, der sich hinten am Fahrzeug befindet, in die Mittelstellung gebracht werden.

Alle weiteren Einstellungen sind optional und werden in diesem Link erläutert.

Autor: Sascha Dienwiebel (Diskussion) 18:24, 3. Feb. 2014 (CET)

Autor: Martin Berysztak (Diskussion) & Adem Hadziric (Diskussion) 14:39, 22. Jan. 2015 (CET)

Auswahl der geeigneten Geschwindigkeit

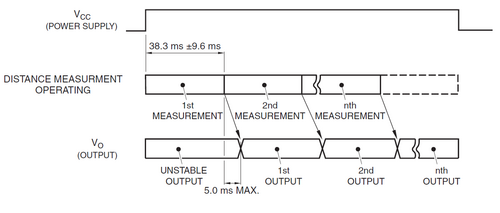
Der vorangegangenen Abbildung aus dem Datenblatt "Sharp-GP2D120.pdf" (siehe Infrarot Sensor) ist zu entnehmen, dass maximal eine Zeit für eine Messung benötigt wird, von:

$t= 38,3\,ms + 9,6\,ms + 5\,ms = 52,9\,ms$.

Sicherheitshalber wird davon ausgegangen, dass sich in der größten Lücke ein weiteres Hindernis mit den Maßen 10cm x 10cm befindet. Um diese erkennen zu können, sollten mindestens drei Messungen im Bereich des Hindernisses stattfinden. Die benötigte Zeit für diese drei Messungen beträgt demnach:

$t=3\cdot 52,9\,ms = 158,7\,ms.$

Da sich die Geschwindigkeit aus dem Weg (s) geteilt durch die Zeit (t) berechnet und der Weg in diesem Fall der Länge des Hindernisses entspricht, resultiert daraus eine maximale Geschwindigkeit von:

$v= \frac{0,1\,m}{158,7\cdot10^{-3}\,s} =0,63\,\frac{m}{s}.$

Zu beachten ist jedoch, dass aktuell (Stand WS 14/15) die Geschwindigkeit für das Einparkmanöver +/- 0,8m/s beträgt. Aufgrund der Haftreibung war zur Zeit der Tests eine niedrigere Geschwindigkeit nicht möglich.

Autor: Sascha Dienwiebel (Diskussion) 18:24, 3. Feb. 2014 (CET)

Autor: Martin Berysztak (Diskussion) & Adem Hadziric (Diskussion) 15:17, 22. Jan. 2015 (CET)

Berechnung nötiger Größen

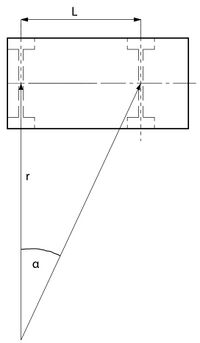
Das Fahrzeug besitzt einen maximalen Lenkeinschlag in eine Richtung von alpha = 23°. Kombiniert mit dem Radstand L = 0,265m ergibt dies einen Wendekreisradius um die Mitte der Hinterachse von:

$r= \frac{L}{tan(\alpha)} = \frac{0,265\,m}{tan(25^\circ)} = 0,5683\,m.$

Die folgende Abbildung zeigt eine Skizze zur Herleitung der Wendekreisradiusberechnung.

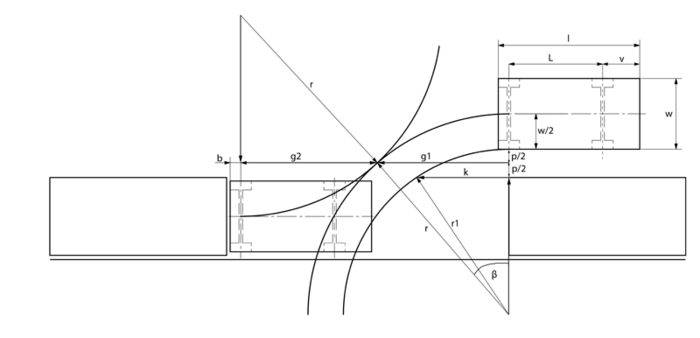
Für die Berechnung der notwendigen Parklücke spielt der Wendekreisradius (r), die Breite des Fahrzeuges (w), die Länge des Fahrzeugs von der Mitte der hiteren Achse bis zum Heck (b) und der seitliche Abstand zum Hindernis (p) eine wichtige Rolle. Die nachfolgende Abbildung zeigt eine Skizze des Fahrzeugs und dessen Einparkmanövers.

Notwendige Größen für den Vorgang des Einparkens sind:

Die allgemeinen Maße des Fahrzeugs

Breite w = 0,290m

Radstand L = 0,265m

Abstand Mitte Vorderachse nach Vorne v = 0,065m

Abstand Mitte Hinterachse zum Heck b = 0,100m

Wendekreisradius r = 1,1318m

Der seitliche Abstand zum Hindernis p = variabel

Wird der Einparkvorgang gestartet, sobald die Mitte der Hinterachse des Fahrzeugs auf Höhe der Heckkante des vorderen Hindernisses liegt, müsste die Parklücke, wie der vorangegangenen Abbildung zu entnehmen ist, die Summe aus b, g1 und g2 sein. Die Abstände g1 und g2 sind dabei gleich groß und berechnen sich nach dem Satz des Pythagoras wie folgt:

$g1 = \sqrt[]{r^2-(r-\frac{w}{2}-\frac{p}{2})^2}$

Dies würde zu einer größeren Lücke führen, als eigentlich nötig, da die Möglichkeit besteht, nach Findung des vorderen Hindernisses eine weitere Strecke k nach vorne zu fahren. Dadurch wird gewährleistet, dass kein Platz verschenkt und während des Einparkvorgangs so nah wie möglich am Hindernis vorbeigefahren wird. Demnach wird für die Größe der nötigen Parklücke (g) folgende Formel verwendet:

$g = 2\cdot \sqrt[]{r^2-(r-\frac{w}{2}-\frac{p}{2})^2}+b-\sqrt[]{(r-\frac{w}{2})^2-(r-\frac{w}{2}-p)^2}$

Anhand dieser Formel wird deutlich, dass sich die nötige Parklücke danach richtet, wie groß der Abstand zum Hindernis ist. In der Regel ist der Abstand p nicht gleich 0. Dies würde bedeuten, dass das einparkende Fahrzeug bereits sich direkt am stehenden Fahrzeug befindet. Der Punkt, dass das Fahrzeug mittig der Straße fahren soll und die Tatsache, dass der Infrarotsensor erst ab einem Abstand von 4cm zuverlässige Werte zurückgibt (siehe GP2D120), setzt einen angenommenen Mindestabstand zur Berechnung voraus. In diesem Fall wird ein Abstand p = 15cm vorausgesetzt. Diese Annahme führt zu einer Mindestgröße der Parklücke von g = 1m. Durch geringe Vergrößerung des Abstandes p, Kürzung des Fahrzeugs oder Erhöhung des Einschlagwinkels würde auch eine kleinere Parklücke ausreichen. Der seitliche Abstand zum Hindernis darf allerdings nicht größer als die Hälfte des Wendekreisradius sein. Bei diesem Fall werden sämtliche oben genannten Berechnungen außer Kraft gesetzt.

Die Berechnung des Umschlagwinkels $\beta$ ist ebenfalls vom Abstand p abhängig und wird erst berechnet, wenn die Lücke gefunden und das Fahrzeug neben dem vorderen Hindernis steht.

$\beta = \arccos(\frac{r-\frac{w}{2}-\frac{p}{2}}{r})$

Ebenso wird an dieser Stelle der Weg berechnet, den das Fahrzeug noch vorwärts fahren soll, um den vorhandenen Platz so effizient wie möglich zu nutzen. Je näher beim Einparken an dem vorderen Hindernis vorbeigefahren wird, desto weniger Platz wird während des gesamten Einparkvorgangs benötigt. Da sich beim Finden des vorderen Hindernisses die Vorderachse des RC Fahrzeuges auf höhe dessen Hecks befindet und der Einparkvorgang so kalkuliert wird, dass sich erst mal die Mitte der Hinterachse des RC Fahrzeuges auf Höhe des Hecks des vorderen Fahrzeugs befindet, muss auf jeden Fall die Strecke der Summe aus Radstand (L) und Mitte der Hinterachse zur Front (v) gefahren werden. Auf diesen Wert wird dann noch der Parameter k addiert, welcher sich wie folgt berechnet und bereits Teil der Parklückenberechnung ist:

$k = \sqrt[]{(r-\frac{w}{2})^2-(r-\frac{w}{2}-p)^2}$

Da bei allen Parkmanövern (offline- und online-Modus), das Fahrzeug eine zu weite Strecke nach vorne gefahren ist, ist die benötigte Länge der Vorausfahrt reduziert worden. Hier ist über Tests rausgekommen, dass der Abzug der Größe k weggelassen werden kann.

Autor: Sascha Dienwiebel (Diskussion) 18:24, 3. Feb. 2014 (CET)

Autor: Martin Berysztak (Diskussion) & Adem Hadziric (Diskussion) 14:39, 22. Jan. 2015 (CET)

Ausblick

Aktuell ist der Einparkmanöver am Fahrzeug möglich. Im nächsten Schritt könnte nun die Verknüpfung zwischen der Reglung für die Geradeausfahrt, mit der Geradeausfahrt für das Einparkmanöver gemacht werden. Aktuell wird die Geradeausfahrt beim Einparken über die Vorgabe eines 0 rad (0°) Lenkwinkels durchgeführt.

Zusätzlich ist die Lösung für die Berechnung des Umschlag Lenkwinkels über einen zusätzlichen Parameter realisiert worden. Hier muss folgend geprüft werden, warum genau dieser Wert ohne die Reduzierung zu groß war.

Aktuell ist keine Funktion für die Verhinderung von Zusammenstößen mit Hindernissen vorhanden. Hierzu könnte der erste Ansatz eines Konzeptes verwendet werden, welches hier | Kollisionskontrolle abgelegt ist.

Aktuell sthet das Fahrzeug nach dem Parkmanöver, relativ Parallel zu Fahrbahn (< 5°). Da das Fahrzeug vorher dauerhaft einen schrägen Schlusslenkwinkel hatte, wurde dem geforderten Endwinkel (siehe Einpark Parameter) der Wert von 9 Grad zugeteilt. Dieser Wert ist anhand von mehrfachen Tests als optimal ermittel worden.

Autor: Martin Berysztak (Diskussion) & Adem Hadziric (Diskussion) 16:39, 22. Jan. 2015 (CET)

Projektergebnisse SS14

Hier ist ein auskommentierter Teil der nicht mehr dem Standart enspricht. Alle dort vermerkten Änderungen wurden in die bestehenden Artikel eingefügt.

Quellen / Weiterführende Literatur

Powerpoint Datei mit allen Bildern zum Ändern der Bilder in diesem Artikel[1]