BSF - Bahn- und Spurführung

→ zurück zum Hauptartikel: Praktikum SDE

Einleitung und Ziel

Im Rahmen des SDE-Praktikums beinhaltet ein Arbeitsbereich die Bahnplanung und die Spurführung. Die Tätigkeit unterteilt sich in die Bereiche Bahnplanung und Autonome Längs- und Querregelung. Im Sommersemester 2016 und im Wintersemester 2016/2017 wurde der Themenbereich von Marcus Irmer und Robin Kirsch bearbeitet. Die Dokumentation beruht auf der Vorarbeit von Daniel Block und Torben Petersen. Im Sommersemester 2018 wurde darauf aufbauend die Thematik von Benedikt Wulowitsch und Leonard Herbstmann bearbeitet. In den Anforderungen und auch dem Pflichtenheft für das SoSe 2018 wurde als Aufgabe die Optimierung der Regler vorgesehen. Diese sind bisher jedoch nur in der Simulationsumgebung validiert worden.

Das Thema Autonome Längs- und Querregelung beinhaltet folgende Aufgaben:

• Analyse Istgeschwindigkeitssignal
• Analyse Gierrate
• Regelung längs
• Regelung quer

Zur Querregelung ist neben der eigentlichen Reglerauslegung das Querführungskonzept und die Parametrisierung des Einspurmodells (ESM) erforderlich.
Das Ziel der Aufgabe ist die Auslegung der Längs- und Querregelung des Fahrzeugs.

Analyse Istgeschwindigkeit

Bei der Istgeschwindigkeit wurde auf den Ergebnissen der vorangegangenen Semester zurückgegriffen. Siehe Dazu: Analyse Istgeschwindigkeit

Analyse Gierrate

Bei der Istgeschwindigkeit wurde auf den Ergebnissen der vorangegangenen Semester zurückgegriffen. Siehe Dazu: Analyse Gierrate

Längsregelung

Die Längsregelung des Fahrzeugs erfordert eine exakte Bestimmung der Sollgeschwindigkeit. Aus diesem Grund wird in den folgenden zwei Abschnitten das Konzept zur Bestimmung der Sollgeschwindigkeit betrachtet. Die Längsregelung soll im Groben so funktionieren, dass in Kurven die Längsgeschwindigkeit reduziert wird.

Konzept zur Bestimmung der Sollgeschwindigkeit

SenKam - Kamera (offline)

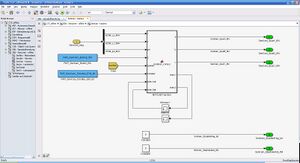
<br\>Die Sollgeschwindigkeit des Fahrzeugs wird aus dem Krümmungsradius der Fahrbahn bestimmt, um die Geschwindigkeit in Abhängigkeit der Kurve anzupassen. Die im Online-Modus von der Kamera erfasste Fahrbahn wird mit einer Parabel im Fahrzeug-Koordinatensystem modelliert. Diese ist bestimmt über die drei Koeffizienten a, b und c. Nach der allgemeinen Parabelgleichung ax²+bx+c beschreibt a die Krümmung der Kurve und wird im Block SenKam - Kamera in den Kameraparameter a geschrieben und als Signal SenKam_SpurA_f64 ausgegeben.<br\>

Im Offline-Modus wird der Kameraparameter a aus der Position und der Richtung des im Einspurmodell simulierten Fahrzeugs berechnet. Die Parameter ESM_x_I_f64 und ESM_y_I_f64 beschreiben die Position des Fahrzeugs. Die Richtung des Fahrzeugs steht im Parameter ESM_psi_f64. Der SenKam - Kamera-Block des Offline-Modells wird in der Abbildung SenKam - Kamera (offline) dargestellt.

Die Sollgeschwindigkeit wird im Online-Modell und im Offline-Modell im rechts dargestellten Block BSFVx - Bestimmung Sollgeschwindigkeit unter BSF - Bahnplanung und Spurfuehrung bestimmt. Die Eingänge des Blocks sind die Kameraparameter SenKam_SpurA_f64 und SenKam_SpurB_f64, die Vorausschauweite BsfQuer_Vorausschauweite_f64 und eine maximal zulässige Querbeschleunigung PAR_BsfQuer_a_max. Innerhalb des Subsystems Berechnung V_Soll wird zum einen der Kurvenradius der Bahnkurve in Abhängigkeit der Vorausschauweite berechnet. In Kombinatino mit der Querbeschleunigung und dem aktuellen Kurvenradius wird eine Sollgeschwindigkeit ermittelt, welche am Ausgang des Bausteins abgerufen werden kann.<br\>

Implementierung V_Soll

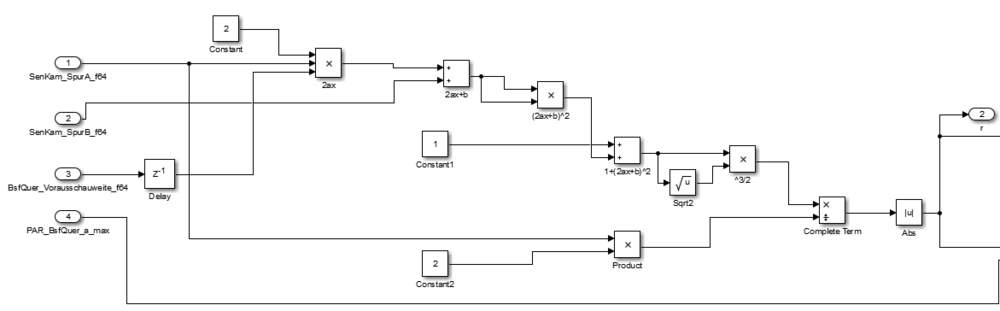
Die nebenstehende Abbildung zeigt die Programmierung zur Berechnung des Kurvenradius innerhalb des Subsystems. Die Berechnung liegt folgender Formel zur Berechnung eines Krümmungskreises zur Grunde:

$f(x) = \frac{(1+f'x^2)^{3/2}}{f''(x)}$

Das Kurvenpolynom hat den Grad 2 und lässt sich somit schreiben als:

$f(x) = ax^2+bx+c$

Durch das zweimalige differenzieren dieses Polynoms ergeben sich folgende Polynome:

$f'(x) = 2ax+b$
$f''(x) = 2a$

Wenn die beiden Ableitungen nun in die vorangegangene Formel zur Berechnung des Krümmungskreises eingesetzt werden, ergibt sich folgende Formel:

$f(x) = \frac{(1+(2ax+b)^2)^{3/2}}{2a}$

Exakt diese Formel ist in der nebenstehenden Simulink-Programmierung abgebildet. Für Es wurde von der Berechnung der Absolutwert gebildet und an den Ausgangsparameter r weitergeleitet.

Berechnung Kurvenradius

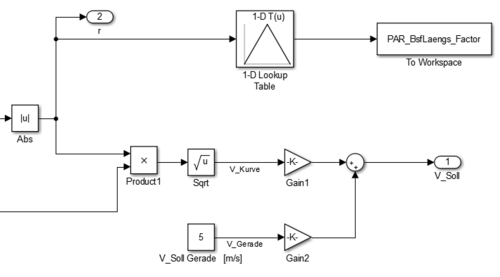
Damit aus dem bestimmten Kurvenradius der Fahrbahn eine Sollgeschwindigkeit ermittelt werden kann, wird sich folgender Formel bedient: $V_{Soll} = \sqrt{a_{max} \cdot r}$ diese Formel bezieht die maximale Querbeschleunigung mit ein ist in der Abbildung "Berechnung Sollgeschwindigkeit" in Simulink programmiert.

Der Lookup-Table, an welchen eine Konstante angeschlossen ist, dient dazu, den Sollwert für die Geschwindigkeit zwischen V_Kurve und V_Gerade umzuschalten. Die Konstante kann Werte zwischen Null und Eins annehmen. Die Geschwindigkeit V_Kurve wird mit diesem Faktor verstärkt und die Geschwindigkeit V_Gerade wird mit dem 1-Faktor verstärkt. Sollte sich das Fahrzeug also in einer Kurve befinden, so ist der Wert der Konstante bei 1 und die errechnete Sollgeschwindigkeit für die Kurvenfahrt wird an den Ausgang V_Soll weitergeleitet. Wird hingegen keine Kurve gefahren, so ist die Konstante Null und der feste Wert der Sollgeschwindigkeit für eine Geradeausfahrt wird an den Ausgang übermittelt. Diese Programmierung verhindert das Springen der Sollgeschwindigkeit, sobald aus der Geraden in eine Kurve gelenkt wird, oder andersherum.

Berechnung Sollgeschwindigkeit

Reglerentwurf

Zum besseren Verständnis wurde zusätzlich ein allgemeiner Regelkreis für die Längsführung des Fahrzeuges aufgestellt.

allgemeiner Regelkreis Längsregler

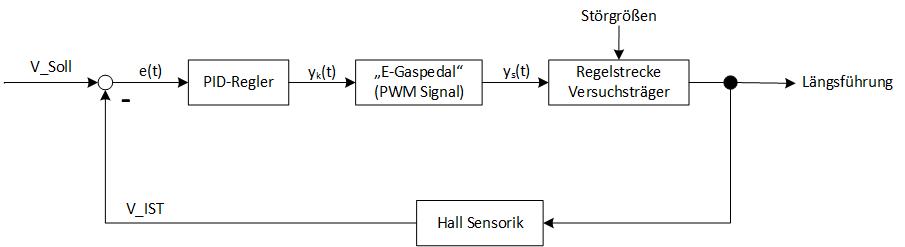
Die Parameter V_Soll und V_IST sind die gewünschte Sollgeschwindigkeit und die tatsächliche Geschwindigkeit des Fahrzeuges. Die Geschwindigkeit wird über ein PWM Signal gesteuert. Erfasst wird sie über eine Hall Sensorik. In den Regelkreis eingehende Störgrößen beschreiben Problematiken wie Schlupf und verschiedene Haftreibungen der Räder oder Probleme bei der Übersetzung.
Eine detailierte Beschreibung des Regelkreises wird folgend anhand des Simulink-Modells verdeutlicht.

Für den Längsregler wurde ein separates Simulink-Modell angelegt, damit der Regler besser veranschaulicht werden kann. Der Regler besitzt einen P-, I- und D-Anteil.

Testumgebung Längsregler (Originaldatei)

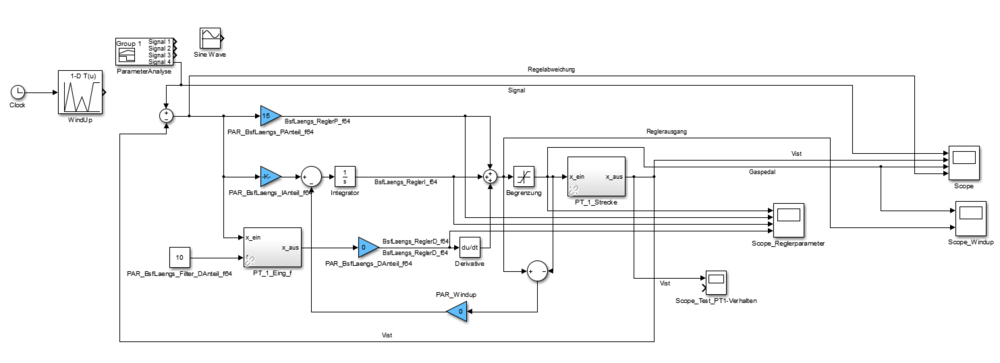
Für die Untersuchung der Regler-Parameter wurde ein Einheitssprung verwendet. Es wurden dabei folgende Feststellungen gemacht.

• Der P-Anteil ist für die Größe des "Einheitssprungs" verantwortlich. Mit größerem P-Anteil stellt sich außerdem ein zunehmendes Überschwingen ein.
• Mit dem I-Anteil werden die Stellgröße und der P-Anteil geglättet, jedoch ist für eine glatte Stellgröße ein sehr hoher I-Anteil erforderlich (größer als 150).
• Durch den D-Anteil kann der negative Ausschlag zu Beginn verringert werden. Mit größerem D-Anteil nimmt die Schwingung der Stellgröße zu.

Die Auswirkungen der Parameter wurden in einer Testreihe untersucht. Die Plots sind im Ordner trunk/Teams/BSF/Bilder Doku/Reglerentwurf zu finden.
Wenn nur ein D-Anteil vorhanden ist, ist die Stellgröße nicht konstant. Im Test wurden für den D-Anteil die Werte [5 15 50] verwendet und der Wert 15 gewählt, weil die Totzeit am geringsten ist. Für größere Werte nimmt sie nicht weiter ab. Im Test des I-Anteils wurde mit verschiedenen Werten experimentiert, eine konstante Stellgröße wurde erst ab einem Wert von 170 erreicht. Bei kleineren Werten konnte im Plot der Stellgröße noch eine Schwingung wahrgenommen werden. Sobald der D-Anteil hinzukommt, geht die konstante Stellgröße verloren, jedoch wird der negative Ausschlag verringert. Allerdings kann auch mit einem sehr hohen I-Anteil von 500 die Stellgröße nicht geglättet werden.

Siehe Dazu: Auslegung der Reglerparameter

Längsregelung Wintersemester 2018/19

Im Wintersemester 2018/19 wurde die Längsregelung von einer Steuerung in eine eigentliche Regelung überführt. Vorher wurde die Sollgeschwindigkeit mit einer Verstärkung von "1" verstärkt, und als Ist-Wert ausgegeben, sodass nie eine Regelabweichung existierte. Nun wurde eine Kopplung zwischen dem Ausgang des Reglers und der Ist-Geschwindigkeit geschlossen. Für die Kopplung wurde aus dem Bus das Signal "BsfLaengs_Gaspedal_f64" genommen. Dies ist das Signal, welches vom Ausgang des Längsreglers beeinflusst wird. Dieses Signal hat einen Wertebereich von -1 bis +1. So wurde innerhalb des Lookup-Tables unter "Table data" der Vektor [-1 0 1] angelegt. Als erste Annahme für die Simulation wurde eine Maximalgeschwindigkeit von 0.75 m/s in beide Fahrtrichtungen angenommen. Unterhalb des Punktes "Breakpoints1" im Lookup-Table wurde folgender Vektor eingefügt: [-0.75 0 0.75] Die nachfolgende Abbildung zeigt den besagten Lookup-Table

Kopplung PWM-Signal mit der Ist-Geschwindigkeit

Damit die Regelung nun vollständig ist, wurden die Parameter des Längsreglers angepasst. Die Findung der Parameter fand empirisch statt, sodass nun folgende Parameter gültig sind:

PAR_BsfLaengs_PAnteil_f64                   = 5;
PAR_BsfLaengs_IAnteil_f64                   = 2;
PAR_BsfLaengs_DAnteil_f64                   = 0;

PAR_BsfLaengs_Filter_DAnteil_f64            = 10;  % Eckfrequenz des PT1-Filters für den gefilterten D-Anteil

Zum Test des Regelkreises wurde in der nachfolgenden Abbildung eine Sollgeschwindigkeit von 0.6 m/s nach einer Simulationszeit von 10s eingeleitet. Der rote Verlauf stellt den Sprung dar, der grüne Verlauf stellt die Sollgeschwindigkeit dar und der blaue Verlauf soll die Regelabweichung darstellen.

Sprung auf den Längsregler

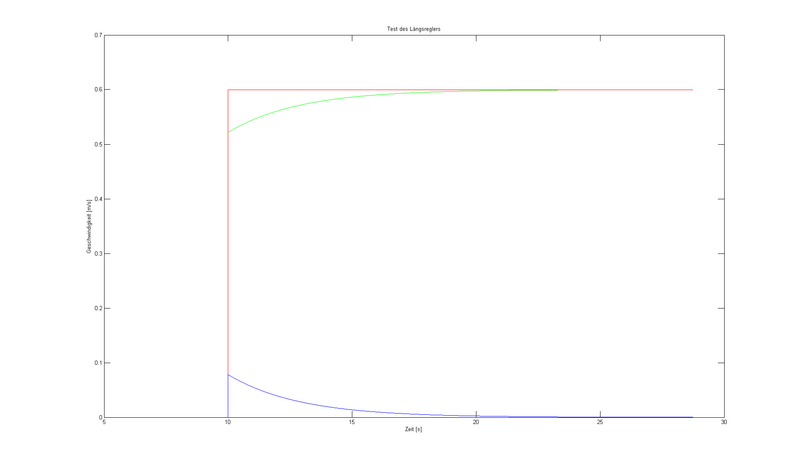
Querregelung

Für die Querregelung wird verglichen, welche Bahn das Auto fahren würde (Istgröße) und welche Bahn das Auto fahren soll (Sollgröße). Zuerst wird die Bestimmung der Sollgröße beschrieben.

Querführungskonzept

Die Querführung des Fahrzeuges wird in zwei Bereiche unterteilt. Der erste Aspekt beinhaltet die Bahnplanung, die im Folgenden in ihrer theoretischen Grundlage und der Umsetzung in Simulink dargestellt wird. Die Querregelung wird im Anschluss beschrieben.

Layout BSF_Regelung (Originaldatei)

Als Grundlage für das Querführungskonzept dient die Sollbahn, die durch das Team OSE - Objekt- und Spurerkennung aufgrund der Analyse der zu fahrenden Strecke mit Hilfe eines Polynoms zweiten Gerades, das durch die Parameter a, b und c eindeutig beschrieben ist, zur Verfügung gestellt wird. (Wichtig: trunk/Anforderungsmanagement/Lastenheft/Schnittstellendokumentation.docx beachten)
Da in dieser Anwendung aufgrund der Geometrie des Fahrzeugs ein Vergleich der Soll- und Ist-Bahn nicht sinnvoll ist, muss ein Punkt auf der Bahn in der Vorausschauweite x prädiziert werden, an dem sich das Fahrzeug bei idealem Lenkwinkel und der aktuellen Geschwindigkeit befinden würde. Der ideale Lenkwinkel kann aber nicht bestimmt werden. Aus diesem Grund muss eine Abschätzung der Querabweichung von der einfachen Geradeausfahrt getroffen werden. Dabei wird der derzeitige Lenkwinkel als Referenz verwendet. Die Regeldifferenz des Querreglers bildet sich somit aus dem Punkt auf der Sollbahn und der prädizierten Positionsabschätzung.

Vorausschauweite

Die Vorausschauweite x wird abhängig von der aktuellen Geschwindigkeit des Fahrzeugs berechnet. Dazu wird eine LUT verwendet, ihre Parameter sind in der Parameterdatei param_BSF.m hinterlegt. Es sind die Werte PAR_BSFQuer_LookupVorausschauweite_Vx_f64 mit aktuell [0 0.2 0.30 0.8 3] und PAR_BSFQuer_LookupVorausschauweite_X_f64 mit aktuell [0.4 0.4 0.8 0.8 1.5]. Wichtig: Die Kamera mit der nachgeschalteten Bildverarbeitung liefert nämlich nur Ergebnisse für dem Bereich zwischen 0,4 m und 1,5 m vor dem Fahrzeug. Am besten arbeitet das Fahrzeug bei derzeitiger Konfiguration mit 0,8. Aus diesem Grund wurde mit der LUT der Wert auf diesen Bereich begrenzt, die Werte unter bzw. über 0,8 werden nur bei sehr geringer bzw. sehr hoher Geschwindigkeit angenommen. Es besteht aber noch die Möglichkeit auf einen manuellen Wert umzustellen, dies kann in ControlDesk® auf dem Layout BSF_Regelung gemacht werden, vgl. Abbildung Layout BSF_Regelung.

Sollbahnbestimmung

Im Folgenden soll die Bestimmung des Punktes auf der Sollbahn beschrieben werden. Die Bahn wird als ein Polynom zweiten Gerades, einer Parabel, approximiert. Die allgemeine Formel lautet:
$f(x) = a \cdot x^2 + bx + c \qquad(1)$

Die Abbildung Schema der Sollbahn zeigt die Sollkurve im Fahrzeug-Koordinatensystem. Auch die Lage des Sollpunktes auf der Kurve ist dort qualitativ zu sehen.

Schema der Sollbahn
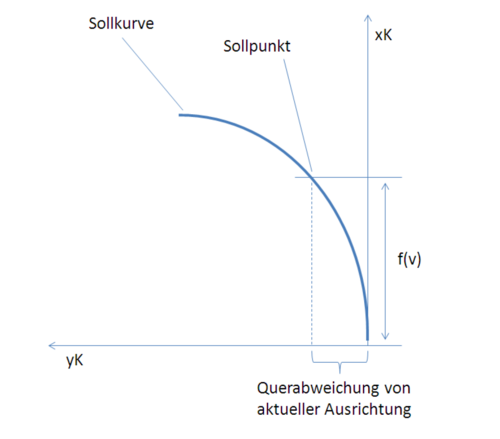
Quelle: trunk/Dokumentation/Dokumentation_LaTex/Carolo_Doku_2012.pdf

Die Bestimmung des prädizierten Punktes des Fahrzeuges auf der Ist-Bahn geschieht unter folgender Annahme: Ist der Lenkwinkel des Fahrzeuges gleich Null, existiert zwischen prädiziertem Ist-Punkt und der aktuellen Ausrichtung des Fahrzeuges keine Querabweichung. Fährt das Fahrzeug nicht exakt geradeaus, befindet es sich auf einer Kreisbahn, die bei stationär statischem Lenkwinkel konstant ist.
Der Radius dieser Kreisbahn lässt sich aus der stationären Gierrate und der Geschwindigkeit wie folgt bestimmen:
$r=\frac{v_0}{\dot\psi} \qquad(2)$
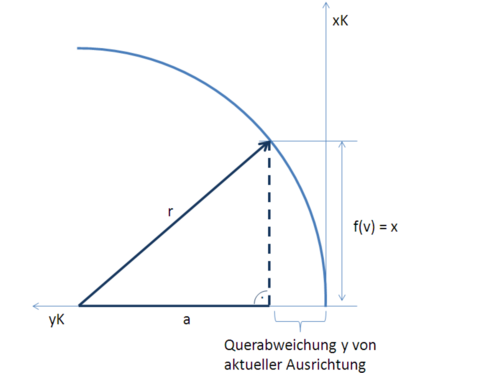
Die Abbildung Schema der Istbahn zeigt die prädizierte Istbahn im Fahrzeug-Koordinatensystem und den Zusammenhang zwischen Querabweichung y und Vorausschauweite x.

Schema der Istbahn
Quelle: trunk/Dokumentation/Dokumentation_LaTex/Carolo_Doku_2012.pdf

Zur Bestimmung der Querabweichung y wird der in der Skizze erkenntliche Zusammenhang zwischen dem Kreisradius r und der Vorausschauweite x verwendet. Dazu muss jedoch zuvor sichergestellt werden, dass die Vorausschauweite kleiner als der Betrag des erechneten Radius ist. Mit dem Satz des Phythagoras kann dann a wie folgt bestimmt werden:
$r^2=x^2+a^2\Leftrightarrow a^2=r^2-x^2\Leftrightarrow a=\sqrt{r^2-x^2}\qquad(3)$

Die Querabweichung y kann aus r und a bestimmt werden, sofern r positiv ist (Linkskurve):
$y=r-a \qquad(4)$

Falls r negativ ist (Rechtskurve), berechnet sich y wie folgt:
$y=r+a \qquad(5)$

Da die Vorausschauweite x unabhängig vom derzeitigen Kurvenradius r bestimmt wird, kann der Ausdruck unter der Wurzel in (3) negativ sein. Weil diese Berechnung unzulässig wäre, wird vorbeugend das Ergebnis der Vorausschauweitenberechnung mit einer Sättigungsfunktion begrenzt, die maximal 80 % des aktuellen Kurvenradius annimmt. Dieser Wert (80 % = 0.8) kann über den Parameter PAR_BSFQuer_VorausschauBegrenzung_f64 eingestellt werden.
Die Querabweichung der Sollbahn und die Querabweichung der Istbahn, jeweils bezogen auf die aktuelle Ausrichtung des Fahrzeuges, ergeben die Regeldifferenz für den Querregler. Aufgrund der Differenz zwischen Sollbahn und Istbahn bringt dieses Konzept eine bleibende Regelabweichung in der Kurve mit sich. Diese ist nur dann Null, wenn das Fahrzeug sich in der Geradeausfahrt befindet.

Siehe dazu: Querreglung Vorarbeiten

Reglerentwurf

Wie auch bei der Längsführung wurde für die Querregelung zur Übersicht ein allgemeiner Regelkreis aufgestellt.

allgemeiner Regelkreis Querregler

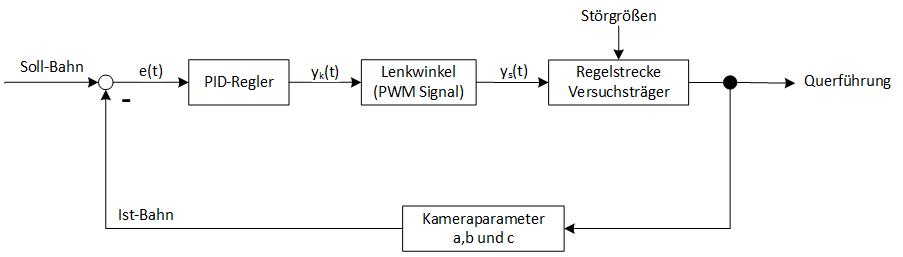
Die Parameter LW_Soll und LW_Ist beschreiben den gewünschten Lenkwinkel und den momentan erfassten Lenkwinkel. In den Regelkreis eingehende Störgrößen sind Probleme bei der Übertragung des Stellmotors für den Lenkwinkel. Eine detaillierte Beschreibung zu dem bisherigen Stand des aggierenden Reglers ist unter Querreglung Vorarbeiten zu finden.

Hier kommt noch ein Bild des Regelkreises aus Simulink rein!

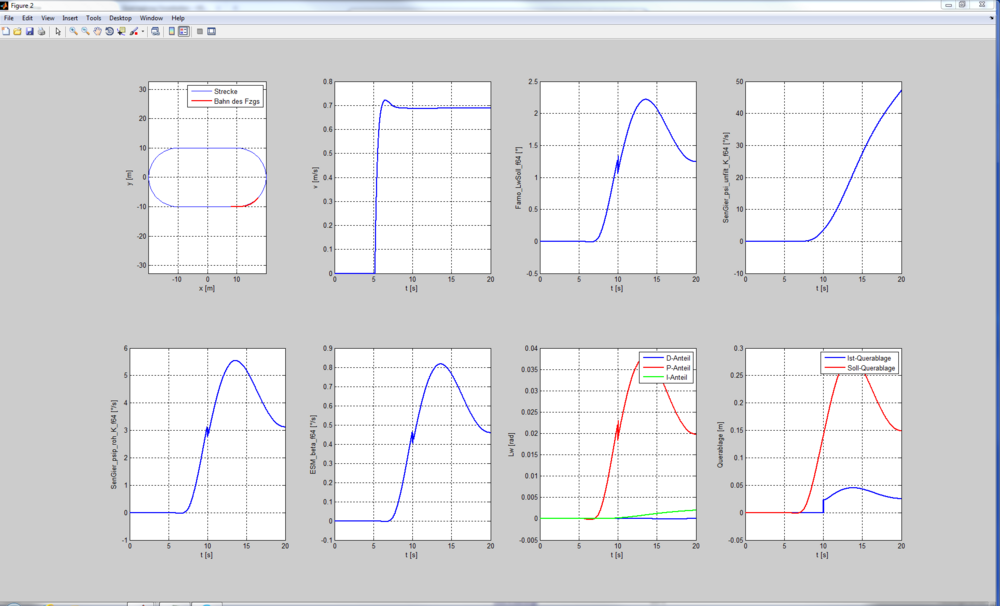
In der nachfolgenden Abbildung ist ein Plot dieser Querregelung dargestellt. Es wird oben links die aktuelle Fahrbahn in der Simulation angezeigt. Daneben befindet sich die aktuelle Geschwindigkeit, der Solllenkwinkel und die Gierrate Psi ungefiltert. In den vier Plots in der unteren Reihe befindet sich von links nach rechts der Gierwinkel Psi als Rohwert, allerdings gefiltert. Neben der gefilterten Gierrate ist die eigentliche Regelgröße, also der Lenkwinkel aus dem Einspurmodell in der Einheit Grad/Sekunde dargestellt. Neben diesem Plot befindet sich ein Plot der drei Reglerparameter. Zu Erkennen ist, dass der P-Anteil noch ein leichtes Schwingen hat, was für die Regelung aber nicht weiter kritisch ist. Als letzter Plot unten rechts befindet sich die Querablage des Fahrzeugs.

Plot der Querregelung

Ergebnis/ Zusammenfassung

Sommer 2018

• In der Simulation ist die richtige Funktion der Querregelung zu erkennen
• ein Einschwingen des Reglers ist in der Simulation kein Problem in Hinsicht auf das Einhalten der SOLL-Bahn
• Simulink Modelle sind optimiert - Einstellungen des P-,I- und D- Anteils sind ausschließlich in den Parametern vorzunehmen und nicht im Modell selbst
• Längsregelung ist zur Zeit noch inaktiv und ist stattdessen durch eine konstante Geschwindigkeit ersetzt
• Längsregelung ist jedoch in der Simulation funktionsfähig, so wird die Geschwindigkeit in Kurvenfahrten reduziert und auf geraden Strecken wieder erhöht
• Tests auf der Fahrbahn konnten mit dem aktuellen Stand im Sommersemester '18 noch nicht durchgeführt werden

Ausblick

Winter 2018/19

• Die Bestimmung der Ist-Geschwindigkeit könnte durch ein PT1 Glied, was das reale Verhalten des Autos wiederspiegelt modelliert werden. Dies würde eine noch höhere Modellgenauigkeit mit sich bringen.

Sommer 2017

• Feinjustierung der Parameter der Längsregelung am Fahrzeug
• Nach der Parametrisierung des Einspurmodells Querregler im Simulations-Modell auslegen
• Wenn Auslegung Querregler in Simulation erfolgreich, dann Feinjustierung am Fahrzeug
• Messung der Gierrate mit neuem Gierraten-Sensor
• Auslegung des ESM durch Justierung der Größen J, c_v und c_h
• Implementierung des Konzepts für Hindernisumfahrung in der Online-Simulation

Winter 2017

• Reglerparameter für Querregelung anpassen, sodass Regler schneller reagiert (enge Kurven, Hindernisse), dann Fahrgeschwindigkeit erhöhen
• Vorausschauweite lässt sich evtl. noch verbessern
• evtl. Sonderregelung für Querreglung bei erkannter Stopplinie: für eine feste Streckenlänge geradeaus fahren; dadurch lassen sich die Lücken auf der Kreuzung einfach kompensieren; Absprache mit Kamera-Team/Bildverarbeitung notwendig
• Implementierung des Konzepts zum Anhalten an Stopplinien
• in Hindernisumfahrung eigene Signalaufbereitung entfernen, Objektliste aus Signalaufbereitung verwenden, vgl. Vorarbeit
• Hindernisumfahrung in Simulation anpassen, dann auf AMR testen
• Kalman-Filter für Streckenverlauf, vgl. Vorarbeit; Absprache mit Kamera-Team/Bildverarbeitung notwendig

Sommer 2018

• Bisher konnten die Regler nur in der Simulation getestet werden, im kommenden Wintersemester wird ein Test auf der Fahrbahn erfolgen, sodass verfiziert werden kann, dass die in der Simulation gewählten Reglerparameter sich auch in der Praxis bewähren. Sollte sich heraussstellen das eine Nachoptimierung erforderlich ist, so wird dies auch im kommenden Wintersemester erfolgen.

• Das neu eingebaute Konzept zur Bestimmung der Sollgeschwindigkeit wird im kommenden Wintersemester auf der Fahrbahn erprobt. In der Simulation erwies sich die Berechnung anhand der Kameraparameter als sehr vielversprechend. Das Finetuning dieser Berechnung erfolgt ebenfalls im kommenden Wintersemester.

Einzelnachweise

Autor: Nils Brunnert
Überarbeitet: Daniel Block und Torben Petersen im Sommersemester 2014 und Wintersemester 2014/2015
Überarbeitet: Marcus Irmer und Robin Kirsch im Sommersemester 2016 und Wintersemester 2016/2017
Überarbeitet: Benedikt Wulowitsch und Leonard Herbstmann im Sommersemester 2018

---

→ zurück zum Hauptartikel: Praktikum SDE