Spurpolynom: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| Zeile 12: | Zeile 12: | ||
<math>\hat{y} = a \cdot \hat{x^{2}} + b \cdot \hat{x}+ c</math> | <math>\hat{y} = a \cdot \hat{x^{2}} + b \cdot \hat{x}+ c</math> | ||
unter der Bedingung gesucht, dass die Funktion | unter der Bedingung gesucht, dass die Funktion | ||
<math>V(a,b,c) = \sum_{i=1}^k (y_i-\hat{y_i})^2 = \sum_{i=1}^k(y_i-a \cdot x_i^2-b \cdot x_i - c)^2\qquad(1)</math> <br> | <math>V(a,b,c) = \sum_{i=1}^k (y_i-\hat{y_i})^2 = \sum_{i=1}^k(y_i-a \cdot x_i^2-b \cdot x_i - c)^2\qquad(1)</math> <br/> | ||
der Summe der Quadrate der Abstände der tatsächlichen y-Werte von berechneten <math>\hat{y}</math> -Werten ein Minimum hat. | der Summe der Quadrate der Abstände der tatsächlichen y-Werte von berechneten <math>\hat{y}</math> -Werten ein Minimum hat. | ||
Zur Bestimmung der Konstanten <math> a,b,c </math> in Gleichung (1) werden die partiellen Ableitungen <math>\frac{\partial V}{\partial a} </math>, <math>\frac{\partial V}{\partial b} </math> und <math>\frac{\partial V}{\partial c} </math> gleich null gesetzt, um jeweils das minimum zu erhalten:<br> | Zur Bestimmung der Konstanten <math> a,b,c </math> in Gleichung (1) werden die partiellen Ableitungen <math>\frac{\partial V}{\partial a} </math>, <math>\frac{\partial V}{\partial b} </math> und <math>\frac{\partial V}{\partial c} </math> gleich null gesetzt, um jeweils das minimum zu erhalten:<br> | ||
| Zeile 45: | Zeile 45: | ||
Dann könte man ein Vorhersagemodell für Fahrzeug erhalten. | Dann könte man ein Vorhersagemodell für Fahrzeug erhalten. | ||
[[Datei:Offline_KameraSignal.png|800px|thumb|links|Abb. 1 Offline Kamera modell]] | [[Datei:Offline_KameraSignal.png|800px|thumb|links|Abb. 1 Offline Kamera modell]] | ||
<br/> | |||
<br/> | |||
<br/> | |||
<br/> | |||
<br/> | |||
<br/> | |||
<br/> | |||
<br/> | |||
<br/> | |||
<br/> | |||
<br/> | |||
<br/> | |||
<br/> | |||
<br/> | |||
<br/> | |||
==Online Modell== | ==Online Modell== | ||
Version vom 27. April 2021, 23:36 Uhr
Autor: Junjie Lyu
Betreuer: Prof. Schneider
Einleitung
In diesem Artikel wird ein Spurpolynom des Carolo Cup Fahrzeugs beschrieben. Daher befasst sich dieser Artikel mit der Berechnung des Spurpolynoms.
Regressionsanalyse[1]
Anleitung
Ziel der Regressionsanalyse am häugigsten ist es, Beziehung zwischen einer abhängigen und einer oder mehreren unabhängigen Variable festzustellen, um ein Vorhersagemodell zu erstellen. Wenn nun zusätzliche Werte x ohne zugehörigen Wert y vorliegen, dann kann das angepasste Modell zur Vorhersage des Wertes von y verwendet werden.
Polynomische Regression
Im Falle der polynomischen Regression vom Grad 2 wird die Funktion unter der Bedingung gesucht, dass die Funktion
der Summe der Quadrate der Abstände der tatsächlichen y-Werte von berechneten -Werten ein Minimum hat.
Zur Bestimmung der Konstanten in Gleichung (1) werden die partiellen Ableitungen , und gleich null gesetzt, um jeweils das minimum zu erhalten:
Partielle Ableitung nach : dividiert durch ergibt:
Partielle Ableitung nach :
dividiert durch ergibt:
Partielle Ableitung nach :
dividiert durch ergibt:
Es entsteht wieder ein lineares Gleichungssystem in drei Variablen ,dessen Lösung die optimalen Konstanten liefert:
Offline Modell
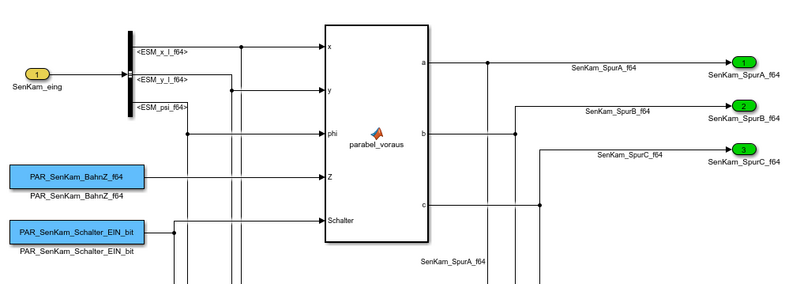
Eingabe-Variablen:
x und y: Koordinaten des Fahrzeugschwerpunktes in Weltkoordinaten phi: Fahrzeugrichtung in Weltkoordinaten. Z: die Bahnpunkte
Ausgabe-Variablen:
a,b,c: Koeffizienten einer Parabel, welche die Fahrbahn im Fahrzeug-Koordinatensystem bestmöglich nähert
Die Punkte werden bestimmt, die von (x,y) einen Abstand kleiner d haben. Die Punkte werden angenommen, die (x,y) immer maximal d/2 von der Laborbahn entfernt ist. Durch die angenommenen Punkte mit polynomischen Regression werden a,b,c beschrieben. Dann könte man ein Vorhersagemodell für Fahrzeug erhalten.
Online Modell
Literatur
→ zurück zum übergeordneten Artikel: Systemarchitektur des Fahrzeugs
→ zurück zum Hauptartikel: Praktikum SDE