Spurpolynom
Autor: Junjie Lyu
Betreuer: Prof. Schneider
Einleitung
In diesem Artikel wird ein Spurpolynom des Carolo Cup Fahrzeugs beschrieben. Daher befasst sich dieser Artikel mit der Berechnung des Spurpolynoms.
Regressionsanalyse[1]
Anleitung
Ziel der Regressionsanalyse am häugigsten ist es, Beziehung zwischen einer abhängigen und einer oder mehreren unabhängigen Variable festzustellen, um ein Vorhersagemodell zu erstellen. Wenn nun zusätzliche Werte x ohne zugehörigen Wert y vorliegen, dann kann das angepasste Modell zur Vorhersage des Wertes von y verwendet werden.
Polynomische Regression
Im Falle der polynomischen Regression vom Grad 2 wird die Funktion $ {\hat {y}}=a\cdot {\hat {x^{2}}}+b\cdot {\hat {x}}+c $ unter der Bedingung gesucht, dass die Funktion
$ V(a,b,c)=\sum _{i=1}^{k}(y_{i}-{\hat {y_{i}}})^{2}=\sum _{i=1}^{k}(y_{i}-a\cdot x_{i}^{2}-b\cdot x_{i}-c)^{2}\qquad (1) $
der Summe der Quadrate der Abstände der tatsächlichen y-Werte von berechneten $ {\hat {y}} $ -Werten ein Minimum hat.
Zur Bestimmung der Konstanten $ a,b,c $ in Gleichung (1) werden die partiellen Ableitungen $ {\frac {\partial V}{\partial a}} $, $ {\frac {\partial V}{\partial b}} $ und $ {\frac {\partial V}{\partial c}} $ gleich null gesetzt, um jeweils das minimum zu erhalten:
Partielle Ableitung nach $ a $: $ \longrightarrow {\frac {\partial V(a,b,c)}{\partial a}}=2\cdot \sum _{i=1}^{k}(y_{i}-a\cdot x_{i}^{2}-b\cdot x_{i}-c)\cdot (-x_{i}^{2}) $ dividiert durch $ k $ ergibt: $ \quad {\overline {y_{i}x_{i}^{2}}}=a\cdot {\overline {x_{i}^{4}}}+b\cdot {\overline {x_{i}^{3}}}+c\cdot {\overline {x_{i}^{2}}}\qquad (2) $
Partielle Ableitung nach $ b $:
$ \longrightarrow {\frac {\partial V(a,b,c)}{\partial b}}=2\cdot \sum _{i=1}^{k}(y_{i}-a\cdot x_{i}^{2}-b\cdot x_{i}-c)\cdot (-x_{i}) $ dividiert durch $ k $ ergibt: $ \quad {\overline {y_{i}x_{i}}}=a\cdot {\overline {x_{i}^{3}}}+b\cdot {\overline {x_{i}^{2}}}+c\cdot {\overline {x_{i}}}\qquad (3) $
Partielle Ableitung nach $ c $:
$ \longrightarrow {\frac {\partial V(a,b,c)}{\partial c}}=2\cdot \sum _{i=1}^{k}(y_{i}-a\cdot x_{i}^{2}-b\cdot x_{i}-c)\cdot (-1) $ dividiert durch $ k $ ergibt: $ \quad {\overline {y_{i}}}=a\cdot {\overline {x_{i}^{2}}}+b\cdot {\overline {x_{i}}}+c\qquad (4) $
Es entsteht wieder ein lineares Gleichungssystem in drei Variablen $ a,b,c $,dessen Lösung die optimalen Konstanten liefert:
$ a={{({\overline {y_{i}x_{i}^{2}}}-{\overline {y_{i}}}\cdot {\overline {x_{i}^{2}}})\cdot ({\overline {x_{i}^{2}}}-({\overline {x_{i}}})^{2})-({\overline {y_{i}x_{i}}}-{\overline {y_{i}}}\cdot {\overline {x_{i}}})\cdot ({\overline {x_{i}^{3}}}-{\overline {x_{i}}}\cdot {\overline {x_{i}^{2}}})} \over {({\overline {x_{i}^{4}}}-({\overline {x_{i}^{2}}})^{2})\cdot ({\overline {x_{i}^{2}}}-({\overline {x_{i}}})^{2})-({\overline {x_{i}^{3}}}-{\overline {x_{i}}}\cdot {\overline {x_{i}^{2}}})^{2}}} $ $ b={{{\overline {y_{i}x_{i}}}-{\overline {y_{i}}}\cdot {\overline {x_{i}}}-a\cdot ({\overline {x_{i}^{3}}}-{\overline {x_{i}}}\cdot {\overline {x_{i}^{2}}})} \over {{\overline {x_{i}^{2}}}-({\overline {x_{i}}})^{2}}} $ $ c={\overline {y_{i}}}-a\cdot {\overline {x_{i}^{2}}}-b\cdot {\overline {x_{i}}} $
Offline Modell
Eingabe-Variablen:
x und y: Koordinaten des Fahrzeugschwerpunktes in Weltkoordinaten phi: Fahrzeugrichtung in Weltkoordinaten. Z: die Bahnpunkte
Ausgabe-Variablen:
a,b,c: Koeffizienten einer Parabel, welche die Fahrbahn im Fahrzeug-Koordinatensystem bestmöglich nähert
Die Punkte werden bestimmt, die von (x,y) einen Abstand kleiner d haben. Die Punkte werden angenommen, die (x,y) immer maximal d/2 von der Laborbahn entfernt ist. Durch die angenommenen Punkte mit polynomischen Regression werden a,b,c beschrieben. Dann könte man ein Vorhersagemodell für Fahrzeug erhalten.
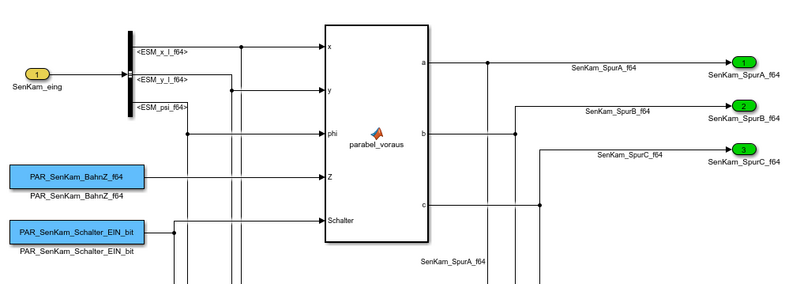
Online Modell
Eingabe Variablen werden durch Kamera erhilten
Ausgabe-Variablen:
a,b,c: Koeffizienten einer Parabel, welche die Fahrbahn im Fahrzeug-Koordinatensystem bestmöglich nähert
Literatur
Regressionsanalyse der Uni Leipzig
Bearbeiten von „Berechnung des Spurpolynoms“
→ zurück zum übergeordneten Artikel: Systemarchitektur des Fahrzeugs
→ zurück zum Hauptartikel: Praktikum SDE