Escape Game: Kugel-Balancierer: Unterschied zwischen den Versionen
Textbearbeitung und Referenzierung der Abbildungen |
|||
| Zeile 135: | Zeile 135: | ||
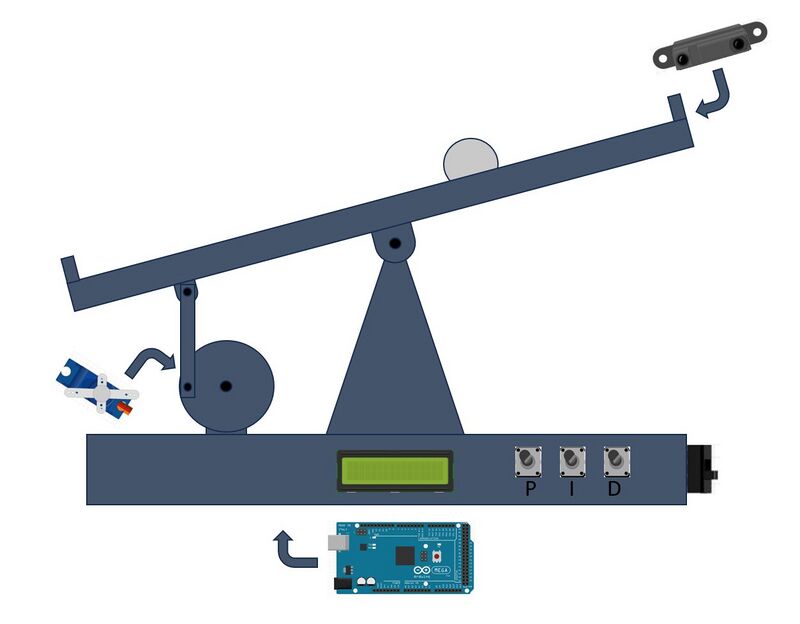
In der folgenden Abbildung 2 ist der funktionalen Systementwurf des Kugel-Balancierers dargestellt. Die mechanischen Elemente werden aus Holz bzw. mittels 3D-Druck erstellt. Mittels Servomotor kann der Drehwinkel einer Drehscheibe (Stellgröße) verändert werden, um die Laufbahn der zu balancierenden Kugel (in gelb dargestellt) zubewegen. An einer Seite der Laufbahn befindet sich ein Infrarot Distanzsensor, um die aktuelle Position dieser Kugel auf der Laufbahn zu erfassen, welche ebenfalls die Regelgröße des Systems darstellt. Diese soll durch einen auf dem Mikrocontroller (hier Arduino MEGA) ausgeführten PID Regler geregelt werden. Um das Escape Game zu starten und die P-, I- und D-Anteile des Reglers über die drei Rotary Encoder einzustellen, muss das System über den seitlichen Schalter eingeschaltet werden. Bei Erfolg wird ein Code über den Display ausgegeben. | In der folgenden Abbildung 2 ist der funktionalen Systementwurf des Kugel-Balancierers dargestellt. Die mechanischen Elemente werden aus Holz bzw. mittels 3D-Druck erstellt. Mittels Servomotor kann der Drehwinkel einer Drehscheibe (Stellgröße) verändert werden, um die Laufbahn der zu balancierenden Kugel (in gelb dargestellt) zubewegen. An einer Seite der Laufbahn befindet sich ein Infrarot Distanzsensor, um die aktuelle Position dieser Kugel auf der Laufbahn zu erfassen, welche ebenfalls die Regelgröße des Systems darstellt. Diese soll durch einen auf dem Mikrocontroller (hier Arduino MEGA) ausgeführten PID Regler geregelt werden. Um das Escape Game zu starten und die P-, I- und D-Anteile des Reglers über die drei Rotary Encoder einzustellen, muss das System über den seitlichen Schalter eingeschaltet werden. Bei Erfolg wird ein Code über den Display ausgegeben. | ||
[[Datei:FunktionalerSystementwurfBalancierer.jpg|mini|800px|left| | [[Datei:FunktionalerSystementwurfBalancierer.jpg|mini|800px|left|Abbildung 2: Funktionaler Systementwurf des Balancierers]] | ||
<br clear=all> | <br clear=all> | ||
| Zeile 143: | Zeile 143: | ||
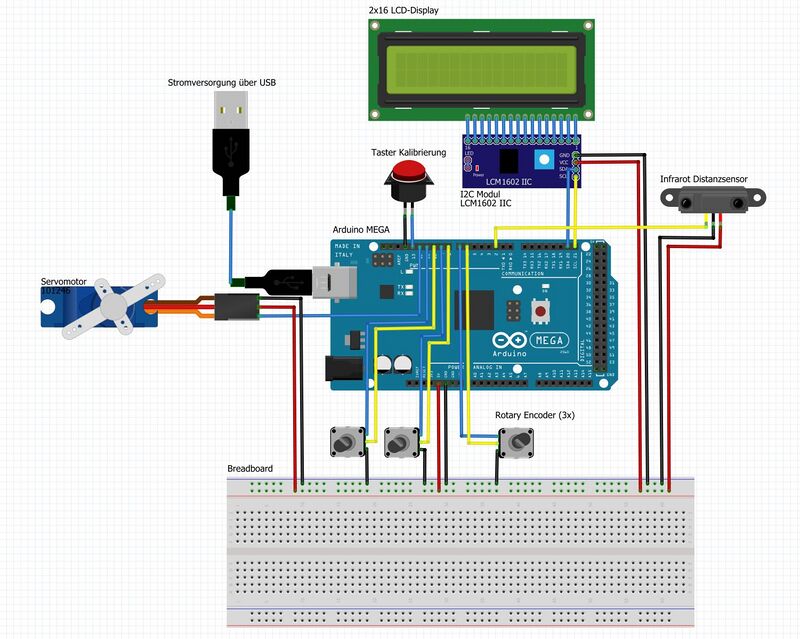
Als technischer Systementwurf für das Projekt wurde der folgende Verdrahtungsplan erstellt (siehe Abbildung 3). In diesem sind alle elektronischen Bauteile des Balancierers sowie deren Verdrahtung mit dem Mikrocontroller dargestellt. | Als technischer Systementwurf für das Projekt wurde der folgende Verdrahtungsplan erstellt (siehe Abbildung 3). In diesem sind alle elektronischen Bauteile des Balancierers sowie deren Verdrahtung mit dem Mikrocontroller dargestellt. | ||
[[Datei:Verdrahtungsplan Kugelbalancierer .jpg|mini|left|800px| | [[Datei:Verdrahtungsplan Kugelbalancierer .jpg|mini|left|800px|Abbildung 3: Technischer Systementwurf des Balancierers]] | ||
<br clear=all> | <br clear=all> | ||
| Zeile 215: | Zeile 215: | ||
In der Neutralstellung des Servos befindet sich die Schiene waagerecht, während die Verbindungsstange senkrecht steht. Alle genannten Maße wurden im Rahmen der Gehäuseentwicklung berücksichtigt. | In der Neutralstellung des Servos befindet sich die Schiene waagerecht, während die Verbindungsstange senkrecht steht. Alle genannten Maße wurden im Rahmen der Gehäuseentwicklung berücksichtigt. | ||
Auf der folgenden Abbildung 7 die vollständige Baugruppe des Kugel-Balanciers dargestellt. | |||
{| class="mw-datatable" | {| class="mw-datatable" | ||
! style="font-weight: bold;" | | ! style="font-weight: bold;" | | ||
| Zeile 226: | Zeile 226: | ||
Ein zentraler Gedanke bei der Entwicklung des Gehäuses für den Kugel-Balancierer war ein modularer Aufbau. Das bedeutet, dass die Baugruppe aus mehreren einzelnen Komponenten besteht, die zusammen das Gesamtmodell bilden. Dadurch wird gewährleistet, dass einzelne Bauteile leicht ausgetauscht werden können und jederzeit ein einfacher Zugang zu allen wichtigen Komponenten möglich ist. | Ein zentraler Gedanke bei der Entwicklung des Gehäuses für den Kugel-Balancierer war ein modularer Aufbau. Das bedeutet, dass die Baugruppe aus mehreren einzelnen Komponenten besteht, die zusammen das Gesamtmodell bilden. Dadurch wird gewährleistet, dass einzelne Bauteile leicht ausgetauscht werden können und jederzeit ein einfacher Zugang zu allen wichtigen Komponenten möglich ist. | ||
Die Wandstärke der Bauteile beträgt in den meisten Fällen 3 mm, ein guter Kompromiss zwischen Stabilität und Materialverbrauch. Im Folgenden werden die einzelnen Komponenten sowie deren Zusammenspiel näher beschrieben. Die | Die Wandstärke der Bauteile beträgt in den meisten Fällen 3 mm, ein guter Kompromiss zwischen Stabilität und Materialverbrauch. Im Folgenden werden die einzelnen Komponenten sowie deren Zusammenspiel näher beschrieben. Die jeweils zu den Komponenten zugehörigen Abbildungen finden sich im Anschluss an diesen Abschnitt. | ||
''' | '''Grundplatte''' | ||
Das Gehäuse basiert zunächst auf | Das Gehäuse basiert zunächst auf der Grundplatte, welche als Bodenplatte für das gesamte System dient und gleichzeitig mehrere Befestigungspunkte bereitstellt. Dazu gehört unter anderem der Servomotor, der direkt auf der Grundplatte verschraubt wird. Zusätzlich ist auf der Grundplatte die von uns entwickelte Stecker-Platine befestigt. | ||
Für den Einschub der Hauptplatine ist ein Schienenmechanismus integriert. Weitere Informationen zu den Platinen folgen im Unterkapitel „Platinenentwicklung“. Ebenfalls auf der Bodenplatte befindet sich der Verbindungsturm, der den Drehpunkt für die Schiene bildet. | Für den Einschub der Hauptplatine ist ein Schienenmechanismus integriert. Weitere Informationen zu den Platinen folgen im Unterkapitel „Platinenentwicklung“. Ebenfalls auf der Bodenplatte befindet sich der Verbindungsturm, der den Drehpunkt für die Schiene bildet. | ||
| Zeile 252: | Zeile 252: | ||
Auf der Schiene ist außerdem ein IR-Abstandssensor montiert. Dafür wurde ein eigenes Sensorgehäuse entwickelt, das über Befestigungslöcher direkt mit der Schiene verschraubt wird. Auf der gegenüberliegenden Seite befindet sich eine Abdeckung, die einen statischen Hintergrund für den Sensor erzeugt. Beide Bauteile, Sensorgehäuse und Sensorabdeckung, werden im Abschnitt „Komponententest des IR-Sensors“ ausführlich erläutert, da sie aufgrund ihrer speziellen Ausgestaltung eine optimale Funktion des Sensors unterstützen. | Auf der Schiene ist außerdem ein IR-Abstandssensor montiert. Dafür wurde ein eigenes Sensorgehäuse entwickelt, das über Befestigungslöcher direkt mit der Schiene verschraubt wird. Auf der gegenüberliegenden Seite befindet sich eine Abdeckung, die einen statischen Hintergrund für den Sensor erzeugt. Beide Bauteile, Sensorgehäuse und Sensorabdeckung, werden im Abschnitt „Komponententest des IR-Sensors“ ausführlich erläutert, da sie aufgrund ihrer speziellen Ausgestaltung eine optimale Funktion des Sensors unterstützen. | ||
Nachfolgendend werden alle Abbildungen der einzelnen Komponenten dargestellt: | |||
{| class="mw-datatable" | {| class="mw-datatable" | ||
! style="font-weight: bold;" | | ! style="font-weight: bold;" | | ||
| Zeile 281: | Zeile 280: | ||
Stecker-Platine | Stecker-Platine | ||
Um die Sensoren und Aktoren bequem mit der Hauptplatine verbinden zu können, entwickelten wir zusätzlich eine zweite Platine, die im Folgenden als Stecker-Platine bezeichnet wird. Die Verbindung zwischen beiden Platinen erfolgt über eine Einschubführung und eine Kombination aus Pin-Header und Buchsenleiste. Eine schematische Darstellung des Systems zeigt die folgende Abbildung. | Um die Sensoren und Aktoren bequem mit der Hauptplatine verbinden zu können, entwickelten wir zusätzlich eine zweite Platine, die im Folgenden als Stecker-Platine bezeichnet wird. Die Verbindung zwischen beiden Platinen erfolgt über eine Einschubführung und eine Kombination aus Pin-Header und Buchsenleiste. Eine schematische Darstellung des Systems zeigt die folgende Abbildung 17. | ||
{| class="mw-datatable" | {| class="mw-datatable" | ||
| Zeile 288: | Zeile 287: | ||
|+ style = "text-align: left"| | |+ style = "text-align: left"| | ||
|- | |- | ||
|[[Datei:Platinen des Kugel-Balancierers.png|mini|links|900px| Abbildung 17: Platinen des Kugel-Balancierers]] | |[[Datei:Platinen des Kugel-Balancierers.png|mini|links|900px|Abbildung 17: Platinen des Kugel-Balancierers]] | ||
|} | |} | ||
| Zeile 299: | Zeile 298: | ||
Die Stecker-Platine liefert somit die 5-Volt-Versorgung für die Hauptplatine. Alternativ kann das System über den USB-C-Anschluss gespeist werden; jedoch dürfen USB-C-Versorgung und 9-Volt-Netzteil nicht gleichzeitig angeschlossen sein. | Die Stecker-Platine liefert somit die 5-Volt-Versorgung für die Hauptplatine. Alternativ kann das System über den USB-C-Anschluss gespeist werden; jedoch dürfen USB-C-Versorgung und 9-Volt-Netzteil nicht gleichzeitig angeschlossen sein. | ||
Im Anschluss folgen die Schaltpläne sowie die Layout-Darstellungen der beiden Platinen | Im Anschluss folgen die Schaltpläne sowie die Layout-Darstellungen der beiden Platinen auf Abbildung 18 bis 22: | ||
{| class="mw-datatable" | {| class="mw-datatable" | ||
! style="font-weight: bold;" | | ! style="font-weight: bold;" | | ||
| Zeile 319: | Zeile 318: | ||
=== Komponententest === | === Komponententest === | ||
Im | Im Rahmen dieses Kapitels wird die Funktion der einzelnen mechatronischen Hauptkomponenten des Kugel Balancierers in Simulink getestet. Dabei wurden notwendige Bibliotheken und Support Packages heruntergeladen und verwendet, welche jeweils im Text beschrieben sind. | ||
==== Servomotor ==== | ==== Servomotor ==== | ||
Zur Nutzung des Servomotors wurde das "Simulink Support Package for Arduino Hardware" verwendet. Dieses Paket stellt den Simulink Block "Standard Servo Write" zur Verfügung, welcher über eine Konstante im Bereich von 0 bis 180° angesteuert wird. Dieser Block erzeugt dann ein PWM-Signal am ausgewählten digitalen PWM-Pin (hier Pin 9, siehe Abbildung 23), um den | Zur Nutzung des Servomotors wurde das "Simulink Support Package for Arduino Hardware" verwendet. Dieses Paket stellt den Simulink Block "Standard Servo Write" zur Verfügung, welcher über eine Konstante im Bereich von 0 bis 180° angesteuert wird. Dieser Block erzeugt dann ein PWM-Signal am ausgewählten digitalen PWM-Pin (hier Pin 9, siehe Abbildung 23), um den Servomotor zu verstellen und den vorgegebenen Drehwinkel zu erreichen. | ||
[[Datei:ServoTest.jpg|mini|600px|left|Abbildung 23: Testmodell Servomotor Simulink]] | [[Datei:ServoTest.jpg|mini|600px|left|Abbildung 23: Testmodell Servomotor Simulink]] | ||
<br clear=all> | <br clear=all> | ||
Zur Funktionsprüfung des Servomotors und Simulink-Blocks wurden zuerst verschiedene Stellungen des Servomotors im Bereich von 0 bis 180° angesteuert, bevor der Servo im Gehäuse montiert wurde. Im verbauten Zustand konnte dann festgestellt werden, dass sich die Wippe bei einem Servowinkel von ca. 95° in einer ausbalancierten Stellung befindet. | |||
==== Drehgeber / Taster ==== | ==== Drehgeber / Taster ==== | ||
Um die Drehgeber | Um die Drehgeber zu testen, wurde erneut ein Simulink-Block "Digital Input Pin" des Arduino Support Packages in einem Testmodell verwendet und die Signale ausgelesen (siehe Abbildung 24 & 25). | ||
[[Datei:DrehgeberTest.jpg|mini|400px|left|Abbildung 25: Testmodell der Drehgeber]] | [[Datei:DrehgeberTest.jpg|mini|400px|left|Abbildung 25: Testmodell der Drehgeber]] | ||
| Zeile 338: | Zeile 337: | ||
<br clear=all> | <br clear=all> | ||
Leider musste während des Komponententests der Drehgeber festgestellt werden, dass die | Leider musste während des Komponententests der Drehgeber festgestellt werden, dass die zur Ausführung des PID-Reglers benötigte Schrittdauer des Simulink-Modells zu hoch ist, um die Drehgeber zuverlässig auszulesen. Drehungen der Drehgebern konnten oftmals nicht erfasst werden oder wurden übersprungen. Somit wurde sich dafür entschieden, statt der Drehgeber drei Kipptaster zu verwenden. Diese konnten aufgrund der Pinbelegung 1:1 gegen die Drehgeber ausgetauscht und im Testszenario verlässlich ausgelesen werden, ohne ein Betätigungssignal zu überspringen. Nachfolgend ist eine Messung der Taster in Abbildung 27 dargestellt. | ||
[[Datei:MessungTaster.png|mini|900px|left|Abbildung 27: Testmessung der Kipptaster]] | [[Datei:MessungTaster.png|mini|900px|left|Abbildung 27: Testmessung der Kipptaster]] | ||
<br clear=all> | <br clear=all> | ||
Hierbei kann man erkennen, dass die Signale der Kipptaster im Gegensatz zu den Drehgebern für mehrere Millisekunden an den digitalen Pins anliegen und somit in der festgelegten Schrittdauer zuverlässig auslesbar sind. | |||
==== IR-Sensor ==== | ==== IR-Sensor ==== | ||
Um den Infrarotsensor zur Distanzmessung nutzen zu können, muss zuerst eine Kalibrierung des Sensors durchgeführt werden. Dabei wurde die Spannung an verschiedenen Messpunkten auf der Schiene des Kugelbalanciers gemessen, indem die Kugel in 1-cm-Schritten von 3 cm bis 28 cm auf der Schiene positioniert wurde. Hier traten jedoch Probleme auf, da die Position der Kugel nicht zuverlässig erfasst werden konnte. Durch konstruktive Maßnahmen (siehe Abbildung 14 bis 16) konnte die Zerstreuung des Infrarotlichts maßgeblich reduziert werden. | Um den Infrarotsensor testen und zur Distanzmessung nutzen zu können, muss zuerst eine Kalibrierung des Sensors durchgeführt werden. Dabei wurde die Spannung an verschiedenen Messpunkten auf der Schiene des Kugelbalanciers gemessen, indem die Kugel in 1-cm-Schritten von 3 cm bis 28 cm auf der Schiene positioniert wurde. Hier traten jedoch Probleme auf, da die Position der Kugel nicht zuverlässig vom Sensor erfasst werden konnte, vermutlicherweise durch eine Streuung bzw. Störung des Infrarotlichts. Durch konstruktive Maßnahmen (siehe Abbildung 14 bis 16) konnte die Zerstreuung und Störung des Infrarotlichts maßgeblich reduziert werden. So konnten die Messpunkte der Kugel aufgenommen und in einer Lookup-Tabelle in Simulink verarbeitet werden. Anhand einer Umrechnung der Ausgangsspannung des Sensors anhand der Messpunkte konnte dann die aktuelle Distanz bestimmt werden. Die Messwerte sind der folgenden Tabelle zu entnehmen. | ||
{| class="wikitable" | {| class="wikitable" | ||
| Zeile 406: | Zeile 407: | ||
|} | |} | ||
Anschließend wurde eine Sprungantwort des Systems und die Distanz der Kugel ausgemessen. | Anschließend wurde eine Sprungantwort des Systems und die Distanz der Kugel ausgemessen, welche im nachfolgenden Kapitel 7.3 weiter behandelt wird. | ||
<br clear=all> | <br clear=all> | ||
| Zeile 414: | Zeile 413: | ||
==== LCD-Display ==== | ==== LCD-Display ==== | ||
Zum Auslesen des Displays wurde eine Arduino Bibliothek in Verbindung mit dem I/O-Device Builder genutzt | Zum Auslesen des Displays wurde eine Arduino Bibliothek in Verbindung mit dem I/O-Device Builder genutzt. Mithilfe des I/O-Device Blocks können Arduino Bibliotheken in Kombination mit C/C++ Code genutzt werden. So kann eine normale Textausgabe auf dem 16x2 LCD-Display mithilfe des C++-Befehls "lcd.print()" ausgegeben werden. Durch den Befehl "lcd.clear()" kann der Text auf dem Display gelöscht und mit "lcd.setCursor()" kann die Stelle des Displays ausgewählt werden, an der der Text geschrieben werden soll. Der dazugehörige Code befindet ist in Kapitel 7.4.7 LCD-Steuerung dargestellt. | ||
Mithilfe des I/O-Device Builders, der Arduino Bibliothek und dieser Befehle konnte ein Beispieltext auf das Display geschrieben und somit erfolgreich getestet werden. | |||
=== Reglerauslegung === | === Reglerauslegung === | ||
Der Kugel-Balancierer stellt ein klassisches Beispiel für ein instabiles System der Regelungstechnik dar. Im Gegensatz zu stabilen Systemen, wie etwa einer Temperaturregelung, erreicht die Kugel ohne aktiven Regeleingriff keinen statischen Endwert. Da die Erdbeschleunigung in Form der Hangabtriebskraft konstant auf die Kugel wirkt, resultiert daraus ein sogenanntes I2-Verhalten (Doppelintegrator). Physikalisch lässt sich dies dadurch erklären, dass die Position der Kugel das zweifache Zeitintegral der Beschleunigung ist: Die erste Integration führt von der Beschleunigung zur Geschwindigkeit, während die zweite Integration die zurückgelegte Distanz liefert. | Der Kugel-Balancierer stellt ein klassisches Beispiel für ein instabiles System der Regelungstechnik dar. Im Gegensatz zu stabilen Systemen, wie etwa einer Temperaturregelung, erreicht die Kugel ohne aktiven Regeleingriff keinen statischen Endwert. Da die Erdbeschleunigung in Form der Hangabtriebskraft konstant auf die Kugel wirkt, resultiert daraus ein sogenanntes I2-Verhalten (Doppelintegrator). Physikalisch lässt sich dies dadurch erklären, dass die Position der Kugel das zweifache Zeitintegral der Beschleunigung ist: Die erste Integration führt von der Beschleunigung zur Geschwindigkeit, während die zweite Integration die zurückgelegte Distanz liefert. | ||
Um dieses Verhalten mathematisch für eine Simulation in Simulink abzubilden, muss die Regelstrecke experimentell identifiziert werden. Hierzu wird eine Sprungantwort aufgenommen, indem der Servomotor im offenen Regelkreis auf einen festen Winkel gestellt wird. In diesem spezifischen Versuch wurde ein Winkel von 85° gewählt, was bei einer definierten Mittelstellung von 95° einer Neigung von Δα = 10∘ entspricht. Während die Kugel die Schiene entlangrollt, zeichnet ein Distanzsensor die Position kontinuierlich auf. | Um dieses Verhalten mathematisch für eine Simulation in Simulink abzubilden, muss die Regelstrecke experimentell identifiziert werden. Hierzu wird eine Sprungantwort aufgenommen, indem der Servomotor im offenen Regelkreis auf einen festen Winkel gestellt wird. In diesem spezifischen Versuch wurde ein Winkel von 85° gewählt, was bei einer definierten Mittelstellung von 95° einer Neigung von Δα = 10∘ entspricht. Während die Kugel die Schiene entlangrollt, zeichnet ein Distanzsensor die Position kontinuierlich auf. Dabei konnte die folgende Messung auf Abbildung 28 aufgenommen werden: | ||
[[Datei:Sprungantwort vom Kugel-Balancierer.png|mini|left|800px| | [[Datei:Sprungantwort vom Kugel-Balancierer.png|mini|left|800px|Abbildung 28: Sprungantwort des Kugel-Balancierers]] | ||
<br clear=all> | <br clear=all> | ||
Die Auswertung dieser Messdaten erfolgt über ein mathematisches Modell, bei dem ein Polynom zweiten Grades (<math>x(t)=p1\cdot t^2+p2\cdot t+p3</math>) an die Messkurve angepasst wird. Der Koeffizient <math>p1</math> dieses Polynoms entspricht dabei dem physikalischen Term <math>\frac{1}{2}a</math>. Durch einfaches Umstellen lässt sich somit die reale Beschleunigung <math>a</math> bestimmen. Um die für die Übertragungsfunktion <math>G(s) = \frac{K}{s^2}</math> benötigte Streckenverstärkung <math>K</math> zu ermitteln, wird die berechnete Beschleunigung durch den Eingangssprung dividiert. Dabei muss man den Neigungswinkel von Grad in Radiant umzurechnen. Der folgende Programmcode zeigt die Berechnung von dem K-Faktor aus der Sprungantwort mit der polyfit Funktion in Matlab: | Die Auswertung dieser Messdaten erfolgt über ein mathematisches Modell, bei dem ein Polynom zweiten Grades (<math>x(t)=p1\cdot t^2+p2\cdot t+p3</math>) an die Messkurve angepasst wird. Der Koeffizient <math>p1</math> dieses Polynoms entspricht dabei dem physikalischen Term <math>\frac{1}{2}a</math>. Durch einfaches Umstellen lässt sich somit die reale Beschleunigung <math>a</math> bestimmen. Um die für die Übertragungsfunktion <math>G(s) = \frac{K}{s^2}</math> benötigte Streckenverstärkung <math>K</math> zu ermitteln, wird die berechnete Beschleunigung durch den Eingangssprung dividiert. Dabei muss man den Neigungswinkel von Grad in Radiant umzurechnen. Der folgende Programmcode zeigt die Berechnung von dem K-Faktor aus der Sprungantwort mit der polyfit Funktion in Matlab: | ||
<div style="width:1200px; height:500px; overflow:scroll; border: hidden"> | <div style="width:1200px; height:500px; overflow:scroll; border: hidden"> | ||
<syntaxhighlight lang="cpp" style="border: none; background-color: #EFF1C1; font-size:larger"> | <syntaxhighlight lang="cpp" style="border: none; background-color: #EFF1C1; font-size:larger"> | ||
| Zeile 494: | Zeile 497: | ||
</div> | </div> | ||
Der berechnete k-Faktor beträgt 188,87 und wurde mithilfe des entsprechenden Skripts ermittelt. Die Übertragungsfunktion zur Simulation des Kugel-Balancierers lautet somit <math>G(s) = \frac{188,87}{s^2}</math> Mit dieser Übertragungsfunktion kann nun ein Regler implementiert und getestet werden. Zu diesem Zweck wurde ein Simulink-Modell aufgebaut, das in der folgenden Abbildung dargestellt ist. | Der berechnete k-Faktor beträgt 188,87 und wurde mithilfe des entsprechenden Skripts ermittelt. Die Übertragungsfunktion zur Simulation des Kugel-Balancierers lautet somit <math>G(s) = \frac{188,87}{s^2}</math> Mit dieser Übertragungsfunktion kann nun ein Regler implementiert und getestet werden. Zu diesem Zweck wurde ein Simulink-Modell aufgebaut, das in der folgenden Abbildung 29 dargestellt ist. | ||
[[Datei:Kugel Balancierer Regelstrecke Bild.png|mini|left|800px| | |||
[[Datei:Kugel Balancierer Regelstrecke Bild.png|mini|left|800px|Abbildung 29: Simulink-Modell der Regelstrecke]] | |||
<br clear=all> | <br clear=all> | ||
Die Regelparameter wurden mit diesem Modell variiert und getestet. Mit den Werten für Kp = 2, Ki = 0,2 und Kd = 0,4 entsteht | |||
[[Datei:Reglerauslegung sim.png|mini|left|800px| | Die Regelparameter wurden mit diesem Modell variiert und getestet. Mit den Werten für Kp = 2, Ki = 0,2 und Kd = 0,4 entsteht die nachfolgende Regelung: | ||
[[Datei:Reglerauslegung sim.png|mini|left|800px|Abbildung 30: Reglersimulation]] | |||
<br clear=all> | <br clear=all> | ||
Auf der obigen Abbildung kann man erkennen, dass der Regler den gewünschten Sollwert nach einem Einschwingvorgang erreicht. Somit kann diese Parameterkombination als geeignet angesehen werden, um das Ziel des Kugel Balancierers das erfolgreiche Halten der Kugel in der Mitte zu erreichen. | |||
=== Software-Umsetzung === | === Software-Umsetzung === | ||
Als erster Schritt zur Umsetzung der Software wurde ein Programm-Ablaufplan (siehe Abbildung | Als erster Schritt zur Umsetzung der Software wurde ein Programm-Ablaufplan (siehe Abbildung 31) erstellt, um die benötigten Funktionen des zu erstellenden Algorithmus schrittweise festzulegen. Nach einer Initialisierung des Systems wird die Hauptschleife des Programms ausgeführt. Zu Beginn der Schleife wird die Messspannung des IR-Sensors ausgelesen werden, um diese in eine Distanz zur Kugel umrechnen zu können. Anhand der berechneten Distanz wird die Abweichung der Kugel zur Wippenmitte bestimmt (Regelfehler). Als nächstes sollen die an den Drehgeber bzw. Taster eingestellten Parameter des PID-Reglers werden ausgelesen und auf dem Display ausgegeben werden. Der Regler berechnet dann die Stellgröße (Servowinkel), welche über ein PWM-Signal den Servomotors ansteuert und die der Wippe bewegt. Zulsetzt sorgt eine Bedingung dafür, dass eine Win-Kondition beim Halten der Kugel in der Mitte der Wippe für 5 Sekunden ausgelöst und der Gewinncode auf dem Display ausgegeben wird. | ||
[[Datei:Kugel-Balancierer.png|mini|600px|left|Abbildung | [[Datei:Kugel-Balancierer.png|mini|600px|left|Abbildung 31: Programm-Ablaufplan des Kugel-Balancierers]] | ||
<br clear=all> | <br clear=all> | ||
Das Simulink-Modell für den Kugel-Balancierer ist in mehrere Subsysteme aufgebaut, welche jeweils eine bestimmte Aufgabe übernehmen. Dieser Aufbau dient der Strukturierung der Programmierung und fördert die Wartbarkeit des Programms. Die Subsysteme wurden zuerst einzeln getestet, um anschließend die Funktion des Gesamtsystems testen zu können. Die folgende Abbildung zeigt das Gesamtmodell des Kugel-Balancierers. | Das Simulink-Modell für den Kugel-Balancierer ist in mehrere Subsysteme aufgebaut, welche jeweils eine bestimmte Aufgabe übernehmen. Dieser Aufbau dient der Strukturierung der Programmierung und fördert die Wartbarkeit des Programms. Die Subsysteme wurden zuerst einzeln getestet, um anschließend die Funktion des Gesamtsystems testen zu können. Die folgende Abbildung 32 zeigt das Gesamtmodell des Kugel-Balancierers. | ||
[[Datei:Kugel-Balancierer slx Bild.png|mini|900px|left|Abbildung | [[Datei:Kugel-Balancierer slx Bild.png|mini|900px|left|Abbildung 32: Hauptmodell des Kugel-Balancierers]] | ||
<br clear=all> | <br clear=all> | ||
| Zeile 528: | Zeile 535: | ||
==== Tasterbestimmung ==== | ==== Tasterbestimmung ==== | ||
[[Datei:Kugel-Balancierer Tasterbestimmung.png|mini|600px|left|Abbildung | |||
[[Datei:Kugel-Balancierer Tasterbestimmung.png|mini|600px|left|Abbildung 33: Tasterbestimmung Subsystem des Kugel-Balancierers]] | |||
<br clear=all> | <br clear=all> | ||
Die | |||
Die Idee hinter diesem Modell ist es, einen Zähler zu implementieren, der seinen Wert erhöht, wenn der Kipptaster nach oben gedrückt wird, und verringert, wenn der Taster nach unten gedrückt wird. | Die obige Abbildung 33 zeigt das Tasterbestimmung-Subsystem des Kugel-Balancierers. Dieses Modul wertet die Signale der Kipptaster aus, um damit die Reglerparameter zu steuern. Die Idee hinter diesem Modell ist es, einen Zähler zu implementieren, der seinen Wert erhöht, wenn der Kipptaster nach oben gedrückt wird, und verringert, wenn der Taster nach unten gedrückt wird. | ||
Zuerst werden die Tastersignale über einen digitalen Eingang in Simulink eingelesen. Anschließend werden die Signale auf eine positive Flanke überprüft. Dadurch wird sichergestellt, dass der Zählerwert nur um eins erhöht oder verringert wird, auch wenn der Taster gedrückt gehalten wird. Das bedeutet, dass der Detect-Block bei gedrücktem Taster nur für einen Zyklus ein Signal mit dem Wert 1 ausgibt. | |||
Die Signale des Kipptasters werden anschließend addiert, wobei der Taster nach unten einen Wert von −1 besitzt. Da das resultierende Signal nur für einen Zyklus anliegt, wird ein Integrator-Block verwendet, der als Zähler fungiert. | Die Signale des Kipptasters werden anschließend addiert, wobei der Taster nach unten einen Wert von −1 besitzt. Da das resultierende Signal nur für einen Zyklus anliegt, wird ein Integrator-Block verwendet, der als Zähler fungiert. | ||
Zum Schluss werden die einzelnen Parameter durch einen voreingestellten Wert dividiert, um die finalen Reglerparameter auszugeben. | Zum Schluss werden die einzelnen Parameter durch einen voreingestellten Wert dividiert, um die finalen Reglerparameter auszugeben. | ||
==== Sollwert-Modus-Bestimmung ==== | ==== Sollwert-Modus-Bestimmung ==== | ||
[[Datei:Kugel-Balancierer Sollwert-Modus-Bestimmung.png|mini|600px|left|Abbildung | |||
Auf der nachfolgenden Abbildung 34 ist das Subsystem der Sollwert- und Modus-Bestimmung des Kugel-Balancierers dargestellt. | |||
[[Datei:Kugel-Balancierer Sollwert-Modus-Bestimmung.png|mini|600px|left|Abbildung 34: Sollwert-Modus-Bestimmung Subsystem des Kugel-Balancierers]] | |||
<br clear=all> | <br clear=all> | ||
Der Kugel-Balancierer regelt die Kugel in die Mitte der Schiene. Abhängig von äußeren Einflüssen | Dieses Subsystem liest die Tastersignale aus und implementiert sowohl die Funktionalität zur Sollwertkalibrierung als auch zur Bestimmung des Betriebsmodus. Der Kugel-Balancierer regelt die Kugel in die Mitte der Schiene. Abhängig von äußeren Einflüssen (wie bspw. Lichtverhältnissen) kann es jedoch vorkommen, dass der voreingestellte Sollwert nicht mit dem tatsächlich gemessenen Mittelpunktabstand übereinstimmt. Aus diesem Grund besteht die Möglichkeit, die Mittelpunktdistanz durch Betätigung eines Tasters zu kalibrieren. Wird dieser kürzer als drei Sekunden betätigt, so wird der Betriebsmodus gewechselt. Dabei wird vom Regelmodus in den Kalibriermodus übergegangen. | ||
Im Kalibriermodus fährt die Schiene auf einen definierten Winkel. Mithilfe der Kalibrierhilfe kann die Kugel anschließend exakt in der | Im Kalibriermodus fährt die Schiene auf einen definierten Winkel. Mithilfe der Kalibrierhilfe kann die Kugel anschließend exakt in der Schienenmitte gehalten werden. Wird der Taster nun für mindestens drei Sekunden gedrückt, so wird die aktuell gemessene Distanz ausgelesen und als neuer Sollwert gespeichert. Durch dieses Vorgehen kann der Kugel-Balancierer zuverlässig auch unter unterschiedlichen äußeren Einflüssen betrieben werden. | ||
Durch dieses Vorgehen kann der Kugel-Balancierer zuverlässig auch unter unterschiedlichen äußeren Einflüssen betrieben werden. | |||
==== Distanzbestimmung ==== | ==== Distanzbestimmung ==== | ||
[[Datei:Kugel-Balancierer Distanzbestimmung.png|mini|600px|left|Abbildung | |||
Nachfolgend ist das Distanzbestimmung-Subsystem des Kugel-Balancierers dargestellt (siehe Abbildung 35). Das Modul ist dafür zuständig, die Ausgangsspannung des Sharp-IR-Sensors einzulesen. | |||
[[Datei:Kugel-Balancierer Distanzbestimmung.png|mini|600px|left|Abbildung 35: Distanzbestimmung Subsystem des Kugel-Balancierers]] | |||
<br clear=all> | <br clear=all> | ||
Bei dieser Ausgangsspannung handelt es sich um einen Analogwert im Bereich von 0 bis 1023. Der analoge Wert wird zunächst in eine entsprechende Spannung umgerechnet. Anschließend wird mithilfe der Sensorkennlinie und der gemessenen Spannung die Distanz bestimmt. Die Sensorkennlinie wurde zuvor experimentell eingemessen und in Simulink mithilfe einer Lookup-Tabelle realisiert. Die zugehörigen Kennlinienwerte wurden bereits im Kapitel Komponentenspezifikation des Sensors behandelt. | |||
Zusätzlich wird das Distanzsignal gefiltert, um ein sauberes und störungsarmes Signal für die Regelung bereitzustellen. Hierfür kommen ein Medianfilter sowie ein Tiefpassfilter zum Einsatz. Der Medianfilter dient der Eliminierung von Ausreißern, da der Sharp-IR-Sensor zu systematischen Messausreißern neigt. Zur Glättung des Signals wird anschließend ein Tiefpassfilter verwendet. | |||
Der Alpha-Parameter des Tiefpassfilters wurde experimentell mithilfe einer Open-Loop-Simulation bestimmt. | Zusätzlich wird das Distanzsignal gefiltert, um ein sauberes und störungsarmes Signal für die Regelung bereitzustellen. Hierfür kommen ein Medianfilter sowie ein Tiefpassfilter zum Einsatz. Der Medianfilter dient der Eliminierung von Ausreißern, da der Sharp-IR-Sensor zu systematischen Messausreißern neigt. Zur Glättung des Signals wird anschließend ein Tiefpassfilter verwendet. Der Alpha-Parameter des Tiefpassfilters wurde experimentell mithilfe einer Open-Loop-Simulation bestimmt. | ||
==== Regler ==== | ==== Regler ==== | ||
[[Datei:Kugel-Balancierer Regler.png|mini|600px|left|Abbildung | |||
[[Datei:Kugel-Balancierer Regler.png|mini|600px|left|Abbildung 36: Regler Subsystem des Kugel-Balancierers]] | |||
<br clear=all> | <br clear=all> | ||
Die | |||
Zu Beginn wird die Regelabweichung aus dem Sollwert und der aktuellen Distanz berechnet. Diese Regelabweichung wird anschließend dem Regler zugeführt, der anhand der drei Reglerparameter einen Stellwert berechnet. Die Reglerparameter werden über das Tasterbestimmung-Subsystem gesetzt und können während des Betriebs verändert werden. | Die obige Abbildung 36 zeigt das Regler-Subsystem des Kugel-Balancierers, welches als klassischer Regelkreis aufgebaut ist. Zu Beginn wird die Regelabweichung aus dem Sollwert und der aktuellen Distanz berechnet. Diese Regelabweichung wird anschließend dem Regler zugeführt, der anhand der drei Reglerparameter einen Stellwert berechnet. Die Reglerparameter werden über das Tasterbestimmung-Subsystem gesetzt und können während des Betriebs verändert werden. | ||
Nach der Berechnung des Stellwerts wird der Winkel der Mittelstellung addiert, da der Servo im Bereich von 0° bis 180° angesteuert wird. In der Theorie entspricht die Mittelstellung einem Winkel von 90°. Aufgrund des mechanischen Aufbaus liegt die tatsächliche Mittelstellung jedoch bei 95°. | |||
Abschließend wird der Ausgang auf die zulässigen Endwerte begrenzt. Zusätzlich wird eine Begrenzung der Änderungsrate implementiert, da der Servo nicht unendlich schnell reagieren kann. | Nach der Berechnung des Stellwerts wird der Winkel der Mittelstellung addiert, da der Servo im Bereich von 0° bis 180° angesteuert wird. In der Theorie entspricht die Mittelstellung einem Winkel von 90°. Aufgrund des mechanischen Aufbaus liegt die tatsächliche Mittelstellung jedoch bei 95°. Abschließend wird der Ausgang auf die zulässigen Endwerte begrenzt. Zusätzlich wird eine Begrenzung der Änderungsrate implementiert, da der Servo nicht unendlich schnell reagieren kann. | ||
==== Spielstatus ==== | ==== Spielstatus ==== | ||
[[Datei:Kugel-Balancierer Spielstatus.png|mini|600px|left|Abbildung | |||
[[Datei:Kugel-Balancierer Spielstatus.png|mini|600px|left|Abbildung 37: Spielstatus Subsystem des Kugel-Balancierers]] | |||
<br clear=all> | <br clear=all> | ||
Ist die Regelabweichung kleiner oder gleich 0,3 cm, zählt ein Integrator-Block hoch. Erreicht der Integrator-Block einen Wert von fünf Sekunden, wird der Spielstatus auf Sieg gesetzt und das Display gibt den Gewinncode aus. | Abbildung 37 zeigt das Spielstatus-Subsystem des Kugel-Balancierers. Dieses System überwacht den aktuellen Spielstatus. Ziel des Kugel-Balancierers ist es, die Kugel für eine bestimmte Zeit in der Mitte der Schiene zu halten. Ist die Regelabweichung kleiner oder gleich 0,3 cm, zählt ein Integrator-Block hoch. Erreicht der Integrator-Block einen Wert von fünf Sekunden, wird der Spielstatus auf Sieg gesetzt und das Display gibt den Gewinncode aus. Befindet sich die Kugel auch nur kurzzeitig außerhalb der Toleranz von 0,3 cm, wird der Integrator-Block zurückgesetzt, sodass die Zeitmessung erneut beginnt. | ||
Befindet sich die Kugel auch nur kurzzeitig außerhalb der Toleranz von 0,3 cm, wird der Integrator-Block zurückgesetzt, sodass die Zeitmessung erneut beginnt. | |||
==== Servosteuerung ==== | ==== Servosteuerung ==== | ||
[[Datei:Kugel-Balancierer Servo Steuerung.png|mini|600px|left|Abbildung | |||
Die nachfolgende Abbildung 38 zeigt das Servo-Steuerung-Subsystem des Kugel-Balancierers. | |||
[[Datei:Kugel-Balancierer Servo Steuerung.png|mini|600px|left|Abbildung 38: Servo_Steuerung Subsystem des Kugel-Balancierers]] | |||
<br clear=all> | <br clear=all> | ||
Im Normalfall wird der Servowinkel vom Regler vorgegeben. Soll jedoch der Sollwert kalibriert werden, wird nicht der vom Regler berechnete Winkel verwendet, sondern ein fester Winkel von 85° eingestellt. Dadurch kann die Kugel mithilfe der Kalibrierhilfe in der Mitte gehalten werden, sodass der neue Sollwert eingestellt werden kann. | Dieses Modell erhält einen Servowinkel als Eingang und steuert damit den Servomotor an. Im Normalfall wird der Servowinkel vom PID-Regler vorgegeben. Soll jedoch der Sollwert kalibriert werden, wird nicht der vom Regler berechnete Winkel verwendet, sondern ein fester Winkel von 85° eingestellt. Dadurch kann die Kugel mithilfe der Kalibrierhilfe in der Mitte gehalten werden, sodass der neue Sollwert eingestellt werden kann. | ||
==== LCD-Steuerung ==== | ==== LCD-Steuerung ==== | ||
| Zeile 739: | Zeile 758: | ||
=== IR-Sensor === | === IR-Sensor === | ||
Die | Die nachfolgende Abbildung 39 zeigt die berechnete Messunsicherheit des IR Sensors. | ||
[[Datei:KB Messunsicherheit IR.png|mini|800px|left|Abbildung 39: Messunsicherheit des IR-Sensors für den Kugel-Balancierer]] | |||
<br clear=all> | <br clear=all> | ||
Auf Abbildung ist die Messunsicherheit des IR-Sensors bei einer Referenzdistanz von 14,5 cm dargestellt. Aus 5 Messwerten ergibt sich ein Mittelwert von 14,5032 cm mit einer kombinierten Messunsicherheit (Typ C) von ± 0,2687 cm, was etwa 3,71 % des Mittelwerts entspricht. | |||
Die Unsicherheit Typ C setzt sich aus der statistischen Unsicherheit der Messreihe (Typ A) sowie der systematischen Unsicherheit des Messsystems (Typ B) zusammen. Alle Messwerte liegen innerhalb der berechneten Unsicherheitsgrenzen, und der Mittelwert stimmt gut mit dem Referenzwert überein. Das Messergebnis wird daher als verwertbar eingestuft. | Die Unsicherheit Typ C setzt sich aus der statistischen Unsicherheit der Messreihe (Typ A) sowie der systematischen Unsicherheit des Messsystems (Typ B) zusammen. Alle Messwerte liegen innerhalb der berechneten Unsicherheitsgrenzen, und der Mittelwert stimmt gut mit dem Referenzwert überein. Das Messergebnis wird daher als verwertbar eingestuft. | ||
| Zeile 752: | Zeile 770: | ||
Zur Bestimmung des Filterparameters α des Tiefpassfilters wurde eine Open-Loop-Simulation durchgeführt. Hierzu wurde zunächst eine ungefilterte Distanzmessung über einen definierten Zeitraum aufgezeichnet. Dieses Signal wurde anschließend gespeichert und in ein separates Simulink-Modell geladen. | Zur Bestimmung des Filterparameters α des Tiefpassfilters wurde eine Open-Loop-Simulation durchgeführt. Hierzu wurde zunächst eine ungefilterte Distanzmessung über einen definierten Zeitraum aufgezeichnet. Dieses Signal wurde anschließend gespeichert und in ein separates Simulink-Modell geladen. | ||
In diesem Modell kamen mehrere Tiefpassfilter mit unterschiedlichen Filterparametern zur Anwendung, um das Signal zu filtern. Die daraus resultierenden gefilterten Signale wurden anschließend in MATLAB ausgewertet. Die folgende Abbildung zeigt die Ergebnisse dieser Auswertung | In diesem Modell kamen mehrere Tiefpassfilter mit unterschiedlichen Filterparametern zur Anwendung, um das Signal zu filtern. Die daraus resultierenden gefilterten Signale wurden anschließend in MATLAB ausgewertet. Die folgende Abbildung 40 zeigt die Ergebnisse dieser Auswertung: | ||
[[Datei:KB Filter Openloop.png|mini|600px|left|Abb. | |||
[[Datei:KB Filter Openloop.png|mini|600px|left|Abb. 40: Ergebnisse der OpenLoop Simulation für die Tiefpassfilterauslegung]] | |||
<br clear=all> | <br clear=all> | ||
| Zeile 766: | Zeile 785: | ||
=== Projektplan === | === Projektplan === | ||
[[Datei:KB Projektplan.png|mini|1000px|links|Abbildung | Auf Abbildung 41 ist der Zeitplan dieses Projekts abgebildet, welcher die abzuarbeitenden Meilensteine zur Umsetzung des Kugel-Balancierers beinhaltet. Bei der Erstellung des Projektplans wurde sich an den einzelnen Schritten des V-Modells orientiert. | ||
[[Datei:KB Projektplan.png|mini|1000px|links|Abbildung 41: Gantt Projektplan für das Projekt "Kugel-Balancierer“]] | |||
<br clear=all> | <br clear=all> | ||
Version vom 13. Januar 2026, 02:53 Uhr
| Autoren: | Kilian Engelhardt, Daniel Block |
| Betreuer: | Prof. Schneider |
Einleitung
Das Escape Game "Kugel-Balancierer" entsteht im Rahmen des Moduls Angewandte Mechatronik des Studiengangs Business and Systems Engineering (BSE). Anhand dieses Projekts lässt sich zeigen, wie sich mit wenigen Bauteilen ein experimentelles Puzzle für ein physikalisch-technisches Escape Game entwerfen lässt. Eine Kugel rollt auf einer einachsig kippbaren Schiene, ein Servomotor verändert den Neigungswinkel, ein Distanzsensor misst die Position. Die Spielenden stellen über drei Drehregler die P-, I- und D-Anteile eines Reglers ein. Ziel ist es, die Kugel für eine definierte Zeit im Fenster um die Mittelposition zu halten – gelingt dies, wird ein Code auf dem Display ausgegeben.
Das Puzzle erinnert an klassische Murmelbahnen und vermittelt zugleich zentrale Begriffe der Regelungstechnik. Die zugrunde liegende Physik ist anschaulich: Entlang der geneigten Ebene wirkt die Beschleunigung (für kleine Winkel ), die den Kugelort verändert. Ein PID-Regler nach der Formel stabilisiert das System. Hierbei stellt der Winkel des Servomotors die Stellgröße dar, der Positionsfehler bildet die Regelgröße.
Bezüglich der Vorgehensweise bei diesem Projekt wurde sich am Ablauf des V-Modells orientiert.
Schwierigkeitslevel: fortgeschritten
Lernziele: Spielerisch die Anwendung eines Reglers und die Einflüsse der drei Anteile P, I und D erlernen
Bezug zum BSE Studium: Regelungstechnik, Messdatenverarbeitung (Filterung)
Anforderungen
Als erster Schritt nach Vorgehensweise des V-Modells wurden Anforderungen definiert, welche während der Arbeiten am Projekt des Escape Games erfüllt werden sollen.
Die Anforderungen wurden in folgende Kapitel untergliedert und in Tabelle 1 festgehalten:
- Hardware
- Komponententest
- Software
- Programmierung
- Dokumentation
| ID | Typ (I = Info, A = Anforderung) | Kapitel | Inhalt | Ersteller | Datum | Status Auftragnehmer |
| 10 | I | 1 | Hardware | |||
| 11 | A | Die Sensoren und Aktoren müssen mit dem Arduino verbunden sein. | Block | 02.10.2025 | Ausstehend | |
| 12 | A | Die Außenmaße des Kugel-Balancierers müssen kleiner als 358,02 x 250 x 250 mm sein. | Block | 02.10.2025 | Ausstehend | |
| 13 | A | Die konstruierten Bauteile sollen mittels 3D-Druck hergestellt werden, wobei der Anteil des für Stützstrukturen verwendeten Filaments weniger als 10 % des gesamten Filamentverbrauchs betragen darf. | Block | 02.10.2025 | Ausstehend | |
| 20 | I | 2 | Komponententest | |||
| 21 | A | Die Verdrahtung der elektronischen Komponenten mit dem Mikrocontroller muss mit dem Verdrahtungsplan überstimmen. | Engelhardt | 02.10.2025 | Ausstehend | |
| 22 | A | Der Distanzsensor muss die Distanz zum Ball in einem Bereich von 3 bis 30 cm messen können. | Engelhardt | 02.10.2025 | Ausstehend | |
| 23 | A | Der Distanzsensor muss eine Abtastrate von mindestens 20 Hz haben. | Engelhardt | 02.10.2025 | Ausstehend | |
| 24 | A | Der Servomotor muss die Schiene von der Mittelstellung aus um mindestens 3 cm nach oben und 3 cm nach unten bewegen können. | Engelhardt | 02.10.2025 | Ausstehend | |
| 30 | I | 3 | Software | |||
| 31 | A | Die Programmierung des Mikrocontrolleralgorithmus muss durch die MATLAB/Simulink Software in der Version 2024b erfolgen. | Engelhardt | 02.10.2025 | Ausstehend | |
| 32 | A | Der Mittelpunkt der Schiene muss mit einer Kalibrierfunktion einstellbar sein. | Engelhardt | 02.10.2025 | Ausstehend | |
| 33 | A | Die Gewinnkondition muss erreicht werden, wenn der Ball für 5 Sekunden in der Mitte der Schiene (± 1,5 cm) balanciert wird. | Engelhardt | 02.10.2025 | Ausstehend | |
| 34 | A | Der Code für das nächste Rätsel muss bei Erreichen der Gewinnkondition auf dem Display angezeigt werden. | Engelhardt | 02.10.2025 | Ausstehend | |
| 40 | I | 4 | Programmierung | |||
| 41 | A | Der Servomotor muss mit einem PWM-Signal angesteuert werden. | Block | 02.10.2025 | Ausstehend | |
| 42 | A | Eine Funktion zur Filterung falscher Messwerte muss in den Algorithmus implementiert werden. | Block | 02.10.2025 | Ausstehend | |
| 43 | A | Das PWM-Signal für den Servomotor muss von einem PID-Regler berechnet werden | Block. | 02.10.2025 | Ausstehend | |
| 44 | A | Die P-, I- und D-Anteile des Reglers müssen in Echtzeit über Drehregler einstellbar sein. | Block | 02.10.2025 | Ausstehend | |
| 45 | A | Die aktuellen Werte für die P-, I- und D-Anteile des Reglers müssen auf einem Display angezeigt werden. | Block | 02.10.2025 | Ausstehend | |
| 50 | I | 5 | Dokumentation | |||
| 51 | A | Alle Softwarekomponenten müssen einen Header besitzen. | Engelhardt | 02.10.2025 | Ausstehend | |
| 52 | A | Ein Wiki-Artikel muss nach Anleitung fertiggestellt werden. | Engelhardt | 02.10.2025 | Ausstehend | |
| 53 | A | Die angefertigten CAD-Modelle und Programmdaten müssen in SVN hochgeladen werden. | Engelhardt | 02.10.2025 | Ausstehend |
Materialliste
| Nr. | Anz. | Komponente | Beschreibung |
|---|---|---|---|
| 1 | 1 | Funduino Mega | Microcontroller |
| 2 | 1 | Sharp GP2Y0A41SK0F | Distanzsensor |
| 3 | 1 | MG996R | Servomotor |
| 4 | 3 | KY-040 | Drehregler |
| 5 | 1 | I602 I2C LCD Modul | Display |
| 6 | 1 | Taster | Taster |
| 7 | 1 | Reely Kugellager 3mm | Kugellager für Schiene |
| 8 | 1 | Gehäuse | 3D-Druck Gehäuse |
| 9 | 2 | Gabelkopf | Gabelkopf mit M3 Gewinde für Koppelstange |
| 10 | 1 | M3 Gewindestange | M3 Gewindestange für Koppelstange |
| 11 | 1 | Netzteil | 9V, 30W Netzteil |
| 12 | 1 | Diverse Verdrahtungsadern | Zum Verbinden der Komponenten |
| 13 | 1 | Diverse Schrauben | Zum Zusammenbauen der Komponenten |
Funktionaler Systementwurf
In der folgenden Abbildung 2 ist der funktionalen Systementwurf des Kugel-Balancierers dargestellt. Die mechanischen Elemente werden aus Holz bzw. mittels 3D-Druck erstellt. Mittels Servomotor kann der Drehwinkel einer Drehscheibe (Stellgröße) verändert werden, um die Laufbahn der zu balancierenden Kugel (in gelb dargestellt) zubewegen. An einer Seite der Laufbahn befindet sich ein Infrarot Distanzsensor, um die aktuelle Position dieser Kugel auf der Laufbahn zu erfassen, welche ebenfalls die Regelgröße des Systems darstellt. Diese soll durch einen auf dem Mikrocontroller (hier Arduino MEGA) ausgeführten PID Regler geregelt werden. Um das Escape Game zu starten und die P-, I- und D-Anteile des Reglers über die drei Rotary Encoder einzustellen, muss das System über den seitlichen Schalter eingeschaltet werden. Bei Erfolg wird ein Code über den Display ausgegeben.
Technischer Systementwurf
Als technischer Systementwurf für das Projekt wurde der folgende Verdrahtungsplan erstellt (siehe Abbildung 3). In diesem sind alle elektronischen Bauteile des Balancierers sowie deren Verdrahtung mit dem Mikrocontroller dargestellt.
Komponentenspezifikation
Servomotor
Der MG996R ist ein leistungsstarker Servomotor, der präzise Positionsbewegungen ausführen kann. Er wandelt PWM-Signale in eine definierte Drehstellung in Grad um und hält diese Position durch ein internes Rückkopplungssystem. Durch sein hohes Drehmoment ist der Servo in der Lage, die Wippe des Balancierers ohne Probleme zu bewegen.
- Betriebsspannung: 4,8 bis 7,2 V
- Stellkraft: 11 kg/cm bei 6,0 V
- Metallgetriebe
- 3 Pins (VCC,GND,PWM)
Infrarot-Distanzsensor
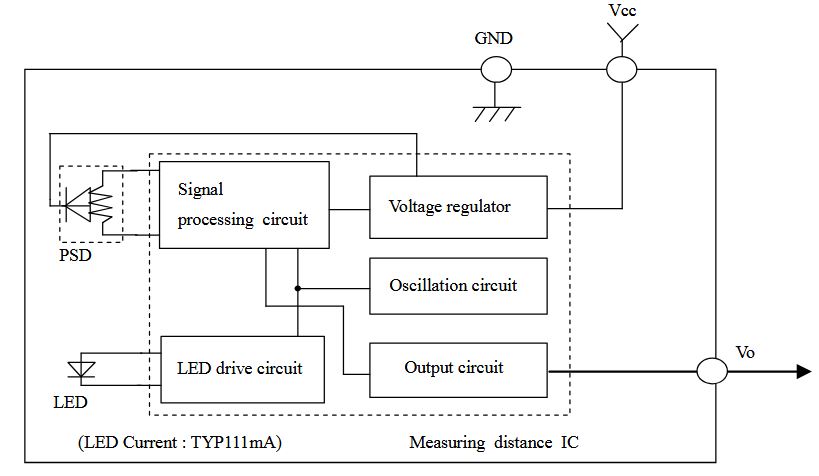
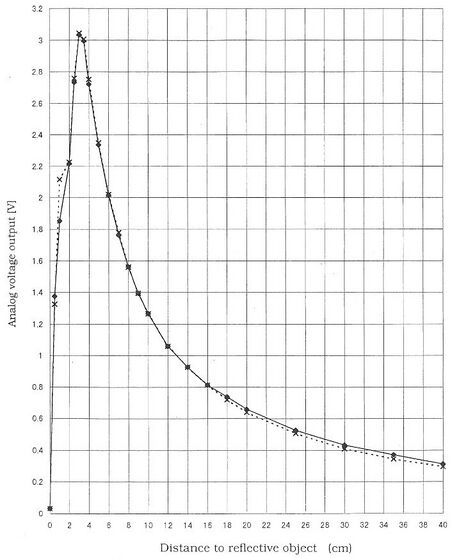
Der Sharp GP2Y0A41SK0F ist ein optischer Infrarot-Abstandssensor, der die Entfernung eines Objekts im Bereich von etwa 4 bis 30 cm messen kann. Das Messprinzip des Sensors beruht auf dem Aussenden eines Infrarotlichtstrahls mittels Infrarot LED, welcher von einem sich im Messbereich des Sensors befindlichen Objekt reflektiert und vom Detektor des Sensors (PSD, position sensitive detector) erneut aufgenommen und ausgewertet wird. In Abbildung 4 ist der Messaufbau des Distanzsensors zur Verdeutlichung dargestellt. Eine resultierende Ausgangsspannung des Sensors kann beispielhaft mithilfe der Kennlinie aus dem Sensordatenblatt (siehe Abbildung 5) in einen Abstand zum Objekt in cm umgerechnet werden, im weiteren Verlauf des Projekts wird jedoch eine eigene Sensorkalibrierung an verschiedenen Messpunkten durchgeführt.
- Betriebsspannung: 4,5 bis 5,5 V
- Messbereich: 4 bis 30 cm
- Abtastrate: ca. 60 Hz
- Pinbelegung: 3 Pins (VCC,Vo,GND)
Drehgeber
Bei den für das Projekt verwendeten Drehgebern zur Einstellung der PID-Anteile handelt es sich um die KY-040 rotary encoder. Deren wesentliche Merkmale sind nachfolgend aufgelistet:
- Betriebsspannung: 5V
- 20 Pulse pro 360° Umdrehung
- kontinuierlich drehbar
- 5 Pins (CLK,DT,Switch,VCC,GND)
Anhand der Pins CLK, DT und GND kann die Drehrichtung des Drehgebers bestimmt werden. Liegt zuerst ein High-Signal an den Pins CLK und GND an, handelt es sich um eine Drehung im Uhrzeigersinn. Wird jedoch zuerst das High-Signal zwischen den Pins DT und GND erkannt, liegt eine Drehung im Gegenuhrzeigersinn vor. [3]
LCD-Display
Als Display zur Ausgabe von bspw. Nutzeranweisungen wird ein 1602 I2C LCD Modul mit HD44780 eingesetzt. Dieses besitzt die folgenden Eigenschaften:
- Betriebsspannung: 5V
- Pinbelegung: 4 Pins (VCC, GND, SDA, SCL)
- Display besitzt blaue Hintergrundbeleuchtung und weiße Schrift
- 2 Zeichenreihen mit 16 Zeichen pro Reihe auf Display
- verlötetes I2C HD44780 Modul
Umsetzung (HW/SW)
Hardware-Umsetzung
Gehäuseentwicklung
Die Entwicklung des Gehäuses begann mit einer ersten Skizze des möglichen Aufbaus. Im Mittelpunkt stand dabei der Kippmechanismus der Schiene in Kombination mit dem Servomotor. Daher wurde zunächst dieser zentrale Mechanismus konzipiert und anschließend das restliche Gehäuse darum herum konstruiert.
Die nachfolgende Abbildung zeigt die ursprüngliche Skizze des Kugel-Balanciers, welche als Grundlage für die weitere Entwicklung des CAD-Modells diente.
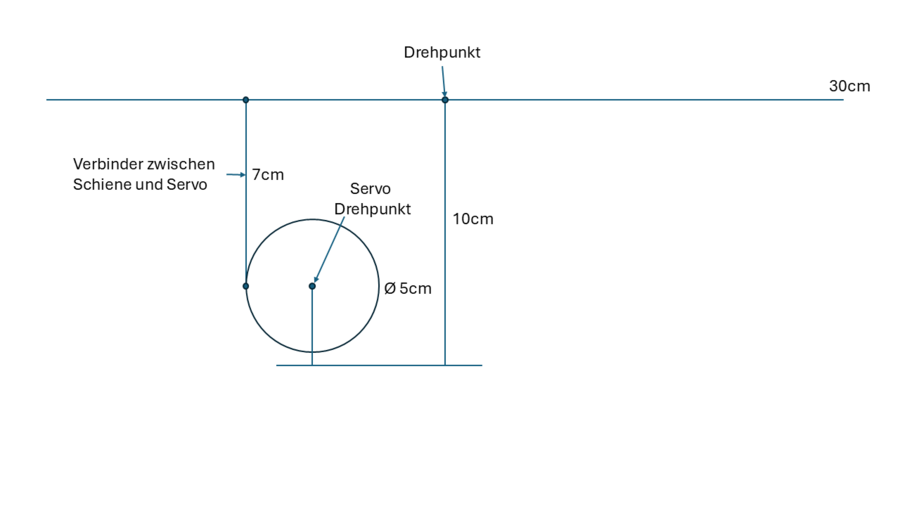 |
Die Schiene besitzt eine Länge von 30 cm, wobei sich ihr Drehpunkt exakt in der Mitte befindet. Schiene und Servomotor sind über eine Verbindungsstange miteinander gekoppelt. Der Anschlusspunkt dieser Verbindungsstange liegt 7,5 cm vom Drehpunkt der Schiene entfernt, während die Stange selbst 7 cm lang ist. Die Verbindungsstange wird über einen Servoarm mit dem Servomotor verbunden. Der Abstand zwischen dem Drehpunkt des Servos und der Anbindung der Verbindungsstange beträgt dabei 2,5 cm. In der Neutralstellung des Servos befindet sich die Schiene waagerecht, während die Verbindungsstange senkrecht steht. Alle genannten Maße wurden im Rahmen der Gehäuseentwicklung berücksichtigt.
Auf der folgenden Abbildung 7 die vollständige Baugruppe des Kugel-Balanciers dargestellt.
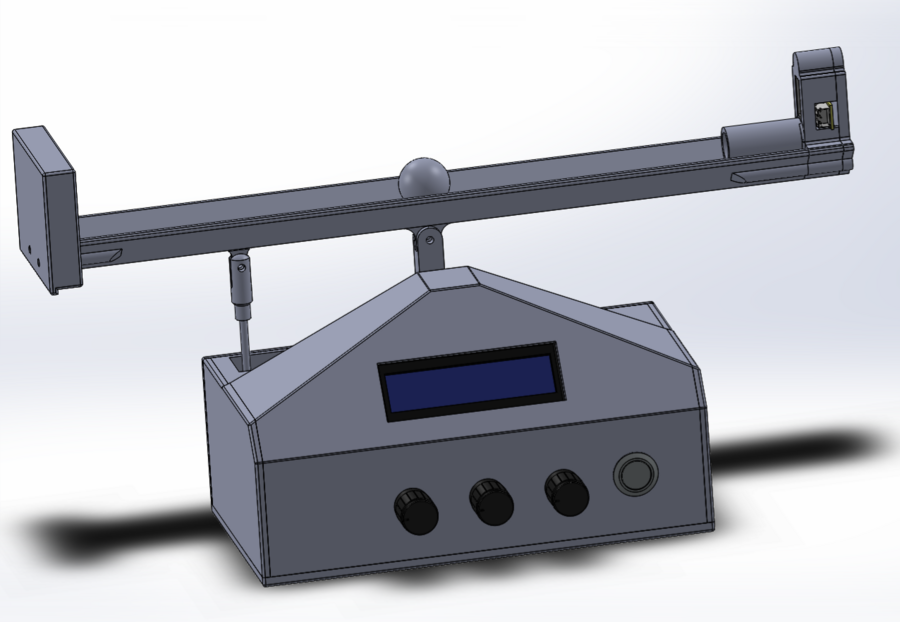 |
Ein zentraler Gedanke bei der Entwicklung des Gehäuses für den Kugel-Balancierer war ein modularer Aufbau. Das bedeutet, dass die Baugruppe aus mehreren einzelnen Komponenten besteht, die zusammen das Gesamtmodell bilden. Dadurch wird gewährleistet, dass einzelne Bauteile leicht ausgetauscht werden können und jederzeit ein einfacher Zugang zu allen wichtigen Komponenten möglich ist.
Die Wandstärke der Bauteile beträgt in den meisten Fällen 3 mm, ein guter Kompromiss zwischen Stabilität und Materialverbrauch. Im Folgenden werden die einzelnen Komponenten sowie deren Zusammenspiel näher beschrieben. Die jeweils zu den Komponenten zugehörigen Abbildungen finden sich im Anschluss an diesen Abschnitt.
Grundplatte
Das Gehäuse basiert zunächst auf der Grundplatte, welche als Bodenplatte für das gesamte System dient und gleichzeitig mehrere Befestigungspunkte bereitstellt. Dazu gehört unter anderem der Servomotor, der direkt auf der Grundplatte verschraubt wird. Zusätzlich ist auf der Grundplatte die von uns entwickelte Stecker-Platine befestigt.
Für den Einschub der Hauptplatine ist ein Schienenmechanismus integriert. Weitere Informationen zu den Platinen folgen im Unterkapitel „Platinenentwicklung“. Ebenfalls auf der Bodenplatte befindet sich der Verbindungsturm, der den Drehpunkt für die Schiene bildet.
Hauptgehäuse
Die nächste Komponente ist das Hauptgehäuse, das die äußere Hülle bildet und mit vier M3-Schrauben auf der Bodenplatte befestigt wird. Auch hier sind wieder verschiedene Bauteile integriert:
Das LCD-Display, das in einem ergonomischen Winkel angebracht ist, um ein komfortables Ablesen zu ermöglichen.
Drei Drehgeber sowie ein zusätzlicher Taster, die gemeinsam in einer Reihe unterhalb des Displays angeordnet sind.
Das Hauptgehäuse ist an beiden Seiten sowie auf der Rückseite offen. Diese Öffnungen werden mit separaten Seitenteilen verschlossen, die mithilfe von Neodym-Magneten befestigt werden. Dazu werden die Magnete sowohl im Hauptgehäuse als auch in den Seitenteilen eingesetzt. Diese modulare Bauweise ermöglicht einen besonders einfachen Zugang zum Innenraum. Über die rechte Seitenwand kann zudem direkt auf die Hauptplatine zugegriffen werden.
Schiene
Eine weitere zentrale Komponente ist die Schiene, auf der die Kugel balanciert wird. Diese ist über den Drehpunkt mit der Grundplatte verbunden, wobei ein Kugellager im Drehpunkt für eine reibungslose und spielfreie Bewegung sorgt.
Für den Neigungsmechanismus ist die Schiene über eine M3-Gewindestange mit dem Servomotor gekoppelt. An beiden Enden der Gewindestange befinden sich Gabelköpfe, welche die Verbindung zu Schiene und Servoarm herstellen.
Auf der Schiene ist außerdem ein IR-Abstandssensor montiert. Dafür wurde ein eigenes Sensorgehäuse entwickelt, das über Befestigungslöcher direkt mit der Schiene verschraubt wird. Auf der gegenüberliegenden Seite befindet sich eine Abdeckung, die einen statischen Hintergrund für den Sensor erzeugt. Beide Bauteile, Sensorgehäuse und Sensorabdeckung, werden im Abschnitt „Komponententest des IR-Sensors“ ausführlich erläutert, da sie aufgrund ihrer speziellen Ausgestaltung eine optimale Funktion des Sensors unterstützen.
Nachfolgendend werden alle Abbildungen der einzelnen Komponenten dargestellt:
Platinenentwicklung
Der Kugel-Balancierer benötigt einen Mikrocontroller, um die Sensoren und Aktoren ansteuern zu können und die erforderlichen Regelungsberechnungen durchzuführen. Wir haben uns für die Nutzung eines Arduino Mega 2560 entschieden, da dieser ausreichend Rechenleistung sowie genügend Ressourcen bietet. Allerdings wollten wir nicht das vollständige Arduino-Mega-Entwicklungsboard verwenden, da die Vielzahl an Header-Pins für unser Projekt nicht benötigt wird. Zudem bieten Steckverbindungen über klassische Pin-Header keine dauerhafte, zuverlässige Lösung und sind eher für erste Prototypen geeignet. Aus diesem Grund entschieden wir uns, eine eigene Hauptplatine zu entwickeln, auf der sich unser Mikrocontroller befindet.
Um weiterhin vollständige Kompatibilität mit dem Arduino-Framework – und damit auch die modellbasierte Programmierung mit Simulink – sicherzustellen, haben wir die wesentlichen Komponenten des Arduino Mega 2560 übernommen. Unser Mikrocontroller ist daher ein ATmega2560, ergänzt durch den originalen ATmega16U2 als USB-zu-Serial-Schnittstelle. Eine Verbesserung, die sich aus der Eigenentwicklung ergab, war die Integration eines USB-C-Anschlusses anstelle des klassischen USB-B-Ports zur Programmierung des Boards.
Für die Entwicklung des Schaltplans in Multisim und der Platinenlayouts in Ultiboard dienten die originalen Arduino-Mega-2560-Rev3-Schaltpläne als Vorlage. Das Ergebnis ist eine kompakte Hauptplatine, die funktional einem Arduino-Mega-Board entspricht, jedoch ohne die Vielzahl an Pin-Headern auskommt.
Stecker-Platine
Um die Sensoren und Aktoren bequem mit der Hauptplatine verbinden zu können, entwickelten wir zusätzlich eine zweite Platine, die im Folgenden als Stecker-Platine bezeichnet wird. Die Verbindung zwischen beiden Platinen erfolgt über eine Einschubführung und eine Kombination aus Pin-Header und Buchsenleiste. Eine schematische Darstellung des Systems zeigt die folgende Abbildung 17.
 |
Da wir beide Platinen selbst entwickeln konnten, waren wir in der Lage, die Abmessungen optimal an das vorhandene Gehäuse anzupassen und den Innenraum bestmöglich auszunutzen.
Die Stecker-Platine übernimmt neben der Signalverteilung zusätzlich die Spannungsversorgung. Der Kugel-Balancierer wird mit einem 9-Volt-Netzteil betrieben, während die Elektronik – insbesondere Hauptplatine, Sensoren und Aktoren – eine Versorgungsspannung von 5 Volt benötigt. Aus diesem Grund befindet sich auf der Stecker-Platine ein integrierter Spannungswandler mit den zugehörigen Kondensatoren und einer Schutzdiode.
Da der Servomotor kurzfristig hohe Ströme benötigt und dadurch Spannungsschwankungen verursachen kann, wurden zusätzlich spezielle Entstörmaßnahmen implementiert. Dazu zählen groß dimensionierte Elektrolytkondensatoren in unmittelbarer Nähe des Servo-Anschlusses sowie kleine Keramikkondensatoren direkt am Anschluss des IR-Abstandssensors. Diese Maßnahmen verhindern Störungen im Sensorsignal.
Die Stecker-Platine liefert somit die 5-Volt-Versorgung für die Hauptplatine. Alternativ kann das System über den USB-C-Anschluss gespeist werden; jedoch dürfen USB-C-Versorgung und 9-Volt-Netzteil nicht gleichzeitig angeschlossen sein.
Im Anschluss folgen die Schaltpläne sowie die Layout-Darstellungen der beiden Platinen auf Abbildung 18 bis 22:
Aus Ultiboard wurden anschließend die erforderlichen Gerber-Dateien exportiert, auf deren Basis die Platinen gefertigt werden konnten. Die Produktion erfolgte beim chinesischen Leiterplattenhersteller JLCPCB. Parallel dazu wurden verschiedene elektronische Komponenten bestellt.
Ein Großteil der benötigten Bauteile wurde jedoch von einem originalen Arduino Mega 2560 Rev3 ausgelötet und wiederverwendet, um Kosten zu sparen und eine vollständige Kompatibilität sicherzustellen.
Komponententest
Im Rahmen dieses Kapitels wird die Funktion der einzelnen mechatronischen Hauptkomponenten des Kugel Balancierers in Simulink getestet. Dabei wurden notwendige Bibliotheken und Support Packages heruntergeladen und verwendet, welche jeweils im Text beschrieben sind.
Servomotor
Zur Nutzung des Servomotors wurde das "Simulink Support Package for Arduino Hardware" verwendet. Dieses Paket stellt den Simulink Block "Standard Servo Write" zur Verfügung, welcher über eine Konstante im Bereich von 0 bis 180° angesteuert wird. Dieser Block erzeugt dann ein PWM-Signal am ausgewählten digitalen PWM-Pin (hier Pin 9, siehe Abbildung 23), um den Servomotor zu verstellen und den vorgegebenen Drehwinkel zu erreichen.

Zur Funktionsprüfung des Servomotors und Simulink-Blocks wurden zuerst verschiedene Stellungen des Servomotors im Bereich von 0 bis 180° angesteuert, bevor der Servo im Gehäuse montiert wurde. Im verbauten Zustand konnte dann festgestellt werden, dass sich die Wippe bei einem Servowinkel von ca. 95° in einer ausbalancierten Stellung befindet.
Drehgeber / Taster
Um die Drehgeber zu testen, wurde erneut ein Simulink-Block "Digital Input Pin" des Arduino Support Packages in einem Testmodell verwendet und die Signale ausgelesen (siehe Abbildung 24 & 25).


Leider musste während des Komponententests der Drehgeber festgestellt werden, dass die zur Ausführung des PID-Reglers benötigte Schrittdauer des Simulink-Modells zu hoch ist, um die Drehgeber zuverlässig auszulesen. Drehungen der Drehgebern konnten oftmals nicht erfasst werden oder wurden übersprungen. Somit wurde sich dafür entschieden, statt der Drehgeber drei Kipptaster zu verwenden. Diese konnten aufgrund der Pinbelegung 1:1 gegen die Drehgeber ausgetauscht und im Testszenario verlässlich ausgelesen werden, ohne ein Betätigungssignal zu überspringen. Nachfolgend ist eine Messung der Taster in Abbildung 27 dargestellt.

Hierbei kann man erkennen, dass die Signale der Kipptaster im Gegensatz zu den Drehgebern für mehrere Millisekunden an den digitalen Pins anliegen und somit in der festgelegten Schrittdauer zuverlässig auslesbar sind.
IR-Sensor
Um den Infrarotsensor testen und zur Distanzmessung nutzen zu können, muss zuerst eine Kalibrierung des Sensors durchgeführt werden. Dabei wurde die Spannung an verschiedenen Messpunkten auf der Schiene des Kugelbalanciers gemessen, indem die Kugel in 1-cm-Schritten von 3 cm bis 28 cm auf der Schiene positioniert wurde. Hier traten jedoch Probleme auf, da die Position der Kugel nicht zuverlässig vom Sensor erfasst werden konnte, vermutlicherweise durch eine Streuung bzw. Störung des Infrarotlichts. Durch konstruktive Maßnahmen (siehe Abbildung 14 bis 16) konnte die Zerstreuung und Störung des Infrarotlichts maßgeblich reduziert werden. So konnten die Messpunkte der Kugel aufgenommen und in einer Lookup-Tabelle in Simulink verarbeitet werden. Anhand einer Umrechnung der Ausgangsspannung des Sensors anhand der Messpunkte konnte dann die aktuelle Distanz bestimmt werden. Die Messwerte sind der folgenden Tabelle zu entnehmen.
| Entfernung in cm | Spannung in V |
|---|---|
| 3 | 2.341 |
| 4 | 2.268 |
| 5 | 2.243 |
| 6 | 2.048 |
| 7 | 1.799 |
| 8 | 1.623 |
| 9 | 1.461 |
| 10 | 1.31 |
| 11 | 1.207 |
| 12 | 1.109 |
| 13 | 1.031 |
| 14 | 0.9677 |
| 15 | 0.9189 |
| 16 | 0.8553 |
| 17 | 0.8162 |
| 18 | 0.7771 |
| 19 | 0.7331 |
| 20 | 0.694 |
| 21 | 0.6745 |
| 22 | 0.6354 |
| 23 | 0.5914 |
| 24 | 0.567 |
| 25 | 0.5474 |
| 26 | 0.53 |
| 27 | 0.51 |
| 28 | 0.4888 |
Anschließend wurde eine Sprungantwort des Systems und die Distanz der Kugel ausgemessen, welche im nachfolgenden Kapitel 7.3 weiter behandelt wird.
LCD-Display
Zum Auslesen des Displays wurde eine Arduino Bibliothek in Verbindung mit dem I/O-Device Builder genutzt. Mithilfe des I/O-Device Blocks können Arduino Bibliotheken in Kombination mit C/C++ Code genutzt werden. So kann eine normale Textausgabe auf dem 16x2 LCD-Display mithilfe des C++-Befehls "lcd.print()" ausgegeben werden. Durch den Befehl "lcd.clear()" kann der Text auf dem Display gelöscht und mit "lcd.setCursor()" kann die Stelle des Displays ausgewählt werden, an der der Text geschrieben werden soll. Der dazugehörige Code befindet ist in Kapitel 7.4.7 LCD-Steuerung dargestellt.
Mithilfe des I/O-Device Builders, der Arduino Bibliothek und dieser Befehle konnte ein Beispieltext auf das Display geschrieben und somit erfolgreich getestet werden.
Reglerauslegung
Der Kugel-Balancierer stellt ein klassisches Beispiel für ein instabiles System der Regelungstechnik dar. Im Gegensatz zu stabilen Systemen, wie etwa einer Temperaturregelung, erreicht die Kugel ohne aktiven Regeleingriff keinen statischen Endwert. Da die Erdbeschleunigung in Form der Hangabtriebskraft konstant auf die Kugel wirkt, resultiert daraus ein sogenanntes I2-Verhalten (Doppelintegrator). Physikalisch lässt sich dies dadurch erklären, dass die Position der Kugel das zweifache Zeitintegral der Beschleunigung ist: Die erste Integration führt von der Beschleunigung zur Geschwindigkeit, während die zweite Integration die zurückgelegte Distanz liefert.
Um dieses Verhalten mathematisch für eine Simulation in Simulink abzubilden, muss die Regelstrecke experimentell identifiziert werden. Hierzu wird eine Sprungantwort aufgenommen, indem der Servomotor im offenen Regelkreis auf einen festen Winkel gestellt wird. In diesem spezifischen Versuch wurde ein Winkel von 85° gewählt, was bei einer definierten Mittelstellung von 95° einer Neigung von Δα = 10∘ entspricht. Während die Kugel die Schiene entlangrollt, zeichnet ein Distanzsensor die Position kontinuierlich auf. Dabei konnte die folgende Messung auf Abbildung 28 aufgenommen werden:

Die Auswertung dieser Messdaten erfolgt über ein mathematisches Modell, bei dem ein Polynom zweiten Grades () an die Messkurve angepasst wird. Der Koeffizient dieses Polynoms entspricht dabei dem physikalischen Term . Durch einfaches Umstellen lässt sich somit die reale Beschleunigung bestimmen. Um die für die Übertragungsfunktion benötigte Streckenverstärkung zu ermitteln, wird die berechnete Beschleunigung durch den Eingangssprung dividiert. Dabei muss man den Neigungswinkel von Grad in Radiant umzurechnen. Der folgende Programmcode zeigt die Berechnung von dem K-Faktor aus der Sprungantwort mit der polyfit Funktion in Matlab:
Der berechnete k-Faktor beträgt 188,87 und wurde mithilfe des entsprechenden Skripts ermittelt. Die Übertragungsfunktion zur Simulation des Kugel-Balancierers lautet somit Mit dieser Übertragungsfunktion kann nun ein Regler implementiert und getestet werden. Zu diesem Zweck wurde ein Simulink-Modell aufgebaut, das in der folgenden Abbildung 29 dargestellt ist.

Die Regelparameter wurden mit diesem Modell variiert und getestet. Mit den Werten für Kp = 2, Ki = 0,2 und Kd = 0,4 entsteht die nachfolgende Regelung:

Auf der obigen Abbildung kann man erkennen, dass der Regler den gewünschten Sollwert nach einem Einschwingvorgang erreicht. Somit kann diese Parameterkombination als geeignet angesehen werden, um das Ziel des Kugel Balancierers das erfolgreiche Halten der Kugel in der Mitte zu erreichen.
Software-Umsetzung
Als erster Schritt zur Umsetzung der Software wurde ein Programm-Ablaufplan (siehe Abbildung 31) erstellt, um die benötigten Funktionen des zu erstellenden Algorithmus schrittweise festzulegen. Nach einer Initialisierung des Systems wird die Hauptschleife des Programms ausgeführt. Zu Beginn der Schleife wird die Messspannung des IR-Sensors ausgelesen werden, um diese in eine Distanz zur Kugel umrechnen zu können. Anhand der berechneten Distanz wird die Abweichung der Kugel zur Wippenmitte bestimmt (Regelfehler). Als nächstes sollen die an den Drehgeber bzw. Taster eingestellten Parameter des PID-Reglers werden ausgelesen und auf dem Display ausgegeben werden. Der Regler berechnet dann die Stellgröße (Servowinkel), welche über ein PWM-Signal den Servomotors ansteuert und die der Wippe bewegt. Zulsetzt sorgt eine Bedingung dafür, dass eine Win-Kondition beim Halten der Kugel in der Mitte der Wippe für 5 Sekunden ausgelöst und der Gewinncode auf dem Display ausgegeben wird.
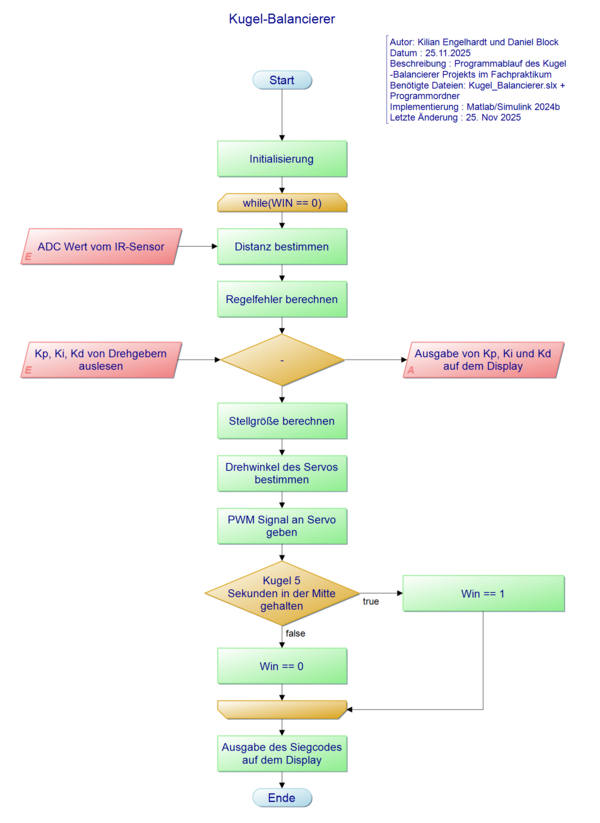
Das Simulink-Modell für den Kugel-Balancierer ist in mehrere Subsysteme aufgebaut, welche jeweils eine bestimmte Aufgabe übernehmen. Dieser Aufbau dient der Strukturierung der Programmierung und fördert die Wartbarkeit des Programms. Die Subsysteme wurden zuerst einzeln getestet, um anschließend die Funktion des Gesamtsystems testen zu können. Die folgende Abbildung 32 zeigt das Gesamtmodell des Kugel-Balancierers.

Das Modell ist in die folgenden Subsysteme aufgeteilt:
- Tasterbestimmung
- Sollwert-Modus-Bestimmung
- Distanzbestimmung
- Regler
- Spielstatus
- Servosteuerung
- LCD-Steuerung
Im Folgenden werden die einzelnen Subsysteme genauer erläutert. Dabei ist zu beachten, dass der Block LCD-Steuerung kein klassisches Subsystem ist, sondern ein selbst erstellter Block, der mithilfe des IO Device Builders erzeugt wurde.
Tasterbestimmung

Die obige Abbildung 33 zeigt das Tasterbestimmung-Subsystem des Kugel-Balancierers. Dieses Modul wertet die Signale der Kipptaster aus, um damit die Reglerparameter zu steuern. Die Idee hinter diesem Modell ist es, einen Zähler zu implementieren, der seinen Wert erhöht, wenn der Kipptaster nach oben gedrückt wird, und verringert, wenn der Taster nach unten gedrückt wird.
Zuerst werden die Tastersignale über einen digitalen Eingang in Simulink eingelesen. Anschließend werden die Signale auf eine positive Flanke überprüft. Dadurch wird sichergestellt, dass der Zählerwert nur um eins erhöht oder verringert wird, auch wenn der Taster gedrückt gehalten wird. Das bedeutet, dass der Detect-Block bei gedrücktem Taster nur für einen Zyklus ein Signal mit dem Wert 1 ausgibt.
Die Signale des Kipptasters werden anschließend addiert, wobei der Taster nach unten einen Wert von −1 besitzt. Da das resultierende Signal nur für einen Zyklus anliegt, wird ein Integrator-Block verwendet, der als Zähler fungiert. Zum Schluss werden die einzelnen Parameter durch einen voreingestellten Wert dividiert, um die finalen Reglerparameter auszugeben.
Sollwert-Modus-Bestimmung
Auf der nachfolgenden Abbildung 34 ist das Subsystem der Sollwert- und Modus-Bestimmung des Kugel-Balancierers dargestellt.

Dieses Subsystem liest die Tastersignale aus und implementiert sowohl die Funktionalität zur Sollwertkalibrierung als auch zur Bestimmung des Betriebsmodus. Der Kugel-Balancierer regelt die Kugel in die Mitte der Schiene. Abhängig von äußeren Einflüssen (wie bspw. Lichtverhältnissen) kann es jedoch vorkommen, dass der voreingestellte Sollwert nicht mit dem tatsächlich gemessenen Mittelpunktabstand übereinstimmt. Aus diesem Grund besteht die Möglichkeit, die Mittelpunktdistanz durch Betätigung eines Tasters zu kalibrieren. Wird dieser kürzer als drei Sekunden betätigt, so wird der Betriebsmodus gewechselt. Dabei wird vom Regelmodus in den Kalibriermodus übergegangen.
Im Kalibriermodus fährt die Schiene auf einen definierten Winkel. Mithilfe der Kalibrierhilfe kann die Kugel anschließend exakt in der Schienenmitte gehalten werden. Wird der Taster nun für mindestens drei Sekunden gedrückt, so wird die aktuell gemessene Distanz ausgelesen und als neuer Sollwert gespeichert. Durch dieses Vorgehen kann der Kugel-Balancierer zuverlässig auch unter unterschiedlichen äußeren Einflüssen betrieben werden.
Distanzbestimmung
Nachfolgend ist das Distanzbestimmung-Subsystem des Kugel-Balancierers dargestellt (siehe Abbildung 35). Das Modul ist dafür zuständig, die Ausgangsspannung des Sharp-IR-Sensors einzulesen.

Bei dieser Ausgangsspannung handelt es sich um einen Analogwert im Bereich von 0 bis 1023. Der analoge Wert wird zunächst in eine entsprechende Spannung umgerechnet. Anschließend wird mithilfe der Sensorkennlinie und der gemessenen Spannung die Distanz bestimmt. Die Sensorkennlinie wurde zuvor experimentell eingemessen und in Simulink mithilfe einer Lookup-Tabelle realisiert. Die zugehörigen Kennlinienwerte wurden bereits im Kapitel Komponentenspezifikation des Sensors behandelt.
Zusätzlich wird das Distanzsignal gefiltert, um ein sauberes und störungsarmes Signal für die Regelung bereitzustellen. Hierfür kommen ein Medianfilter sowie ein Tiefpassfilter zum Einsatz. Der Medianfilter dient der Eliminierung von Ausreißern, da der Sharp-IR-Sensor zu systematischen Messausreißern neigt. Zur Glättung des Signals wird anschließend ein Tiefpassfilter verwendet. Der Alpha-Parameter des Tiefpassfilters wurde experimentell mithilfe einer Open-Loop-Simulation bestimmt.
Regler

Die obige Abbildung 36 zeigt das Regler-Subsystem des Kugel-Balancierers, welches als klassischer Regelkreis aufgebaut ist. Zu Beginn wird die Regelabweichung aus dem Sollwert und der aktuellen Distanz berechnet. Diese Regelabweichung wird anschließend dem Regler zugeführt, der anhand der drei Reglerparameter einen Stellwert berechnet. Die Reglerparameter werden über das Tasterbestimmung-Subsystem gesetzt und können während des Betriebs verändert werden.
Nach der Berechnung des Stellwerts wird der Winkel der Mittelstellung addiert, da der Servo im Bereich von 0° bis 180° angesteuert wird. In der Theorie entspricht die Mittelstellung einem Winkel von 90°. Aufgrund des mechanischen Aufbaus liegt die tatsächliche Mittelstellung jedoch bei 95°. Abschließend wird der Ausgang auf die zulässigen Endwerte begrenzt. Zusätzlich wird eine Begrenzung der Änderungsrate implementiert, da der Servo nicht unendlich schnell reagieren kann.
Spielstatus

Abbildung 37 zeigt das Spielstatus-Subsystem des Kugel-Balancierers. Dieses System überwacht den aktuellen Spielstatus. Ziel des Kugel-Balancierers ist es, die Kugel für eine bestimmte Zeit in der Mitte der Schiene zu halten. Ist die Regelabweichung kleiner oder gleich 0,3 cm, zählt ein Integrator-Block hoch. Erreicht der Integrator-Block einen Wert von fünf Sekunden, wird der Spielstatus auf Sieg gesetzt und das Display gibt den Gewinncode aus. Befindet sich die Kugel auch nur kurzzeitig außerhalb der Toleranz von 0,3 cm, wird der Integrator-Block zurückgesetzt, sodass die Zeitmessung erneut beginnt.
Servosteuerung
Die nachfolgende Abbildung 38 zeigt das Servo-Steuerung-Subsystem des Kugel-Balancierers.

Dieses Modell erhält einen Servowinkel als Eingang und steuert damit den Servomotor an. Im Normalfall wird der Servowinkel vom PID-Regler vorgegeben. Soll jedoch der Sollwert kalibriert werden, wird nicht der vom Regler berechnete Winkel verwendet, sondern ein fester Winkel von 85° eingestellt. Dadurch kann die Kugel mithilfe der Kalibrierhilfe in der Mitte gehalten werden, sodass der neue Sollwert eingestellt werden kann.
LCD-Steuerung
Der folgende Programmcode zeigt die LCD_Steuerung des Kugel-Balancierers. Dieser Block wurde mithilfe des IO Device Builders erstellt. Als Unterstützung diente ein Erklärvideo von Prof. Göbel auf seinem YouTube-Kanal [4]. In diesem Block wird eine Arduino-Bibliothek verwendet, um ein 16×2-LCD-Display in Simulink ansteuern zu können. Im Spielbetrieb werden die drei Regelparameter des PID-Reglers auf dem Display angezeigt. Wird vom Spielbetrieb in den Kalibriermodus gewechselt, so wird dieser Moduswechsel ebenfalls auf dem Display dargestellt. Sollte der Sollwert geändert werden, erscheint zusätzlich eine entsprechende Meldung auf dem Display. Tritt schließlich die Siegbedingung ein, indem die Kugel für die vorgegebene Zeit in der Mitte gehalten wird, so wird eine Siegesmeldung zusammen mit einem Code auf dem Display ausgegeben.
Messtechnik
Im Rahmen der Messtechnik wird die Messunsicherheit der eingesetzten Sensoren (hier IR-Distanzsensor) bestimmt, um Aussagen über die Genauigkeit und Zuverlässigkeit der Messergebnisse von Sensoren treffen zu können. Die Bestimmung der Messungenauigkeit eines Messsystems besteht aus Wiederholungsmessungen mit anschließender Berechnung der Standardabweichung und kombinierten Standardunsicherheit aus den Messwerten.
IR-Sensor
Die nachfolgende Abbildung 39 zeigt die berechnete Messunsicherheit des IR Sensors.

Auf Abbildung ist die Messunsicherheit des IR-Sensors bei einer Referenzdistanz von 14,5 cm dargestellt. Aus 5 Messwerten ergibt sich ein Mittelwert von 14,5032 cm mit einer kombinierten Messunsicherheit (Typ C) von ± 0,2687 cm, was etwa 3,71 % des Mittelwerts entspricht.
Die Unsicherheit Typ C setzt sich aus der statistischen Unsicherheit der Messreihe (Typ A) sowie der systematischen Unsicherheit des Messsystems (Typ B) zusammen. Alle Messwerte liegen innerhalb der berechneten Unsicherheitsgrenzen, und der Mittelwert stimmt gut mit dem Referenzwert überein. Das Messergebnis wird daher als verwertbar eingestuft.
Filterauslegung des Tiefpassfilters
Zur Bestimmung des Filterparameters α des Tiefpassfilters wurde eine Open-Loop-Simulation durchgeführt. Hierzu wurde zunächst eine ungefilterte Distanzmessung über einen definierten Zeitraum aufgezeichnet. Dieses Signal wurde anschließend gespeichert und in ein separates Simulink-Modell geladen.
In diesem Modell kamen mehrere Tiefpassfilter mit unterschiedlichen Filterparametern zur Anwendung, um das Signal zu filtern. Die daraus resultierenden gefilterten Signale wurden anschließend in MATLAB ausgewertet. Die folgende Abbildung 40 zeigt die Ergebnisse dieser Auswertung:

Auf Grundlage dieser Ergebnisse wurde ein Filterparameter von α = 0,3 gewählt, da sowohl die Signalglättung als auch die entstehende Verzögerung für die vorliegende Anwendung geeignet sind.
Ergebnis
Zusammenfassung
Lessons Learned
Projektunterlagen
Projektplan
Auf Abbildung 41 ist der Zeitplan dieses Projekts abgebildet, welcher die abzuarbeitenden Meilensteine zur Umsetzung des Kugel-Balancierers beinhaltet. Bei der Erstellung des Projektplans wurde sich an den einzelnen Schritten des V-Modells orientiert.
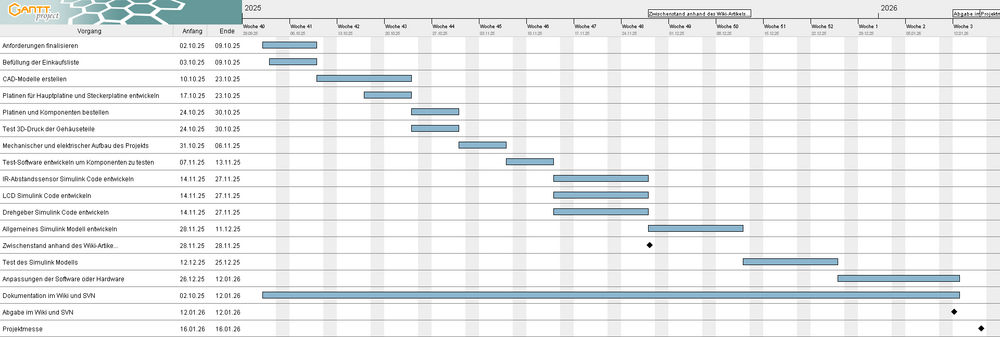
YouTube Video
Weblinks
Literatur
→ zurück zur Übersicht: WS 25/26: Escape Game













