Simulation der IR-Einparksensorik: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
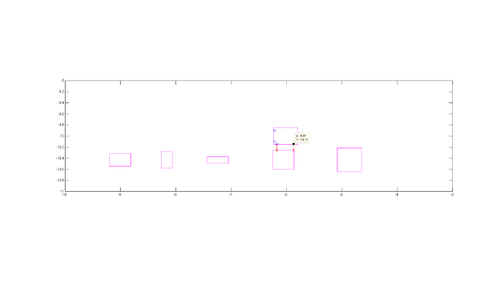
[[Datei:Position6 Sensor RechtsVorne.PNG | [[Datei:Position6 Sensor RechtsVorne.PNG|thumb|rechts|500px|LM35DZ]] | ||
→ zurück zur Übersicht: [[SDE-Team_2019/20]]<br/> | → zurück zur Übersicht: [[SDE-Team_2019/20]]<br/> | ||
Version vom 18. Juni 2019, 11:24 Uhr
→ zurück zur Übersicht: SDE-Team_2019/20
Autor: Yanick Christian Tchenko
Betreuer: Prof. Schneider
Aufgabenstellung zum zweiten Meilenstein
- Übertragen der Testsoftware aus dem Branch in den Trunk (erledigt)
- Vereinfachung von Abstandssensorik.m. Für einen beliebigen IR-Sensor soll eine Funktion erstellt werden. Diese Funktion wird für alle 4 Sensoren aufgerufen. (erledigt)
- Code Review durch Prof. Schneider (erledigt)
- Test der neuen Unterfunktion (erledigt)
- Zeitmessung: Darstellung der Verbesserung, Optimierung durch mex-Compiler (offen)
- Anschauliche Dokumentation der Funktion von Abstandssensorik.m I(in Arbeit)
- Nach erfolgreichem Test: Übertragung in Offline-Simulation (offen)
Allgemeine Einleitung
Zur richtigen Durchführung des Einparkmanövers müssen die Sensorpositionen sowie die Messberechnungen der Abstände zu bestehen Hindernissen richtig durchgeführt werden. Für die verschiedenen Berechnungen und Positionsfestlegungen wird im Rahmen dieses Praktikums die Funktion abstandsensorik.m (ähnlich wie die Funktion fcn.m) angewendet.
Beschreibung der ursprünglichen Funktion Abstandssensorik.m
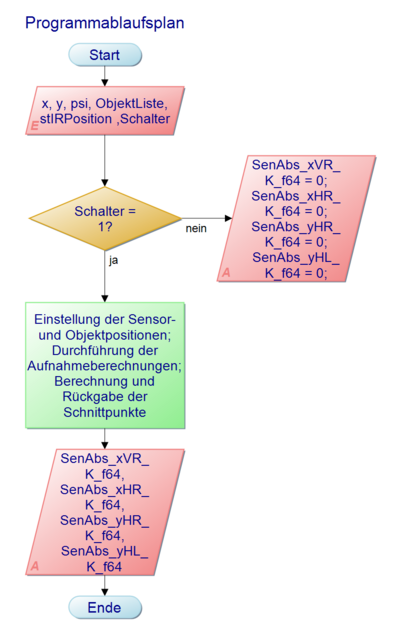
<br\>
Die ursprüngliche Funktion zur Abstand-Sensorik lässt sich wie auf der rechts stehenden Abbildung strukturell darstellen.
Zur Initialisierung der Funktion werden neben den Eingabeparametern auch Globalvariablen vordefiniert.
- Globalvariablen<br\> Diese Variablen werden an unterschiedlichen Stellen im ganzen Programmablauf angewendet. Dazu zählen hauptsächlich die Variablen zur Fahrzeugparameterdarstellung, die der Quellcode im unteren Bereich veranschaulicht.
global Geraden Geraden2 Ergebnis % Debug
global x_fahrzeug y_fahrzeug % Debug
global PAR_CAR_Fahrzeugbreite_f64
global PAR_CAR_Fahrzeuglaenge_f64
breite = PAR_CAR_Fahrzeugbreite_f64;
laenge = PAR_CAR_Fahrzeuglaenge_f64;
Fahrzeuglänge, -breite, sowie Fahrzeugkoordinaten und entsprechende Granden lassen sich hiermit deklarieren
- Inputsgrößen
x, y, psi, ObjektListe, stIRPosition ,Schalter
%% Ermittlung der Abstände zu den Hindernissen als Ausgang
if Schalter == 1 % PAR_SenAbs_Schalter_EIN_bit Rechnung durchführen, sonst nicht
% Fahrt im unteren Bereich
Winkeloffset = 180;
...
%% Bearbeitung der Objekt- und Sensorpositionen
...
%% Sensorpositionen (in m)
% IR_Sensor x-Position y-Position
% rechts vorne - 7 cm -12 cm
% rechts hinten -37 cm -12 cm
% hinten links -42 cm 10 cm
% hinten rechts -42 cm -10 cm
% Beifahrerseite
PAR_IR_xVR_x = stIRPosition(1,1); % Pos x - IR rechts vorne im Fahrzeug K-System
PAR_IR_xVR_y = stIRPosition(1,2); % Pos y
PAR_IR_xHR_x = stIRPosition(2,1); % Pos x - IR rechts hinten im Fahrzeug K-System
PAR_IR_xHR_y = stIRPosition(2,2); % Pos y
% Hecksensoren
PAR_IR_yHR_x = stIRPosition(3,1); % Pos x - IR hinter rechts im Fahrzeug K-System
PAR_IR_yHR_y = stIRPosition(3,2); % Pos y
PAR_IR_yHL_x = stIRPosition(4,1); % Pos x - IR hinter links im Fahrzeug K-System
PAR_IR_yHL_y = stIRPosition(4,2); % Pos y
ESM_psi_f64 = psi; % Fahrzeugwinkel in rad
ESM_x_I_f64 = x; % Fahrzeugposition x
ESM_y_I_f64 = y; % Fahrzeugposition y
...
...
%% Geraden des Objektes
r1 = [ObjektKante_1(1,1);ObjektKante_1(2,1)]; % Punkt auf Gerade g1
u1 = ObjektKante_2-ObjektKante_1; % Richtung
n1 = [u1(2);-u1(1)]/norm(u1); % Normal der Richtung
r2 = [ObjektKante_2(1,1);ObjektKante_2(2,1)]; % Punkt auf Gerade g2
u2 = ObjektKante_3-ObjektKante_2; % Richtung
n2 = [u2(2);-u2(1)]/norm(u2); % Normal der Richtung
r3 = [ObjektKante_3(1,1);ObjektKante_3(2,1)]; % Punkt auf Gerade g3
u3 = ObjektKante_4-ObjektKante_3; % Richtung
n3 = [u3(2);-u3(1)]/norm(u3); % Normal der Richtung
r4 = [ObjektKante_4(1,1);ObjektKante_4(2,1)]; % Punkt auf Gerade g4
u4 = ObjektKante_1-ObjektKante_4; % Richtung
n4 = [u4(2);-u4(1)]/norm(u4); % Normal der Richtung
...
...
%% Geraden der Sensoren
...
...
N1 = [n1' ; n_IR_VR']; % Normalvektor g1
N3 = [n3' ; n_IR_VR']; % Normalvektor g3
N4 = [n4' ; n_IR_VR']; % Normalvektor g4
b = [dot(n1,r1) ; dot(n2,r2) ; dot(n3,r3) ; dot(n4,r4) ; dot(nF,[rF(1,1);rF(2,1)])]; % Skalarprodukt ,Konstanten der Geraden
...
%% Berechnung der Schnittstelle
% Berechnung Ortsvektor Schnittpunkt IR_VR auf g3
...
...
%% Berechnungen der Schnittpunkte zwischen Sensorstrahlungen und Hindernissen
...
...
%% Rückmelden der Werte
% Seitliche Sensoren
SenAbs_xVR_K_f64 = min(alle_Abstaende_VR);
SenAbs_xHR_K_f64 = min(alle_Abstaende_HR);
% Hecksensoren
SenAbs_yHR_K_f64 = min(alle_Abstaende_yHR);
SenAbs_yHL_K_f64 = min(alle_Abstaende_yHL);
else
SenAbs_xVR_K_f64 = 0;
SenAbs_xHR_K_f64 = 0;
SenAbs_yHR_K_f64 = 0;
SenAbs_yHL_K_f64 = 0;
end
Bei diesem Code wiederholen sich die Berechnungen für die 4 Sensoren in jedem Durchgang (Positionsbestimmung, Bestimmung des Normalvektors, Bestimmung der Abstände, Schnittpunkte ...). Dies führt zu einer Erweiterung der Funktion Abstandssensorik.m (ca. 500 Programmlinien), welche weiterhin immer unübersichtlicher und somit schwieriger zu verstehen ist. Diese Problematik lässt sich jedoch teilweise beheben, wenn man Gebracht von modularer Programmgestaltung macht, wie im unteren Abschnitt mit der gleichen Funktion durchgeführt wurde.
Implementierte Vereinfachungen
Zur Übersichtlichkeit des Programmcodes wurden Vereinfachungen hauptsächlich an drei Stellen durchgeführt, wo sich die Berechnungsformeln ähneln. Man kam demnach auf die drei unteren Funktionen, deren Funktionsweisen und Aufrufsorte im Gesamtprogramm im Folgenden detailliert beschrieben stehen. <br\>
(Hinweis: Die verschiedenen Variablen hier sind zwar teilweise den im Programm angewendeten Variablen - rIR_VR und u_IR_yHR, ...- ähnlich, verbleiben jedoch durch unterschiedliche Variablendefinition und Funktionsinputs beliebig ersetzbar)
Funktion NVektoren.m
In dieser Funktion werden die Berechnungen der Ortsvektoren und der Schnittpunkte durchgeführt
function [N1, N2, N3, N4, b, r_HR_1, r_HR_2, r_HR_3, r_HR_4, r_yHL_3, bs_1, bs_2, bs_3, bs_4, bs_5]= NVektoren(n1,r1, n2,r2, n3, r3, n4, r4,nF, rF,rIR_HR, n_IR_yHL)
N1 = [n1' ; n_IR_yHL']; % Normalvektor g1
N2 = [n2' ; n_IR_yHL']; % Normalvektor g2
N3 = [n3' ; n_IR_yHL']; % Normalvektor g3
N4 = [n4' ; n_IR_yHL']; % Normalvektor g4
b = [dot(n1,r1) ; dot(n2,r2) ; dot(n3,r3);dot(n4,r4);dot(nF,[rF(1,1);rF(2,1)])]; % Skalarprodukt ,Konstanten der Geraden
%% Vergleich der Eingangsnamen zur Auswahl der durchzuführenden Aktion
s = inputname(12);
A = 'n_IR_yHL';
B = 'n_IR_yHR'
%% HR und HL-Sensoren
%% Beide Hecksensoren besitzen gleiche Berechnungsformeln, werden dementsprechend unter der gleichen Voraussetzung in der Funktion bearbeitet
if ((strcmp(s,A)== 1)|(strcmp(s,B)== 1))
if (abs(n3'*n_IR_yHL) == 1) % Parallele Vektoren
r_yHL_3 = [Inf; Inf]; % Warning: Matrix is singular to working precision.
bs_5 = 0;
else
bs_5 = [dot(n3,r3) ; dot(n_IR_yHL,[rIR_yHL(1,1);rIR_yHL(2,1)])];
r_yHL_3 = N3 \ bs_5; % Gleichung N*r=b r*n=c Berechnung Ortsvektor Schnittpunkt IR_yHR auf g1
end
r_HR_1= 0;
r_HR_2 = 0;
r_HR_3 = 0;
r_HR_4 = 0;
bs_1 = 0;
bs_2 = 0;
bs_3 = 0;
bs_4 = 0;
end
Beide vordere Sensoren besitzen gleiche Berechnungsformeln, werden dementsprechend unter der gleichen Voraussetzung in der Funktion bearbeitet
%% VR und HR-Sensoren
C = 'n_IR_VR';
D = 'n_IR_HR';
if ((strcmp(s,C)== 1)|(strcmp(s,D)== 1))
if (abs(n1'*n_IR_yHL) == 1) % Parallele Vektoren
r_HR_1 = [Inf; Inf]; % Warning: Matrix is singular to working precision.
bs_1 =0;
else
bs_1 = [dot(n1,r1) ; dot(n_IR_yHL,[rIR_HR(1,1);rIR_HR(2,1)])];
r_HR_1 = N1 \ bs_1; % Gleichung N*r=b r*n=c Berechnung Ortsvektor Schnittpunkt IR_HR auf g1
end
if (abs(n2'*n_IR_yHL) == 1) % Parallele Vektoren
r_HR_2 = [Inf; Inf]; % Warning: Matrix is singular to working precision.
bs_2 = 0;
else
bs_2 = [dot(n2,r2) ; dot(n_IR_yHL,[rIR_HR(1,1);rIR_HR(2,1)])];
r_HR_2 = N2 \ bs_2; % Gleichung N*r=b r*n=c Berechnung Ortsvektor Schnittpunkt IR_HR auf g1
end
if (abs(n3'*n_IR_yHL) == 1) % Parallele Vektoren
r_HR_3 = [Inf; Inf]; % Warning: Matrix is singular to working precision.
bs_3 = 0;
else
bs_3 = [dot(n3,r3) ; dot(n_IR_yHL,[rIR_HR(1,1);rIR_HR(2,1)])];
r_HR_3 = N3 \ bs_3; % Berechnung Ortsvektor Schnittpunkt IR_HR auf g3
end
if (abs(n4'*n_IR_yHL) == 1) % Parallele Vektoren
r_HR_4 = [Inf; Inf]; % Warning: Matrix is singular to working precision.
bs_4 = 0;
else
bs_4 = [dot(n4,r4) ; dot(n_IR_yHL,[rIR_HR(1,1);rIR_HR(2,1)])];
r_HR_4 = N4 \ bs_4; % Berechnung Ortsvektor Schnittpunkt IR_HR auf g4
end
r_yHL_3 = 0
bs_5 =0;
end
end
Funktion Objekt_Geraden.m
Diese Funktion ist eine Verallgemeinerung zur Positionsbestimmung der verschiedenen Sensoren (Vorderlinks-, Vorderrechts- sowie linke und rechte Hecksensoren). Ferner ermöglicht die Funktion die Einstellungen der Strahlrichtungen.
%% In dieser Funktion werden die Positionen der verschiednen Sensoren behandelt
function [r, u, n, rIR_VR, u_IR_yHR, n_IR_VR, rIR_VR_1, u_IR_VR_1, n_IR_VR_1] = Objekt_Geraden(ObjektKante1, ObjektKante2,ESM_x_I_f64, ESM_y_I_f64,...
Fahrzeug_Rotation,PAR_IR_xVR_x,PAR_IR_xVR_y,ESM_psi_f64)
Einnstellung der vorderen und hinteren Sensoren
r = [ObjektKante1(1,1);ObjektKante1(2,1)];% Punkt auf Gerade
u = ObjektKante2-ObjektKante1; % Richtung
n = [u(2);-u(1)]/norm(u); % Normal der Richtung
Einstellung der rechten Sensoren
rIR_VR = [[ESM_x_I_f64;ESM_y_I_f64;0]+Fahrzeug_Rotation*[PAR_IR_xVR_x;PAR_IR_xVR_y;0]]; % Montagepunkt Sensor
u_IR_yHR = [-cos(ESM_psi_f64);-sin(ESM_psi_f64)]; % Richtung
n_IR_VR = [u_IR_yHR(2);-u_IR_yHR(1)]; % Normal der Richtung
Einstellung der linken Hecksensoren
rIR_VR_1 = [[ESM_x_I_f64;ESM_y_I_f64;0]+Fahrzeug_Rotation*[PAR_IR_xVR_x;PAR_IR_xVR_y;0]]; % Montagepunkt Sensor
u_IR_VR_1 = [sin(ESM_psi_f64);-cos(ESM_psi_f64)]; % Richtung
n_IR_VR_1 = [u_IR_VR_1(2);-u_IR_VR_1(1)]; % Normal der Richtung
Funktion KoordinatenNaechsten_Schnittpunkts.m
Es werden in dieser Funktion de verschiedenen Schnittpunkte auf Sensorstrahlwegen berechnet, sowie die entsprechenden Abstände und Koordinaten. Darauf basiert wird die Entscheidung darüber getroffen, ob der Sensor ein Hindernis in seiner Reichweite erkannt hat oder nicht.
Verbesserung der Funktion
Optimierung der neuen Funktion durch die mex-Funktion
Detaillierte Informationen zur Anwendung des Mex-Compilers sind unter folgendem Link zu finden <br\> AEP_-_Autonomes_Einparken
Gegenüberstellung Ausführungszeiten der neuen und alten Funktionen
Zusammenfassung
Die Funktion abstandssensorik.m umfasst das Kernstück der Simulation der Einpark-Sensorik und auch des Einparkmanövers. Ich verständliche Darstellung, was das hauptsächliche Ziel der Aufgabestellung war, vereinfacht nicht nur die Arbeit mit dem Programm, sodern sie ermöglicht auch gewünschte Umstellungen ohne ausführliche Auseinandersetzung mit dem Quelltext und ohne den ganzen Quellcode bei fehlerhaften Umstellungen zu beeinträchtigen.
Testdurchführung: Ansatz mit der entwickelten Test-GUI
Integration in die Offline-Simulation
Literatur
→ zurück zur Übersicht: SDE-Team_2019/20