Kamera: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „'''Autor:''' Junjie Lyu <br/> '''Betreuer:''' Prof. Schneider<br/> ==Einleitung== In diesem Artikel w…“ |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
'''Autor:''' [[Benutzer:Junjie_Lyu | Junjie Lyu]] <br/> | '''Autor:''' [[Benutzer:Junjie_Lyu | Junjie Lyu]] [[Benutzer:Changlai Bao | Changlai Bao]]<br/> | ||
'''Betreuer:''' [[Benutzer:Ulrich_Schneider| Prof. Schneider]]<br/> | '''Betreuer:''' [[Benutzer:Ulrich_Schneider| Prof. Schneider]]<br/> | ||
| Zeile 34: | Zeile 34: | ||
==Offline Modell== | ==Offline Modell== | ||
In der Abbildung 1 wird die Offline Modell der Kamera beschrieben. | |||
[[Bild: Offline_Modell_Kamera.png|800px|thumb|center|Abbildung 1: Offline Modell Kamera]] | |||
==Online Modell== | ==Online Modell== | ||
Aktuelle Version vom 16. April 2022, 19:30 Uhr
Autor: Junjie Lyu Changlai Bao
Betreuer: Prof. Schneider
Einleitung
In diesem Artikel wird ein Spurpolynom des Carolo Cup Fahrzeugs beschrieben. Daher befasst sich dieser Artikel mit der Berechnung des Spurpolynoms.
Regressionsanalyse[1]
Anleitung
Ziel der Regressionsanalyse am häugigsten ist es, Beziehung zwischen einer abhängigen und einer oder mehreren unabhängigen Variable festzustellen, um ein Vorhersagemodell zu erstellen. Wenn nun zusätzliche Werte x ohne zugehörigen Wert y vorliegen, dann kann das angepasste Modell zur Vorhersage des Wertes von y verwendet werden.
Polynomische Regression
Im Falle der polynomischen Regression vom Grad 2 wird die Funktion unter der Bedingung gesucht, dass die Funktion
der Summe der Quadrate der Abstände der tatsächlichen y-Werte von berechneten -Werten ein Minimum hat.
Zur Bestimmung der Konstanten in Gleichung (1) werden die partiellen Ableitungen , und gleich null gesetzt, um jeweils das minimum zu erhalten:
Partielle Ableitung nach : dividiert durch ergibt:
Partielle Ableitung nach :
dividiert durch ergibt:
Partielle Ableitung nach :
dividiert durch ergibt:
Es entsteht wieder ein lineares Gleichungssystem in drei Variablen ,dessen Lösung die optimalen Konstanten liefert:
Offline Modell
In der Abbildung 1 wird die Offline Modell der Kamera beschrieben.
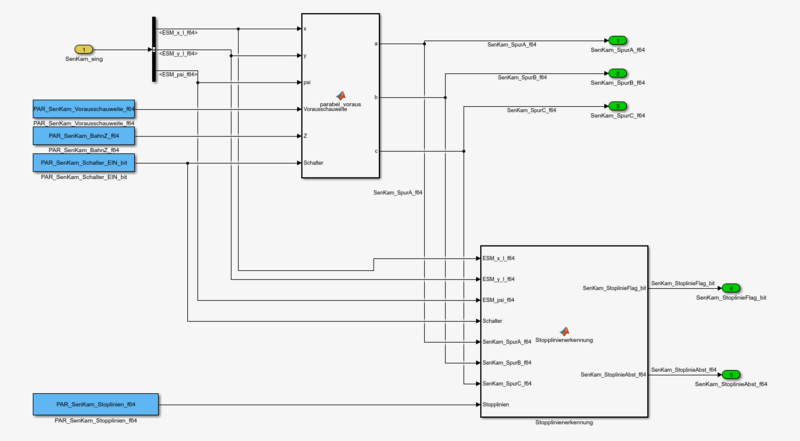
Online Modell
Literatur
→ zurück zum übergeordneten Artikel: Systemarchitektur des Fahrzeugs
→ zurück zum Hauptartikel: Praktikum SDE