Lidar Objekterkennung mit Matlab/Simulink und EV3: Unterschied zwischen den Versionen
| (43 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
→ zurück zum Hauptartikel: [[SigSys_SoSe2017| Signalverarbeitende Systeme SoSe2017]] | → zurück zum Hauptartikel: [[SigSys_SoSe2017| Signalverarbeitende Systeme SoSe2017]] | ||
== Lidar == | == Lidar == | ||
Ein Lidar (Abkürzung für engl. ''light detection and ranging'') ist ein Verfahren bzw. ein Gerät zur Ortung von Objekten. Basis hierfür | Ein Lidar (Abkürzung für engl. ''light detection and ranging'') ist ein Verfahren bzw. ein Gerät zur Ortung von Objekten. Basis hierfür bildet die Messung der Reflexion eines gepulsten Laserstrahls in Abhängigkeit von der Zeit nach dessen Aussendung oder die Messung der Phasenverschiebung der Reflexion und der daraus berechenbaren Entfernung.<ref>[http://www.spektrum.de/lexikon/physik/lidar/9033], Spektrum.de - Lexikon der Physik - Lidar. Abgerufen am 18.05.2017.</ref> | ||
=== Puls-Laufzeitverfahren === | === Puls-Laufzeitverfahren === | ||
Bei der Laufzeitmessung wird ein Lichtpuls ausgesandt. | Bei der Laufzeitmessung wird ein Lichtpuls ausgesandt. | ||
Als Pulslaufzeit wird die Zeit bezeichnet, die ein Lichtstrahl benötigt um zur Quelle zurückreflektiert zu werden. Durch Messen dieser Laufzeit <math>\Delta t</math> kann über die Lichtgeschwindigkeit | Als Pulslaufzeit wird die Zeit bezeichnet, die ein Lichtstrahl benötigt, um zur Quelle zurückreflektiert zu werden. Durch Messen dieser Laufzeit <math>\Delta t</math> kann über die Lichtgeschwindigkeit <math>c</math> die Distanz <math>r</math> zwischen Lichtquelle und Objekt ermittelt werden. Zusätzlich muss ein Faktor von 0,5 in die Rechnung mit einfließen, da der Lichtstrahl die Entfernung zweimal (hin und zurück) überwinden muss. | ||
Der Vorteil dieses Verfahrens ist die geringe Reaktionszeit. Ein großer Nachteil hingegen ist, dass die Messung selbst in sehr kurzen Zeitabständen (Nano- bis Picosekunden) erfolgen muss. Daher ist eine Messung im Nahbereich (wenige Zentimeter) problematisch und der Fehler ist verhältnismäßig groß. <ref>Mitschrift der Vorlesung ''Signalverarbeitende Systeme'' am 29.06.2017 von Prof. Dr.-Ing. Ulrich Schneider im Studiengang ''Business and Systems Engineering'' an der Hochschule Hamm-Lippstadt.</ref> | |||
<math> r = 0{,}5 \cdot c \cdot \Delta t </math> | |||
=== Phasenverschiebungsverfahren === | |||
[[Bild:Phase.PNG|thumb|200px|right|Phase einer harmonischen Schwingung]] | |||
[[Bild:Phasenverschiebung.PNG|thumb|200px|right|Phasenverschiebung ohne Dämpfung]] | |||
Aus der Reflexion eines ausgesandten Lichtstrahls kann die Phasenverschiebung ermittelt werden, denn diese ist entfernungsabhängig. Im Rückschluss kann auch über die Phasenverschiebung die zurückgelegte Distanz eines Lichtstrahls ermittelt werden. Der Brechungsindex <math>n</math> sorgt insgesamt für eine Dämpfung des Signals. | |||
Die Phasendifferenz wird folgendermaßen berechnet: | |||
<math>\phi = \frac{\Delta t}{T} \cdot 2\pi</math> | |||
Die Distanz berechnet sich dementsprechend durch: | |||
<math>r = \frac{c \cdot T}{4 \pi} \cdot (\phi + 2\pi \cdot n) = \frac{c}{2} \cdot (n \cdot T + \Delta t)</math> | |||
< | Ein Vorteil dieser Methode im Vergleich zum Laufzeitverfahren liegt in der höheren Auflösung, die mit vergleichsweise kleinem messtechnischen Aufwand realisiert werden kann. Ein Problem stell allerdings die Messentfernung dar, da der Laser kontinuierlich bei kleiner Leistung arbeitet und somit die maximale Messentfernung kleiner ist. Ein weiteres Problem stellt die Eindeutigkeit des Signals dar. Das Signal kann dabei ein Vielfaches der halben Laserwellenlänge annehmen, wodurch die Phasenverschiebung ebenfalls ein Vielfaches ist, diese aber nicht eindeutig differenziert werden kann. <ref>Jörg Hoffmann: Taschenbuch der Messtechnik, 7. Auflage, Carl Hanser Verlag München, 2015. </ref> | ||
== Hokuyo URG-04LX-UG01 == | |||
[[Bild:Scan_Radius.PNG|thumb|300px|right|Scan-Radius des Lidars]] | [[Bild:Scan_Radius.PNG|thumb|300px|right|Scan-Radius des Lidars]] | ||
Der URG-04LX ist ein Laserscanner für Flächen. Die Lichtquelle des Sensors ist ein Infrarotlaser mit 785 nm (Laserklasse 1). Der Scanbereich ist | Der URG-04LX ist ein Laserscanner für Flächen. Die Lichtquelle des Sensors ist ein Infrarotlaser mit 785 nm (Laserklasse 1). Der Scanbereich ist ein Halbkreis von 240° mit einem maximalen Radius von 4.000 mm. Der Abtastwinkel zwischen zwei Werten beträgt 0,36°. Insgesamt beträgt die Auflösung auf den Scanbereich 683 Schritte. Der Durchmesser des Lasers ist bei einer Entfernung von 2.000 mm höchstens 20 mm, die maximale Abweichung beträgt 40 mm bei 4.000 mm. | ||
Grundlage für die Distanzmessung bildet die Messung der Phasenverschiebung | Grundlage für die Distanzmessung bildet die Messung der '''Phasenverschiebung'''. <ref>[http://www.robotshop.com/media/files/pdf/hokuyo-urg-04lx-ug01-specifications.pdf], Scanning Laser Range Finder URG-04LX-UG01 Specifications - PDF. Abgerufen am 18.05.2017.</ref> | ||
{| class="wikitable" | {| class="wikitable" | ||
| Zeile 32: | Zeile 57: | ||
| Lichtquelle || Laser (max. 0,8 mW) der Klasse 1 mit λ = 785 nm | | Lichtquelle || Laser (max. 0,8 mW) der Klasse 1 mit λ = 785 nm | ||
|- | |- | ||
| Detektierungsbereich || | | Detektierungsbereich || messbarer Bereich: 20 - 5.600 mm, idealer Bereich: 60 - 4.095 mm | ||
|- | |- | ||
| Auflösung || 1 mm | | Auflösung || 1 mm | ||
| Zeile 40: | Zeile 65: | ||
| Winkelbeschleunigung || <math> \pi/2 \;{rad/\mathrm{s}^{2}}</math> | | Winkelbeschleunigung || <math> \pi/2 \;{rad/\mathrm{s}^{2}}</math> | ||
|} | |} | ||
== Implementierung in Matlab == | == Implementierung in Matlab == | ||
| Zeile 49: | Zeile 77: | ||
Mithilfe von Funktionen des Treibers kann eine serielle Verbindung über USB mit dem Lidar aufgebaut werden. Hierfür muss der richtige COM-Port in das Skript <code>run.m</code> eingetragen und anschließend ausgeführt werden. Am Ende der Initialisierung wird die Funktion <code>main_EV3.m</code> aufgerufen, | Mithilfe von Funktionen des Treibers kann eine serielle Verbindung über USB mit dem Lidar aufgebaut werden. Hierfür muss der richtige COM-Port in das Skript <code>run.m</code> eingetragen und anschließend ausgeführt werden. Am Ende der Initialisierung wird die Funktion <code>main_EV3.m</code> aufgerufen, | ||
die den kontinuierlich auszuführende Programmcode enthält. In jedem Zyklus der <code>main</code> | die den kontinuierlich auszuführende Programmcode enthält. In jedem Zyklus der <code>main</code> wird die Funktion <code>LidarScan()</code> aufgerufen, die für das Empfangen der Daten des Sensors verantwortlich ist. Die Funktion selbst nutzt die Funktion <code>decodeSCIP()</code>, um die empfangenen Daten zu dekodieren. Diese Informationen werden dann in einem Array gespeichert, aus dem anschließend die Abstandswerte in 0,36°-Intervallschritten gelesen werden können. | ||
| Zeile 96: | Zeile 124: | ||
stop(mymotor) % Motor stoppen | stop(mymotor) % Motor stoppen | ||
end | end | ||
%........................................................................% | %........................................................................% | ||
% Code zur Erkennung des Tastendrucks in der Mitte des EV3 zum Beenden des | % Code zur Erkennung des Tastendrucks in der Mitte des EV3 zum Beenden des | ||
| Zeile 117: | Zeile 147: | ||
</div> | </div> | ||
== Ergebnis == | |||
[[Bild:Foto.jpg|thumb|right|220px|Lego EV3 mit Lidar]] | |||
Der minimale messbare Abstand des Lidars liegt bei 20 cm. Wurden 20 cm als Grenze zur Vollbremsung gewählt, ist das Auto effektiv zwischen 5 und 25 cm zum Stehen gekommen. Auf der einen Seite hängt das mit dem eben beschriebenen minimalen Messabstand zusammen, zum anderen rollt das Auto auch noch einige Zentimeter nach, da der Motor lediglich ausgestellt wird und kein direktes Abbremsen erfolgt. | |||
Aus diesem Grund ist die Grenze auf 25 cm hochgesetzt worden, wodurch das Auto effektiv zwischen 15 und 25 cm anhält. | |||
Die Dateien sind im SVN hinterlegt: https://svn.hshl.de/svn/BSE_SigSys/trunk/User/Kohorte_04_SoSe17/Nora_Werner/ | |||
== Video == | |||
Zur anschaulichen Demonstration ist ein [https://youtu.be/xO1Zi-K_a-g Video] verfügbar. | |||
== Verwendete Support Packages für Matlab == | == Verwendete Support Packages für Matlab == | ||
| Zeile 122: | Zeile 165: | ||
* [https://de.mathworks.com/matlabcentral/fileexchange/57425-matlab-driver-for-hokuyu-urg-family MATLAB Driver for Hokuyu URG family] | * [https://de.mathworks.com/matlabcentral/fileexchange/57425-matlab-driver-for-hokuyu-urg-family MATLAB Driver for Hokuyu URG family] | ||
* [https://de.mathworks.com/matlabcentral/fileexchange/45075-simulink-support-package-for-lego-mindstorms-ev3-hardware Simulink (and Matlab) Support Package for LEGO MINDSTORMS EV3 Hardware] | * [https://de.mathworks.com/matlabcentral/fileexchange/45075-simulink-support-package-for-lego-mindstorms-ev3-hardware Simulink (and Matlab) Support Package for LEGO MINDSTORMS EV3 Hardware] | ||
== Einzelnachweise == | == Einzelnachweise == | ||
<references /> | <references /> | ||
---- | |||
→ zurück zum Hauptartikel: [[SigSys_SoSe2017| Signalverarbeitende Systeme SoSe2017]] | |||
Aktuelle Version vom 18. Juni 2018, 19:23 Uhr
Autor: Nora Werner
Betreuer: Prof. Dr.-Ing. Ulrich Schneider
→ zurück zum Hauptartikel: Signalverarbeitende Systeme SoSe2017
Lidar
Ein Lidar (Abkürzung für engl. light detection and ranging) ist ein Verfahren bzw. ein Gerät zur Ortung von Objekten. Basis hierfür bildet die Messung der Reflexion eines gepulsten Laserstrahls in Abhängigkeit von der Zeit nach dessen Aussendung oder die Messung der Phasenverschiebung der Reflexion und der daraus berechenbaren Entfernung.[1]
Puls-Laufzeitverfahren
Bei der Laufzeitmessung wird ein Lichtpuls ausgesandt. Als Pulslaufzeit wird die Zeit bezeichnet, die ein Lichtstrahl benötigt, um zur Quelle zurückreflektiert zu werden. Durch Messen dieser Laufzeit kann über die Lichtgeschwindigkeit die Distanz zwischen Lichtquelle und Objekt ermittelt werden. Zusätzlich muss ein Faktor von 0,5 in die Rechnung mit einfließen, da der Lichtstrahl die Entfernung zweimal (hin und zurück) überwinden muss. Der Vorteil dieses Verfahrens ist die geringe Reaktionszeit. Ein großer Nachteil hingegen ist, dass die Messung selbst in sehr kurzen Zeitabständen (Nano- bis Picosekunden) erfolgen muss. Daher ist eine Messung im Nahbereich (wenige Zentimeter) problematisch und der Fehler ist verhältnismäßig groß. [2]
Phasenverschiebungsverfahren
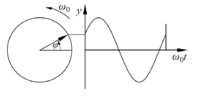
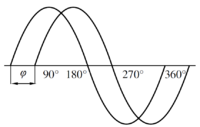
Aus der Reflexion eines ausgesandten Lichtstrahls kann die Phasenverschiebung ermittelt werden, denn diese ist entfernungsabhängig. Im Rückschluss kann auch über die Phasenverschiebung die zurückgelegte Distanz eines Lichtstrahls ermittelt werden. Der Brechungsindex sorgt insgesamt für eine Dämpfung des Signals.
Die Phasendifferenz wird folgendermaßen berechnet:
Die Distanz berechnet sich dementsprechend durch:
Ein Vorteil dieser Methode im Vergleich zum Laufzeitverfahren liegt in der höheren Auflösung, die mit vergleichsweise kleinem messtechnischen Aufwand realisiert werden kann. Ein Problem stell allerdings die Messentfernung dar, da der Laser kontinuierlich bei kleiner Leistung arbeitet und somit die maximale Messentfernung kleiner ist. Ein weiteres Problem stellt die Eindeutigkeit des Signals dar. Das Signal kann dabei ein Vielfaches der halben Laserwellenlänge annehmen, wodurch die Phasenverschiebung ebenfalls ein Vielfaches ist, diese aber nicht eindeutig differenziert werden kann. [3]
Hokuyo URG-04LX-UG01
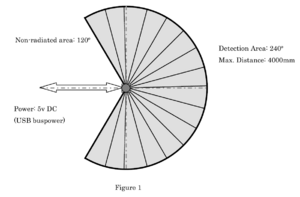
Der URG-04LX ist ein Laserscanner für Flächen. Die Lichtquelle des Sensors ist ein Infrarotlaser mit 785 nm (Laserklasse 1). Der Scanbereich ist ein Halbkreis von 240° mit einem maximalen Radius von 4.000 mm. Der Abtastwinkel zwischen zwei Werten beträgt 0,36°. Insgesamt beträgt die Auflösung auf den Scanbereich 683 Schritte. Der Durchmesser des Lasers ist bei einer Entfernung von 2.000 mm höchstens 20 mm, die maximale Abweichung beträgt 40 mm bei 4.000 mm. Grundlage für die Distanzmessung bildet die Messung der Phasenverschiebung. [4]
| Bezeichnung | Spezifikation |
|---|---|
| Lichtquelle | Laser (max. 0,8 mW) der Klasse 1 mit λ = 785 nm |
| Detektierungsbereich | messbarer Bereich: 20 - 5.600 mm, idealer Bereich: 60 - 4.095 mm |
| Auflösung | 1 mm |
| Winkelgeschwindigkeit | 360°/s |
| Winkelbeschleunigung |
Implementierung in Matlab
Matlab-Treiber für das URG-04LX Lidar
Quelle des Treibers: MATLAB Driver for Hokuyo URG family
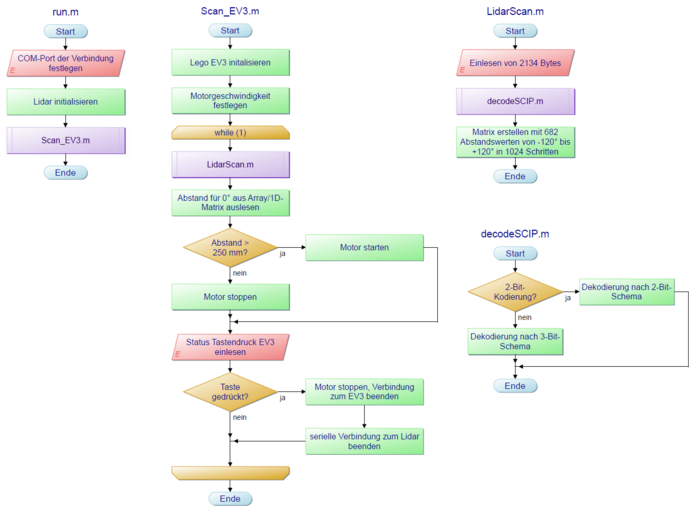
Mithilfe von Funktionen des Treibers kann eine serielle Verbindung über USB mit dem Lidar aufgebaut werden. Hierfür muss der richtige COM-Port in das Skript run.m eingetragen und anschließend ausgeführt werden. Am Ende der Initialisierung wird die Funktion main_EV3.m aufgerufen,
die den kontinuierlich auszuführende Programmcode enthält. In jedem Zyklus der main wird die Funktion LidarScan() aufgerufen, die für das Empfangen der Daten des Sensors verantwortlich ist. Die Funktion selbst nutzt die Funktion decodeSCIP(), um die empfangenen Daten zu dekodieren. Diese Informationen werden dann in einem Array gespeichert, aus dem anschließend die Abstandswerte in 0,36°-Intervallschritten gelesen werden können.
Programmierung der Funktion main_EV3 in Matlab
%........................................................................%
% Code zur Kollisionserkennung eines Lego EV3 mit einem URG-Lidar %
% %
% Das Lidar hat eine Winkelauflösung von 1024 Abstufungen auf 360°. Der %
% Abstand wird von Schritt 44 bis 725 gemessen (-120° bis 120°). Da für %
% dieses Projekt lediglich der Abstand zu einem Hindernis direkt vor %
% dem Lidar entscheidend ist, wird der Abstand nur für 0° bzw. Schritt %
% 384 benötigt. %
% %
% Autor von 'Scan_EV3.m': Nora Werner %
%........................................................................%
function main_EV3
global A lidar
%........................................................................%
%Lego Mindstorm konfigurieren
mylego = legoev3('usb') % Verbindung auf USB festlegen
beep(mylego) % kurzes akustisches Signal
mymotor = motor(mylego,'A') % Motor an Port A des EV3
mymotor.Speed = -50 % Motorgeschwindigkeit auf 50% des Maximums
%........................................................................%
% Code für die Kollisionserkennung des Lego EV3 mit einem URG-Lidar
while (1)
[A] = LidarScan(lidar); % Abstandswerte in Array/1D-Matrix schreiben
abstand = A(384) % Abfrage der Distanz zum Hindernis bei 0°
if abstand > 250 % Vergleich Abstandsgrenze zum Objekt (in mm)
start(mymotor) % Motor starten
else
stop(mymotor) % Motor stoppen
end
%........................................................................%
% Code zur Erkennung des Tastendrucks in der Mitte des EV3 zum Beenden des
% Programms
button = readButton(mylego,'center');
if button == 1
% Motoren stoppen und Verbindung zum EV3 beenden
beep(mylego)
stop(mymotor)
clear mylego
% serielle Verbindung zum Lidar trennen und Lidar ausschalten
fprintf(lidar,'QT');
fclose(lidar);
close all;
end
end
end
Ergebnis

Der minimale messbare Abstand des Lidars liegt bei 20 cm. Wurden 20 cm als Grenze zur Vollbremsung gewählt, ist das Auto effektiv zwischen 5 und 25 cm zum Stehen gekommen. Auf der einen Seite hängt das mit dem eben beschriebenen minimalen Messabstand zusammen, zum anderen rollt das Auto auch noch einige Zentimeter nach, da der Motor lediglich ausgestellt wird und kein direktes Abbremsen erfolgt.
Aus diesem Grund ist die Grenze auf 25 cm hochgesetzt worden, wodurch das Auto effektiv zwischen 15 und 25 cm anhält.
Die Dateien sind im SVN hinterlegt: https://svn.hshl.de/svn/BSE_SigSys/trunk/User/Kohorte_04_SoSe17/Nora_Werner/
Video
Zur anschaulichen Demonstration ist ein Video verfügbar.
Verwendete Support Packages für Matlab
- MATLAB Driver for Hokuyu URG family
- Simulink (and Matlab) Support Package for LEGO MINDSTORMS EV3 Hardware
Einzelnachweise
- ↑ [1], Spektrum.de - Lexikon der Physik - Lidar. Abgerufen am 18.05.2017.
- ↑ Mitschrift der Vorlesung Signalverarbeitende Systeme am 29.06.2017 von Prof. Dr.-Ing. Ulrich Schneider im Studiengang Business and Systems Engineering an der Hochschule Hamm-Lippstadt.
- ↑ Jörg Hoffmann: Taschenbuch der Messtechnik, 7. Auflage, Carl Hanser Verlag München, 2015.
- ↑ [2], Scanning Laser Range Finder URG-04LX-UG01 Specifications - PDF. Abgerufen am 18.05.2017.
→ zurück zum Hauptartikel: Signalverarbeitende Systeme SoSe2017