NXT Lichtsensor mit Matlab/Simulink

Signalverarbeitungskette eines Lego Mindstorms NXT/EV3 Lichtsensor 9844 und auslesen in Matlab Simulink

Einleitung

Der folgende Artikel befasst sich mit der Inbetriebnahme eines NXT-Lichtsensors und dem Auslesen bzw. Verarbeiten der Daten in Matlab. Entstanden ist der Artikel im Rahmen der Vorlesung Signalverarbeitende Systeme im Sommersemester 2018. Zunächst werden die Grundlagen zur Arbeit mit dem Sensor beschrieben und daraufhin umgesetzt. In diesem Artikel wird der Begriff Lego-Einheit immer durch ein LE abgekürzt.

Projektplanung

Abb. 2: Projektplanung

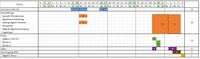
Für die Umsetzung des Projektes können maximal 1.5 CP erreicht werden. Damit stehen ca. 45 Stunden für das Projekt zur Verfügung. Damit ein ausreichender Puffer vorhanden ist, wurde mit 61 Stunden gerechnet. Mit Hilfe von Excel wurde ein Projektplan erstellt, der die Aufwände für die einzelnen Teilbereiche zeigen soll. Nach der Erstellung der Projektplanung wurde mit der Literaturrecherche gestartet. Die Auswahl des Primärsensor und die Beschreibung des ADU werden zunächst begonnen und nach einer Projektpause gemeinsam mit der Ausarbeitung der weiteren Kapitel bearbeitet. Um die an den Arduino gelieferten Daten zu verifizieren wird auch ein Test mit dem EV3 und der EV3-Software simuliert. Messungen zu den beiden Betriebsmodi und die Videoerstellung werden ebenfalls geplant.

Auswahl des Primärsensors

Funktionsweise des Sensors

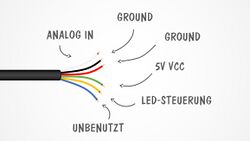
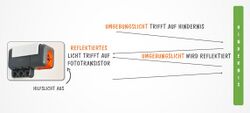
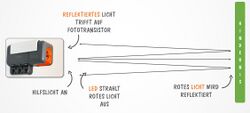
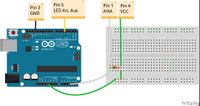
Der Lego Lichtsensor besteht aus einer roten LED mit Vorwiderstand, sowie einem Phototransistor mit Arbeitswiderstand. Der Lichtsensor kann in zwei verschiedenen Betriebsmodi benutzt werden. Im ersten Modus ist die LED ausgeschaltet. Der Phototransistor agiert als Empfänger und nimmt die vom Umgebungslicht reflektierten Strahlen des da-vorstehenden Gegenstandes auf. Je nach Intensität der eingehenden Strahlung, verändert sich die Gleichspannung im Phototransistor. Für den zweiten Betriebsmodus wird die rote LED dazugeschaltet. Die LED ist dabei in die gleiche Richtung ausgerichtet, wie der Phototransistor. Deshalb kann die LED ein Hilfslicht ausstrahlen, das von dem betreffen-den Gegenstand reflektiert wird und auf den Phototransistor trifft. Um betrieben werden zu können bietet der Sensor das NXT Sensor Interface Pinout an. Dieses ist in sechs verschiedene Pins aufgeteilt. [Vgl. Bild]. Der erste Pin (weiß) übernimmt dabei die Funktion der Übertragung des analogen Outputs. Am zweiten (schwarz) und dritten (rot) Pin liegt die Erde an. Über den vierten Pin (grün) wird die Betriebsspannung angelegt. Die Steuerung des Modus lässt sich über den fünften Pin (gelb) des NXT Sensor Interface Pinouts steuern. Um den zweiten Modus zu wählen, wird an dem Pin eine Spannung von 5 V angelegt. Der sechste Pin ist beim Lichtsensor nicht belegt.^[1]

Inbetriebnahme des Sensors

Die Inbetriebnahme des Sensors ist über mehrere Varianten möglich. Die erste Variante ist die direkte Messwerterfassung über den EV3. Dabei wird zunächst ohne Computeranbindung eine Messwerterfassung gestartet. Auf dem Display wird der Graph mit den Messwerten in Echtzeit angezeigt. Zusätzlich können der Ist-Wert, die Dauer, Minimum und Maximum, sowie der Durchschnittswert angezeigt werden. Nach Beenden der Erfassung wird eine Messwertdatei auf dem Brick gespeichert, die über die Lego Mindstorms EV3 Education Software geöffnet werden kann. In der EV3-Software wird der Lichtsensor zu den Farbsensoren gezählt und kann über den Farbsensor-Block gesteuert werden. Trotz der unterschiedlichen Versionen ist die Nutzung des NXT-Sensors mit dem neueren EV3 möglich.

Da dieses Projekt in Matlab bzw. Simulink umgesetzt werden soll, muss eine Verbindung vom EV3 zu Matlab hergestellt werden. Für Matlab und Simulink ist jeweils ein Add-On verfügbar um den EV3 zu steuern. Nach Herstellen der Verbindung zwischen Matlab und dem Roboter können die verbundenen Sensoren ausgelesen werden. Die Kategorien sind analog zur EV3-Software. Der Lichtsensor wird allerdings nicht als „color“-Sensor, sondern als „NXT-Light“ angezeigt. Für das Auslesen des NXT-Lichtsensors ist keine eigene Funktion vorhanden. Auch ein Verbinden über die Funktion des Farbsensors, wie in der EV3-Software, ist nicht möglich. Für den NXT ist eine ähnliche Toolbox in Matlab verfügbar, die auch eine Funktion zum Aufrufen des NXT-Lichtsensors besitzt. Die Tool-box ist allerdings nicht mit dem EV3-Brick kompatibel, sodass keine Verbindung zum Brick hergestellt werden kann. Aus diesem Grund scheidet die Verwendung des EV3-Bricks im Nachhinein aus. Um trotzdem eine Umsetzung in Matlab bzw. Simulink zu ermöglichen, wird als Mikrocontroller nicht der EV3-Brick, sondern ein Arduino Uno genutzt. Da der Arduino nicht über einen Anschluss für das NXT Sensor Interface Pinout verfügt, musste das Verbindungskabel aufgetrennt werden. Um nicht das hochschuleigene Kabel zu nutzen, wurde ein eigenes gekauft, aufgetrennt und die einzelnen Adern mit Jumperkabeln, den Isolierungsfarben entsprechend, verbunden.

Rohsignale des Sensors

Abb. 7: Versuchsaufbau Kalibrierung

Die Rohsignale des Sensors liegen im Voltbereich zwischen 0 und 5 Volt. Nach der Verarbeitung sollen Werte zwischen 0 (dunkel) und 100 (hell) ausgegeben werden. Diese Werte sind einheitenlos.

Helligkeitsstufe	Ø EV3-Ergebnis	Ø Arduino-Ergebnis
0	0 LE	1.7780 LE
1	11.2 LE	11 LE
2	21.27 LE	20 LE
3	26.89 LE	26.009 LE
4	30.06 LE	29.572 LE
5	31.50 LE	31.653 LE
6	33.80 LE	33.492 LE

In der vorherigen Tabelle sind die Durchschnittswerte aus 1.000 Messungen des Lichtsensors aufgezeigt. Die Durchführung der Messungen zeigt, dass die Schaltung mit dem Arduino annähernd ähnliche Werte ergibt, wie durch das originale EV3-Mindstorms ermittelt werden.

Signalvorverarbeitung

Im Sensor selbst findet keine Vorverarbeitung der Daten statt. Das analoge Signal das von dem Phototransistor geliefert wird, wird erst im Arduino oder EV3 umgesetzt. Die Vorgehensweise ist im Kapitel Analog-Digital-Umsetzer beschrieben. Es werden also Messwerte und keine vorverarbeiteten Daten übergeben. Aus diesem Grund wird auch keine Sensorkennlinie eingesetzt.

Analog-Digital-Umsetzer

Der Analog-Digital-Umsetzer für die Signale des Lichtsensors sitzt im Co-Processor (Atmel AVR) des NXT-Brick. Die Funktionsweise wird im nachstehenden Kapitel beschrieben.

Umsetzung des analogen Signals

Der Phototransistor ändert seine Gleichspannung in Abhängigkeit zur Intensität des eingehenden Lichts. Die daraus folgenden analogen Daten werden danach über den ersten Pin des NXT SIP an den NXT- oder EV3-Brick weitergegeben. Dort wird das analoge Signal in ein digitales Signal umgesetzt. Für die Umsetzung wird ein 10Bit-ADU genutzt.

Funktionsweise des ADU

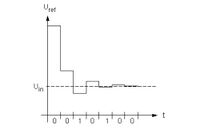
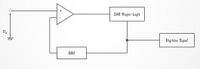
Verwendet wird der im Atmel AVR verbaute Analog-Digital-Wandler. Das zur Umsetzung genutzte Verfahren ist die sukzessive Approximation (SAP) und gehört zu den Stufen-wandlern. Zunächst wird ein Startimpuls, Start of Conversation (SOC) gesendet. Dieser setzt alle im (internen) Speicher befindlichen Register auf Null. Im weiteren Verlauf wer-den die analogen Eingänge mit Referenzspannungen verglichen. Diese Referenzspannung ändert sich mit jedem Schritt nach einer festen Reihenfolge. Es wird mit dem Most Significant Bit (MSB) gestartet und bis zum Least Significant Bit (LSB) fortgefahren. Für jeden Schritt wird die aktuelle Referenzspannung mit dem analogen Signal verglichen. Ist die Referenzspannung größer als das Signal, so wird das aktuelle Bit des Digitalwertes (im internen Speicher) auf Null gelassen. Wenn die Referenzspannung kleiner ist als das Signal, wird das aktuelle Bit auf Eins gesetzt. Wenn alle Schritte durchlaufen sind, wird das Signal End of Communication (EOC) gesendet. Die sukzessive Approximation beruht auf einer einfachen Komparatorschaltung (vgl. Abb. 9).

Stärken- und Schwächenanalyse

Die Stärken der sukzessiven Approximation liegen in der einfachen Umsetzung. Die Auflösung liegt im Regelfall zwischen zwölf und sechzehn Bit, aber auch eine Auflösung bei 10 Bit, wie in diesem Fall, ist möglich. Die SAP verwendet Abtastraten um die 100 kHz. Die einfache Umsetzung beeinträchtigt allerdings die Schnelligkeit des Verfahrens. In Bezug auf das Schnelligkeitskriterium ist die SAP im Nachteil zum Flash-ADU, der dafür aber in der Komplexität höher ist. Ein Flash-ADU hat eine kleinere Auflösung von 8 Bit und eine Abtastrate im GHz-Bereich. Eine weitere Alternative zum AD-Wandler mit sukzessiven Approximation ist ein Delta-Sigma-Wandler. Dieser wandelt das analoge Signal in 24 Bit bei einer Abtastrate von kleiner 100 kHz um. Nachteil des Delta-Sigma-Wandlers ist die Komplexität und die kleinere Abtastrate. Vorteil im Vergleich zur SAP ist die Fähigkeit zu einer hochauflösenden Erfassung der Messdaten. Ebenfalls ein hoch-aufgelöstes Ergebnis ist durch ein Dual-Slope-Wandler möglich. Dieser hat eine Auflösung von mehr als 20 Bit um eine Abtastrate im Hz-Bereich. Das Dual-Slope-Verfahren ist schneller als die sukzessive Approximation, aber im Vergleich komplexer umzusetzen. Zusammengefasst kann der AD-Wandler eher nicht für hochauflösende Messwerte verwendet werden und gehört zu den langsameren Umsetzern. Dafür ist die Komplexität sehr gering und der Umsetzungsaufwand klein. Die Ergebnisse durch die Anwendung dieses AD-Wandlers für den Lichtsensor sind in Bezug auf die Erwartungen angemessen.

Bussystem

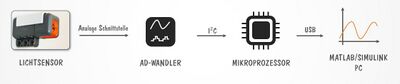
Bei der Verarbeitung der Daten des Lichtsensors werden verschiedene Bussysteme eingesetzt. Zunächst wird das Signal vom Sensor über eine analoge Schnittstelle an den EV3-Brick bzw. den Arduino geliefert. Dort wird das analoge Signal mittels eines Analog-Digital-Umsetzers in ein digitales Signal umgewandelt. Das digitale Signal wird im EV3-Brick über einen I²C-Bus an den Mikro-Prozessor weitergegeben. Für den Arduino gibt es keine eindeutigen Informationen für diese Übertragung. Die Datenübertragung vom Brick/ Arduino läuft über einen Universal Serial Bus.

Das inter-integrated circuit (I²C) Protokoll wurde von Philips in den 1980er Jahren entwickelt. Ende der 1990er wurde es zum Industriellen Standard. Eine Charakteristik des Protokolls ist z.B. die Initiierung der Datenübertragung. Diese beruht auf dem Master-Slave-Prinzip. Ein Mastergerät muss einen Slave dazu berechtigen die Datenübertragung zu starten. Auf einem I²C-Bus können die Daten in beiden Richtungen übertragen werden.^[4]

Der Universal Serial Bus (USB) wurde in den 1990er-Jahren im Auftrag des Universal Serial Bus Implementers Forum (USB-IF) entwickelt und standardsiert. Der USB ist einer der am häufigsten verwendeten Datenbusse überhaupt. Entwickelt wurde der USB um verschiedenste Daten, wie z.B. Audiodateien, Videos usw. zu übermitteln. Auf einem US-Bus können die Daten ebenfalls in beide Richtungen übertragen werden. I.d.R. wird der USB zum Verbinden eines Gerätes mit dem Computer verwendet. ^[5]

Digitale Signalverarbeitung

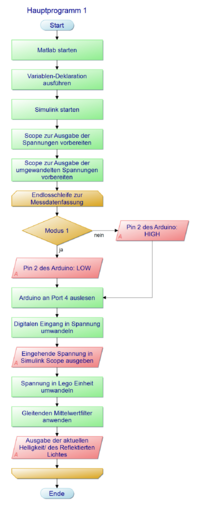
Für die digitale Signalverarbeitung sind mehrere Schritte notwendig. Zu Beginn muss Matlab gestartet werden. Daraufhin muss in Matlab eine Variablendeklaration stattfinden. Bei dieser Deklaration und anschließenden Initialisierung werden die maximal und minimal erhaltene Spannung festgelegt. Wenn diese Variablen gesetzt wurden, kann die Simulink-Datei geöffnet werden. Diese bereitet je einen Scope vor um die eingehende Spannungen und die Einheit in Lego-Einheiten zu zeigen. In einer Endlosschleife werden die eingehenden Signale an Pin A0 eingelesen. Vorher wird abgefragt ob Modus 1 (Umgebungslicht messen) oder Modus 2 (Helligkeit eines Gegenstandes messen) gewünscht ist. Je nach Wunsch wird das Hilfslicht an oder ausgeschaltet. Um die Spannung zu erhalten, wird der digitale Eingang wieder zurück gewandelt. Die eingehende Spannung wird im vorbereiteten Scope ausgegeben. Die Spannung wird nun in de Lego Einheiten umgewandelt und danach ausgegeben. Auf die eingehenden Werte wird dann noch ein rekursiver Mittelwertfilter angewendet und die Ergebnisse in einer Matlab-Figur ausgegeben.

Die Messdaten des Lichtsensors werden über den analogen Eingang des Arduino Uno eingelesen. Dabei wird das einfallende Licht in Abhängigkeit zur Helligkeit von einem Phototransistor in eine Spannung umgewandelt. Da das analoge Signal von einem 10 AD-Umsetzer umgesetzt wird und eine Spannung von 0V bis 5V ergibt sich folgende Auflösung:

    $\frac{5 V}{1023} = 4,88 mV$

Darstellung der Ergebnisse

Die folgende Tabelle zeigt die Messergebnisse bei der Helligkeitsstufe 6 (vgl Einfügen) in Abhängigkeit zu verschiedenen Farben und Farbstufen.

Farbton		1		2		3		4		5		Standardabw.		Messunsicherheit		Vertrauensintervall
		LE	V	LE	V	LE	V	LE	V	LE	V	LE	V	LE	V	LE	V
Rot	1	51	1.95	51	1.9672	51	1.9390	51	1.9617	51	1.9397	0	0.1273	0	0.0389	51±0.000	1.5091±0.0389
	2	55	2.0674	55	2.0434	55	2.0582	55	2.0511	55	2.0663	0	0.1019	0	0.0311	55±0.000	2.0573±0.0311
	3	55	2.0746	55	2.0539	55	2.0678	55	2.0486	55	2.0678	0	0.1084	0	0.0331	55±0.000	2.0625±0.0331
Gelb	1	40	1.4922	41	1.5504	41	1.5342	41	1.5511	41	1.5359	0.4472	0.2400	0.1365	0.07326	40.8+0.1365	1.5328±0.07326
	2	53	1.9802	53	1.9855	52	1.9423	53	1.9975	53	1.9841	0.4472	0.2093	0.1365	0.0639	52.8±0.1365	1.9779±0.0639
	3	57	2.1350	57	2.1430	57	2.1346	57	2.1436	57	2.1253	0	0.0748	0	0.0228	57±0.000	2.1363±0.0228
Grün	1	33	1.2514	33	1.2365	33	1.2487	33	1.2495	33	1.2615	0	0.0891	0	0.0272	33±0.000	1.2495±0.0272
	2	43	1.6126	43	1.6189	43	1.6253	43	1.6017	43	1.6151	0	0.0871	0	0.0266	43±0.000	1.6147±0.0266
	3	55	2.0798	54	2.0327	55	2.0604	55	2.0704	55	2.0783	0.4472	0.1928	0.1365	0.0589	54.8±0.1365	2.0643±0.0589
Blau	1	31	1.1715	31	1.1603	31	1.1667	31	1.1576	31	1.1679	0	0.0570	0	0.0174	31±0.000	1.1648±0.0174
	2	36	1.3448	36	1.3602	36	1.3638	36	1.3390	36	1.3592	0	0.1083	0	0.0330	36±0.000	1.3534±0.0330
	3	51	1.9272	51	1.9004	51	1.9099	51	1.9188	51	1.9133	0	0.0999	0	0.0305	51±0.000	1.9139±0.0305

Für die folgenden Berechnungen ist zunächst die Formel der Standardabweichung (2) zu kennen.

 $s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})$  (2)

Außerdem wird die Varianz (3) in der unten stehenden Tabelle genutzt.

 $s = \sqrt{s^2} = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2}$  (3)

Um die Messunsicherheit(4) mit der StudenT-Verteilung zu berechnen wird folgende Formel verwendet:

 $\Delta d = t(n)\cdot \frac{s}{\sqrt{n}}$  (4)

Das Vertrauensintervall umfasst den Bereich

 $Vertrauensintervall = \bar{x} \pm s^2$  (5)

Ein Hilfsmittel zur Bestimmung der Qualität eines Sensors ist das Heranziehen der Messunsicherheit. Diese lässt sich mit Hilfe der StudenT-Verteilung ermitteln. Zunächst wird die Standardabweichung der Messwerte gebildet. Da dieser Sensor eher im Bereich von kleinen Experimenten genutzt wird, etwa dem Erkennen von dunklen Linien bei der Überfahrt mit einem Legoroboter, werden für die Bestimmung der Messunsicherheit nur die ersten fünf Messungen betrachtet. Die Standardabweichung wird dann mit der Standardabweichung in 10.000 Messungen verglichen. Da dieser Sensor bereits älter ist und aus einem Experimentierbaukasten stammt, wird der Grad des Vertrauens nicht auf 95%, wie von der Industriellen Messtechnik erwartet, bestimmt. Stattdessen wird von einem Vertrauensintervall im Bereich von Physik und Vermessungswesen ausgegangen. Der Grad des Vertrauens liegt dann bei 68.26%. Die Analyse bezieht sich nicht nur auf die Rohwerte, sondern auch auf die zum Schluss an den Nutzer weitergegebenen Lego-Einheiten. Die Rohwerte werden deshalb noch zusätzlich betrachtet, da sie eine genauere Auskunft Abweichungen geben. In der unteren Tabelle erkennt man die Standardabweichung bei 10.000 Messungen. Je mehr Messungen getätigt werden, desto mehr kann der Standardabweichung vertraut werden. Anders als vermutet ist die Standardabweichung viel geringer, die Qualität des Sensors also etwas höher als geschätzt.

Farbton	Ø 10.000 Werte		Standardabweichung		Varianz
	LE	V	LE	V	LE	V
Rot 1	52.0144	1.9507	0.11914	0.0117	0.0142	0.0001
Rot 2	54.9995	2.0161	0.0224	0.0107	0.0005	0.0001
Rot 3	54.9737	2.0607	0.1600	0.0122	0.0256	0.0002
Gelb 1	40.8021	1.5343	0.3984	0.0183	0.1588	0.0003
Gelb 2	52.79	1.9794	0.4073	0.0185	0.1659	0.0003
Gelb 3	57	2.1359	0	0.0107	0	0.0001
Grün 1	32.9999	1.2444	0.01	0.0107	0.0001	0.0001
Grün 2	42.9999	1.6158	0.01	0.0107	0.0001	0.0001
Grün 3	54.9824	2.0609	0.1315	0.0117	0.0172	0.0001
Blau 1	31.2059	1.2045	0.4043	0.0184	0.1635	0.0003
Blau 2	36.0233	1.3567	0.1509	0.0121	0.0228	0.0001
Blau 3	50.9858	1.9126	0.1183	0.0116	0.014	0.0001

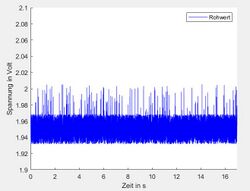
Generell lässt sich aber nicht erkennen, dass die Standardabweichung bzw. Messunsicherheit größer wird, je dunkler das gemessene Objekt ist. Ein helles Objekt kann deshalb nicht besser bestimmt werden, als ein dunkles. In Abb. 14 lassen sich die Messwerte bei den Farben Rot 1 bis Rot 3 erkennen. Zusätzlich ist der Gleitende Mittelwert-Filter dargestellt. In Abb. 15 sind die Rohwerte des Sensors in Volt gezeigt.

YouTube-Video

Zu dieser Ausarbeitung ist auch ein zwei Youtube-Videos erstellt worden. Das erste YouTube-Video zeigt nur die Echtzeit-Simulation. Das zweite YouTube-Video ist ausführlicher (Dauer ca.5 Minuten) und zeigt die grundlegenden Ergebnisse des Projektes, sowie eine kurze Echtzeit-Datenerfassung des Sensors in Matlab.

Herausgeber: Eileen Hinners
Hochschule: Hochschule Hamm-Lippstadt
Studiengang: Business and Systems Engineering, 1. Fachsemester
Projektkurs: Signalverarbeitende Systeme
Ziel: Sensordaten in Echtzeit auslesen und in Matlab verwenden
Ergebnis: Der Sensor konnte mit einem Arduino Uno ausgelesen und in Matlab/Simulink verwendet werden.
Beschreibung: Dieses Video zeigt die grundlegenden Ergebnisse des Projektes, sowie eine Echtzeit-Datenerfassung des Sensors in Matlab
Betreuer: Prof. Dr. Ulrich Schneider

SVN Projektordner

In dem nachstehenden Ordner im SVN sind alle Unterlagen zum Projekt abgelegt.

Literaturverzeichnis

↑ Datenblatt NXT-Lichtsensor
↑ vias.org
↑ Mitschrift aus Vorlesung
↑ Han-Way Huang. HCS12/9S12 An Introduction to Software and Hardware Interfacing. 2. Auflage. New York: Delmar. 2009
↑ S. McDowell, M. D. Seyer. USB explained. Complete coverage of today's hottest new connectivity standard. 2. Auflage. New Jersey: Pearson Education. 1999

→ zurück zum Hauptartikel: SigSys SoSe2018

[1] Datenblatt NXT-Lichtsensor

[2] vias.org

[3] Mitschrift aus Vorlesung

[4] Han-Way Huang. HCS12/9S12 An Introduction to Software and Hardware Interfacing. 2. Auflage. New York: Delmar. 2009

[5] S. McDowell, M. D. Seyer. USB explained. Complete coverage of today's hottest new connectivity standard. 2. Auflage. New Jersey: Pearson Education. 1999

[1]

[2]

[3]

[4]

[5]