Entwicklung eines geregelten Wasserstandssystems für die Hochschullehre

Autor:	Denim Hilz
Erstprüfer:	Prof. Göbel
Zweitprüfer:	Prof. Tikhomirov
Wissenschaftliche Unterstützung:	Marc Ebmeyer

Abbildung 1: Wasserstandssystem

Einleitung

Dieser Wiki-Artikel stellt die Masterarbeit

Modellierung, Simulation und Echtzeit-Implementierung eines geregelten Wasserstandssystems mit MATLAB/Simulink und Mikrocontrollertechnik
für praxisorientierte Hochschuldemonstrationen im Rahmen der regelungstechnischen Lehre

vor. Dabei werden Planung, Entwicklung und Umsetzung aufgezeigt sowie die erzielten Ergebnisse dokumentiert.

Die Regelungstechnik ist eine Kernkompetenz für Ingenieurinnen und Ingenieure, da sie Steuerung und Regelung technischer Prozesse vermittelt. Um die oft abstrakte Theorie greifbarer zu machen, eignen sich praxisnahe Werkzeuge wie MATLAB/Simulink und Mikrocontrollertechnik.

Ziel der Masterarbeit war die Entwicklung eines didaktisch einsetzbaren Wasserstandssystems für die regelungstechnische Lehre an der Hochschule Hamm-Lippstadt (HSHL), um Theorie und Praxis zu verknüpfen.

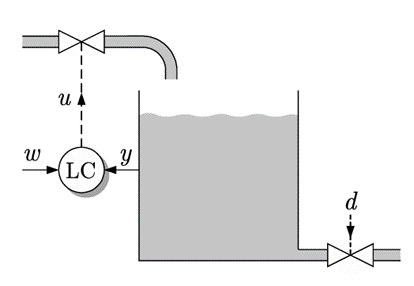
Die entwickelten Regelungskonzepte basieren auf einem grundlegenden Schema der Füllstandsregelung (Level Control, LC), wie in der folgenden Abbildung dargestellt. Ziel ist es, den Wasserstand eines Behälters auf eine Sollhöhe 𝑤 (z. B. 1 m) zu bringen und dort zu halten. Die Stellgröße 𝑢 beeinflusst den Zufluss, ein Sensor misst die Ist-Höhe 𝑦. Externe Einflüsse wie Wasserentnahme wirken als Störung 𝑑 und müssen ausgeglichen werden.

Solche Systeme sind nicht nur für Lehrzwecke relevant, sondern auch in der Industrie – etwa zur Vermeidung von Überlauf, Trockenlauf oder unerwünschten Schwankungen. Die Planung und Entwicklung orientiert sich an diesem Grundschema.

Abbildung 2: Beispielhafter Aufbau eines Wasserstandssystems

Die Masterarbeit umfasst:

• die Modellierung des Tanksystems,
• die Simulation des physikalischen Verhaltens und der Reglerauslegung mit MATLAB/Simulink,
• sowie die Echtzeit-Implementierung des Reglers auf einem Mikrocontroller.

Durch die Integration von MATLAB/Simulink und Mikrocontrollertechnik wird eine enge Verbindung zu den im Studium vermittelten Lehrinhalten geschaffen.

Theoretische Grundlagen

In diesem Abschnitt wird das grundlegende mathematische Modell und die Übertragungsfunktion des Wasserstandssystems dargestellt. Die Herleitung der Übertragungsfunktion des zylindrischen Wassertanks sowie die Auswahl des geeigneten Reglers bilden die Basis für die Simulation und Regelung des Systems. Das Vorgehen orientiert sich an der Formelsammlung aus der Lehrveranstaltung Mess- und Regelungstechnik.

Übertragungsfunktion des Wassertanks

Für die Regler-Auswahl und die Simulation ist es wichtig, das Verhältnis vom Ausgangssignal zum Eingangssignal des Systems, also die Übertragungsfunktion, zu kennen . Der für die Umsetzung gewählte Wassertank besitzt eine zylindrische Form. Der Wasserstand im Tank wird direkt vom Volumenstrom der Pumpe beeinflusst. Die Übertragungsfunktion lässt sich somit aus der geometrischen Berechnung des Volumens des Wassertanks herleiten.

Das Vorgehen zur Bestimmung der Übertragungsfunktion orientiert sich an der Vorlesung Systemtheorie, siehe .

Die Volumenberechnung erfolgt gemäß nach folgender Formel:

$V=A\cdot h$

Mit:

• \(V\): Volumen des Wassers im Tank in \(\mathrm{m}^3\)
• \(A\): Querschnittsfläche des Tanks in \(\mathrm{m}^2\)
• \(h(t)\): Wasserstand im Tank in \(\mathrm{m}\)

Da sich der Wasserstand durch den Zu- bzw. Abfluss verändert, ergibt sich durch Ableitung der Formel nach der Zeit folgende Differentialgleichung (DGL):

$\frac{dV}{dt}=A\cdot \frac{dh}{dt}$

Mit:

• $\dot{V}$: zeitliche Änderung des Volumens in \(\mathrm{m}^3\,\mathrm{s}^{-1}\)
• $\dot{h}$: zeitliche Änderung des Wasserstands in \(\mathrm{m}\,\mathrm{s}^{-1}\)

Mittels Laplace-Transformation ergibt sich die Gleichung:

$\dot{V}(s)=A\cdot s\cdot h(s)$

Da $\dot{V}$ (andere Bezeichnung für den Volumenstrom \(Q\)) bereits eine Flussgröße ist, bleibt $\dot{V}$ im Laplace-Bereich stehen und wird nicht mit \(s\) multipliziert.

Die Übertragungsfunktion kann aus obiger Gleichung hergeleitet werden und ergibt sich aus dem Verhältnis von Ausgang zu Eingang:

$G(s)=\frac{h(s)}{\dot{V}(s)}=\frac{1}{A\cdot s}$.

Regler-Auswahl

Die Regelung mittels PID-Regler findet in der Praxis sowie in der regelungstechnischen Lehre an der HSHL häufig Anwendung. Aufgrund dieser Relevanz wurde für das vorliegende Projekt eine Regelung mit dem PID-Regler ausgewählt.

Im Folgenden ist für die PID-Anteile die Berechnung des stationären Endwertes \(x_{stat}\) der Führungsübertragungsfunktion \(G_W\) und der Störübertragungsfunktion \(G_Z\) bei einem Einheitssprung aufgezeigt.

Ziel der Untersuchung ist es herauszufinden, bei welcher Kombination der Regelanteile die Regelgröße im stationären Zustand exakt der Führungsgröße entspricht und äußere Störungen kompensiert werden. Das bedeutet:

• Für \(G_W\) sollte im Idealfall \(x_{stat} = 1\) gelten
• Für \(G_Z\) sollte im Idealfall \(x_{stat} = 0\) gelten

Die Berechnungen für P, PI, PD und PID zeigen, dass nur PI und PID bei einem Einheitssprung die beiden Bedingungen erfüllen.

Die Herleitung der Führungs- und Störübertragungsfunktion für den PI-Regler ist an dieser Stelle aufgezeigt und orientiert sich an dem Vorgehen aus der Lehrveranstaltung Regelungstechnische Systeme, siehe .

Führungsübertragungsfunktion

$G_W=x_w=\frac{G_R\cdot G_S}{1+G_M\cdot G_R\cdot G_S}$

wobei

• \(G_M = 1\)
• \(G_S = \frac{1}{A \cdot s}\)
• \(G_R = K_P + \frac{K_I}{s}\)

Es gilt:

$G_{WPI}=\frac{(K_P+\frac{K_I}{s})\cdot \frac{1}{A\cdot s}}{1+1\cdot (K_P+\frac{K_I}{s})\cdot \frac{1}{A\cdot s}}=\frac{K_P\cdot \frac{1}{A\cdot s}+K_I\cdot \frac{1}{A\cdot s^2}}{1+K_P\cdot \frac{1}{A\cdot s}+K_I\cdot \frac{1}{A\cdot s^2}}\cdot \frac{A\cdot s^2}{A\cdot s^2}=\frac{K_{P}s+K_I}{A{s}^2+K_{P}s+K_I}$

Der stationäre Endwert ergibt sich zu:

$x_{stat}=\underset{t\to \mathrm{\infty }}{\lim }x(t)=\underset{s\to 0}{\lim }{G}_{WPI}(s)=\frac{K_P\cdot 0+K_I}{A\cdot 0^2+K_P\cdot 0+K_I}=1$

Zur Vereinfachung der Regler-Auslegung wurde sich im weiteren Verlauf für den PI-Regler entschieden. Die PI-Regeleinrichtung ermöglicht die Erreichung des vorgegebenen Sollwertes bei gleichzeitiger Kompensationsfähigkeit von auftretenden Störungen .

Störübertragungsfunktion

$G_Z=x_z=\frac{G_S}{1+G_M\cdot G_R\cdot G_S}$

wobei die gleichen Werte für \(G_M, G_S, G_R\) gelten wie oben.

$G_{ZPI}=\frac{\frac{1}{A\cdot s}}{1+1\cdot (K_P+\frac{K_I}{s})\cdot \frac{1}{A\cdot s}}=\frac{\frac{1}{A\cdot s}}{1+K_P\cdot \frac{1}{A\cdot s}+K_I\cdot \frac{1}{A\cdot s^2}}\cdot \frac{A\cdot s^2}{A\cdot s^2}=\frac{s}{A{s}^2+K_{P}s+K_I}$

Der stationäre Endwert ergibt sich zu:

$x_{stat}=\underset{t\to \mathrm{\infty }}{\lim }x(t)=\underset{s\to 0}{\lim }{G}_{ZPI}(s)=\frac{0}{A\cdot 0^2+K_P\cdot 0+K_I}=0$

Systemverhalten bei geschlossenem Regelkreis

Das Systemverhalten bei geschlossenem Regelkreis kann anhand der Führungsübertragungsfunktion des P-Reglers aufgezeigt werden. Der P-Regler verstärkt lediglich und fügt keine eigene Dynamik hinzu . Die Funktion ergibt sich zu:

$G_{WP}=\frac{K_P\cdot \frac{1}{A\cdot s}}{1+1\cdot K_P\cdot \frac{1}{A\cdot s}}\cdot \frac{A\cdot s}{A\cdot s}=\frac{K_P}{A\cdot s+K_P}$

Es zeigt sich, dass das Verhalten dem eines PT1-Systems gleicht mit

$K_P\approx K_P;T\cdot s\approx A\cdot s;1\approx K_P$.

Systementwurf und Umsetzung

Dieses Kapitel beschreibt Modellierung, Simulation und Umsetzung des geregelten Wasserstandssystems basierend auf den theoretischen Grundlagen.

Regelkreis

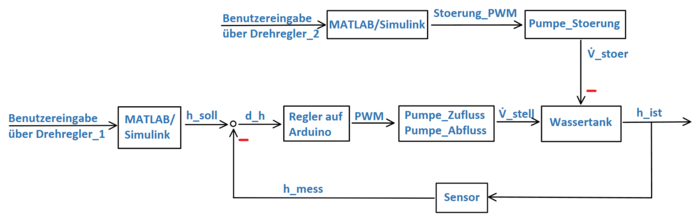
Zur Veranschaulichung dient der schematische Aufbau eines geschlossenen Regelkreises (Abbildung 3). Ziel ist, den Wasserstand eines Primärtanks auf eine vorgegebene Sollhöhe 𝒉ₛₒₗₗ einzustellen und bei Störungen konstant zu halten.

Der Regelkreis zeigt folgende Funktionen:

• Der Benutzer gibt über ein Potentiometer die Sollhöhe 𝒉ₛₒₗₗ (Führungsgröße) vor.
• Die Differenz zur gemessenen Ist-Höhe 𝒉ₘₑₛₛ (Messgröße) ergibt den Regelfehler Δ𝒉, der vom Mikrocontroller (Arduino) ausgewertet wird.
• Ein PI-Regler berechnet ein Ausgangssignal zur Ansteuerung von zwei Pumpen für geregelten Zu- und Abfluss.
• Die Ansteuerung erfolgt über PWM-Signale, die über H-Brücken an die Pumpen weitergegeben werden (Stellgröße 1).
• Daraus entsteht ein resultierender Volumenstrom 𝑽ₛₜₑₗₗ (Stellgröße 2), der den Wasserstand verändert.
• Eine einstellbare Störung 𝑽ₛₜₒₑᵣ, über ein zweites Potentiometer gesteuert, ermöglicht den Abfluss.

Abbildung 3: Schematischer Regelkreis des Wasserstandssystems i.A.a.

Konzeptskizze

Zur Auswahl und Bewertung möglicher Systemkomponenten wurde ein morphologischer Kasten verwendet (siehe Anhang Masterarbeit). Verschiedene Optionen wurden nach Kriterien wie Kompatibilität, Kosten, Verfügbarkeit und Benutzerfreundlichkeit bewertet.

Ausgewählte Kriterien waren Kompatibilität (Arduino/MATLAB-Anbindung), Verfügbarkeit, Kosten und Anwenderfreundlichkeit (z. B. für Besucher des MINT-Erlebnistags).

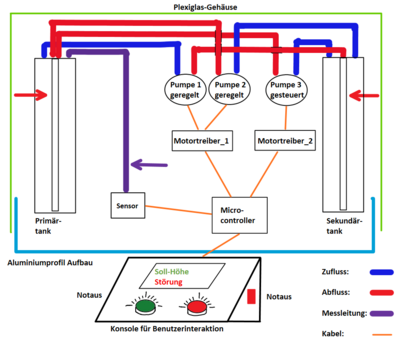
Abbildung 4 zeigt die Konzeptskizze. Der Aufbau:

• Zwei Glaszylinder aus Borosilikatglas als Primär- und Sekundärtank, verbunden durch Silikonschläuche,
• Pumpe 1: geregelter Zufluss (blau),
• Pumpe 2: geregelter Abfluss (rot),
• Pumpe 3: manuelle Störung (orange),
• Drucksensor zur Wasserstandsmessung,
• Zwei Drehpotentiometer zur Eingabe von Sollwert und Störung (grün/rot),
• LCD-Anzeige zur Darstellung von Sollwert, Istwert und Störung,
• Arduino-Controller mit H-Brücken zur Pumpensteuerung,
• Montage auf Aluminiumrahmen mit Plexiglas-Gehäuse.

Abbildung 4: Konzeptskizze des Wasserstandssystems

Der Wasserzufluss erfolgt von oben, der Abfluss über den Tankboden. Die Konstruktion ermöglicht gute Sichtbarkeit und leichte Zugänglichkeit – besonders vorteilhaft im Hochschulkontext.

Das System ist in folgende Komponenten unterteilt:

1. Wassertanksystem
2. Benutzereingabe_Hoehe
3. Benutzereingabe_Stoerung
4. Pumpe_Regelung
5. Pumpe_Stoerung
6. Regelung
7. Sensor
8. I2C_LCD_20x4.

Simulation

Die Simulation erfolgte in MATLAB/Simulink und diente der Reglerauslegung, dem Systemverständnis und der Bewertung des dynamischen Verhaltens bei Sollwertänderungen und Störungen.

Anti-Windup

Da die PWM auf 255 begrenzt ist und die Regelung einen I-Anteil enthält, wurde eine Anti-Windup-Maßnahme implementiert. Sie beschränkt den Integratorausgang auf −255 bis +255, um eine unkontrollierte Aufintegrierung zu verhindern.

Zur Veranschaulichung wurde eine 120 s lange Simulation ohne und mit Anti-Windup durchgeführt.

Abbildung 5 vergleicht den kumulierten Regelfehler beider Simulationen und zeigt, dass der Fehler mit Anti-Windup um den Faktor fünf reduziert wurde.

Abbildung 5: Simulation - Auswirkung von Anti-Windup auf den Regelfehler

Auswahl geeigneter Reglerparameter

Für die finale Reglerauslegung wurden mehrere Kombinationen von Kₚ und Kᵢ mit aktiviertem Anti-Windup getestet. Abbildung 6 zeigt Sollhöhe, Ist-Höhe und Regelfehler.

Ergebnisse:

• Kₚ = 100, Kᵢ = 100: langsame Regelung, starkes Überschwingen, unzureichende Störkompensation
• Kₚ = 10000, Kᵢ = 10000: schnelle Regelung, aber starkes Nachschwingen
• Kₚ = 10000, Kᵢ = 5000: bestes Führungs- und Störverhalten

Abbildung 6: Simulation – Reglerauslegung

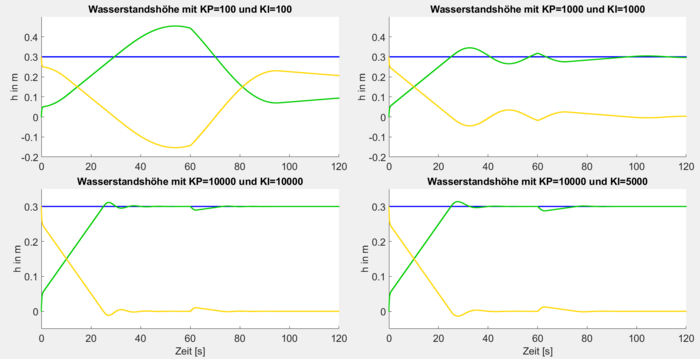
Trotz leicht höherem Regelfehler zeigt Kₚ = 10000, Kᵢ = 5000 geringeres Schwingen und bessere Stabilität. Da reale Einflüsse (Pumpen-/Sensordynamik) weitere Dynamik hinzufügen, wurden diese Parameter für die Echtzeitumsetzung gewählt.

Zusammenfassung

Die Simulationen zeigen deutlich:

• Der Anti-Windup-Maßnahme ist essenziell für die Systemanforderungen.
• Die finale Auswahl Kₚ = 10000 und Kᵢ = 5000 erfüllt Anforderungen an Geschwindigkeit, Genauigkeit und Störunterdrückung.
• Die Modellierung ermöglichte fundierte Entscheidungen vor der Hardwareimplementierung.

Systemumsetzung

Das System wurde in einzelne Komponenten unterteilt, um die Umsetzung sowohl hardware- als auch softwareseitig strukturiert durchzuführen. In diesem Kapitel werden die wichtigsten Funktionen und Eigenschaften für jede Komponente vorgestellt.

Wassertanksystem

Die Umsetzung des Wassertanksystems ist ausschließlich hardwareseitig erfolgt. Die wichtigsten Punkte sind:

• Der Wasserstand im Primärtank wird kontinuierlich überwacht und geregelt.
• Die optimale Menge an destilliertem Wasser beträgt 1,6 l. Damit ist ein Über- oder Trockenlaufen der Glaszylinder nicht möglich.
• Die maximale Füllhöhe in einem der Tanks liegt bei maximal ca. 0,35 m, was ein leichtes Überschwingen über die maximale Sollhöhe ermöglicht.

Benutzereingabe_Hoehe

Diese Komponente erlaubt dem Benutzer die Vorgabe einer Sollhöhe des Wasserstands über ein Potentiometer. Die Softwareumsetzung ist in der folgenden Abbildung aufgezeigt.

• Die Werte werden über A1 des Arduinos in Simulink eingelesen.
• Ein 100 nF Kondensator stabilisiert die analogen Werte.
• Eine Mittelwertfilterung über fünf Messwerte wird mit dem MATLAB-Function-Block Benutzereingabe_Hoehe_Mittelwert_Berechnung umgesetzt.
• Die gefilterten Digitalwerte werden in einem 1-D Lookup Table in Meter umgerechnet.
• Der Digitalwertbereich ist wie folgt definiert:

 Digitalwert ≤ 5 entspricht 0,05 m
 Digitalwert ≥ 1018 entspricht 0,30 m

Abbildung 7: Softwareumsetzung der Komponente Benutzereingabe_Hoehe

Benutzereingabe_Stoerung

Über ein zweites Potentiometer kann der Benutzer eine Störung in Prozent vorgeben. Die Softwareumsetzung ist in der folgenden Abbildung aufgezeigt.

• Auch hier erfolgt die Einlesung über einen Arduino-Analogkanal in Simulink.
• Der Aufbau ist identisch zur Benutzereingabe_Hoehe, inklusive 100 nF Kondensator und Mittelwertfilterung über fünf Werte.
• Die Umrechnung von Digitalwert auf Störgröße in Prozent erfolgt in einem 1-D Lookup Table.
• Die Ausgabe wird durch einen Round-Block auf ganze Prozent gerundet.
• Der Digitalwertbereich ist wie folgt festgelegt:

 Digitalwert ≤ 5 entspricht 0 % Störung
 Digitalwert ≥ 1018 entspricht 100 % Störung

Abbildung 8: Softwareumsetzung der Komponente Benutzereingabe_Stoerung

Pumpe_Regelung

Die Komponente Pumpe_Regelung besteht aus einer Zufluss- und einer Abflusspumpe, die über die Software mit einer PWM angesteuert werden. Die Softwareumsetzung ist in der folgenden Abbildung aufgezeigt.

• Das Regelsignal Regelung_PWM wird zunächst über einen Round-Block gerundet und anschließend durch einen Abs-Block geleitet, um eine positive, ganzzahlige PWM zu erzeugen.
• Da die Pumpen erst ab einem PWM-Wert von 71 anlaufen, wird dieser Wert über den Lookup Table Regelung_PWM-Offset als Offset hinterlegt:

 0 % ≙ 0 PWM
 1 % ≙ 71 PWM
 100 % ≙ 255 PWM

• Das Offset-Signal wird über zwei Switch-Blöcke weitergeleitet:

 PR_PWM_>_0 steuert die Zuflusspumpe bei positiver PWM,
 PR_PWM_<=_0 steuert die Abflusspumpe bei negativer PWM.

• Das Vergleichssignal PWM_Vergleich entscheidet über die Umschaltung:

 Wenn PWM > 0: PWM_Vergleich = 0
 Wenn PWM ≤ 0: PWM_Vergleich = 1
 Steuerung erfolgt über PAR_PR_Vergleich_Switch = 0

• Zur Entscheidungsfindung wird das Signal Regelung_PWM_round vor dem Abs-Block abgezweigt und dem Vergleichsoperator PR_Vergleichsoperator zugeführt.

 Bei positiver PWM: Ansteuerung von Regelung_PWM_Zufluss (Pins 3 und 4)
 Bei negativer PWM: Ansteuerung von Regelung_PWM_Abfluss (Pins 6 und 7)

• Da der Arduino PWM-Block nur ganzzahlige Werte verarbeiten kann, werden alle PWM-Signale in 16-Bit-Ganzzahlen umgewandelt.

Abbildung 9: Softwareumsetzung der Komponente Pumpe_Regelung

Pumpe_Stoerung

Die Komponente Pumpe_Stoerung ermöglicht die gezielte Aktivierung der Membranpumpe zur Erzeugung einer Störung im Wasserstandssystem. Die Softwareumsetzung ist in der folgenden Abbildung aufgezeigt.

• In Simulink wird das Signal BES_Stoerung_Prozent über einen 1-D Lookup Table (Stoerung_Prozent-PWM_Offset) einem PWM-Wert zugeordnet. Es gilt:

 0 % ≙ 0 PWM
 1 % ≙ 71 PWM
 100 % ≙ 255 PWM

• Der Offset von 71 sorgt dafür, dass die Pumpe bereits bei geringen Störprozentwerten anläuft.
• Das berechnete Signal Stoerung_PWM wird in eine 16-Bit-Ganzzahl umgewandelt.
• Anschließend erfolgt die Ausgabe über PS_Pumpe_Stoerung_PWM und PS_Pumpe_Stoerung_Drehrichtung an die PWM-Pins 8 und 9 des Arduino.

Abbildung 10: Softwareumsetzung der Komponente Pumpe_Stoerung

Regelung

Die Komponente Regelung bildet das Herzstück des Systems. Sie verarbeitet den Regelfehler und gibt ein PWM-Signal zur Ansteuerung der Zulaufpumpe aus. Die Softwareumsetzung ist in der folgenden Abbildung aufgezeigt.

• In Simulink wird kontinuierlich die Differenz d_h zwischen h_soll und h_mess berechnet.
• Der Fehler wird in einen P-Anteil und einen I-Anteil aufgeteilt.
• Die Verstärkungen erfolgen über die Parameter PAR_RG_KP (P-Anteil) und PAR_RG_KI (I-Anteil).
• Der I-Anteil wird über einen Integrator mit Anti-Windup-Grenzen (−255 bis 255) summiert.
• Beide Anteile werden anschließend im Sum-Block addiert.
• Das Ergebnis wird im Saturation-Block von −255 bis 255 begrenzt, um die Stellgröße Reglung_PWM zu erzeugen.
• Dieses Signal wird direkt an die Komponente Pumpe_Regelung übergeben.

Abbildung 11: Softwareumsetzung der Komponente Regelung

Sensor

Diese Komponente misst den aktuellen Wasserstand über den Differenzdrucksensor MPX5010DP. Um die Qualität der Messwerte zu erhöhen, wurden sowohl Hardware- als auch Softwarefilterungen umgesetzt. Die Softwareumsetzung ist in der folgenden Abbildung aufgezeigt.

• Die Versorgungsspannung des Sensors ist über ein Power Supply Module (PSM) vom Arduino entkoppelt, um die Spannung zu stabilisieren.
• Die analoge Ausgangsspannung wird über A0 eingelesen.
• Eine zusätzliche Ausgangsfilterung gemäß AN1646 wurde zur Dämpfung des Sensorrauschens auf einer Lochrasterplatine umgesetzt.
• Die Software verwendet einen PT1-Filter nach Prof. Dr.-Ing. Mirek Göbel zur Signalglättung.
• Die Filterausgabe wird gerundet, um zusätzliche Schwankungen zu reduzieren.
• Die Zuordnung des Digitalwerts zur Höhe erfolgt mit einem 1D-Lookup Table.
• Die Kalibrierung ergab ein Bestimmtheitsmaß R² = 0,9994 und eine Messgenauigkeit von ±5 mm.

Abbildung 12: Softwareumsetzung der Komponente Sensor

I2C_LCD_20x4

Diese Komponente stellt die aktuellen Mess- und Sollwerte des Wasserstands auf einem LCD-Display dar. Die Anzeige erfolgt in Millimetern zur besseren Lesbarkeit. Die Softwareumsetzung ist in der folgenden Abbildung aufgezeigt.

• Die Werte für h_soll und h_mess werden mit dem Faktor 1000 multipliziert, um von Metern in Millimeter umzuwandeln (PAR_LCD_Millimeter).
• Die Signale werden über den Data-Type Conversion Block in int16 konvertiert, da Werte über 128 korrekt dargestellt werden sollen.
• Die Kommunikation mit dem Display erfolgt über die I2C-Schnittstelle.
• Verwendet wird die LiquidCrystal_I2C Library von Frank de Brabander.
• Die Erstellung des IO-Device-Blocks erfolgte anhand des MATLAB-Tutorials „Get Started with IO Device Builder“.

Abbildung 13: Softwareumsetzung der Komponente I2C_LCD_20x4

Systemtest und Ergebnisse

Dieses Kapitel dokumentiert die Tests des realen Systems sowie die wichtigsten Ergebnisse.

Systemverhalten bei Sollwertansteuerung und Störungseinfluss

Die Tests wurden mit den Reglerparametern 𝐾𝑃 = 10000, 𝐾𝐼 = 5000 bei einer Frequenz von 1 Hz durchgeführt. Im ersten Versuch (Abbildung 14) wurde eine Sollhöhe von 0,30 m bei Sekunde 15 eingestellt. Die Ist-Höhe folgte verzögert und schwang zunächst über, bevor sie sich nach etwa 70 s im Toleranzbereich von ±5 mm einpendelte.

Trotz implementierter Anti-Windup-Maßnahme musste sich der I-Anteil des Reglers abbauen, wodurch eine träge Reaktion entstand. Die Filterung reduzierte zwar das Sensorsignalrauschen, verursachte jedoch ein Delay von bis zu 2 s. Die PWM-Werte zeigen den erwarteten Ablauf und steuern je nach Bedarf die passende Pumpe für den Zu- oder Abfluss an

Abbildung 14: 1. Systemtest mit Anfahren der Soll-Höhe

Im zweiten Versuch (Abbildung 15) wurde bei Sekunde 70 eine Störung mit 90 % Intensität zugeschaltet. Die Folge war ein kurzzeitiger Abfall der Wasserhöhe, welcher ab Sekunde 81 durch das System kontrolliert kompensiert wurde. Die vollständige Störkompensation wurde nach etwa 70 s erreicht. Die Störkompensation mit PI-Regler ist somit möglich.

Die Reaktion auf die Störung zeigte jedoch auch eine Sensorverzögerung infolge Messkette und Filterung, sowie eine erkennbare Asymmetrie der PWM-Werte bei Zufluss- und Störungspumpe, was auf unterschiedliche reale Fördermengen hindeutet.

Abbildung 15: 2. Systemtest mit Störung

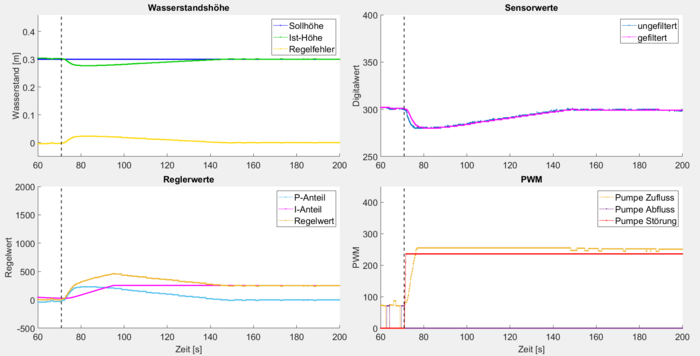
Ergebnisse

Das System erreicht die gewünschte Sollhöhe zuverlässig, zeigt jedoch Überschwinger und reagiert verzögert, verursacht durch Filterung, Messkettenträgheit und physikalische Totzeiten. Die implementierte Anti-Windup-Funktion arbeitet wie gewünscht und verhindert eine unkontrollierte Aufintegration des Reglers.

Die Störkompensation mit 90 % Intensität ist grundsätzlich möglich, benötigte im Test jedoch rund 70 s. Dabei zeigte sich, dass der P-Anteil allein nicht ausreicht, um die Abweichung auszugleichen – erst der I-Anteil sorgt für eine vollständige Kompensation. Die PWM-Steuerung der Pumpen reagiert verzögert, was vermutlich auf Unterschiede in der Förderleistung und auf Druckeinflüsse in den Leitungen zurückzuführen ist. Trotz erreichter Sollhöhe bleiben kleine Schwankungen im Wasserstand bestehen; der Regelfehler geht nie exakt auf null. Um übermäßige Dynamik zu vermeiden, wurde der Regelfehler softwareseitig auf 1 mm (drei Nachkommastellen) gerundet.

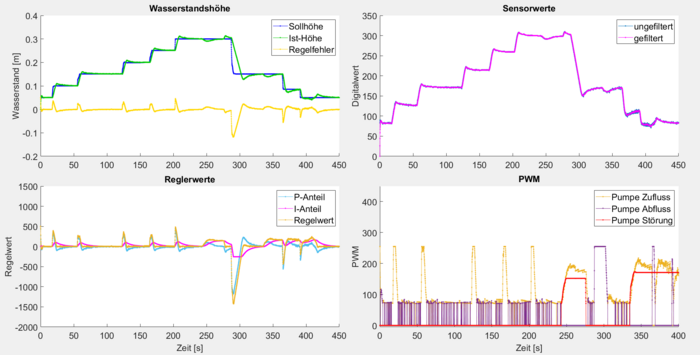
Weitere Experimente zeigten:

• Eine Frequenz von 5 Hz in Kombination mit einem höheren I-Anteil von 10000 ein besseres Regelverhalten ermöglicht.
• Dass Störungen bis 90 % zuverlässig kompensiert werden können. Bei 100 % Störung sinkt der Wasserstand ab – der Abfluss übersteigt hier den maximalen Zufluss.

Die Störkompensation mit 90 % Intensität ist somit möglich, benötigt im Test jedoch rund 70 s.

• Bei längeren Laufzeiten treten Probleme mit einer Leckage auf, welche die Langzeitstabilität und Störkompensation beeinträchtigten. Obwohl der reale Wasserstand optisch konstant blieb, sank der gemessene Wasserstand über die Zeit erheblich.
• Eine eingeschränkte Not-Aus-Funktion: Zwar wird die 12 V-Leitung zuverlässig getrennt, jedoch bleiben 5 V über den Arduino aktiv, wodurch die Pumpen bei bestimmten PWM-Werten weiterlaufen können.

Die folgende Abbildung zeigt das finale System mit den umgesetzten Erkenntnissen aus den Experimenten. Dabei wurden folgende Parameter angepasst:

• die Filter-Frequenz wurde auf 5 Hz gesetzt.
• die Reglerparameter wurden auf 𝐾ₚ = 10000 und 𝐾ᵢ = 10000 eingestellt.
• der Regelfehler wurde auf drei Nachkommastellen begrenzt.

Abbildung 16: Abschließender Systemtest

Fazit und Ausblick

Diese Arbeit zeigt die erfolgreiche Entwicklung und Umsetzung eines geregelten Wasserstandssystems für die praxisorientierte Hochschullehre.

Zusammenfassung der Ergebnisse

Das System erreicht die Sollhöhe mit einer Genauigkeit von ±5 mm, kompensiert Störungen bis 90 % zuverlässig und zeigt ein insgesamt stabiles Regelverhalten. Der eingesetzte PI-Regler arbeitet wie erwartet, auch wenn Totzeiten, Verzögerungen und ungleiche Pumpenleistungen zu Abweichungen führen.

Bei 100 % Störung sinkt der Wasserstand, da der maximale Zufluss nicht ausreicht. Zudem wurde eine Leckage in der Messkette festgestellt, wodurch der Wasserstand fälschlich als fallend angezeigt wurde.

Didaktischer Nutzen

Das System eignet sich ideal als Demonstrator für Regelungstechnik:

• Anschauliche Vermittlung von PI-Regelung und Störverhalten
• Intuitive Bedienung über Konsole und Display
• Transparenter, modularer Aufbau mit gut sichtbaren Komponenten

Optimierung und Ausblick

Verbesserungspotenzial besteht unter anderem in:

• Erweiterung des Reglers zur Echtzeit-Anpassung von Parametern
• Realistischere Modellierung von Totzeiten in der Simulation
• Überarbeitung der Not-Aus-Schaltung (auch 5 V trennen)
• Abdichtung der Messleitung für verlässliche Langzeitwerte
• Verbesserte Zuflussführung mit Rückschlagventil zur Reduktion von Wellen

Das System bildet eine robuste, erweiterbare Basis für Lehre und Weiterentwicklung.

Anhang

Masterarbeit

Masterarbeit Hilz Denim

SVN

SVN

Poster

Masterarbeit Poster Hilz Denim

Literatur

---

→ zurück zum Profil: Denim Mike Hilz