Spurerkennung

Wichtige Anmerkung!!! Das finale Fusions Programm bzw. Projekt der Bahnplanung und Spurführung mit der Objekterkennung des Lidars auf dem im nächsten Semester aufgesetzt werden sollte liegt im folgenden SVN Pfad: ....\Software\OSE_Fusion_Software_Final. Des Weiteren wurde die Erstellung einer Draufsicht in dem Wikiartikel Bildentzerrung und Koordinatentransformation beschrieben und wird im Wintersemester 2019/20 in die Objekt- und Spurerkennung implementiert werden. Dazu wird die Spurerkennung verändert werden müssen, um aus der Draufsicht die Spur sicher erkennen zu können. Die aktuelle Spurerkennung in dem Programm (Stand 19.07.2019) wird in dem Folgenden Artikel beschrieben.

Workflow und Vorgehen

Um schnellere Ergebnisse zu erzielen und ein leichteres Umsetzen der eigenen Ansätze zu ermöglichen wurde entschieden, die Algorithmen in Matlab zu entwickeln und auf Funktionalität zu prüfen. Anschließend wurden diese dann in C/C++ Code umgesetzt und in das Projekt mit eingebunden. Die folgenden Abschnitte beschreiben welche Voraussetzungen geschaffen wurden, um diesen Entwicklungsansatz umzusetzen.

Modellbasierte Entwicklung in Matlab

Matlab stellt mit seinen Toolboxen eine große Funktionsvielfalt im Bereich der Bildverarbeitung zur Verfügung. Diese erleichtern das Umsetzen von eigenen Ansetzen. Einfache Darstellung und Visualisierung vereinfachen insbesondere die Fehlersuche. Um auf der späteren Zielhardware zu funktionieren, werden die Algorithmen mit Hilfe Videos entwickelt, das mit einer Kamera aufgenommen wurde, die baugleich mit am Auto verbauten ist.

Die fertigen Algorithmen, die der Bildverarbeitung dienen, müssen so aufgebaut sein, dass sie auf Datenbasis eines S/W Kantenbildes arbeiten. Alle Funktionen, die der Umformung des Bildes dienen, müssen ausgelagert werden.

Um die in Matlab entworfenen Algorithmen in das C++ Projekt zu übernehmen, gibt es die Möglichkeit den Embedded Coder zu nutzen. Dieser ermöglicht es aus Matlab Code C / C++ Code zu generieren. Eine Anleitung zum Generieren von C Code findet sich in dem Artikel "Von Matlab zu C Code" Um den Code im "Objekt_Spurerkennung" Projekt zu verwenden, muss unter dem Punkt "Dateien ins Projekt übernehmen" des Artikels "Von Matlab zu C Code" "C/C++ Dynamic Libary" statt "C/C++ Static Libary" gewählt werden.

Bestimmte Matlab Funktionen lassen sich nicht generieren. Hier müssen eigene Funktionen in Matlab programmiert werden um diese zu ersetzen. Eine andere Möglichkeit ist das Einsetzen von Dummyfunktionen in Matlab Code. Diese Dummyfunktionen enthalten keine Funktionalität sondern dienen nur als Platzhalter deren Funktionsaufruf im C/C++ Projekt dann durch den Aufruf der jeweiligen in C / C++ umgesetzten Funktion ersetzt wird.

Umsetzung in C Code

Vorausetzungen zum übernehmen der Matlab Algorithmen

Die Grundlage des hier vorgestellten Vorgehens ist, dass die Datenbasis für beide Entwicklungsschritte gleich ist. So muss gewährleistet sein, dass die Bilder der Kamera und die aus dem in Matlab verwendeten Video einer Rundfahrt, vor dem Verwenden durch die Algorithmen zur Spur- und Stoplinienerkennung in ein einheitliches Bildformat konvertiert werden.

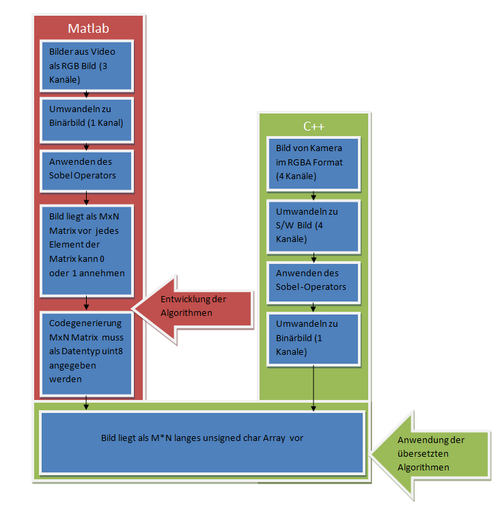
In der Matlab Umgebung werden die Video Frames mit der Auflösung 752*478 eingelesen und in die Matrix Frame gespeichert. Das in Frame gespeicherte Bild wird erst in ein Grau- und anschließend in ein S/W Bild umgewandelt. Auf dieses wird Sobel Operator angewendet. Das Ergebnis wird in Frame_bw gespeichert. Frame_bw dient allen in Matlab entwickelten Algorithmen als Datengrundlage und muss bei deren Übersetzung als uint8 Array gespeichert werden.

 % Frame lesen
    Frame = imread(Frame_Name,'PNG');
    Frame = rgb2gray(Frame);

    
 % Vorverarbeitung
    Frame_bw = Gray2BW( Frame , 752, 478 );
    Frame_bw = edge(Frame_bw,'sobel','nothinning');

Im C++ Projekt werden die Bilder von der auf dem Auto verbauten VRmagic Kamera aufgenommen. Um diese mit den Matlab Algorithmen zu bearbeiten sind noch weiter Schritte nötig.Die Abbildung 2 zeigt die Schritte aus der Software "Objekt_Spurerkennung" die zur Bildverarbeitung nötig sind.

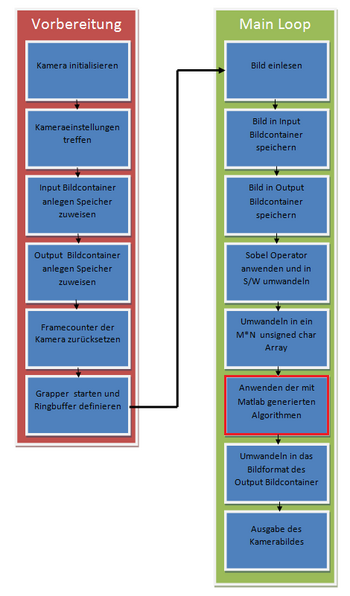
Im linken Teil des Bildes sind die Initialisierungsschritte dargestellt. Zuerst muss die Verbindung zur Kamera aufgebaut und Einstellungen wie z.B. die Belichtungszeit gesetzt werden. Anschließend werden Bildcontainer für das Quell- (p_gray_src_img) und das Ausgabebild(p_out_img) angelegt. Das Quellbild wird im Bildfromat "VRM_GRAY_8" gespeichert. Somit kann die Umwandlung von RGB zu Grau entfallen.

    VRmImage* p_gray_src_img = 0;
    VRmImageFormat gray_format;
    gray_format.m_width = 752;
    gray_format.m_height = 478;
    gray_format.m_color_format = VRM_GRAY_8;
    gray_format.m_image_modifier = 0;

 // allocation of gray level source image, use VRmUsbCamFreeImage to free images allocated with VRmUsbCam Lib
    if(!VRmUsbCamNewImage(&p_gray_src_img, gray_format))
        LogExit();

Das Ausgabebild muss in einem mit der Ausgabe auf dem Bildschirm durch die "SDL Bibliothek" kompatiblem Bildformat vorliegen. Es wird im Format "VRM_ARGB_4X8" gespeichert. Weiter Informationen über die verwendbaren Formate finden sich in der Datei "vrmusbcam2.h".

    // allocation of gray level image for output in SDL window, use VRmUsbCamFreeImage to free images allocated with VRmUsbCam Lib
    VRmImage* p_out_img = 0;
    VRmImageFormat bgr888_format;
    bgr888_format.m_width = 752;
    bgr888_format.m_height = 478;
    bgr888_format.m_color_format = VRM_ARGB_4X8;
    bgr888_format.m_image_modifier = 0;

    if(!VRmUsbCamNewImage(&p_out_img, bgr888_format))
        LogExit();

Nach dem Anlegen der Bildcontainer wird der Framecounter der Kamera zurückgesetzt und der "Grabber" zum holen der Bilder gestartet. Im Anschluss wird die Main Loop gestartet und zyklisch ausgeführt. Zu Beginn jedes Zyklus wird ein neues Bild von der Kamera geladen und anschließend in p_gray_src_img konvertiert. Um es später auszugeben wird p_gray_src_img in das Output Bildformat konvertiert und als p_out_img gespeichert.

     // lock next (raw) image for read access
        VRmImage* p_source_img = 0;
        VRmDWORD frames_dropped = 0;
        if(!VRmUsbCamLockNextImageEx(device, port, &p_source_img, &frames_dropped))
            LogExit();


     // convert source image into gray image for further processing with VM_LIB
        if(!VRmUsbCamConvertImage(p_source_img, p_gray_src_img))
            LogExit();

     // ... and copy the source image to the output image
	CopyGrayToOutRGB(p_gray_src_img, p_out_img);

Anschließend wird die Funktion "objekt_und_spurerkennung" mit dem Bilder als Parameter aufgerufen. Diese Funktion erlaubt es die aus Matlab generierten Funktionen einzubinden.

        // Kantenerkennung für die entsprechenden Zeilen
	sobel_und_bw(p_gray_src_img, p_gray_out_img, gx, gy, temp_PoI, PoI_size , on_jump );

	// Umwandeln in Bw Typ um einfache überführung von Matlab zuermöglichen 
	umwandeln_bw_bild_hin(p_gray_out_img->mp_buffer, Frame_bw_einzeilig);

	// Finde die Spurkoordinaten im ROI
	spur_finden(p_gray_src_img, Frame_bw_einzeilig, x, y, index, temp_PoI, PoI_size, on_jump,PoI_default,gx,gy);

	// Berechnung und Filterung des Schwerpunktes in X-Richtung des POI
	kalmanfilter(index, iterator, temp_PoI, PoI_default);


	Entfernung=finde_stoplinie(Frame_bw_einzeilig,&Stoplinie,&Trefferzeile);
		
	//Transformiere die Bildkoordinaten in Weltkoordinaten
	koordinatentransformation(index, x, y, Kanten_Spur_x, Kanten_Spur_y, Kanten_Spur_g);

	//Bestimme aus den Weltkoordinaten ein Polynom und verschiebe auf Sollspur
	valide_funktion = polynombestimmung(index, temp_koeff, Kanten_Spur_g ,verschiebung[iterator]);

	// Zurück Umwandeln aus Bw Typ zur Darstellung 
	umwandeln_bw_bild_zurueck(p_gray_out_img->mp_buffer, Frame_bw_einzeilig);

Zuerst wird mit Hilfe der Funktion "sobel_und_bw" der Sobel Operator auf die relevanten Zeilen des entsprechenden ROIs angewendet und ein Kantenbild erstellt. Anschließend wird durch eine Schwellwertentscheidung das Kantenbild in ein S/W Bild umgerechnet und in dem VRM_ARGB_4X8 Format des Output Bildcontainers gespeichert. Zu beachten ist hierbei der unterschiedliche "pitch" der Bildformate.Dieser gibt an wie viele Bytes einen Pixel repräsentieren. Das VRM_GRAY_8 ist ein 8 Bit Format; jeder Pixel wird durch ein Byte dargestellt. Das VRM_ARGB_4X8 ist ein 32 Bit Format; hier wird jeder Pixel durch 4 Bytes beschrieben. Dieses setzt sich aus 4 Kanälen (jeder entspricht einem Byte pro Pixel) : dem Alphakanal, dieser gibt die Transparenz an, und den 3 Farbkanälen Rot, Grün und Blau. Um das VRM_GRAY_8 in das VRM_ARGB_4X8 Format umzuwandeln, werden Daten des einen Kanals in alle 3 Farbkanäle des neuen Formats geschrieben. Da das Bild keine Transparenz besitzen soll, wird der Alphakanal auf sein Maximum gesetzt.

    p_gray_out_img->mp_buffer[(r) * p_gray_out_img->m_pitch + x * 4 + 0] = (unsigned char)grad;
    p_gray_out_img->mp_buffer[(r) * p_gray_out_img->m_pitch + x * 4 + 1] = (unsigned char)grad;
    p_gray_out_img->mp_buffer[(r) * p_gray_out_img->m_pitch + x * 4 + 2] = (unsigned char)grad;
// Alphakanal hoch setzen --> Transparenz 
   p_gray_out_img->mp_buffer[(r) * p_gray_out_img->m_pitch + x * 4 + 3] = 255;

Mit der Funktion "umwandeln_bw_bild_hin" ist es möglich das Bild aus dem VRM_ARGB_4X8 Format in ein für die mit Matlab generierten Funktionen kompatibles Bildformat umzuwandeln.

Die Funktion "spur_finden" ermittelt dann anschließend alle Spurpunkte, die sich in dem ROI befinden. Hier ist zu beachten das zu Beginn die Zeilen noch oben hin untersucht werden. Wenn die oberste Zeile des ROIs erreicht wurde, spring der Algorithmus in die erste Zeile des ROIs zurück und sucht dann den Teil unterhalb des ROIs nach möglichen Spurpunkten ab. Dieser letzte Schritt ist notwendig, da die Punkte nahe des Fahrzeuges als besonders bedeutend einzustufen sind.

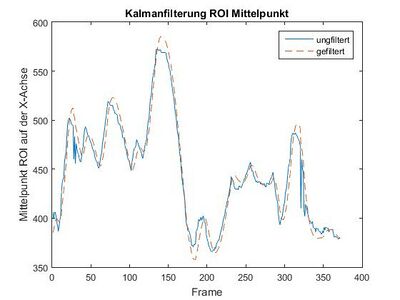
Nachdem dann alle Spurpunkte ermittelt wurden, wird mittels des Funktion "kalmanfilter" der neue Schwerpunkt des ROIs aus den gefundenen Spurpunkten berechnet und anschließend mit dem Kalmanfilters gefiltert. Denn so wandert der jeweilige ROI mit dem Spurverlauf mit und das Risiko keine Spur zu finden wird minimiert.

Die Koordinatentransformation der Bildpunkte in die Kamerakoordinaten führt die Funktion "koordinatentransformation" durch. Anschließend wird aus den realen Spurpunkten eine Polynom interpoliert mittels der Funktion "valide_funktion". Dieses Polynom wird schlussendlich noch in das Sollpolynom linksverschoben von der rechten Fahrbahnmarkierung umgerechnet.

Die Umkehrung der Funktion "umwandeln_bw_bild_hin" erlaubt die Funktion "umwandeln_bw_bild_zurueck". Um diese Funktionen nutzen zu können, muss das Bild als S/W Kantenbild im VRM_ARGB_4X8 Format bereitgestellt werden. Nach dem Umwandeln in das Ausgabeformat werden in das Bild gefundene Spurpixel Rot gekennzeichnet und das Bild ausgegeben.

Übernahme der Matlab Algorithmen

Die Struktur des C++ Projektes ermöglicht es einfach neue Module hinzuzufügen. Dies gilt sowohl für Matlab-generierte Module als auch für handgeschriebe Module wie z.B. Komunikation. Dieser Teil zeigt wie ein zuvor nach dem Artikel "Von Matlab zu C Code" erzeugtes Modul integriert wird. Nach dem Generieren liegt in dem zum generieren angelegten Projektordner der Ordner "codegen" vor. Dieser beinhaltet den Ordner "dll". Dies steht für Dynamic Link Library. Ist dies nicht der Fall muss der Code erneut als "C/C++ Dynamic Libary" generiert werden. Ist er vorhanden, enthält er den Ordner mit dem gewählten Modulnamen. Dieser wird in die in Abbildung 3 gezeigte Struktur in den Ordner Module hinzugefügt.

Anschließend müssen entweder alle Dateien aus dem Ordner bis auf "Modulname.c", "Modulname.h" und "Modulname_types.h" gelöscht werden. Oder es werden alle Dateien zur Nachvollziehbarkeit gespeichert. In das Visual Studio Projekt werden nur "Modulname.c", "Modulname.h" und "Modulname_types.h" hinzugefügt da alle anderen Daten entweder nicht relevant sind oder bereits existieren. Da das Projekt als C++ Projekt angelegt ist, muss die ".c" in eine ".cpp" Datei umbenannt werden. In Visual Studio ist das Projekt in dieselbe Struktur geteilt in der es auch im Ordner abgelegt ist. Es wird jedoch zwischen ".h" und".c"

Dateien unterschieden. Dementsprechend muss der Modulordner sowohl unter Headerdatein als auch unter Quelldateien hinzugefügt werden.

Abbildung 4: Visual Studio Projektstruktur

Anschließend muss der Modulordner als zusätzliches Inventarverzeichnis hinzugefügt werden. Dies wird in dem Menü Projekteigenschaften vorgenommen. Nach einem Rechtsklick auf Objekt_Spurerkennung (siehe Abbildung 4) öffnet sich ein Kontextmenü in dem der letzte Punkt "Eigenschaften" gewählt werden muss. Anschließend öffnet sich das gesuchte Menü.

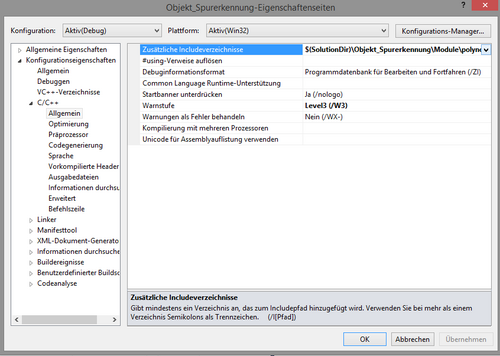
In diesem muss unter zusätzliche Inventarverzeichnisse der Modulordner hinzugefügt werden. Nachdem das Modul erfolgreich in das Projekt eingefügt wurde, müssen nun noch Code-Anpassungen vorgenommen werden. Falls in Matlab Dummyfunktionen für in C++ bereits vorhandene Funktionen eingebaut wurden, müssen diese jetzt durch ihre C++ Funktionen ersetzt werden. Ebenso müssen die Includes der Header "Modulname_initialize.h" und "Modulname_terminate.h" entfernt werden. Da bestimmte Matlab Funktionen nicht generierbar sind, kann es zu weiteren Änderungen im Code kommen. Es empfiehlt sich dies gut hervorzuheben und durch Kommentare zu rechtfertigen.

Umsetzung

Spur finden und auswerten

Damit das Fahrzeug innerhalb einer Fahrbahn geregelt fahren kann, muss in irgendeiner Form der Verlauf der Strecke wahrgenommen werden. Dies funktioniert kameragestützt. Der Ansatz zur Spurerkennung orientiert sich an den sogenannten "regions of interest" (ROI). Diese ROIs sind definierte, aber auch dynamsiche Bildauschnitte, in denen die jeweiligen Fahrbahnmarkierungen gesucht werden. Momentan ist ein ROI für die rechte und die linke Fahrbahnmarkierung implementiert. Die Mittellinie wird nicht berücksichtigt, weil sie lediglich aus unterbrochenen Abschnitten besteht. Der allgemeine Algorithmus weist folgenden Ablauf auf:

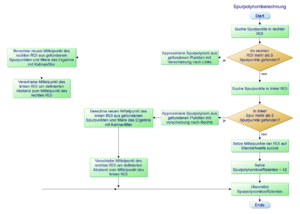
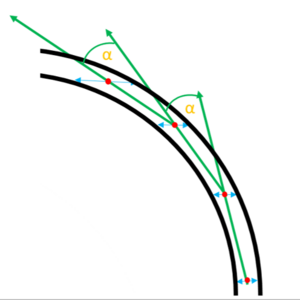
Innerhalb jedes ROIs werden dann die relevanten Punkte der Fahrbahnmarkierung bestimmt. Hierzu startet der Spurerkennungsalgorithmus mittig in der untersten Zeile des ROIs. Je nach Parametrierung (Linke Spur nach links und Rechte Spur nach rechts) werden die Zeilen dann nach rechts oder links auf mögliche Spurpunkte untersucht. Ein valider Spurpunkt muss zwei Bedingungen erfüllen. Zum einen müssen in der Zeile zwei Kantenübergänge gefunden werden, die einen maximalen und minimalen Abstand voneinander aufweisen müssen. Ist dies erfüllt wird die Mitte als vorläufiger Spurpunkt angenommen. In der darauf anschließenden Bedingung darf der Winkel zwischen dem aktuellen und dem alten Richtungsvektor nicht mehr als 45° betragen. Ist der linke bzw.rechten Rand des ROIs überschritten oder ist ein valider Spurpunkt gefunden, springt der der Algorithmus um den aktuellen Richtungsvektor verschoben intervallmäßig mittig in die nächste zu untersuchende Zeile. Werden diese beiden Bedingungen von dem vermeintlichen Spurpunkt nicht erfüllt, springt der Algorithmus in der zu untersuchenden Zeile an die Stelle direkt vor dem letzten Kantenübergang und sucht in der Zeile weiter nach der Spur. Der Algorithmus ist somit in der Lage trotz vereinzeltem Pixelrauschen in der Zeile dennoch die valide Spur zu finden.

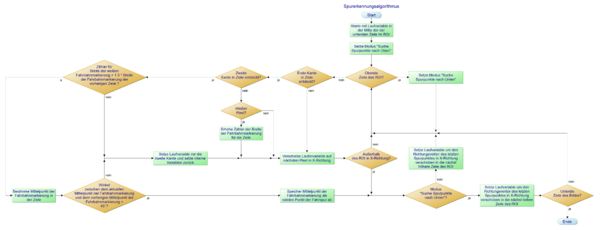
Kalman Filter

Da die Fahrbahnmarkierungen dynamisch im Kamerbild wandern, ist es sinnvoll auch die ROIs in X-Richtung des Bildes zu verschieben. Daher wird der Mittelwert aller X-Koordinaten der Fahrbahnspurpunkte eines ROIs ermittelt. Anschließend wird dieser Schwerpunkt noch mit einem Kalmanfilter gefiltert, um Sprünge und hochfrequente Verschiebungen zu dämpfen. Der Vorteil des Kalmanfilters liegt darin, dass er nicht immer den realen Werten "hinterherläuft".

Das Kalmanfilter muss für diese Anwendung nur noch parametrisiert werden, da die einzelnen Berechnungsschritte stets dieselben sind. Es wurde der Ansatz über 4 Systemzustände gewählt:

- x-Position des Schwerpunkts
- Geschwindigkeit in x-Richtung
- y-Position des Schwerpunkts
- Geschwindigkeit in y-Richtung

Die Positionen können hierbei gemessen während die Geschwindigkeiten lediglich aufgrund der Positionsänderung geschätzt werden. Dies entspricht also einem einfachen physikalischem Modell, sodass sich die Systemmatrix wie folgt gewählt wurde:

  A = [ 1  dt  0   0
        0  1   0   0
        0  0   1  dt
        0  0   0   1 ];

Dies soll als physikalische Grundlage genügen. Da somit eine Dynamik im Modell entfällt, kann die Matrix B zu Null gewählt werden. Die Messmatrix ergibt sich für die einzelnen Systemzustände zu 1 für direkt gemessene Elemente und zu 0 für lediglich indirekt beobachtete Komponenten. Um mit dem Filter gute Ergebnisse zu erzielen, muss schließlich noch betrachtet werden wie sehr das Filter den Messwerten bzw. dem System vertrauen soll. Hierbei haben diverse Versuche zu der Erkenntnis geführt, dass die folgenden Einstellungen das Filter befähigen, die Schwerpunkte auch bei schlechten Werten noch gut zu tracken und trotzdem relativ schnell auf Änderungen zu reagieren, sodass das Filter nicht den Daten "hinterhängt":

  Q = 0.01*eye(4);
  R = 0.5*[ 10  0; 0 10 ];

Der Startwert wird geschätzt. Da keine Informationen darüber vorliegen wo die Schwerpunkte zu Beginn liegen, wurde dieser Vektor zu Null gewählt. Aufgrund der oben beschriebenen guten Reaktionsfähigkeit des Filters nähert sich dieses innerhalb weniger Zyklen den wahren Werten sehr gut an.

Abbildung 9: Kalmanfilterung der ROI Mittelpunkte

Polynom berechnen

Die gefundenen Fahrbahnpunkte werden durch ein Polynom zweiten Grades interpoliert. Dabei kommt die Methode der kleinsten Fehlerquadrate zu Einsatz.

Das Spurpolynom, das durch die Kamera ermittelt wird, beschreibt den Verlauf der rechten oder linken äußeren Fahrspur. Das Fahrzeug selbst soll aber in der Mitte der rechten Fahrbahn geregelt fahren. Dafür müsste das Polynom den Verlauf der Fahrbahnmitte beschreiben. Da dort jedoch keine Daten zu ermitteln sind, muss das gefundene Polynom umgerechnet werden.

Ein sehr simpler Ansatz wäre das Polynom einfach um 20cm nach links bzw. 60 cm nach rechts zu verschieben, weil dies exakt die Hälfte der Fahrbahnbreite ist. In der Implementierung würde dies bedeuten, dass lediglich der Wert C (ax²+bx+c) um diese bestimmten cm korrigiert werden muss. Auf gerader Strecke ist diese Umformung sogar fehlerfrei. In Kurven würde dies aber Ungenauigkeiten bedeuten, da sich hier auch die Krümmungen der Parabeln für die Fahrbahnmitte und die Außenlinie unterscheiden.

Um dieses Problem zu lösen muss ein anderer Ansatz gewählt werden. Ziel ist es nun zu jedem Punkt auf der ursprünglichen Parabel den entsprechenden Punkt auf dem neuen Polynom bestimmen zu können. Dabei wird die Straßengeometrie ausgenutzt.

Zunächst wird ein Wert in das ursprüngliche Polynom eingesetzt. Dieser Wert sollte sinnvollerweise in dem Bereich liegen in dem das Polynom auch die Fahrspur beschreibt. Es ergibt sich also ein Punkt mit den Werten X und Y auf der Außenlinie. Über den korrelierenden Punkt des Zielpolynoms ist nun bekannt das er in einer euklidischen Distanz von 20cm bzw 60 cm zum Ausgangspunkt liegt. Als nächstes wird die Ableitung in diesem zuvor eingesetzten Punkt berechnet. Am Beispiel des Steigungsdreieckes zur Bestimmung von Ableitungen lassen sich die folgenden Schritte leicht erklären. Es teilt die Steigung in diesem Punkt in eine Strecke in X- und Y-Richtung ein. Da diese rechtwinkling aufeinander stehen, lassen sich die Wikelfunktionen hier anwenden. Die Strecken in X- und Y-Richtung stellen die Katheten in diesem Dreieck dar und ihr Quotient (Tangens) entspricht der Steigung, die zuvor durch Ableiten bereits ermittelt wurde. Es ist also möglich aus der Ableitung wieder die Anteile in X- und Y-Richtung zu bestimmen, indem der Arcustangens angewedet wird. Der Sinus bzw. Cosinus des hieraus resultierenden Winkels ergibt entsprechend die relative Steigung in X- bzw. Y-Richtung. Jeweils mit 20cm oder 60cm multipiziert erhält man die Werte um die der Ausgangspunkt zu verschieben ist, damit er auf dem Zielpolynom liegt.

Wiederholt man diesen Vorgang für mehrere Punkte und interpoliert durch diese anschließend eine neue Parabel, so beschreibt diese den Verlauf der Fahrbahnmitte der rechten Fahrspur.

Stopplinienerkennung

Autor: Stephan Marks

Die Stopplinienerkennung wird zunächst anhand eines vorhandenen Videos einer Fahrt auf dem Rundkurs in Form eines MATLAB-Skripts implementiert. Nach der Erprobung des Konzepts, wird der Algorithmus für die Verwendung im Fahrzeug in C-Code umgesetzt.

Vorinitialisierungen

Zu Beginn der Bildverarbeitung werden einige Vorinitialisierungen durchgeführt. Zunächst wird das Command Window der MATLAB-Benutzeroberfläche geleert, alle geöffneten Figuren geschlossen und vorhandene Variablen gelöscht. Anschließend wird eine Region of Interest (ROI) definiert, die den für die Stopplinienerkennung relevanten Bildausschnitt beschreibt. Zuletzt wird eine Figur zur Darstellung verschiedener Ausgabebilder in einem Vollbildformat initialisiert.

clc,close all,clear varibales; % Command Window leeren, Figuren schließen, Variablen löschen

%% Vorinitialisierungen

% ROI (Region of interest)
%     [xmin ymin width height]
roi = [216  225  320   100]; 

% Speicher für das Kantenbild in der Größe der ROI
edgeFrame = zeros(roi(1,4),roi(1,3));

% Figur in Vollbild
figure('units','normalized','outerposition',[0 0 1 1]);
hold on;

Einlesen des Videos

Zunächst wird die Videoaufnahme der Fahrt eingelesen. Dazu wird ein VideoReader-Objekt erzeugt. Das Video soll endlos abgespielt werden. Dazu wird innerhalb einer Endlosschleife zu Beginn überprüft, ob die Aufnahme noch unverarbeitete Einzelbilder (Frames) besitzt. Ist dies nicht der Fall, ist das Ende des Videos erreicht und die Abspielzeit wird auf den Beginn zurückgesetzt.

%% Video einlesen und einzelne Bilder verarbeiten
video = VideoReader('Rundkurs.mp4'); % Das Video muss sich im gleichen Ordner wie dieses Programm befinden.

% Einlesen des Videos in einer Endlosschleife
while true
   if ~video.hasFrame
       video.CurrentTime = 0.0;
       disp('Restart Video');
   end

Erkennung der Stopplinien

Um die Stopplinienerkennung durchzuführen wird aus der eingelesenen Videodatei ein Einzelbild entnommen. Dieses Bild wird innerhalb der vorinitialisierten Figur in Form eines Subplots dargestellt. Dieser Subplot ist in Abbildung 13 aufgeführt.

   % Frame aus Video entnehmen und als Subplot anzeigen
   frame_original = readFrame(video);
   
   subplot(1,3,1)
   imshow(frame_original);
   title('Original')

Das Einzelbild wird zur weiteren Verarbeitung auf die ROI begrenzt und in ein Graustufenbild umgewandelt.

   % Bild auf ROI begrenzen und in Grauwertbild umwandeln 
   frame_roi = rgb2gray(imcrop(frame_original,roi));

Darauf aufbauend wird durch die Verwendung des Sobel-Operators die Kanten innerhalb des Bildausschnitts extrahiert. Dieses resultierende Kantenbild, wie in Abbildung 10 veranschaulicht, wird ebenfalls in der Figur gezeigt.

Abbildung 10: Mittels Sobel-Operator extrahierte Kanten, welche aus dem ROI des Graustufenbildes gewonnen wurden.

   % Grauwertbild in Kantenbild überführen und in Figur darstellen
   frame_roi_edge = edge(frame_roi,'sobel','horizontal');
    
   subplot(1,3,2)
   imshow(frame_roi_edge);
   title('Sobel')

Hough-Transformation

Die Fahrspuren innerhalb des vorbereiteten Kantenbildes sollen durch die Hough-Transformation detektiert werden. Die Hough-Transformation nutzt die Darstellung einer Geraden in der Parameterform

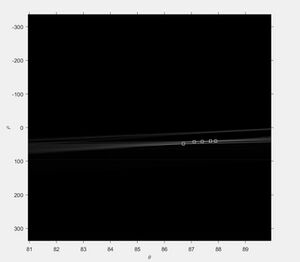
${\displaystyle \rho = x\,cos(\theta) + y\,sin(\theta) }$ .

In dieser Darstellung beschreibt $\rho$ den Betrag des Ortsvektors zu der Geraden, was der Distanz vom Koordinatenursprung zu der Geraden entspricht. Der Winkel $\theta$ stellt den Winkel des Ortsvektors im Bezug zur x-Achse des Koordinatensystems dar. Die MATLAB-Funktion hough zur Hough-Transformation gibt zusätzlich zu $\rho$ und $\theta$ die Parameterraumdarstellung in Matrixform zurück. Eine Visualisierung der Parameterraumdarstellung ist in Abbildung 11 gezeigt.

Die zu detektierenden Stopplinien zeichnen sich dadurch aus, dass diese annähernd horizontal verlaufen. Dadurch kommen ausschließlich Geraden mit einem Winkel $\theta$ in einem Intervall von

${\displaystyle \theta = [81^\circ; 89,9^\circ] }$

als Kandidaten für eine Stopplinie infrage. Die Intervallweite wurde experimentell ermittelt. Die MATLAB-Funktion hough bietet die Möglichkeit, das Winkelintervall direkt vorzugeben, sodass nur relevante Linien zurückgegeben werden.^[1]

   % Transformation mit beschränkem 'Theta', sodass nur Linien in einem
   % horizontalen Bereich betrachtet werden.   
   [H,theta,rho] = hough(frame_roi_edge,'Theta', 81:0.1:89.9);

Abbildung 11: Parameterraumdarstellung der Hough-Transformation mit den ermittelten Maxima (weiße Kästchen).

Um die Maxima der Hough-Transformation zu identifizieren, wird die Funktion houghpeaks verwendet. Dazu wird der Funktion das Ergebnis der Hough-Transformation in Matrixform sowie eine maximale Anzahl an zu ermittelnden Maxima übergeben. Zudem wird ein Schwellwert zur Definition eines Maximums vorgegeben. Hier wird der Schwellwert als 30 $\,$ % des globalen Maximums der Hough-Transformation gewählt. Die Funktion gibt anschließend die Reihen und Spalten Indizes der gefundenen Maxima innerhalb der Hough-Transformationsmatrix zurück.^[2]

   % Maxima in der Transformation ermitteln
   P = houghpeaks(H,5,'threshold',ceil(0.3*max(H(:))));

Aus den gewonnen Daten werden durch die Verwendung einer weiteren Funktion letztendlich die Linien bestimmt. Dazu werden der Funktion houghlines das Graustufenbild, die Parameter $\rho$ und $\theta$ sowie die zuvor ermittelten Indizes der bestimmten Maxima der Hough-Transformation übergeben. Darüber hinaus besitzt die Funktion die Möglichkeit, Liniensegmente über eine Lückenfüllung miteinander zu einer Gesamtlinie zu verbinden und eine Mindestlänge der gefundenen Linie festzulegen. Ein Suchbereich für die Lückenfüllung von 20 Pixeln sowie eine Mindestlänge von 150 Pixeln liefern gewünschte Ergebnisse. Die Funktion gibt die berechneten Linien mit den Attributen eines Start- und Endpunkts sowie den Parametern $\rho$ und $\theta$ zurück.^[3]

   % Linien mit einer Mindestlänge ermitteln und dabei Linenstücke
   % in bestimmten Berich verbinden
   lines = houghlines(frame_roi_edge,theta,rho,P,'FillGap',20,'MinLength',150);

Verarbeitung der ermittelten Kandidaten

Um aus den gefundenen Linienkandidaten die letztendliche Stopplinie zu bestimmen, wird die Linie ausgewählt, welche am nahesten zur Fahrzeugfront liegt. Dadurch, dass der Ursprung einer Matrix beziehungsweise eines Bildes in MATLAB in der oberen linken Ecke definiert ist, muss die Linie gefunden werden, welche den größten Abstand $\rho$ zum oberen Bildrand aufweist. Bei dieser Linie handelt es sich um die gesuchte Stopplinie.

   subplot(1,3,3)
   imshow(frame_roi), hold on;
   title('Stopplinie')
    
   % falls Linien vorhanden sind
   if ~isempty(lines)
        
        % die Linie ermitteln, die am nächsten zum Fahrzeug liegt. Diese
        % ist die gesuchte Stopplinie.
        lines_rho = [lines(:,:).rho];
        [rho_nearest_line, index_nearest_line] = max(lines_rho);
        stoppline = lines(index_nearest_line);

Für eine spätere Bestimmung des Abstands der Stopplinie zum Fahrzeug durch eine Koordinatentransformation wird der Mittelpunkt der Linie berechnet.

        % Mittelpunkt der Linie aus Startpunkt und Endpunkt berechnen 
        xy_center = stoppline.point1+(stoppline.point2-stoppline.point1)./2

Visualisierung der gefundenen Stopplinie

Für die Darstellung der detektierten Stopplinie wird diese zum einen in den Graustufenbildausschnitt und zum anderen in das ursprüngliche Originalbild eingezeichnet, wie in Abbildung 12 gezeigt. Dabei wird die Linie rot dargestellt, der Startpunkt gelb, der Endpunkt rot sowie der Linienmittelpunkt grün dargestellt. Bei der Visualisierung im Originalbild ist zu beachten, dass die Koordinatenverschiebung der Linie durch die Beschränkung auf einen Bildausschnitt mit eingerechnet wird.

Abbildung 12: Visualisierung der detektierten Stopplinie.

Abbildung 13: Darstellung der erzeugten Subplots.

        %% Visualisierung in ROI-Bild
        
        % Plot Startpunkt und Endpunkt der Stopplinie
        xy = [stoppline.point1; stoppline.point2];

        plot(xy(1,1),xy(1,2),'x','LineWidth',2,'Color','yellow');
        plot(xy(2,1),xy(2,2),'x','LineWidth',2,'Color','red');

        % Plot Mittelpunkt der Linie
        plot(xy_center(1,1),xy_center(1,2),'x','LineWidth',2,'Color','green');
        
        % Plot Stopplinie
        plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','red');
        
        %% Visualisierung in Originalbild
        
        % Umrechnung der Koordinaten des ROI-Bilds in das ursprüngliche
        % Originalbild
        xy_center_inputimage = zeros(1,2);
        
        xy_center_inputimage(1,1) = xy_center(1,1)+roi(1,1);
        xy_center_inputimage(1,2) = xy_center(1,2)+roi(1,2);
        
        stoppline_inputimage = stoppline;
        
        stoppline_inputimage.point1(1,1) = stoppline_inputimage.point1(1,1)+roi(1,1); 
        stoppline_inputimage.point1(1,2) = stoppline_inputimage.point1(1,2)+roi(1,2); 
        
        stoppline_inputimage.point2(1,1) = stoppline_inputimage.point2(1,1)+roi(1,1); 
        stoppline_inputimage.point2(1,2) = stoppline_inputimage.point2(1,2)+roi(1,2); 
        
        % Plot Startpunkt und Endpunkt der Stopplinie
        subplot(1,3,1), hold on
        xy_inputimage = [stoppline_inputimage.point1; stoppline_inputimage.point2];

        plot(xy_inputimage(1,1),xy_inputimage(1,2),'x','LineWidth',2,'Color','yellow');
        plot(xy_inputimage(2,1),xy_inputimage(2,2),'x','LineWidth',2,'Color','red');

        % Plot Mittelpunkt der Linie
        plot(xy_center_inputimage(1,1),xy_center_inputimage(1,2),'x','LineWidth',2,'Color','green');
        
        % Plot Stopplinie
        plot(xy_inputimage(:,1),xy_inputimage(:,2),'LineWidth',2,'Color','red');

   end

   pause(0.000001)
end

Laufzeit

Die Laufzeit des beschriebenen Algorithmus wird in dem folgenden Diagramm in Abbildung 14 dargestellt.

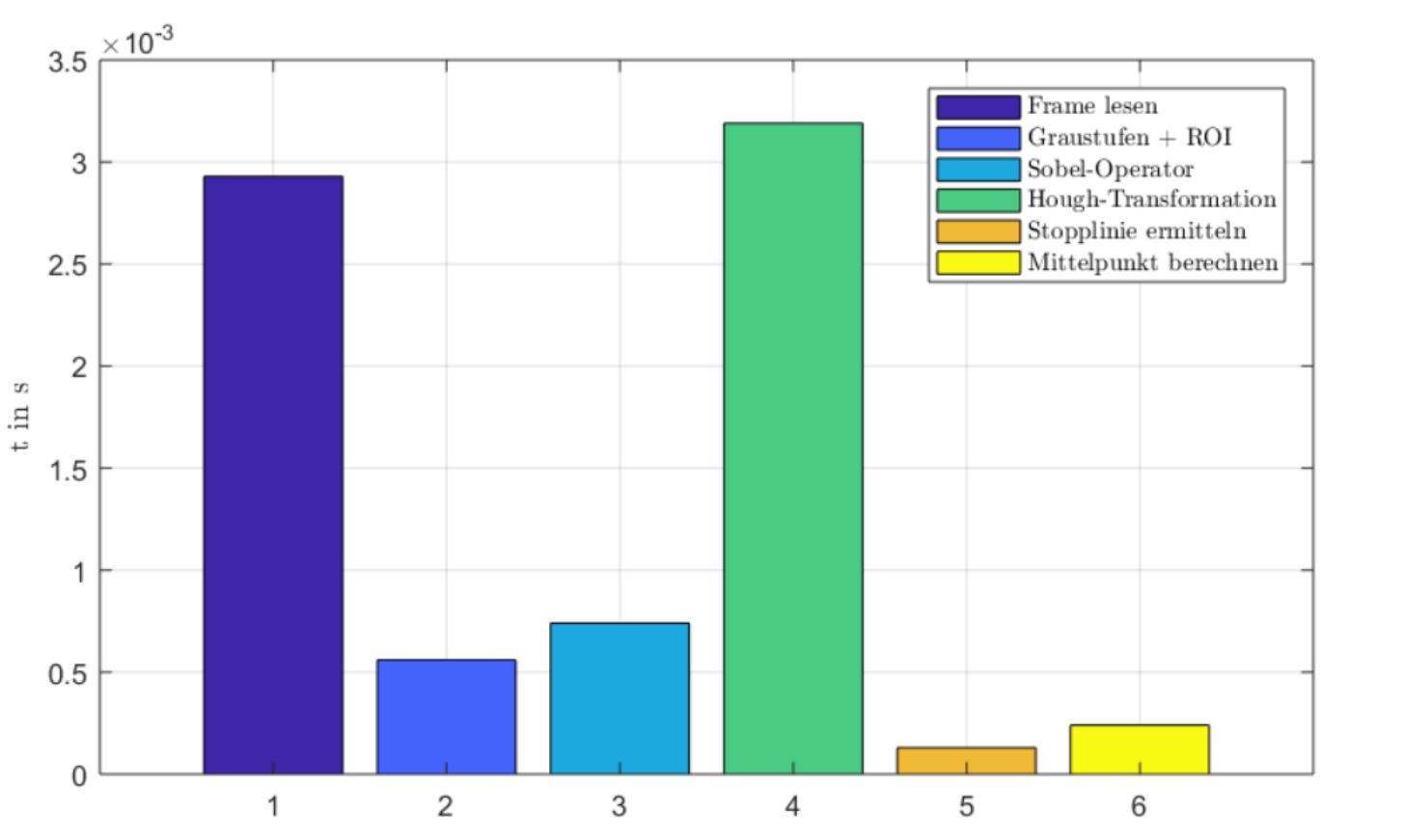
Es ergibt sich eine Gesamtlaufzeit von 0,00779 Sekunden pro Frame.

Optimierung

Abbildung 15: Detektierte Stopplinie und Markierung des Fahrbahnrandes mit Schnittpunkt (grün).

Der beschriebene Algorithmus erfüllt alle Anforderungen der Aufgabenstellung. Um die Robustheit des Algorithmus jedoch noch weiter zu erhöhen, wäre es möglich, noch weitere Merkmale einer Stopplinie zur Detektion hinzuzuziehen. Ein sich besonders anbietendes Merkmal ist die Tatsache, dass eine Stopplinie stets orthogonal zur rechten Markierung des Fahrbahnrandes verläuft. Daher besteht die Möglichkeit, diese Markierung ebenfalls durch eine Hough-Transformation zu detektieren. Durch die Berechnung des Schnittwinkels, beziehungsweise des Skalarprodukts, der Geraden in Vektorform kann eine Aussage über die Orthogonalität der Linien getroffen werden. Das Ergebnis dieser Berechnung liegt für eine sich mit der Markierung des Fahrbahnrands rechtwinkelig schneidende Stopplinie in einem Bereich von etwa $\alpha = 90^\circ$ im Falle des Schnittwinkels oder aber bei ungefähr Null für das Skalarprodukt. Eine nach diesem Prinzip detektierte Stopplinie ist in Abbildung 15 dargestellt.

Codegenerierung

Autor: Stephan Marks

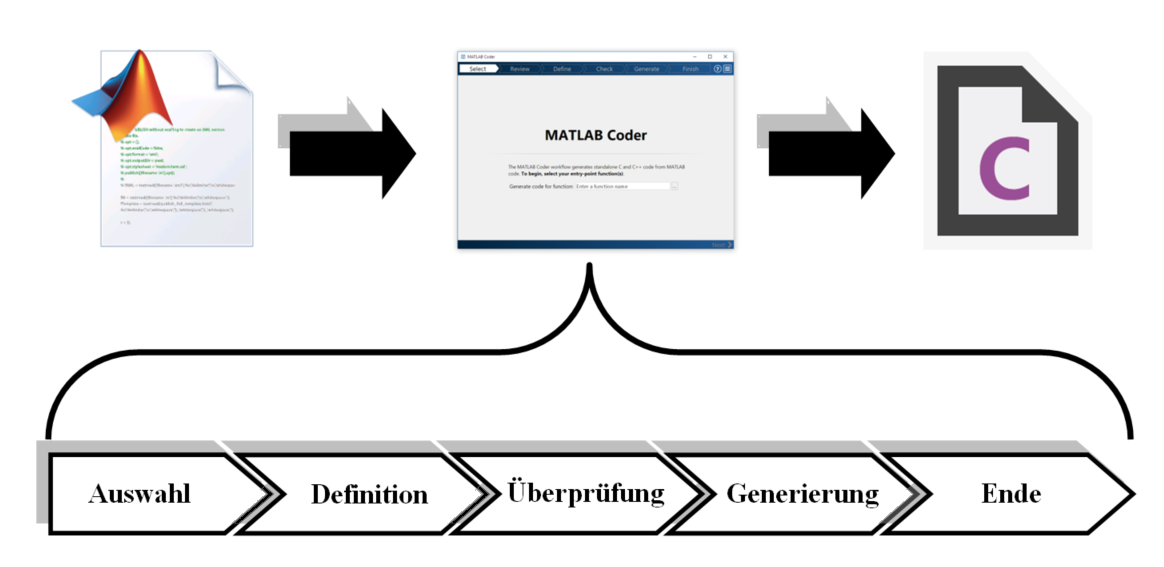
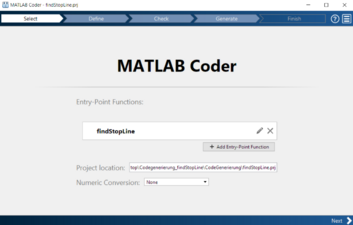
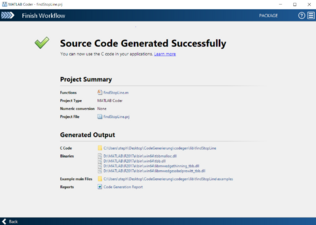
Das MATLAB-Skript zur Detektion von Stopplinien soll in die in die bestehende Software der Fahrspurerkennung integriert werden. Die Bildverarbeitungssoftware in C-Code umgesetzt. Zur Integration der Stopplinienerkennung muss demnach eine MATLAB-Funktion erzeugt werden. Aus dieser Funktion wird im Anschluss unter Verwendung der Applikation „MATLAB Coder“ C-Code generiert, der in die bestehende Bildverarbeitungssoftware eingebunden werden kann. Der Ablauf der Codegenerierung mit dem MATLAB Coder ist in Abbildung 16 visualisiert. Die Codegenerierung wird mit der MATLAB-Version 2017a durchgeführt, da diese die Umwandlung der Bildverarbeitungsfunktionen unterstützt. Zunächst wird das MATLAB-Skript in der Funktion findStopLine zusammengefasst. In dem nachfolgenden Quelltext ist die Definition des Funktionsprotypen dargestellt.

function [ stopline_center_point_x, stopline_center_point_y  ] = findStopLine( bw_image )

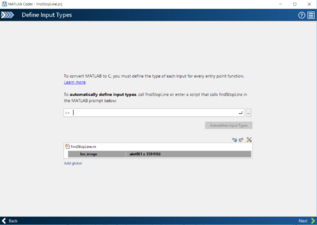
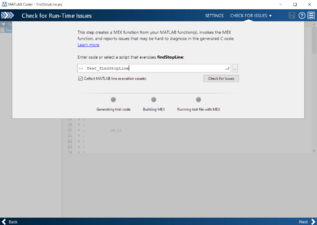
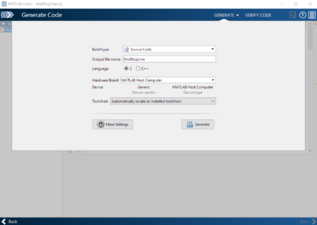
Der Funktion wird ein Graustufenbild der Fahrzeugkamera übergeben. Die Funktion gibt im Falle der Detektion einer Stopplinie die x- und y-Koordinate des Stopplinienmittelpunkts in Bildkoordinaten zurück. Wurde keine Stopplinie erkannt, wird jeweils ein Wert von -1 zurückgegeben. Die genaue Implementierung der Funktion kann im Subversion hier nachvollzogen werden. Eine Transformation der Bildkoordinaten in Weltkoordinaten ist in der Bildverarbeitungssoftware bereits vorhanden. Um die MATLAB-Funktion in eine C-Funktion umzuwandeln, wird der MATLAB Coder verwendet. Dieser führt den Benutzer in Form eines „Widzards“ durch die Codegenerierung in fünf Schritten, welche in Abbildung 17 dargestellt werden. Zu Beginn wird die MATLAB-Datei ausgewählt, welche die umzuwandelnde Funktion enthält. Anschließend werden die Übergabeparameter der Funktion manuell definiert. Hier wird das Graustufenbild der Kamera serialisiert in Form eines Arrays übergeben. Nach der Definition der Übergabeparameter erfolgt die Überprüfung der Funktion auf Laufzeitfehler. Dazu wird ein MATLAB-Skript ausgewählt, das die umzuwandelnde Funktion aufruft. Die Implementierung dieses Test-Skripts ist im Subversion hier abgelegt.

Abbildung 17: Codegenerierung mit dem MATLAB Coder
(a) Auswahl der umzuwandelnden MATLAB-Funktion.
(b) Definition der Übergabeparameter.
(c) Überprüfung der Funktion auf Laufzeitfehler.
(d) Generierung des C-Codes.
(e) Fertigstellung der Codegenerierung.

Bei der Überprüfung auf Laufzeitfehler wurde das Problem festgestellt, dass einige Programmierfeatures von MATLAB wie beispielsweise

lines_rho = [lines(:,:).rho];

nicht von der Codegenerierung unterstützt werden. Diese Programmierungen müssen zum Beisiel durch

for k = 1:size(lines,2)
    line = lines(1,k);
    lines_rho(1,k) = line.rho;
end

ersetzt werden. Anschließend kann der C-Code generiert werden.

Verhalten an Stoppkreuzungen

Autor: Stephan Marks

Wurde eine Stopplinie detektiert, muss ein Ablauf zum Halten des Fahrzeugs an der Linie initiiert werden. Das Regelwerk^[4] des Carolo-Cups sieht dabei die die folgenden Regularien vor:

Der Abstand der Fahrzeugfront zur Stopplinie muss $l_{halt} \leq 150\;mm$ betragen.
Das Fahrzeug muss für eine Dauer von $t_{halt} \geq 3\;s$ an der Stopplinie halten.
Im Falle, dass einem beweglichen Objekt Vorfahrt gewährt werden muss, hat das Fahrzeug an der Stopplinie zu warten, bis der Weg frei ist.

Zur Erstellung des entsprechenden Ablaufs wird zunächst ein Konzept erstellt.

Konzept eines Start-/Stopp-Ablaufs

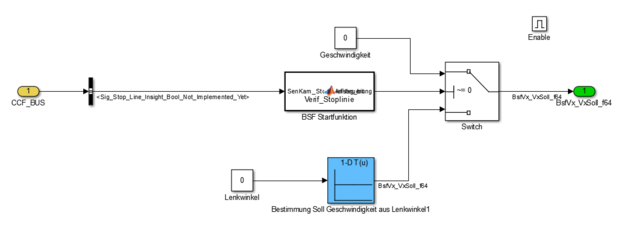
Der Start-/Stopp-Ablauf hat die Aufgabe der Längsführung im Modul der Bahnplanung und Spurführung eine Geschwindigkeit als Führungsgröße vorzugeben. Daher wird der Ablauf im Bereich der Bestimmung der Sollgeschwindigkeit eingefügt, der in Abbildung 18 dargestellt ist.

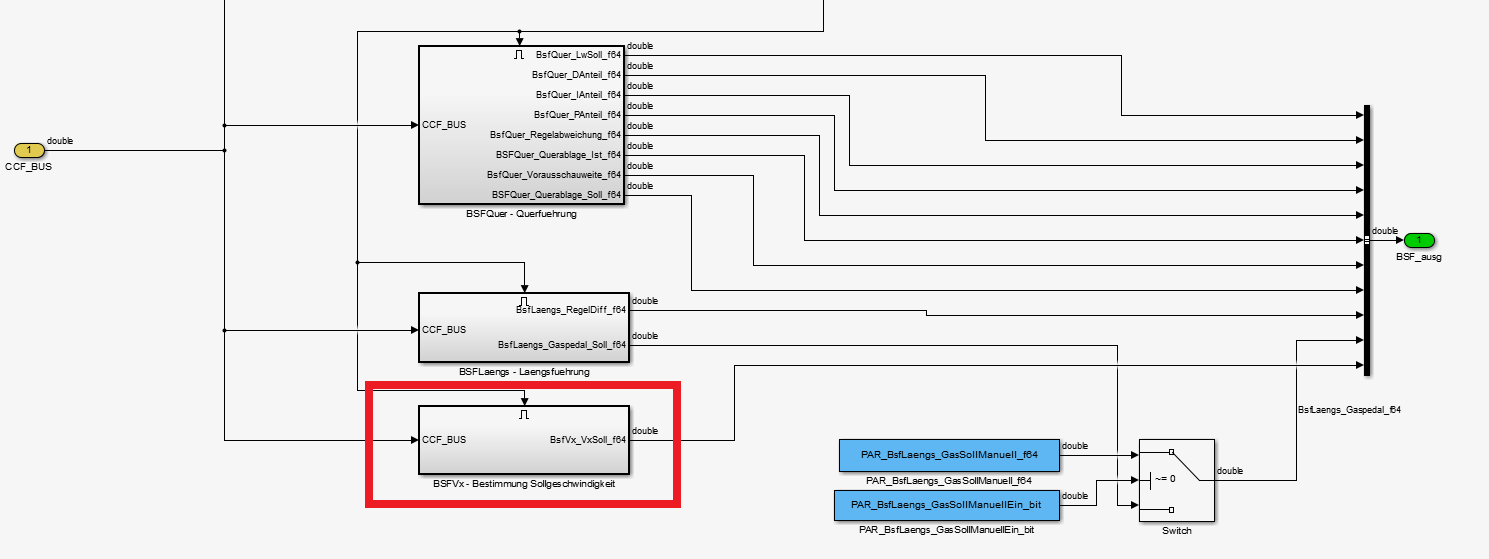
Abbildung 18: Bereich zur Bestimmung der Sollgeschwindigkeit innerhalb der Bahnplanung und Spurführung.

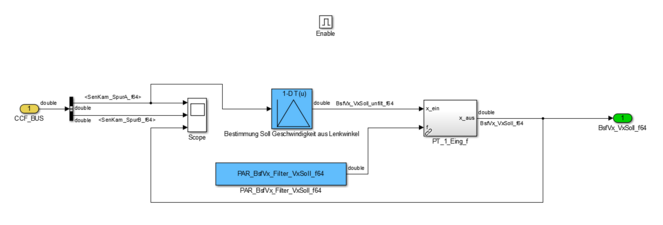
Die Sollgeschwindigkeitsbestimmung im Online-Simulink-Modell des Fahrzeugs beinhaltet den in Abbildung 19a dargestellten Signalflussplan, der sich von dem des Offline-Modells in Abbildung 19b unterscheidet. Das Online-Modell wirkt unfertig und experimentell, was für die Implementierung des neuen Ablaufs spricht. Ebenfalls ist die Sollgeschwindigkeitsbestimmung in Abhängigkeit des Lenkwinkels (vgl. Abbildung 19b) nicht vollständig enthalten. Dies sollte im Rahmen des Einfügens des Start-/Stopp-Ablauf angeglichen werden.

Abbildung 19: Sollgeschwindigkeitsbestimmung innerhalb der Bahnplanung und Spurführung.
(a) Sollgeschwindigkeitsbestimmung im Online-Simulink-Modell.
(b) Sollgeschwindigkeitsbestimmung im Offline-Simulink-Modell.

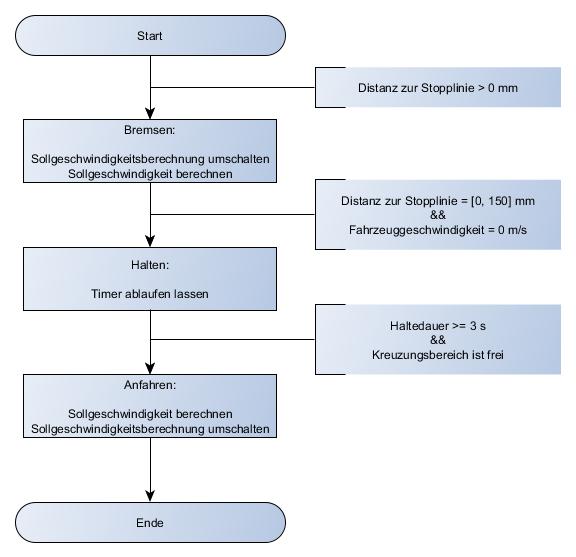
Abbildung 20: FSM zur Steuerung des Start-/Stopp-Ablaufs.

Der Start-/Stopp-Ablauf wird in Form einer Finite State Machine (FSM) implementiert, wie in Abbildung 20 dargestellt ist. Diese besitzt die drei Zustände

Bremsen,
Halten und
Anfahren.

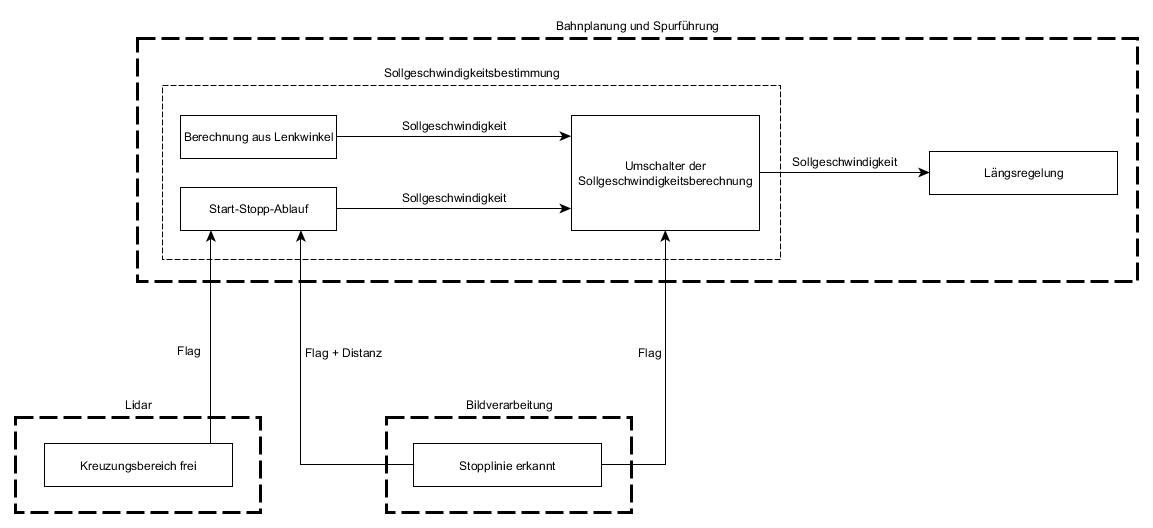
Der Ablauf wird gestartet sobald eine Stopplinie detektiert wurde. Dies ist der Fall, wenn die Distanz zur Linie $l_{halt} \ge 0\;mm$ beträgt. Ist diese Bedingung erfüllt, wird die Sollgeschwindigkeitsbestimmung von der Berechnung in Abhängigkeit des Lenkwinkels (vgl. Abbildung 19) auf die Berechnung in Abhängigkeit der Distanz zwischen der Fahrzeugfront und der Stopplinie $l_{halt}$ umgeschaltet. Gilt für die Distanz zur Stopplinie $0\;mm \le l_{halt} \le 150\;mm$ , muss das Fahrzeug stoppen. Um keine Vollbremsung durchführen zu müssen, bietet es sich an, durch eine Funktion $f$ eine sich verringernde Sollgeschwindigkeit zu berechnen. Dabei ist $v_{soll} = f(l_{halt})$ . Für $f(l_{halt})$ kann im einfachsten Fall eine linear fallende Funktion gewählt werden. Zusätzlich ist zu beachten, dass durch den Aufbau des Fahrzeugs die Stopplinie nach einer gewissen Annäherung verdeckt wird. Deshalb muss bei der Wahl von $f(l_{halt})$ berücksichtigt werden, dass bis zum vollständigen Anhalten des Fahrzeugs keine Distanz zur Stopplinie vorhanden ist. Hat das Fahrzeug gestoppt, wechselt der Ablauf in den Zustand "Halten". In diesem wird ein Timer auf eine Zeit von $t_{halt} = 3\;s$ gesetzt und gestartet. Nach Ablauf des Timers wird kontrolliert, ob der Kreuzungsbereich frei von Hindernissen ist. Ist dies der Fall, so wird in den Zustand "Anfahren" gewechselt. Um das Fahrzeug anfahren zu lassen wird den Geschwindigkeitsregler ein neuer Sollwert als Führungsgröße vorgegeben. Die Schnittstellen des Start-/Stopp-Ablaufs sind in dem Modulplan in Abbildung 21 dargestellt. Die Überprüfung, ob der Kreuzungsbereich frei ist wird von der Hinderniserkennung des Lidars signalisiert. Die Stopplinienerkennung ist im Bereich der Bildverarbeitung verankert, während sich der Ablauf selbst in der Sollgeschwindigkeitsbestimmung der Bahnplanung und Spurführung befindet.

Abbildung 21: Modulplan des Start-/Stopp-Ablaufs.

Umsetzung des Start-/Stopp-Ablaufs

Autor: Stephan Marks

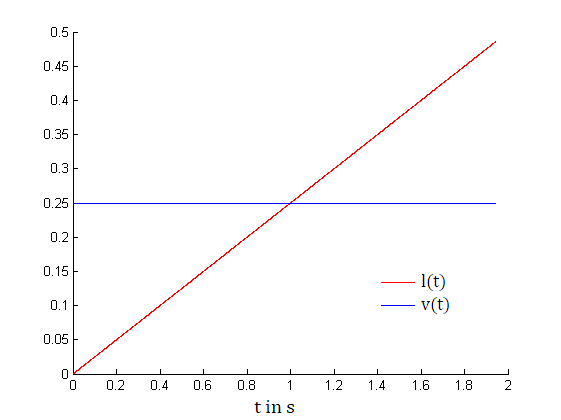
Abbildung 21: Berechnung der zurückgelegten Strecke.

Der zuvor beschriebene Start-/Stopp-Ablauf wird in Simulink als Stateflow-Graph implementiert. Dieser setzt sich aus den drei Zuständen entsprechend Abbildung 20 zusammen. In dem ersten Zustand "Bremsen" wird die Sollgeschwindigkeit des Fahrzeugs in Abhängigkeit der Distanz des Fahrzeugs zu der detektierten Stopplinie. Da nur die momentane Geschwindigkeit verfügbar ist, muss die zurückgelegte Strecke $l$ seit dem Erkennen der Stopplinie berechnet werden. Dies wird durch die Integration der momentanen Fahrzeuggeschwindigkeit über die Zeit

{\displaystyle l(t) = \int v(t)\;\mathrm{d}t }

beziehungsweise für eine diskrete Abtastung mit dem Abtastschritt $k$

{\displaystyle l(k) = l(k-1)+v(k)\;dt }

erreicht. Die Berechnung der zurückgelegten Strecke für eine konstante Geschwindigkeit ist in Abbildung 21 gezeigt. Die Sollgeschwindigkeit berechnet sich anschließend nach der Funktion

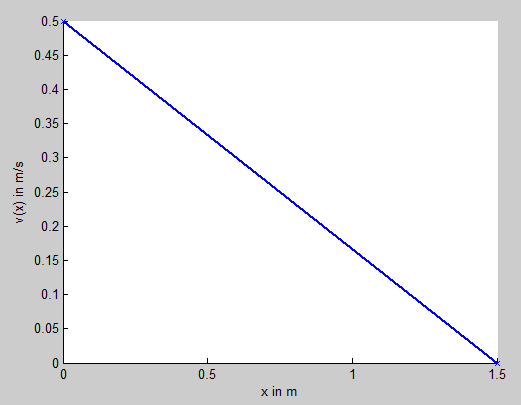
Abbildung 22: Verlauf der berechneten Sollgeschwindigkeit.

{\displaystyle v_{soll}(k) = -\frac{v(0)}{l_{halt}(0)}\;l(k)+v(0) }

,

wodurch sich der in Abbildung 22 dargestellte Verlauf der Sollgeschwindigkeit ergibt. Die weitere Umsetzung des Start-/Stopp-Ablaufs steht noch aus.

Weitere Ansätze

Kalman Filter

Die bisherige Spurerkennung ist stark fehleranfällig für fehlende Spurelemente. Diese können aufgrund von Lichtreflexen oder Lücken in der Fahrspur entstehen. Um die Spurerkennung robust gegenüber solchen Störungen zu gestalten, wird im folgenden ein Ansatz beschrieben, der die gefundenen Punkte einer Spur auf einen Schwerpunkt reduziert, diesen Mithilfe des Kalman Filters trackt und im nächsten Zyklus nur im Bereich des geschätzten Schwerpunktes sucht. Sollte keine Spurinformation in diesem Bereich vorhanden sein, wird der Wert durch den Kalman Filter bereitgestellt.

Schwerpunkte tracken

Der Schwerpunkt liegt in Form eines Koordinatenpaares (x/y) vor und soll nun getrackt werden. Dies wird mit Hilfe eines Kalman Filters umgesetzt. Dieses muss für diese Anwendung nur noch parametrisiert werden, da die einzelnen Berechnungsschritte stets dieselben sind. Wir wählen also den Ansatz das unser System über 4 Zustände verfügt:

- x-Position des Schwerpunkts
- Geschwindigkeit in x-Richtung
- y-Position des Schwerpunkts
- Geschwindigkeit in y-Richtung

Die Positionen können hierbei gemessen werden während die Geschwindigkeiten lediglich aufgrund der Positionsänderung geschätzt werden. Dies entspricht also einem einfachen physikalischem Modell, sodass sich die Systemmatrix wie folgt erstellen lässt:

  A = [ 1  dt  0   0
        0  1   0   0
        0  0   1  dt
        0  0   0   1 ];

Dies soll als physikalische Grundlage genügen. Da somit eine Dynamik im Modell entfällt, kann die Matrix B zu Null gewählt werden. Die Messmatrix ergibt sich für die einzelnen Systemzustände zu 1 für direkt gemessene Elemente und zu 0 für lediglich indirekt beobachtete Komponenten. Um mit dem Filter gute Ergebnisse zu erzielen, muss schließlich noch betrachtet werden wie sehr das Filter den Messwerten bzw. dem System vertrauen soll. Hierbei haben diverse Versuche zu der Erkenntnis geführt, dass die folgenden Einstellungen das Filter befähigen, die Schwerpunkte auch bei schlechten Werten noch gut zu tracken und trotzdem relativ schnell auf Änderungen zu reagieren, sodass das Filter nicht den Daten "hinterhängt":

  Q = 0.01*eye(4);
  R = 0.5*[ 10  0; 0 10 ];

Der Startwert kann nun geschätzt werden. Da keine Informationen darüber vorliegen wo die Schwerpunkte zu Beginn liegen, wurde dieser Vektor zu Null gewählt. Aufgrund der oben beschriebenen guten Reaktionsfähigkeit des Filters nähert sich dieses innerhalb weniger Zyklen den wahren Werten sehr gut an.

Kamerabild

Teil des Autos im Kamerabild

Durch die Position der Kamera auf dem Auto, ist ein Teil des Autos auch im Kamerabild sichtbar (siehe rote Einfärbung im Bild). Diese Informationen können sich im laufe der Bildverarbeitung als störend erweisen und ein Spur oder Start/Stopp Linien erkennen erschweren.

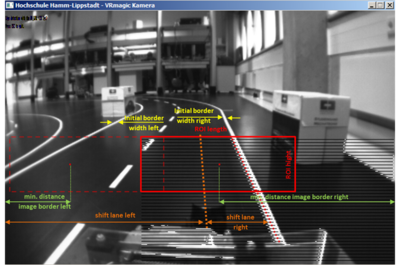
Aktuelle Lösung: "ROI und abgeklebeter LIDAR Sensor"

Durch den aktuell verwendeten ROI an der rechten und linken Fahrbahnbegrenzung, der überhalb des im Kamerabild sichtbaren Bereichs vom Auto liegt, wurde auf eine Maske im Form einer Binärmatrix, wie sie beim Vorgängeransatz verwendet wurde, verzichtet. Lediglich die weiße Haube des LIDAR-Sensors wurde mittel dunklem Klebebandes abgeklebt.

Vorherige Lösung: "Maske für das Auto"

Um eine Fehlinterpretation der Daten zu verhindern und die Spur oder Start/Stopp Linien Erkennung zu erleichtern ist es Sinnvoll diese Bildinformationen zu entfernen. Ein Ansatz der in Matlab bereits erfolgreich getestet wurde ist das Verwenden einer passenden Maske. Eine Binärmatrix die im Bereich des Autos mit Nullen und sonst mit Einsen besetzt ist und die Dimension der Bild Matrix besitzt. Nach einer Multiplikation der Matrizen sind alle Bildinformationen über das Auto entfernt.

Konfiguration

Während der Arbeiten an dem Auto im Wintersemester 16/17, ist eine Möglichkeit geschaffen worden einige wichtige Parameter für die Objekt-& Spurerkennung mit Hilfe einer Konfigurationsdatei einfach zu konfigurieren. Dies brachte den Vorteil, dass das Programm nach Parameteränderungen nicht immer neu kompiliert werden musste. Die Konfigurationsdatei wird dabei automatisch im Startvorgang des Programms eingelesen und die dort konfigurierten Parameter werden von dem Programm übernommen. Falls keine Konfigurationsdatei vorhanden ist werden fest einprogrammierte Standardwerte verwendet. Falls keine Konfigurationsdatei vorliegt, oder Parameter falsch benannt sind wird eine Fehlermeldung in der Konsolenausgabe ausgegeben.
Die Umsetzung zum Einlesen und Überprüfung der Konfigurationsdatei, sowie der Parametrierung der Standardwerte werden von den Dateien ConfigurationFileReader.cpp und ConfigurationFileReader.h in der Objekt-& Spurerkennung übernommen.

konfigurierbare Parameter

Spurerkennung:
showImage: Videobildausgabe AN/AUS
showConsoleOutput: Anzeige der Polynomparameter in der Konosle AN/AUS
blackwhite_threshold: Schwellwert für die Kantenerkennung
initial border width right: Breite der Fahrbahnbegrenzung rechts (zur Erkennung der Fahrbahnbegrenzung rechts)
initial border width left: Breite der Fahrbahnbegrenzung links (zur Erkennung der Fahrbahnbegrenzung links)
ROI length: Breite der ROIs
ROI hight: Höhe der ROIs
ROI pitch: Abstand zwischen ROI links ud ROI rechts
min. distance image border right: mindest Abstand des rechten ROIs zum rechten Bildrand
min. distance image border left: mindest Abstand des linken ROIs zum linken Bildrand
shift lane rigth: Polynomverschiebung nach links (wird verwendet wenn die rechte Fahrspurbegrenzung zum tracken der Spur verwendet wird)
shift lane left': Polynomverschiebung nach rechts (wird verwendet wenn die linke Fahrspurbegrenzung zum tracken der Spur verwendet wird)
LIDAR:
active: LIDAR AN/AUS
COMport: COMport des LIDAR
plot_active: LIDAR Objekte Plot AN/AUS

Erstellung und Ablage der Konfigurationsdatei

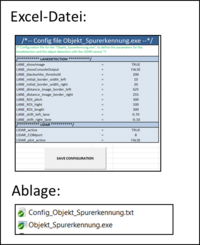
Zur einfachen Erstellung der Konfigurationsdatei wurde eine Excel-Datei erstellt mit der die einfache Erzeugung einer Konfigurationsdatei ermöglicht wird. Die Excel-Datei befindet sich im Projektordner mit dem Objekt-&Spurerkennungs Programm.

Damit die Konfigurationsdatei eingelesen werden kann, muss sich diese mit der Objekt-&Spurerkennungs Executable in einem Ordner befinden! (vgl. Bild: Excel-Tool und Ablageort)

Neuprogrammierung des ConfigurationFileReader WS18/19

Nachdem die Module des ConfigurationFileReader(.cpp/.h) nicht versioniert wurden, konnte das laut Wiki neuste Projekt nicht mehr kompiliert werden. Um dem nächsten Semester die Möglichkeit zu geben mit dem neusten Projekt weiter zu arbeiten und drauf aufsetzten zu können wurde der ConfigurationFileReader neu programmiert und in das Projekt eingefügt.

Nachfolgend noch einige Erläuterungen zum neuen ConfigurationFileReader:

Der Configuration FileReader versucht wie oben beschrieben das Textfile einzlesen, ist dies nicht vorhanden werden Standartwerte verwendet. Diese sind per #define angelegte Werte und können in der ConfigurationFileReader.h geändert werden.

/* ------------------------------------ DEFAULT PARAMETERS ---------------------------------------------------------- */
/* ----------------------------------------------------------------------------------------------------------------- */
/* Lidar default parameters */
#define LIDAR_DEFAULT_ACTIVE		    true				
#define LIDAR_DEFAULT_COMPORT		    4				
#define LIDAR_DEFAULT_PLOTACTIVE	    true			

/* Lanedetection default parameters */
#define LANE_DEFAULT_SHOWIMAGEACTIVE        true						
#define LANE_DEFAULT_SHOWCONSOLEACTIVE	    true
#define LANE_DEFAULT_BLACKWHITE             200
#define LANE_DEFAULT_BORDERWIDTHLEFT        10 
#define LANE_DEFAULT_BORDERWIDTHRIGHT       20
#define LANE_DEFAULT_DISTANCEBORDERLEFT	    625	
#define LANE_DEFAULT_DISTANCEBORDERRIGHT    125	
#define LANE_DEFAULT_ROIPITCH               300
#define LANE_DEFAULT_ROIHIGHT               100
#define LANE_DEFAULT_ROILENGTH              300
#define LANE_DEFAULT_SHIFTLEFTLANE	    -0.7		
#define LANE_DEFAULT_SHIFTRIGHTLANE	     1.0

Zusätzlich wurde eine Funktion hinzugefügt, welche das Programm anhält nachdem die eingelesenen Parameter in der Konsole dargestellt werden, damit der BEnutzer die Möglichkeit hat diese zu kontrollieren. Das Programm läuft weiter, wenn die eingelesenen Variabeln oder Defaultwerte per Enter Taste bestätigt werden.

Inverse Perspective Mapping

Bei der Verwendung einer Kamera zur Fahrspurerkennung ergibt sich immer das Problem der perspektischen Verzerrung. Grund dafür ist, dass bei der Projektion aus dem 3D-Weltkoordinatensystem in das 2D-Koordinatensystem des Bildes Information verloren gehen. Das Inverse Perspective Mapping (IPM) bietet eine Möglichkeit die verloren gegangenen Daten zu rekonstruieren und das Bild in entzerrter Vogelperspektive darzustellen.

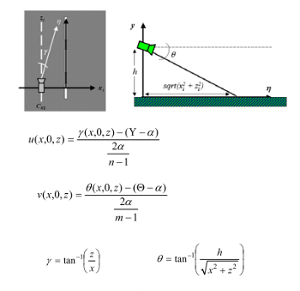
Dabei wird das Bild unter Verwendung von geometrischen Beziehungen aus dem Weltkoodinatensystem W = {(x,y,z)} in ein volgelperspektivisches Bild I = {(u,v)} transformiert. Dabei ist die die y-Komponente, wie auch in der Abbildung zu sehen ist, stets 0. Das liegt daran das eindeutige Zuordnung der Punkte nicht ohne Weiteres möglich, da schließlich Informationen verloren gegangen sind. Da hierbei Straßenlinien gefunden werden sollen, kann die Annahme getroffen, dass alle Punkte auf dem Boden und damit auf y = 0 liegen müssen. Im Fall nicht ebenen Straßen gilt diese Annahme nicht und fürht daher zu Fehlern. Das bedeutet, dass das IPM beispielsweise bei Straßen in Gebirgen nicht geeignet ist. Auch möglicherweise vor einem fahrende andere Fahrzeuge liegen nicht in der Bodenebene und sind in der Vogelperspektive verzerrt dargestellt. Der Abstand zu ihnen kann aber bestimmt werden. Außerdem müssen damit das IPM fehlerfrei funktioniert noch andere Anforderungen erfüllt sein. Position und Ausrichtung der Kamera müssen bekannt sein und es muss der Punkt auf dem Horizont fokussiert werden in dem sich die Fahrspuren zu schneiden scheinen, was wiederum erfordert, dass die Straße in der Mitte des Bildes liegt. Ist das nicht der Fall erhält man keine einwandfreien Ergebnisse, da die Straße immer noch eine perspektivische Verzerrung aufweist.

Ein Beispiel für gutes Ergebnis des IPM ist in Abbildung 20 zu sehen. [1]

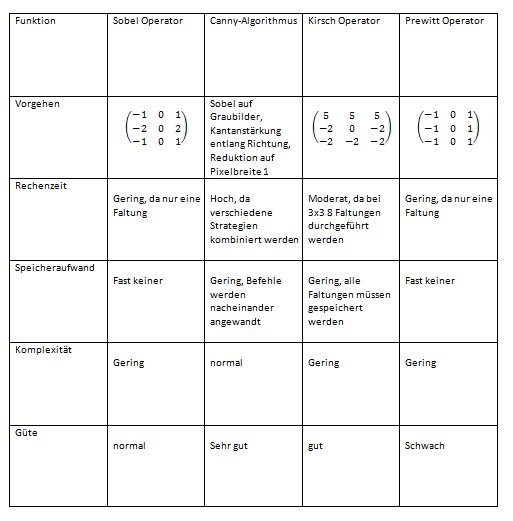
Operatoren zur Kantenerkennung im Vergleich

Quellen weiterführende Links

[1] SVN\SDE_Praktikum\Literatur\Inverse Perspective Transformation: ipm_paper_direkt
"Decomposing and composing a 3×3 rotation matrix" [1]
"Grundlegende mathematische Verfahren der 3D-Visualisierung"[2]
"Caltech Lane Detection Software"[3]
"Rekonstruktion 3D - Koordinaten aus Kamerabild"[4]

Fazit & Ausblick

Wintersemester 16/17
Fazit: Das Carolo-Cup Fahrzeug ist in der Lage die Spur sicher zutracken und zu verfolgen. Die Mittelline findet im aktuellen Ansatz keine Verwendung, nur die rechte und linke Fahrbahnbegrenzungen werden zur Spurerkennung und Polynomberechnung verwendet. Bei einer Unterbrechenung der Fahrbahnbregrenzung wechselt der Spurerkennungsalgorithmus automatisch die zu verfolgende Linie (statt ROI rechts wird ROI links verwendet).
Des Weiteren wurde eine Stopplineneerkennung implementiert, die bei einer Stopplinien-Detektion ein Bit setzt und eine Distanz an die DeepSpace-Karte übergibt.

Ausblick:

Stopplinienerkennung muss noch überarbeitet/ verbessert werden. Stopplinien werden zur Zeit nicht immer sicher erkannt. Aus Zeitgründen konnte leider keine genaue Ursache erforscht werden. Bei Test mit stehendem Auto konnte eine Stoppline immer sicher erkannt werden. Im folgenden Semester sollte nochmal genau analysiert werden warum die Stopplinie nicht immer sicher erkannt wird während das Fahrzeug fährt. Dabei ist zu prüfen, ob das Objekt-& Spurerkennungs-Programm die Stopplinie sicher erkennt und die an das Simulink-Model übergebenen Parameter von dem dort richtig ausgewertet und interpretiert werden, um einen Stopp-Vorgang am Auto einzuleiten.

Archiv bisheriger Arbeit

Zentralperspektive "Umrechnung von Bild- zu Weltkoordinaten" (aktuell verwendeter Ansatz)

Einzelnachweise

↑ MathWorks Documentation: hough Website der MathWorks Dokumentation zur Hough-Transformation. Abgerufen am 30. Juni 2018.
↑ MathWorks Documentation: houghpeaks Website der MathWorks Dokumentation zur Identifikation von Spitzen einer Hough-Transformation. Abgerufen am 30. Juni 2018.
↑ MathWorks Documentation: houghlines Website der MathWorks Dokumentation zum Ermitteln con Liniensegmenten auf Basis einer Hough-Transformation. Abgerufen am 30. Juni 2018.
↑ Basic-Cup Regulations 2018 Reglewerk des Carolo-Cups "Basic-Cup Regulations 2018". Abgerufen am 09. November 2018.

→ zurück zum Hauptartikel: Praktikum SDE

[1] MathWorks Documentation: hough Website der MathWorks Dokumentation zur Hough-Transformation. Abgerufen am 30. Juni 2018.

[2] MathWorks Documentation: houghpeaks Website der MathWorks Dokumentation zur Identifikation von Spitzen einer Hough-Transformation. Abgerufen am 30. Juni 2018.

[3] MathWorks Documentation: houghlines Website der MathWorks Dokumentation zum Ermitteln con Liniensegmenten auf Basis einer Hough-Transformation. Abgerufen am 30. Juni 2018.

[4] Basic-Cup Regulations 2018 Reglewerk des Carolo-Cups "Basic-Cup Regulations 2018". Abgerufen am 09. November 2018.

[1]

[2]

[3]

[4]

Alter Ansatz OSE-Objekt- und Spurerkennung

Spurerkennung

Workflow und Vorgehen

Modellbasierte Entwicklung in Matlab

Umsetzung in C Code

Vorausetzungen zum übernehmen der Matlab Algorithmen

Übernahme der Matlab Algorithmen

Umsetzung

Spur finden und auswerten

Kalman Filter

Polynom berechnen

Stopplinienerkennung

Vorinitialisierungen

Einlesen des Videos

Erkennung der Stopplinien

Hough-Transformation

Verarbeitung der ermittelten Kandidaten

Visualisierung der gefundenen Stopplinie

Laufzeit

Optimierung

Codegenerierung

Verhalten an Stoppkreuzungen

Konzept eines Start-/Stopp-Ablaufs

Umsetzung des Start-/Stopp-Ablaufs

Weitere Ansätze

Kalman Filter

Schwerpunkte tracken

Kamerabild

Teil des Autos im Kamerabild

Aktuelle Lösung: "ROI und abgeklebeter LIDAR Sensor"

Vorherige Lösung: "Maske für das Auto"

Konfiguration

konfigurierbare Parameter

Erstellung und Ablage der Konfigurationsdatei

Neuprogrammierung des ConfigurationFileReader WS18/19

Inverse Perspective Mapping

Operatoren zur Kantenerkennung im Vergleich

Quellen weiterführende Links

Fazit & Ausblick

Archiv bisheriger Arbeit

Zentralperspektive "Umrechnung von Bild- zu Weltkoordinaten" (aktuell verwendeter Ansatz)

Spurerkennung (vorheriger Ansatz)

Objekterkennung mit Laserscanner

Objekterkennung mit RP Lidar A1M8

Objekterkennung mit Kamera

Einzelnachweise

Navigationsmenü