Regelung des Radschlupfes eines Modellautos

Abb. 1: Skizze eines 3-rädrigen Fahrzeugs mit Geschwindigkeiten, Ortsvektoren und Koordinatensystemen zur Herleitung des kinematischen Fahrzeugmodells.

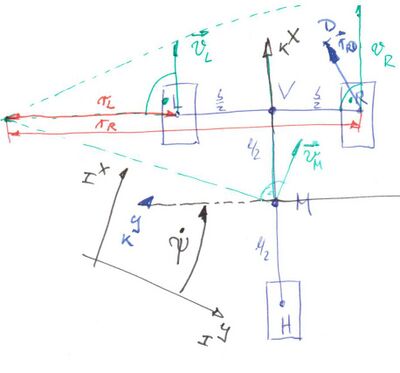
Autoren: Mario Wollschläger, Lukas Honerlage

Anforderungen

Tabelle 1: Testbare, atomare Anforderungen

ID	Inhalt	Ersteller	Datum	Geprüft von	Datum
1	Das Fahrzeugmodell muss die Kinematik des als starr angenommenen Fahrzeugkörpers beschreiben.	Prof. Göbel	07.06.2017	Prof. Schneider	08.06.2017
2	Das Fahrverhalten muss unter der Annahme korrekt abgebildet werden, dass die Räder schlupffrei abrollen.	Prof. Göbel	07.06.2017	Prof. Schneider	08.06.2017
3	Am Eingang werden die Längsgeschwindigkeiten entlang der x-Achse des Fahrzeugkoordinatensystems K der Räder rechts (R) und links (L) vorgegeben.	Prof. Göbel	07.06.2017	Prof. Schneider	08.06.2017
4	Am Ausgang müssen die Position und Geschwindigkeit des Mittelpunktes M und des frei definierbaren Punktes D in x- und y-Richtung des Inertialsystems I der Gierwinkel und die Gierrate zur Verfügung stehen.	Prof. Göbel	07.06.2017	Prof. Schneider	08.06.2017
5	Das Modell muss in Matlab/Simulink erstellt werden.	Prof. Göbel	07.06.2017	Prof. Schneider	08.06.2017
6	Die Rechnung des Modells erfolgt mit diskreten Zeitschritten (es sind diskrete Integratoren zu verwenden).	Prof. Göbel	07.06.2017	Prof. Schneider	08.06.2017
7	Die Dokumentation muss auf Basis der Mehrkörpersystemeberechnung leicht nachvollziehbar erfolgen.	Prof. Göbel	07.06.2017	Prof. Schneider	08.06.2017
8	Bei der Simulation muss eine graphische Ausgabe der Position und Richtung des Fahrzeugs in x- und y-Koordinaten des I-Systems erfolgen.	Prof. Göbel	07.06.2017	Prof. Schneider	08.06.2017
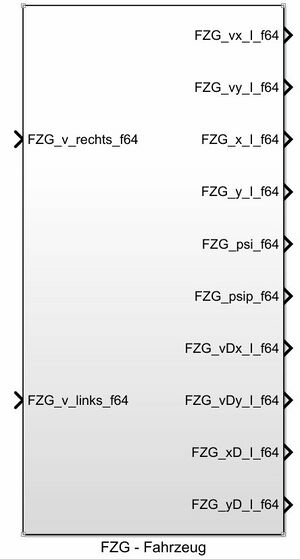
9	Die Signalnamen müssen gemäß nebenstehender Abbildung gewählt werden.	Prof. Göbel	07.06.2017	Prof. Schneider	08.06.2017

Tabelle 1 zeigt die funktionalen Anforderungen und Abb. 2 die Anforderungen an die Schnittstellen des Moduls.

Abb. 2: Schnittstellen für die Modellierung eines 3-rädrigen Fahrzeugs mit Geschwindigkeiten, Ortsvektoren und Koordinatensystemen.

Programmierung

Die Programmierung ist nun auf Basis der oben ermittelten Gleichungen möglich und erfolgt in Matlab/Simulink.

Matlab

Über ein Start-Skript werden alle relevanten Parameter gesetzt und das Modell geöffnet.

%%%
%%% Simulation des Ardumower-Fahrzeugs
%%%
%%% Prof. Mirek Göbel, 08.06.2017

%% Initialisierung
clc; clear; close all;


%% Einstellungen
PAR_Darstellung_Schalter_EIN_bit = 1;
Simulinkmodus = 1;
addpath ../Hauptprogramm/funktionen/;
addpath ../Hauptprogramm/libraries/;
addpath ../Hauptprogramm/parameter/;


%% Parameter
PAR_FZG_spurweite_f64 = 0.4; % in m
PAR_FZG_radstand_f64 = 0.4; % in m
PAR_FZG_abstand_sensor_VA_f64 = 0.23; % Abstand des Perimeter-Sensors von der Vorderachse in m
T = 0.01; % Schrittweite für die Simulation (gilt für das ganze Modell)
PAR_VIS_Anzahl_Schritte_n = 10; % Angabe, alle wieviel Schritte etwas dargestellt werden soll

% Startwinkel
PAR_FZG_psi0_I_f64 = 0; % Start-Gierwinkel in rad
cospsi =  cos(PAR_FZG_psi0_I_f64); % zur Abkürzung / Vermeidung von Schreibarbeit (s. u.)
sinpsi =  sin(PAR_FZG_psi0_I_f64); % zur Abkürzung / Vermeidung von Schreibarbeit (s. u.)

% Startweg des Mittelpunktes M
PAR_FZG_x0_I_f64 = 0; % Start-x-Weg in m
PAR_FZG_y0_I_f64 = 0.5; % Start-y-Weg in m


% Startweg des Punktes D
r_MDx_K = PAR_FZG_radstand_f64/2 + PAR_FZG_abstand_sensor_VA_f64;
r_MDy_K = PAR_FZG_spurweite_f64/2 + 0;
PAR_FZG_xD0_I_f64 = PAR_FZG_x0_I_f64 + cospsi*r_MDx_K + sinpsi*r_MDy_K; % Start-x-Weg des Punktes D in m
PAR_FZG_yD0_I_f64 = PAR_FZG_y0_I_f64 - sinpsi*r_MDx_K + cospsi*r_MDy_K; % Start-y-Weg des Punktes D in m


%% Modell auf!
open('fahrzeugmodell2017a.slx');

Komponententest

Da es sich bei dieser Entwicklung um die einer einzelnen Komponente handelt, schließt der Komponententest mit dem Testbericht die Entwicklung ab (vgl. Tabelle 2).

Tabelle 2: Testbericht für den Komponententest

ID	Testfallbeschreibung	Eingang $_Kv_{Lx} [\mbox{m/s}]$	Eingang $_Kv_{Rx}[\mbox{m/s}]$	Erwartetes Ergebnis	Testergebnis	Testperson	Datum
1	Das Fahrzeugmodell steht.	0	0	Alle Ausgänge sind Null.	OK	Prof. Göbel	10.06.2017
2	Das Fahrzeugmodell fährt eine Rechtskurve.	1	0	Rechtskurve: Negative Gierrate, negativer Gierwinkel.	OK	Prof. Göbel	10.06.2017
3	Das Fahrzeugmodell fährt eine Linkskurve.	0	1	Linkskurve: Positive Gierrate, positiver Gierwinkel.	OK	Prof. Göbel	10.06.2017
4	Das Fahrzeugmodell fährt geradeaus.	1	1	Keine Gierrate und Gierwinkel, $_Kv_M = _Kv_L = _Kv_R$.	OK	Prof. Göbel	10.06.2017

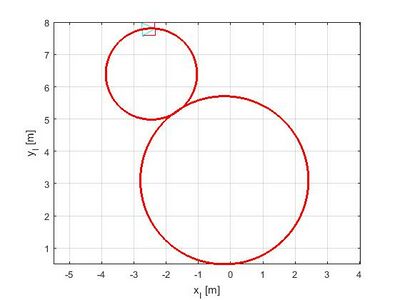
Als Abschluss dieses Artikels zeigt Abb. 6 eine Ergebnisdarstellung der Fahrzeugbewegung in I-Koordinaten (Draufsicht).

Abb. 6: Ergebnisdarstellung für die Modellierung eines 3-rädrigen Fahrzeugs in einer x-y-Draufsicht

Zusammenfassung

Das Modell ist fertig und funktioniert wie gewünscht! Somit ist die Entwicklung von Algorithmen möglich, ohne ein Fahrzeug in Hardware zur Verfügung zu haben. Dadurch eröffnen sich ernorme Möglichkeiten wie z. B. simultanes Entwickeln, automatisiertes Testen, simulative Auslegung von Reglern u. s. w.!

Literaturverzeichnis

---

→ zurück zum Hauptartikel: