ArduMower: Kartierung in Matlab/Simulink
Autor: Prof. Dr.-Ing. Schneider
Einleitung
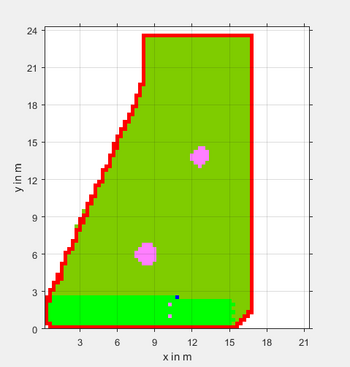
Dieser Artikel beschreibt den Aufbau einer Matrix-basierten Karte zur Darstellung des aktuellen Mähstandes eines Rasenmähroboters. Der Anstoß zur Entwicklung dieser Karte lieferte das Projekt "ArduMower", in dem der Kollege Prof. Göbel und der Autor dieses Artikels mit Studierenden gemeinsam einen autonomen Rasenmäher entwickeln, siehe Projekt_ArduMower.
Das systematische Vorgehen bei der Entwicklung des Modells orientiert sich am V-Prozessmodell.
Anforderungen
Im Lastenheft des Projektes ArduMower wird die Erstellung einer selbstlernenden Karte gefordert:

Im Pflichtenheft taucht daraufhin der Punkt Selbstlernende Karte auf, konkrete Anforderungen an werden jedoch nicht näher spezifiziert:

Folgende Anforderungen wurden an die Karte gestellt:
| ID | Inhalt | Ersteller | Datum | Geprüft von | Datum |
|---|---|---|---|---|---|
| 1 | Die Karte muss als Matrix mit der Rastergröße 30cm umgesetzt werden (Grid-Map). | Prof. Schneider | 18.01.2018 | Hr. Kreuer | 18.01.2018 |
| 2 | Die Perimeterschleife muss rot markiert werden. | Prof. Schneider | 18.01.2018 | Hr. Kreuer | 18.01.2018 |
| 3 | Die aktuelle Position des Mähers muss Blau markiert werden. | Prof. Schneider | 18.01.2018 | Hr. Kreuer | 18.01.2018 |
| 4 | Hindernisse müssen magenta markiert werden. | Prof. Schneider | 18.01.2018 | Hr. Kreuer | 18.01.2018 |
| 5 | Unbekannte Bereiche müssen weiß bleiben. | Prof. Schneider | 18.01.2018 | Hr. Kreuer | 18.01.2018 |
| 6 | Ungemähter Rasen muss dunkelgrün und gemähter Rasen hellgrün markiert werden. | Prof. Schneider | 18.01.2018 | Hr. Kreuer | 18.01.2018 |
| 7 | Die Karte muss zyklisch aktualisiert werden. | Prof. Schneider | 18.01.2018 | Hr. Kreuer | 18.01.2018 |
| 8 | Die Umsetzung muss als Matlab-Skript erfolgen, so dass eine Einbindung in Simulink als Matlab-Funktion möglich ist. | Prof. Schneider | 18.01.2018 | Hr. Kreuer | 18.01.2018 |
| 9 | Eingangsgrößen der Funktion Kartenfunktion.m sind
|
Prof. Schneider | 18.01.2018 | Hr. Kreuer | 18.01.2018 |
| 10 | Ausgangsgrößen der Funktion Kartenfunktion.m sind
|
Prof. Schneider | 18.01.2018 | Hr. Kreuer | 18.01.2018 |
| 11 | Die Initialisierung muss 1s und die zyklische Darstellung muss 1ms unterschreiten. | Prof. Schneider | 18.01.2018 | Hr. Kreuer | 18.01.2018 |
| 12 | Bei Kommentierung und Dokumentation muss sich an die Projektrichtlinien gehalten werden. | Prof. Schneider | 18.01.2018 | Hr. Kreuer | 18.01.2018 |
Funktionaler Systementwurf / Technischer Systementwurf
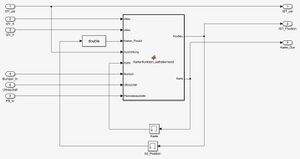
Bei der Größe des zu erstellenden Modells werden die Schritte Funktionaler Systementwurf/Technischer Systementwurf des V-Modells zusammen gelegt und bereits Schnittstellen zwischen den einzelnen Blöcken definiert.
Komponentenspezifikation
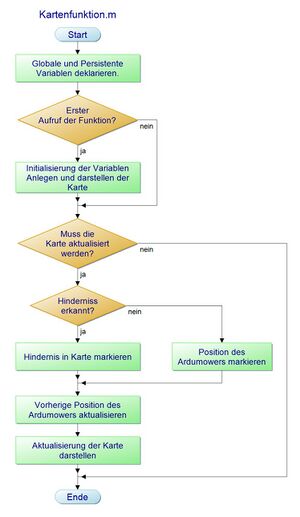
Das Modell wird insgesamt als Komponente aufgefasst, d. h. die einzelnen Blöcke aus dem Systementwurf werden als Bestandteil der Komponente "Selbstlernende Karte" definiert. Die Funktion der Komponente "Selbstlernende Karte" wird in Form eines PAP spezifiziert.
Programmierung
die Programmierung unterscheidet sich
- in die Initialisierung und
- die zyklische Aktualisierung
der selbstlernenden Karte.
Initialisierung
In der einmaligen Initialisierung werden die Farben der Karteninhalte entsprechend der Anforderungen festgelegt. Die aColorMap wird anderen Programmteilen als globale Variable zur Verfügung gestellt.
% Farben festlegen
cUnbekannt = [1 1 1]; nUnbekannt = 0;
cPerimeter = [1 0 0]; nPerimeter = 1;
cNichtGemaeht = [0.5 0.8 0]; nNichtGemaeht = 2;
cGemaeht = [0 1 0]; nGemaeht = 3;
cArduMower = [0 0 1]; nArduMower = 4;
cHindernis = [1 0.5 1]; nHindernis = 5;
aColorMap = [ cUnbekannt ; cPerimeter ; cNichtGemaeht ; cGemaeht ; cArduMower ; cHindernis ];
Die Karte wird aus einer Datei geladen und in Form und Größe initialisiert. Hierzu gehört auch die beschriftung der Achsen und die Darstellung des Gitters in Meter. Die Handles hierzu werden persistent gespeichert.
Karte = imread('libraries/mKarte.png'); % Karte laden
%% Karte in Größe und Form initialisieren
mKarte = Karte; % Ursprüngliche Karte sichern
hKarte = figure;
set(hKarte,'WindowStyle', 'normal')
hImg = imshow(Karte,aColorMap); set(gca,'YDir','normal');
hAxes = gca;
set(hKarte,'Position',[1 1 500 600],'OuterPosition',[ 550 300 500 600]); % 589
set(hAxes,'OuterPosition',[-0.1068 0 1.1819 1])
set(hAxes,'Visible','on')
xt = 0: 10:size(Karte, 2)-1;
yt = 0: 10:size(Karte, 1)-1;
for i=1:length(xt)
xtLabel{i}=num2str(xt(i)*0.3);
end
for i=1:length(yt)
ytLabel{i}=num2str(yt(i)*0.3);
end
set(gca, 'xgrid', 'on', 'ygrid', 'on', 'xtick', xt, 'ytick', 1/2+yt, 'xticklabel', xtLabel, 'yticklabel', ytLabel)
xlabel('x in m'); ylabel('y in m');
Aktualsierung
Bei der Bestimmung der Geschwindikeit in M wird mit dem Satz "räumliche Bewegung" die bekannte Geschwindigkeit in R, der Relativdrehvektor der Koordinatensysteme K gegenüber I sowie der Ortsvektor zwischen R und M verwendet (siehe [1]):
Im körperfesten Koordinatensystem K beschrieben folgt eine Beschreibung, in der jeder Term selbst 3 Komponenten (x, y, z) enthält und mit denen jetzt im jeweiligen Koordinatensystem gerechnet werden kann (das ging bei der vektoriellen Schreibweise oben noch nicht!).
Mit den eingetragenen Komponenten sieht die Gleichung wie folgt aus:
Zur Bestimmung der Gierrate wird obiger Ansatz erneut verwendet, um von der bekannten Geschwindigkeit in R auf die ebenfalls bekannte Geschwindikeit in L "zu schließen", sodass der Relativdrehvektor der Koordinatensysteme K gegenüber I in K-Koordinaten bestimmt werden kann (jetzt mit Komponenten besser Spaltenmatrix genannt: ). Es folgt:
.
Mit eingesetzten Komponenten ergibt sich im körperfesten System K:
.
Aus Zeile 1 der obigen Gleichung kann die Gierrate (selbstverständlich im körperfesten System K) mit nachstehendem Zusammenhang ermittelt werden.
Umgestellt folgt daraus:
Um die Position des Punktes M in Inertialkoordinaten zu berechnet, wird seine Geschwindigkeit in Intertialkoordinaten I benötigt, da diese dann durch eine einfache Integration in die Position überführt werden kann. Im körperfesten System ist dies nicht erlaubt bzw. möglich, da dieses sich dreht! Mit Hilfe einer Transformationsmatrix kann diese Umrechnung in einem Schritt erfolgen.
Der über den Ortsvektor von R nach D beliebig wählbare Punkt D kann genauso wie oben der Mittelpunkt M behandelt werden. Die Gleichungen in Kurzform dazu sind wie folgt.
Im körperfesten Koordinatensystem K beschrieben folgt eine Beschreibung, in der jeder Term selbst 3 Komponenten (x, y, z) enthält und mit denen jetzt im jeweiligen Koordinatensystem gerechnet werden kann (das ging bei der vektoriellen Schreibweise oben noch nicht!).
Das Ergebnis für D lautet:
.
Komponententest
Da es sich bei dieser Entwicklung um die einer einzelnen Komponente handelt, schließt der Komponententest mit dem Testbericht die Entwicklung ab.
| ID | Testfallbeschreibung | Eingang | Eingang | Erwartetes Ergebnis | Testergebnis | Testperson | Datum |
|---|---|---|---|---|---|---|---|
| 1 | Das Fahrzeugmodell steht. | 0 | 0 | Alle Ausgänge sind Null. | OK | Prof. Göbel | 10.06.2017 |
| 2 | Das Fahrzeugmodell fährt eine Rechtskurve. | 1 | 0 | Rechtskurve: Negative Gierrate, negativer Gierwinkel. | OK | Prof. Göbel | 10.06.2017 |
| 3 | Das Fahrzeugmodell fährt eine Linkskurve. | 0 | 1 | Linkskurve: Positive Gierrate, positiver Gierwinkel. | OK | Prof. Göbel | 10.06.2017 |
| 4 | Das Fahrzeugmodell fährt geradeaus. | 1 | 1 | Keine Gierrate und Gierwinkel, . | OK | Prof. Göbel | 10.06.2017 |
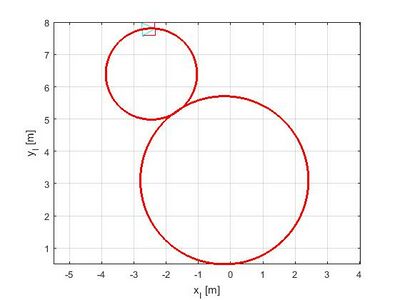
Als Abschluss zeigt die letzte Abbildung dieses Artikels eine Ergebnisdarstellung der Fahrzeugbewegung in I-Koordinaten (Draufsicht).
Zusammenfassung
Das Modell ist fertig und funktioniert wie gewünscht! Somit ist die Entwicklung von Algorithmen möglich, ohne ein Fahrzeug in Hardware zur Verfügung zu haben. Dadurch eröffnen sich ernorme Möglichkeiten wie z. B. simultanes Entwickeln, automatisiertes Testen, simulative Auslegung von Reglern u. s. w.!
Literaturverzeichnis
- ↑ M. Göbel: Formelsammlung Mehrkörpersysteme und Robotik, HSHL, Version 29.06.2017
→ zurück zum Hauptartikel: Projekt ArduMower