Signalverarbeitende Systeme - L10: Koordinatentransformation

Dozent:	Prof. Dr.-Ing. Schneider
Lehrveranstaltung:	Signalverarbeitende Systeme
Modul	Signalverarbeitende Systeme und Systems Design Engineering
Modulbezeichnung:	BSE-M-2-1.06
Modulverantwortung:	Prof. Ulrich Schneider
Vorlesung:	Invertierter Klassenraum, Montag, 10:00 - 11:30 Uhr
Übung:	Montag, 11:45 - 12:30 Uhr
Ort:	Labor L3.1-E00-120

Übung 10.1: KOS-Trafo: Rotation+Translation, Inverse Transformation

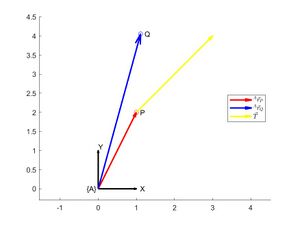
Das Lösungsvideo finden Sie auf der Lernplattform. Gegeben is der Ortsvektor zum Punkt P ${}^A{\overrightarrow{r}}_P$ sowie der Rotationswinkel $\gamma =50^{\circ }$ um die Z-Achse.

1. Führen Sie über eine homogene Translation eine Rotation um den Winkel $\gamma$ und eine Translation um den Vektor $\overrightarrow{T}$ aus.
2. Zeichnen Sie den transformierten Punkt Q und dessen Ortsvektor ${}^A{\overrightarrow{r}}_Q$ ein (vgl. Abb. 1).
3. Berechnen Sie anschließend die inverse Translation ${}^A{\overrightarrow{r}}_{P,2}$

Gegeben sind:

• ${}^A{\overrightarrow{r}}_P=\left(\begin{array}{c}1\\ 2\\ 3\end{array}\right)$
• $\overrightarrow{T}\left(\begin{array}{c}2\\ 2\\ 0\end{array}\right)$
• $\gamma =50^{\circ }$

Abb. 1: Ergebnisdarstellung der Übung 10.1

Musterlösung 10.1 

%% Gegeben
A_r_P = [1;2;3;1]; % Ortsvektor zum Punkt P in KOS A

% Translation
T = [2;2;0]'; % Translationsvektor
S = 1;        % Skalierungsfaktor
P = [0 0 0];  % Perspektiventrafo
Gamma = 50;   % Rotationswinkel im deg
R = [cosd(Gamma) -sind(Gamma) 0;sind(Gamma) cosd(Gamma) 0; 0 0 1];   % Rotationsmatrix

D = zeros(4,4); % Homogene Transformation
D(1:3,1:3)= R;
D(1:3, 4) = T;
D(4,4)    = S;
D(4,1:3)  = P

A_r_Q = D * A_r_P % KOS-Trafo

%% Inverse Transformation
A_r_P2 = inv(D)*A_r_Q

%% Ergebnisdarstellung
figure
hold on
quiver(0,0,1,0,'LineWidth',2,'Color','black','AutoScale','off'); % x-Achse
text(1.1,0,'X')
quiver(0,0,0,1,'LineWidth',2,'Color','black','AutoScale','off'); % y-Achse
text(0,1.1,'Y')
h1 = quiver(0,0,A_r_P(1),A_r_P(2),'LineWidth',2,'Color','r','AutoScale','off'); % Ursprungsvektor
plot(A_r_P(1),A_r_P(2),'ro')
text(A_r_P(1)+0.1,A_r_P(2),'P')
h2 = quiver(0,0,A_r_Q(1),A_r_Q(2),'LineWidth',2,'Color','b','AutoScale','off'); % Vektor nach Trafo
text(A_r_Q(1)+0.1,A_r_Q(2),'Q')
plot(A_r_Q(1),A_r_Q(2),'bo')
h3 = quiver(A_r_P(1),A_r_P(2),T(1),T(2),'LineWidth',2,'Color','y','AutoScale','off'); % Translationsvektor
axis equal
legend([h1,h2,h3],{'$^A\vec{r}_P$','$^A\vec{r}_Q$','$\vec{T}$'},'Interpreter','latex','Location','east')
text(-0.3,0,'\{A\}')
ylim([-0.3 4.5])

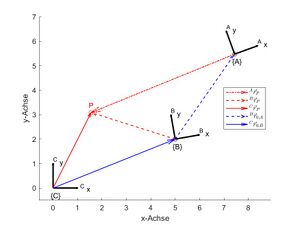
Übung 10.2: 2-fache Koordinatentransformation

Das Lösungsvideo finden Sie auf der Lernplattform.

Gegeben sind:

• ${}^A{\overrightarrow{r}}_P=\left(\begin{array}{c}-6,3411\\ -0,2345\\ -3\end{array}\right)$: Ortsvektor zum Punkt P im KOS A
• ${}^B{\overrightarrow{r}}_{0,A}=\left(\begin{array}{c}3\\ 3\\ 0\end{array}\right)$: Translationsvektor KOS B zum KOS A im B-KOS
• ${}^C{\overrightarrow{r}}_{0,B}=\left(\begin{array}{c}3\\ 3\\ 0\end{array}\right)$: Translationsvektor KOS C zum KOS B im C-KOS
• KOS A ist gegenüber KOS B um 10° um die Z-Achse gedreht.
• KOS B ist gegenüber KOS C um 10° um die Z-Achse gedreht.

Aufgaben:

• Bestimmen Sie die Vektoren ${}^B{\overrightarrow{r}}_P$ und ${}^C{\overrightarrow{r}}_P$.
• Erstellen Sie ein Ergebnisbild gemäß Abb. 2.

Abb. 2: Ergebnisdarstellung der Übung 10.2

Musterlösung 10.2  Das Lösungsvideo finden Sie auf der Lernplattform.

Übung 10.3: Transformationsarithmetik

Datei:Transformationsarithmetik MobileRobotik.jpg Datei:SigSys L10 3 KOS Trafo.jpg

Musterlösung 10.3  Das Lösungsvideo finden Sie auf der Lernplattform.

---

→ zurück zum Hauptartikel: BSE Signalverarbeitende Systeme
→ weiter zum Artikel: Signalverarbeitende Systeme - SoSe25