Auslegung der Reglerparameter
Update Juni 2014
Nachdem eine Messung des Geschwindigkeitssignals am Fahrzeug vorgenommen und das System angepasst wurde, wurden folgende Parameter festgelegt:
- P-Anteil: 3
- I-Anteil: 1
- D-Anteil: 0
- Windup-Faktor: 10
Update Januar 2015
Nachdem das ESM angepasst war, wurde zuerst mit deutlich kleineren Werten gearbeitet. Da jedoch die Reaktionszeit mit I-Anteil zu langsam war, wurden folgende Parameter festgelegt:
- P-Anteil: 0.5
- I-Anteil: 0
- D-Anteil: 0
- Windup-Faktor: 1
Wind-Up

Die Stellgröße für das Gaspedal ist gemäß Anforderung auf das Intervall [-1 1] begrenzt. Aus diesem Grund ist im Simulink-Modell ein entsprechender Begrenzungsblock eingefügt, der den Wert des Regler-Ausgangs von -1 bis 1 begrenzt. Bei PI-Reglern mit einer derartigen Begrenzung tritt der Wind-Up-Effekt auf. Prof. Dr.-Ing. Frank Allgöwer beschreibt diesen folgendermaßen:
Bei einem Regler mit I-Anteil wird z.B. der so entstehende zusätzliche Regelfehler aufintegriert. Es folgt ein starkes Überschwingen, das bis zur Instabilität führen kann.[1]
Im vorliegenden Modell wurde in der genannten separaten Simulations-Umgebung ein hoher Sprung als Sollgröße simuliert, vgl. Abbildung Windup-Problematik: Vergleich Soll- und Istgröße und Reglerparameter im Diagramm oben links. Das Aufintegrieren des I-Anteils kann dabei sehr gut beobachtet werden (Diagramm unten rechts in der Abbildung). Die Reaktion auf ein entsprechend niedrigeres Signal erfolgt dabei mit einer gewissen Totzeit, da der hohe I-Anteil erst abgebaut werden muss. Dieses ist im Plot der Ist-Geschwindigkeit (mitte links in der Abbildung) zu sehen.
Die Lösung dieser Problematik wird im Allgemeinen mit einer Anti-Windup-Strategie erreicht, die erstmalig aktiv wird, wenn Sättigung auftritt, also wenn der Regler-Ausgang größer ist als die begrenzte Stellgröße.[2]
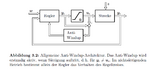

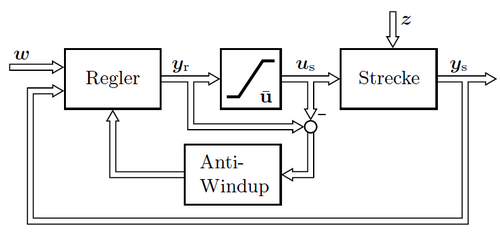
Quelle: "Entwurf von modellbasierten Anti-Windup-Methoden für Systeme mit Stellbegrenzungen" von A. Ortseifen. S. 28. (Link Abruf: 14.05.2014)
Wie in der Abbildung erkenntlich, wird dazu einfach der Wert am Ausgang des Reglers um den Wert nach der Begrenzung verringert. Die Abbildung Allgemeine Anti-Windup-Strategie mit Bildtext zeigt auch den entsprechenden Beschreibungstext aus der Bildquelle. Ist die Differenz null, sind die Werte gleich groß und das Anti-Windup ist nicht aktiv. Stellt sich eine Differenz ein, wird über einen Verstärkerbaustein der Parameter für den I-Anteil um den entsprechenden Wert verringert. Als Faktor wurde der Wert „eins“ gewählt. Für das oben genannte Simulations-Beispiel konnte der Effekt der Anti-Windup-Strategie nachgewiesen werden. Es ist dabei besonders die geringere Totzeit im Plot der Ist-Geschwindigkeit und die schnelle Abnahme des I-Anteils zu beobachten, vgl. Abbildung Anti-Windup: Vergleich Soll- und Istgröße und Reglerparameter.