SDE Systementwurf SoSe2025: Testbericht berechneEntfernungPunktGerade.m

Abb. 1: Berechnung des Abstandes Punkt zu Strecke

Modul:	code>berechneEntfernungPunktGerade.m
Revision:	10780
Autor:	Prof. Dr.-Ing. Schneider
Datum:	25.09.2025
System:	MATLAB®-Funktion
SVN-URL:	https://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/Daten/Rundkurs_L33_E01_210/berechneEntfernungPunktGerade.m

Einleitung

Ziel des Projektes ist eine geregelte Fahrt eines AlphaBot entlang einer definierten Fahrspur (s. SDE_Systementwicklung_WS25/26:_Geregelte_autonome_Fahrt). Die Sollspur liegt als digitale Karte vor und die Istposition wird mit der Robotic Total Station gemessen.

Das zu testende Modul berechneEntfernungPunktGerade.m berechnet die Entfernung des eingehenden Punktes zur Fahrspur.

Tabelle 1: Funktionsübersicht/Zugehörigkeit

#	Datei	Beschreibung
1	berechneEntfernungPunktGerade.m	zu testendes Modul
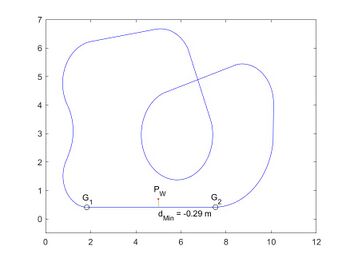
2	testBerechneRegelabweichungSpur.m	Testfunktion für einen Punkt $P_W$ mit Darstellung (vgl. Abb. 1)
3	testBerechneRegelabweichungSpurfcn.m	Testfunktion für die gesamte Fahrspur mit Ergebnisdarstellung (vgl. Abb. 2, 3)
4	RechteFahrspur_W.mat	Eingangsdatum für die rechte Fahrspur
5	LinkeFahrspur_W.mat	Eingangsdatum für die linke Fahrspur
5	[hhttps://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/Daten/Rundkurs_L33_E01_210/MittelLinie_W.mat MittelLinie_W.mat]	Eingangsdatum für die Mittellinie

Funktionaler Systementwurf

Tabelle 2: Funktionale Anforderungen an berechneEntfernungPunktGerade.m

Req.	Beschreibung	Priorität
1	Die Funktion muss die mathematisch kürzeste Strecke $d_{Min}$ des Punktes $P_W$ zur gegebenen Sollinie in m berechnen und als Rückgabe liefern.	1
2	Alle Koordinaten müssen im Welt-Koordinatensystem (Karten-KOS) behandelt werden.	1
3	Die nächstgelegenen Punkte $G_1$ und $G_2$ der Solllinie sollen zusätzlich als kartesische Koordinaten (x, y, z) zurückgegeben werden.	2
4	Fahrtrichtung ist GUZ. Punkte links der Sollinie ist der Wert $d_{Min}$ negativ und rechts positiv.	2

Technische Systementwurf

Abb. 2: PAP zur Bestimmung des min. Abstandes

Der technische Systementwurf wird in Abb. 2 als PAP dargestellt.

Komponentenspezifikation

Die Entfernung des Punktes $P$ von der Strecke $A$ zu $B$ wird mittels Vektorrechnung ermittelt.

1. Berechnung der Ortsvektore: $\overrightarrow{AP}=\overrightarrow{P}-\overrightarrow{A}$, $\overrightarrow{AB}=\overrightarrow{B}-\overrightarrow{A}$
2. Berechne die Projektion von P auf AB (Projektionsfaktor a): $a=\frac{\overrightarrow{AP}\cdot \overrightarrow{AB}}{|\overrightarrow{AB}{|}^2}$
3. Prüfe, ob die Projektion innerhalb des Streckenabschnitts liegt: 0<a<1
4. Berechne die Projektion P' von P auf AB: $\overrightarrow{P^{\prime }}=a\cdot \overrightarrow{AB}$
5. Berechne den Vektor, der senkrecht von P auf AB zeigt: $\overrightarrow{n}=\overrightarrow{AP}-\overrightarrow{P^{\prime }}$
6. Berechne den Abstand als die Länge dieses Vektors: $d=|\overrightarrow{n}|$
7. Vorzeichen gemäß Req. 4 anpassen.

Programmierung

berechneEntfernungPunktGerade.m  Musterlösung: für den Batterie-Tester

function [G1, G2, dMin]= berechneEntfernungPunktGerade(PW,aSollLinie_W)

for i= 1:length(aSollLinie_W)
    if i<length(aSollLinie_W)
        G1 = aSollLinie_W(:,i);
        G2 = aSollLinie_W(:,i+1);
    else
        G1 = aSollLinie_W(:,end);
        G2 = aSollLinie_W(:,1);
    end

    A(:,i)=[G1;0];
    B(:,i)=[G2;0];
    d(i) = berechneEntfernungPunktStrecke(A(:,i), B(:,i), PW);
end
[m index] = min(abs(d)); % geringste Abstand finden

%% Rückgabewerte
dMin = d(index);   % in m
G1   = A(:,index); % in m
G2   = B(:,index); % in m
end


%% -------------------------------------------------------------
function d = berechneEntfernungPunktStrecke(A, B, P)
% -------------------------------------------------------------
% Konvertiere die Input Punkte in Vektoren
AP = P - A;
AB = B - A;

% Berechne die Projektion von AP auf AB (Projektionsfaktor)
projFaktor = dot(AP, AB) / norm(AB)^2;

% Prüfe, ob die Projektion innerhalb des Streckenabschnitts liegt
if projFaktor < 0
    % Punkt P ist näher an A
    d = norm(AP);
elseif projFaktor > 1
    % Punkt P ist näher an B
    BP = P - B;
    d = norm(BP);
else
    % Der projizierte Punkt liegt auf der Strecke AB
    % Berechne die Projektion von AP auf AB
    projAB_AP = projFaktor * AB;
    
    % Berechne den Vektor, der senkrecht von P auf AB zeigt
    perpendicular = AP - projAB_AP;
    
    % Berechne den Abstand als die Länge dieses Vektors
    d = norm(perpendicular);
end

q = A;    % Ortsvektor zum Punkt auf der Geraden
u = B-A;  % Richtungsvektor

% Vorzeichen: in Fahrtrichtung rechts der Sollinie ist positiv
v = cross((P-q),u);
if v(3)<0
    d = -d; % links negativ
end

end

Modultest

Da es sich bei dieser Entwicklung um die einer einzelnen Komponente handelt, schließt der Modultest mit dem Testbericht die Entwicklung ab (vgl. Tabelle 2).

Abb. 3: Ergebnis von Testfall 1

Abb. 4: Ergebnis von Testfall 2

Tabelle 2: Testbericht für den Modultest von berechneEntfernungPunktGerade.m

ID	Testfallbeschreibung	Eingänge PW, Referenz	Erwartetes Ergebnis	Testergebnis	Testperson	Datum
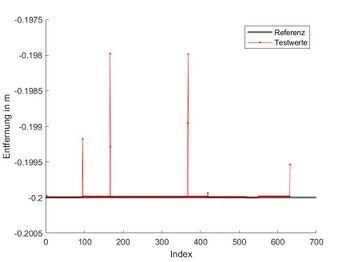
1	Punkte links der Sollinie sind negativ.	[1.83;0.61;0], LinkeFahrspur_W.mat	-0.2 m (vgl. Abb. 3)	OK	Prof. Schneider	19.06.2026
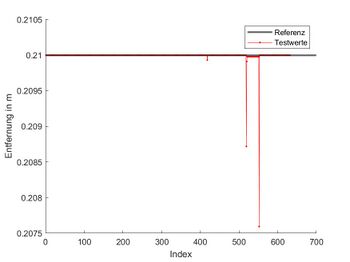
2	Punkte rechts der Sollinie sind positiv.	[1.83;0.2;0], RechteFahrspur_W.mat	0.21 m (vgl. Abb. 4)	OK	Prof. Schneider	19.06.2026

Zusammenfassung

Das Modul berechneEntfernungPunktGerade.m wurde systematisch entworfen, getestet und dokumentiert. Es kann eingesetzt werden, um für eine gemessene Position die Abweichung zur Sollspur zu berechnen. Der AlphaBot kann auf diese Abweichung regeln.

---

→ zurück zum Hauptartikel: SDE Praktikum Systementwurf SoSe2025