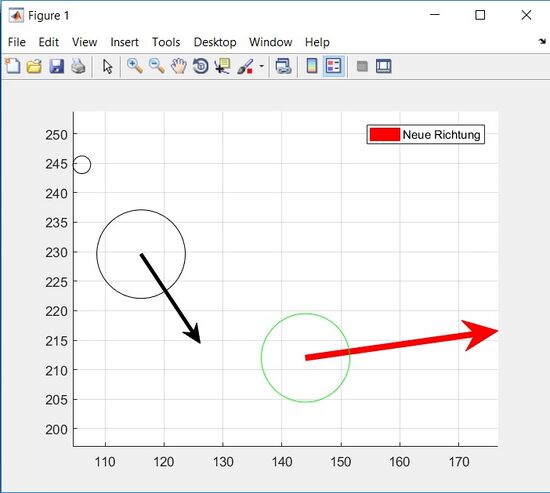
Autoren: Christo Tsibadze, Kevin Penner
Betreuer: Prof. Schneider

Aufgabenstellung

Realisierung einer Billard-Assistenz-Software, mit Hilfe von Matlab und dessen Bildverarbeitungs-Tools: Es soll ein "Billard-Assistenz-Software" entwickelt werden, welche aus einem Video (oder Live-Cam) Billardkugeln- und Queue -Positionen erkennt und anschließend mit einem Algorithmus die Abprallrichtung einer Zielkugel "vorhersagt" (berechnet). Vor dem Schlag soll anhand der Queue- und Kugelpositionen erkannt werden, in welche Richtung die weiße Kugel geschlagen wird. Falls die weiße Kugel eine andere Kugel auf dem Billardtisch trifft, soll im Voraus die Abprallrichtung dieser ermittelt werden. Die berechnete Richtungen soll auf dem Video eingeblendet werden. Für die Bildverarbeitung sowie Programmierung wurde die Matlabversion R2016a verwendet. Eine CAD-Software wurde während der Entwicklung des Algorithmus zur Überprüfung der Ergebnisse eingesetzt.

Erwartungen an die Projektlösung

Sammeln von weiteren Erfahrungen in der Bildverarbeitung mit MATLAB
Umsetzung der in der Vorlesung gewonnenen Erkenntnisse in die Praxis
Tieferer Einblick in die geometrische Physik
Lösen von Problemstellungen durch ingenieurmäßige Herangehensweisen
Erstellung eines benutzerfreundlichen Videos, welches die Software visualisiert

Plannung

Projektplan

Die Gesamtaufgabe wurde wie folgt aufgeteilt:

Kevin Penner:
- Automatische Erkennung von Queue- und Kugelpositionen in einer Videoquelle
- sowie Unterscheidung der Kugeln, weiße- oder Zielkugel

Christo Tsibadze:
- Ein Algorithmus programmieren, der die Schlagrichtung der weißen Kugel berechnet
- Erkennung ob die weiße Kugel nach dem Schlag einen anderen Kugel trifft oder nicht
- Falls die weiße Kugel eine andere Kugel trifft, Berechnung in welcher Richtung die andere Kugel abprallt.

Die Aufgabe ist freiwillig. Zeitlich wurde für das Projekt im 6. Semester je ca. 3 Stunden pro Woche investiert. Zur Ideenfindung oder Besprechung der Problemlösungsstrategien wurde regelmäßiges Wochen-Meeting gehalten.

Erkennung von Queue- und Kugelpositionen

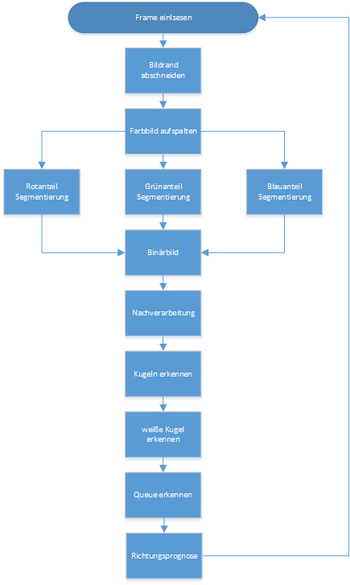
In Abbildung 2 ist ein Ablaufplan zu sehen, welcher den Algorithmus zur Erkennung von Billardkugeln und dem Queue grob veranschaulicht. Im Folgenden wird auf jeden dieser Punkte eingegangen:

Frame einlesen und Zuschneiden des Bildes

Damit das Testen der Algorithmen stattfinden kann, wurden öffentliche Videos von Billardwettkämpfen genutzt. Diese können über die VideoReader Funktion eingelesen werden. Außerdem sind der Anfangsframe (Startframe) und die Schrittweite (Frameschritte) der zu analysierenden Frames einstellbar.

video=VideoReader('001.mp4');
nframes = video.NumberOfFrames;
Frameschritte = 1;
Startframe = 1;

Da die Videos überflüssige Bildbereiche besitzen, wird zunächst der Billardtisch extrahiert, indem ein konstant definierter Bildbereich ausgewählt wird (ROI). Das zu analysierende Bild besitzt nun also einen homogenen Hintergrund (Farbe des Billardtisches), wodurch das Erkennen bzw. Segmentieren der Objekte vereinfacht wird.

Binarisierung

Für die Erkennung der Objekte im Bild (Kugeln und Queue) wird das RGB-Bild in ein Binärbild umgewandelt. Da die Objekte jeweils einen unterschiedlichen Farbwert besitzen, muss für die Binarisierung jeder einzelne Farbkern mit einem Schwellwertverfahren umgewandelt werden. Zur Unterstützung wurde hier das Matlabtool Color Thresholder eingesetzt, welches aus einem vom Benutzer ausgewählten Bildbereiches automatische eine Funktion generiert. Dieser wird im Matlab Code ein RGB-Bild als Parameter übergeben, woraufhin ein Binärbild zurückgegeben wird.
Diese Vorgehensweise muss jedoch für jeden spezifischen Billardtisch durchgeführt werden, falls ein anderer Tisch mit einer anderen Farbe angewendet wird.
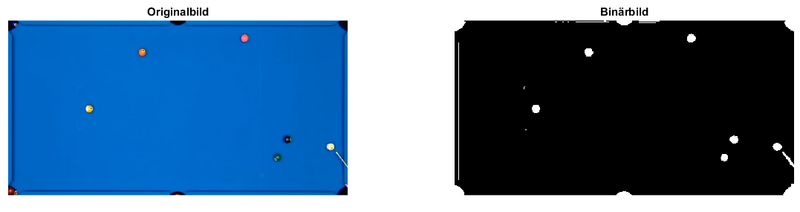
In Abbildung 3 ist die Ausgabe des Originalbildes (links) und des Binärbildes (rechts) zu sehen. An einigen Stellen treten jedoch einzelne Artefakte auf, welche im Nachhinein noch entfernt werden müssen.

Nachverarbeitung

Um später zu Verhindern das Artefakte als Objekte wahrgenommen werden, wird das Binärbild zusätzlich noch bereinigt. Matlab bietet hier eine große Anzahl an Funktionen und morphologischen Operationen an. Folgende zwei Nachverarbeitungsschritte werden durchgeführt:

Schwarze Pixel auf weißen Hintergrund werden gelöscht (Funktion: imfill). Diese Funktion füllt die Löcher in Objekten, damit diese, homogene Flächen besitzen.
Mithilfe der Funktionen imopen und bwareaopen werden kleine weiße Pixelregionen im Bild gelöscht

In Abbildung 4 (rechts) ist nun eine deutliche Veränderung im Gegensatz zu Abbildung 3 (rechts) zu erkennen. Dieses Binärbild kann nun als Grundlage für die Erkennung der Objekte herangezogen werden.

%Binärbild bereinigen
imClean = imfill(BW,'holes');
se = strel('disk',1);
imClean = imopen(imClean,se);
imClean = bwareaopen(imClean, 80);

Kugelerkennung

Für die Erkennung von Kreisen bietet Matlab die Funktion imfindcircles an, welche folgende Parameter übergeben bekommt:

Bereinigtes Binärbild (imClean)
Maximalen und minimalen Radius (in Pixeleinheiten) eines erkannten Kreises
Suche nach hellen Kreisen auf einem dunklen Hintergrund
Kreisformabweichung (wurde experimentell ermittelt)

Als Rückgabewert erhält man eine Liste von Bildkoordinaten der erkannten Kreise und deren Radien.

%Parameter für die Größe und "Genauigkeit" der Billardkugeln
RadiusMin = 6;
RadiusMax = 12;
Circle_Sensitivity = 0.9;

%Kreise im bereinigten Binärbild suchen
[Centers, Radii] = imfindcircles(imClean,[RadiusMin RadiusMax],'ObjectPolarity','bright','Sensitivity',Circle_Sensitivity);
AnzahlKreise = size(Centers);

Erkennung der weißen Kugel

Die Erkennung der weißen Kugel erfolgt über eine selbstgeschriebene Funktion:

function[WhiteCenter, WhiteRadius, WhiteIndex] = Detect_White_Sphere(Centers, Radii, Image)

Dieser werden die Bildkoordinaten und Radien aller erkannten Kreise übergeben, sowie das zugeschnittene RGB-Bild. Als Rückgabewerte erhält man die Koordinaten, den Radius und den Index der weißen Kugel aus dem übergebenen Kreiskoordinatenvektor.
In dieser Funktion werden alle erkannten Kreise in einer Schleife auf deren Helligkeit (vorher muss das RGB-Bild in ein Grauwertbild umwandelt werden) überprüft, indem der Mittelwert über alle Pixelwerte in einem Kreis gebildet wird und so der höchste Wert der weißen Kugel zugeordnet werden kann. Ob sich ein Pixel in einem Kreis befindet, kann mit folgender Formel berechnet werden:

${\displaystyle \mathtt{ PunktInKreis = (x-x_\text{center})^2 + (y-y_\text{center})^2 - r^2 }}$

${\displaystyle \mathtt{ PunktInKreis < 0 \Rightarrow Koordinaten\ liegen\ im\ Kreis }}$

${\displaystyle \mathtt{ PunktInKreis = 0 \Rightarrow Koordinaten\ liegen\ auf\ Kreisbahn }}$

${\displaystyle \mathtt{ PunktInKreis > 0 \Rightarrow Koordinaten\ liegen\ ausserhalb\ des\ Kreises }}$

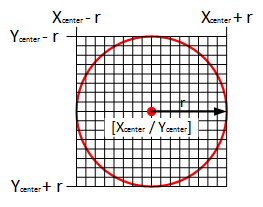
Der Abscannbereich eines jeden Kreises wird wie in Abbildung 5 realisiert, indem ein Quadrat um den Kreis gebildet wird, in welchem anschließend nur die Pixel zum Mittelwert gezählt werden, welche mithilfe der Kreisgleichung zum Kreis zugeordnet werden können.
Der Matlabcode sieht wie folgt aus:

for j=1:AnzahlKreise
   %Boundingbox um Kugel ermitteln
   xmin = round(Centers(j,1)- Radii(j));
   xmax = round(Centers(j,1)+ Radii(j));
   ymin = round(Centers(j,2)- Radii(j));
   ymax = round(Centers(j,2)+ Radii(j));
   %Boundingbox "abscannen". Wenn Punkt im Kreis liegt, dann soll eine
   %Pixelsumme aller Helligkeitswerte gebildet werden. Aus diesen wird
   %dann der Mittelwert gebildet
   PxSum = 0;
   PxInd = 0;
   for m=ymin:ymax
      for n=xmin:xmax
         %PunktinKreis < 0 --> Koordinate liegt im Kreis
         %PunktinKreis = 0 --> Koordinate liegt auf Kreisbahn
         %PunktinKreis > 0 --> Koordinate liegt außerhalb des Kreises
         PunktinKreis = (n-Centers(j,1))^2 + (m-Centers(j,2))^2 - Radii(j)^2;
         if PunktinKreis <= 0 && n <= width && m <= height && n>0 && m>0
            PxSum = PxSum + double(GrayImage(m,n));
            PxInd = PxInd + 1;
         end
      end
   end
   PxMean(j) = PxSum/PxInd;
end

Queueerkennung

Nachdem die weiße Kugel erkannt ist, wird der Queue in der unmittelbaren Umgebung zur weißen Kugel gesucht. Hierzu wurde folgende Funktion implementiert:

[Queue] = Detect_Queue_01(WhiteCenter, DetectionRadius, imClean);

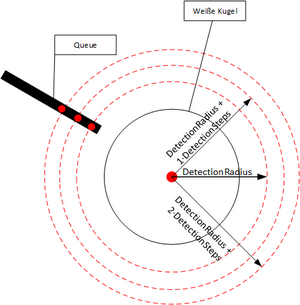
Der Funktion werden die Koordinaten der weißen Kugel, der Absuchradius zur Detektion des Queues und das bereinigte Binärbild übergeben. Als Rückgabewert wird die Position des Queues geliefert.
In der Funktion wird auf der Kreisbahn mit einem Absuchradius um die weiße Kugel nach weißen Pixelwerten gesucht (ob ein Pixel auf der Kreisbahn liegt, wird mit derselben Kreisgleichung, wie bei der Erkennung der weißen Kugel, überprüft). Die Koordinaten der Pixelwerte, die zu dem Queue zugeordnet werden, werden in einen Vektor geschrieben. Um den Mittelpunkt des Queues zu erhalten, wird folgende Berechnung im Anschluss an die Erfassung der Pixelwerte durchgeführt:

${\displaystyle \mathtt{ Queueposition_X = \frac{Min(Queuevektor_X) + Max(Queuevektor_X)}{2} }}$

${\displaystyle \mathtt{ Queueposition_Y = \frac{Min(Queuevektor_Y) + Max(Queuevektor_Y)}{2} }}$

In der Testphase des Algorithmus zur Erkennung hat sich jedoch herausgestellt, dass aufgrund der ungenauen Binarisierung und damit verbundenen schlechten Erkennung des Queues, eine Abweichung zwischen wahrer mittleren Position und erkannter mittleren Position des Queues resultierte. Diese Abweichung konnte durch das Erfassen von mehreren Punkten auf dem Queue minimiert werden (siehe Abbildung 6). Die Funktion wird nun in einer Schleife ausgeführt, in welcher der Absuchradius stetig erhöht wird:

%Absuchradius um weiße Kugel zum detektieren des Queue
DetectionRadius = 15;
DetectionSteps = 5;
Iterationen = 10;

for j=1:Iterationen
   [Queue] = Detect_Queue_01(WhiteCenter, DetectionRadius + (j-1)*DetectionSteps, imClean);
end

Die detektierten Punkte werden in einen Vektor geschrieben. Für das Erhalten eines eindeutigen Punktes auf dem Queue, wird nun noch der Mittelwert aller x- und y-Koordinaten gebildet.

Eingeschränkte Durchführung des Algorithmus

Da die Ermittlung der Queueposition nur erfolgen muss, wenn sich die weiße Kugel im Stillstand befindet, wird vor der Ausführung der Funktion zur Queueerkennung die Positionsveränderung der weißen Kugel kontrolliert. Hierfür wird die Differenz der alten Position der weißen Kugel mit der neuen Position gebildet und mit einem geringem Schwellwert verglichen:

Position_of_rest = ((abs(WhiteCenter(1)-WhiteCenterOld(1))<5) && (abs(WhiteCenter(2)-WhiteCenterOld(2))<5)) 
if Position_of_rest
.
.
.
end

Berechnungen: Schlagrichtung, Aufprallpunkt und Zielrichtung

Nach der Bildverarbeitung jedes Video-Frames wird die Vorhersagefunktion "BILLARD_FINAL_V2" mit folgenden Parametern und Rückgabewerten aufgerufen:

function [ RICHTUNG_Koordinaten, ZIEL_KUGEL, RICHTUNG_Koord_Weiss ] = BILLARD_FINAL_V2( W,Z,Q,R )

W: X- und Y-Koordinaten der weißen Kugel

Format:

[double x;double y]

Z: X- und Y-Koordinaten aller Zielkugeln in einer Matrix

Format:

[[double x1;double y1],[double x2;double y2],...,[double xn;double yn]];

Q: X- und Y-Koordinaten der Queuespitze

Format:

[double x;double y]

R: Kugelradius (Annahme: alle Kugeln sind gleich groß)

Format:

[double r]

Als Rückgabe liefert die Funktion folgende Werte:

RICHTUNG_Koordinaten: ein Vektor mit der Länge von 50 Pixeln, dessen Startpunkt die anvisierte Zielkugel ist und dessen Richtung die vorhersagte Abprallrichtung der Zielkugel beschreibt.

Format:

[double x;double y]

ZIEL_KUGEL: Gibt die Koordinaten der anvisierten Zielkugel zurück

Format:

[double x;double y]

RICHTUNG_Koord_Weiss: Gibt eine Hilfskoordinate zurück, um die "Anvisierlinie" der weißen Kugel zu visualisieren

Format:

[double x;double y]

Falls keine Zielkugel anvisiert wird, werden alle Rückgabewerte mit 0 initialisiert.

Vorbereitung

Da die Y-Achse der Bildkoordinaten bei der Videoverarbeitung von oben nach unten verläuft (positive Y-Werte) und im Vorhersagealgorithmus von unten nach oben (negative Y-Werte), werden alle Y-Koordinaten vor und nach der Berechnung umgekehrt.

%% Y-Achse Umkehren  
Z(2,:) = Z(2,:).*-1;
Q(2) = Q(2).*-1;
W(2) = W(2).*-1;

Sortierung nach Entfernung

Wenn in der Schlagrichtung der weißen Kugel mehrere Zielkugel positioniert sind, ist es erforderlich zu unterscheiden, welche Kugel den kürzesten Abstand zur weißen Kugel besitzt bzw. welche Zielkugel zuerst getroffen wird.

%% Zielkugel mit kleinsten Abstand finden (und sortieren)
Anzahl_Zielkugeln = size(Z,2);
B(3,Anzahl_Zielkugeln)=zeros; %Neue Matrix vorbereiten
B(2,:,:)=Z(1,:); % in die zweite Zeile alle X-Koordinaten der Zielkugeln
B(3,:,:)=Z(2,:); % in die dritte Zeile alle Y-Koordinaten der Zielkugeln
for i = 1: Anzahl_Zielkugeln
    B(1,i,:) = norm(Z(:,i)-W); % in die erste Zeile --> Abstände aller Zielkugeln zur weißen Kugel 
end
B = sortrows(B')'; % Matrix transponieren, nach Abstände zur weißen Kugel ordnen und zurücktransponieren

Die Anzahl der Spalten ist gleich der erkannten bzw. übrig gebliebenen Zielkugeln. Für die Sortierung nach der Entfernung wird eine neue Matrix B mit drei Zeilen erzeugt. Die X- und Y-Koordinaten aus der Z-Matrix werden in die zweite und dritte Zeile der B-Matrix eingetragen (1. --> 2 und 2. --> 3.). In der ersten Zeile wird für jede Zielkugel die Entfernung zur weißen Kugel berechnet und eingetragen.

Die Entfernung einer Zielkugel zur weißen Kugel wird wie folgt ermittelt:

Vektorbestimmung anhand der Koordinaten von Ziel- und weißer Kugel
```
[x1-x1;y1-y2]
```
Entfernung: Länge des Vektors bestimmten
```
sqrt(x^2 + y^2)
```

Nachdem alle Entfernungen der Zielkugeln in die erste Zeile der B-Matrix eingetragen wurden, wird mithilfe der MATLAB-Funktion sortrows die Matrix aufsteigend (nach Entfernungen) sortiert.

Da die Funktion

sortrows

den Inhalt der ersten Matrizenspalte aufsteigend ordnet, jedoch die Entfernungen in unserem Fall in der ersten Zeile stehen, wird die Matrix vor und nach dem Sortieren transponiert. Beim Transponieren werden die Zeilen und Spalten vertauscht bzw. Zeilen in Spalten und Spalten in Zeilen umgewandelt.

Nach der Sortierung besteht die B-Matrix aus drei Zeilen:

1. Zeile: Abstände zur weißen Kugel (aufsteigend geordnet)
2. Zeile: X-Koordinaten der Zielkugeln
3. Zeile: Y-Koordinaten der Zielkugeln

Die Spaltenanzahl entspricht der Anzahl der Zielkugeln.

Schlagrichtung weiße Kugel

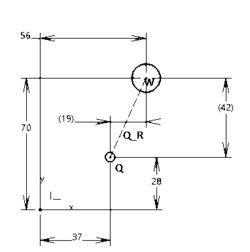
Um herauszufinden in welche Richtung die weiße Kugel geschlagen bzw. anvisiert wird, wird mithilfe der Koordinaten des Queues Q(x;y) und der weißen Kugel W(x;y), ein Schlagrichtungsvektor berechnet und anschließend normiert.

%% Richtung Direkt
Q_R=(W-Q);% Richtung QW Queue-Weiss
Q_R_Norm = Q_R./norm(Q_R); %Vektor normieren

Die Vektornormierung wird wie folgt berechnet: Der Vektor wird durch seine eigene Länge geteilt. Einfachheitshalber wird angenommen das mit der Queuespitze immer auf die Mitte der weißen Kugel gezielt wird, da das Projekt sonst im verfügbaren Zeitrahmen nicht machbar gewesen wäre.

Treffer oder kein Treffer

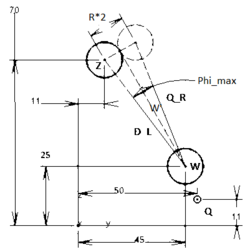
Um herauszufinden, ob die weiße Kugel in der Schlagrichtung einen Zielkugel trifft, werden folgende Berechnungen durchgeführt:
Es wird ein imaginäres gleichschenkliges Dreieck aufgestellt mit folgenden gegebenen Seitenlängen (siehe Abbildung 7):

Länge der kleinen Seite: 2 x Kugelradius (bzw. 1 x Kugeldurchmesser)
Länge der langen Seite: Entfernung der weißen Kugel zur Zielkugel (Direkte Linie: D_L)

Als Länge der kleinen Seite wurde der Kugeldurchmesser gewählt, da sich die Kugeln bei einem Kontakt berühren. Zu bestimmen ist der Winkel "Phi_max" (siehe Abbildung 7). Dieser Winkel ist zwischen der Schlagrichtung der weißen Kugel Q_R und der direkten Richtung D_L eingeschlossen und ist abhängig von der Entfernung der Zielkugel zur weißen Kugel. Die Zielkugel kann nur dann getroffen werden, wenn der aktuelle Winkel (Alpha) kleiner ist als Phi_max.

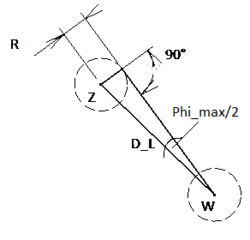
Für die Bestimmung von Phi_max von jeder Zielkugel wird zunächst nur die Hälfte des gleichschenkligen Dreiecks betrachtet --> rechtwinkliges Dreieck (siehe Abbildung 8)

D_L: Direkte Linie zwischen der Ziel- und weißen Kugel entspricht der Hypotenuse
- Anfangsposition der D_L: Koordinaten der weißen Kugel
- Endposition der D_L : Koordinaten der Zielkugel
- Länge der D_L: Betrag des Vektor, welcher zwischen Ziel- und weißer Kugel aufgespannt wird
Länge der Gegenkathete: Kugelradius
Winkel zwischen Gegen- und Ankathete: 90°

Da die Hypotenuse, die Gegenkathete und ein Winkel bekannt sind, ist der gesuchte Winkel mithilfe des Sinus ermittelbar:
--> Phi_max = 2 * arcsin(Gegenkathete/Hypotenuse)

Phi_max=2*asind((R)/B(1,i,:)); %maximaler Winkel für Treffer

Anschließend wird der aktuelle Winkel "Alpha" zwischen den D_L- und Q_R Vektoren wie folgt berechnet:

Winkel zwischen Vektoren Skalarprodukt

D_L=(B(2:3,i,:)-W);% direkte Richtung, zwischen Ziel- und weißer Kugel
%% aktueller Winkel Schlagrichtung bzw. direkte Richtung
Alpha = acosd((dot(Q_R,D_L))/((norm(Q_R) * norm(D_L)))); % Winkel zwischen Q_R und D_L

Ist der Winkel Alpha kleiner als Phi_max --> Treffer, sonst kein Treffer.

Falls Treffer: Abprallrichtung

Mithilfe des Algorithmus wird zuerst geprüft, ob die Zielkugel mit dem kleinstem Abstand zur weißen Kugel in aktueller Queuerichtung getroffen wird. Falls dies nicht der Fall ist, wird die Zielkugel mit dem nächst kleineren Abstand geprüft, bis eine Zielkugel gefunden wird, die getroffen wird. Ist eine Zielkugel gefunden, die getroffen wird, wird die Abprallrichtung der Zielkugel berechnet.

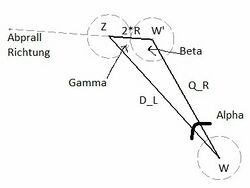
Gegeben ist ein allgemeines Dreieck mit:

D_L: die Direkte Linie zwischen den weißen- und ziel Kugel
- Länge, Richtung und Position
Q_R: die Schlagrichtung der weißen Kugel
- Startpunkt (weiße Kugel), Richtung, keine Länge
Alpha: Winkel Alpha ist ermittelbar durch zwei Vektoren ( D_L & Q_R)
2*R: Richtung zwischen den Zielkugel und den weißen Kugel beim aufprall
- Länge = 2 mal Kugelradius, ein fester Punkt bei Zielkugel

Gesucht: Der Winkel Beta und Position von Überschneidungspunkt W' , sowie der Winkel im Punkt Z --> Gama

Trigonometrisch gesehen sind Zwei lange Seiten des Dreiecks bekannt und der Winkel zwischen diesen Seiten. Also ist es möglich mit Hilfe des Kosinus-Satzes die restlichen Parameter herauszurechnen.
Siehe folgende Quelle: Berechnung eines beliebigen Dreiecks

    Beta=180-asind((B(1,j,:)/(2*R))*sind(Alpha)); %
    Gama=180-Beta-Alpha;

Sind alle Winkeln bekannt, dann ist mit dem Winkel Gama möglich die Kugelabprallrichtung zu bestimmen. Denn genau um diesen Winkel muss der Vektor D_L rotiert werden um den Kugelabprallrichtung zu bekommen.

Die Rotation einer Linie bzw. Vektor ist mit Multiplikation dessen mit einem Rotationsmatrix möglich.

Fallunterscheidungen

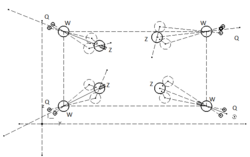
Um die korrekte Abprallrichtung der Zielkugel zu berechnen ist es notwendig, verschiedene Fälle zu unterscheiden.
Wird der Zielkugel von:

links nach rechts
rechts nach links
oben nach unten
unten nach oben geschlagen?... dann... Siehe Matlab Ausschnitt

    %% Fallunterscheidung für Winkel Gama, Anordnung W und Z
    if((W(1)<B(2,j,:))&&(W(2)>B(3,j,:)))
        Fall = 1; %Schlag von links oben
    end
    if((W(1)<B(2,j,:))&&(W(2)<B(3,j,:)))
        Fall = 2; %Schlag von links unten
    end
    if((W(1)>B(2,j,:))&&(W(2)>B(3,j,:)))
        Fall = 3; %Schlag von rechts oben
        Gama=(180-Gama);
    end
    if((W(1)>B(2,j,:))&&(W(2)<B(3,j,:)))
        Fall = 4; %Schlag von rechts unten
        Gama=(180-Gama);
    end

...und Treffer auf linke oder rechte Hälfte der Zielkugel...

    %% Winkelberechnung für Orientierung im 2D-Raum
    Winkel_1 = acosd((dot(RefH,Q_R))/((norm(RefH) * norm(Q_R))));
    Winkel_2 = acosd((dot(RefH,D_L))/((norm(RefH) * norm(D_L))));
    if(Winkel_1 == Winkel_2)
            Gama=0;
    else
        switch Fall
            case 1
                if(Winkel_1 > Winkel_2)
                    Gama=-Gama;
                end
            case 2
                if(Winkel_1 < Winkel_2)
                    Gama=-Gama;
                end
            case 3
                if(Winkel_1 < Winkel_2)
                    Gama=-Gama;
                end
            case 4
                if(Winkel_1 > Winkel_2)
                    Gama=-Gama;
                end
        end
    end

Je nach Kugel-Anordnung wird im Rotationsmatrix entweder negative- oder positive Gama, oder 180°-Gama eingegeben.

Für die Ermittlung der richtigen Abprallrichtung waren es mehrere Rotationen um 90° und Vektorumkehrungen mit Multiplikation mit -1 notwendig. Um den Überblick nicht zu verlieren wurden selbst erstellte CAD-Skizzen und MATLAB-GUI zuhilfe genommen. Somit wurden alle Fälle geprüft und die Software angepasst bzw. debuggt.

    %% Rotation von D_L auf Abprallrichtung
    RICHTUNG_NEU=rot90(W-B(2:3,j,:))*[cosd(Gama) -sind(Gama); sind(Gama) cosd(Gama)];
    RICHTUNG_NEU=rot90(rot90(rot90((RICHTUNG_NEU)))).*-1;
    if(Fall==4 || Fall==3)
        RICHTUNG_NEU=RICHTUNG_NEU.*-1;1
    end;

Rückgabewerte

if(Q(1)~= 0 && Q(2) ~= 0) % Rückgabewerte nur wenn Queueposition bekannt ist
        RICHTUNG_NEU = RICHTUNG_NEU./norm(RICHTUNG_NEU); %normieren
        RICHTUNG_NEU = RICHTUNG_NEU.*50; %feste Vektorlänge von 50 Pixel
        RICHTUNG_Koordinaten(1) = B(2,j,:)+RICHTUNG_NEU(1); % X-Komponente der Rückgabevektor für Abprallrichtung mit Startpunkt (Zielkugel)
        RICHTUNG_Koordinaten(2) =  B(3,j,:).*-1+RICHTUNG_NEU(2).*-1; % Y-Komponente der Rückgabevektor für Abprallrichtung mit Startpunkt (Zielkugel), Richtung angepasst
        ZIEL_KUGEL = [B(2,j,:) ; B(3,j,:).*-1]; % Koordinaten der aktuell anvisierten Zielkugel, Y-Koodrinate angepasst
        RICHTUNG_Koord_Weiss = B(1,j,:).*Q_R_Norm+W; % Hilfslinie Startpunkt Weiße Linie X-Komponente
        RICHTUNG_Koord_Weiss(2) = RICHTUNG_Koord_Weiss(2).*(-1);% Hilfslinie Startpunkt Weiße Linie Y-Komponente angepasst
end

Die Rückgabewerte werden so angepasst dass die Y-Komponenten wieder in die richtige Richtung zeigen für die Bildverarbeitung.

MATLAB GUI

Für die TEST_Versuche wurde eine MATLAB GUI erstellt womit jede mögliche Szenario (Kugelanordnung und Schlagrichtung) Simulierbar ist. Mit Hilfe dessen wurde die Software optimiert und von diversen kleineren Fehlern befreit.

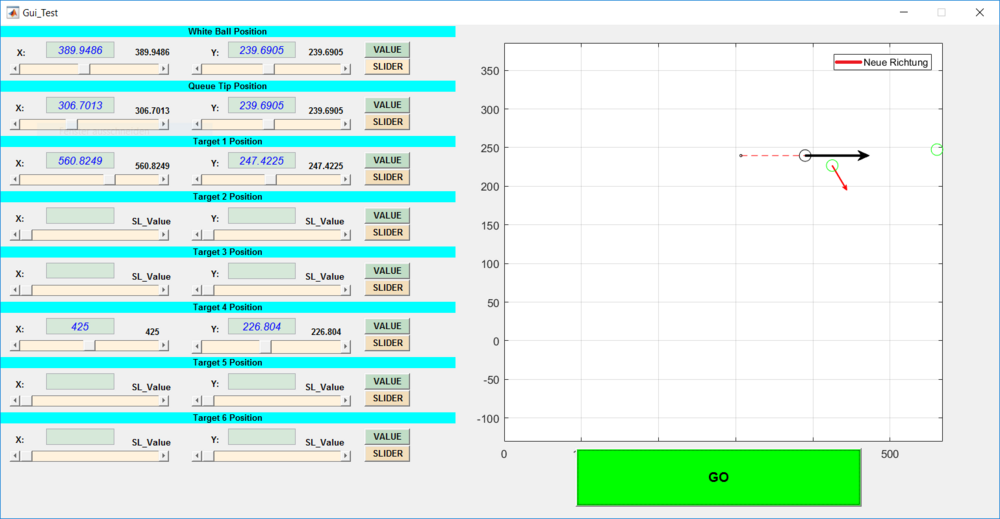
Die einzelne Positionen werden entweder per Slider oder manuell eingegeben. Wird auf die "GO"-Taste gedrückt, dann berechnet die Software die Abprallrichtung und gibt diese als Darstellung aus.

Ausgabe/Resultat

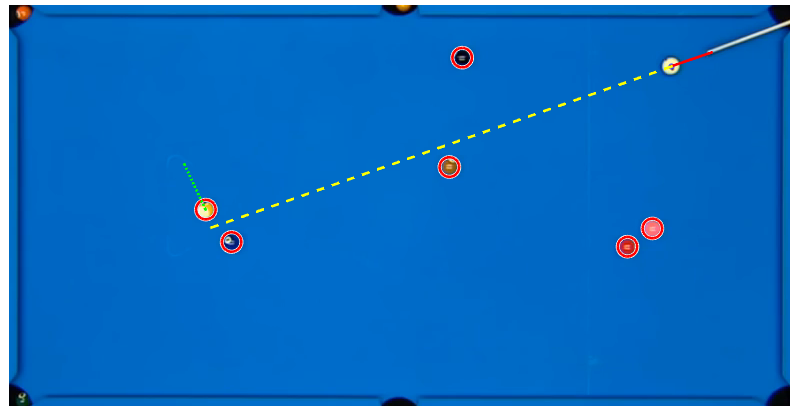
Als Ausgabe erfolgt die Darstellung des zugeschnittenen Originalbildes (siehe Abbildung 12) inklusive folgender Geraden, Punkte und Kreise:

Gerade zwischen Queueposition und des Mittelpunktes der weißen Linie (rote Linie)
Gerade zwischen Mittelpunkt der weißen Kugel und Aufprallpunkt an der Zielkugel (grüne Linie)
Gerade zwischen Mittelpunkt der Zielkugel und Richtung der Zielkugel (gelbe Linie)
Mittelpunkt der weißen Kugel (blauer Punkt)
Umrandung aller Kugeln auf dem Billardtisch (rote Kreise)

Dokumentation

Video

Hier wird ein Link zum Youtube bereitstehen wenn das Video fertig ist.

Fazit

Die von uns angestrebte Ziele wurden erreicht! Die Bildverarbeitung sowie das anspruchsvolle Billardalgorithmus haben uns mit vielen nützlichen Erfahrungen bereichert und auch sehr viel Spaß gemacht. Mit mehr zeitlichen Ressource wären in diesem Projekt weitere Ziele denkbar:

Eingelocht oder nicht
Kugelabprall an den Banden
Berechnung ob die getroffene Kugel weiteren Kugeln trifft und ob diese nochmals weitere Kugeln treffen und dessen Richtungen visualisieren...

Ende gut, alles gut :)

→ zurück zum Hauptartikel: DSB SoSe2016

Pool-Billard Assistenz

Inhaltsverzeichnis

Aufgabenstellung

Erwartungen an die Projektlösung

Plannung

Projektplan

Erkennung von Queue- und Kugelpositionen

Frame einlesen und Zuschneiden des Bildes

Binarisierung

Nachverarbeitung

Kugelerkennung

Erkennung der weißen Kugel

Queueerkennung

Eingeschränkte Durchführung des Algorithmus

Berechnungen: Schlagrichtung, Aufprallpunkt und Zielrichtung

Vorbereitung

Sortierung nach Entfernung

Schlagrichtung weiße Kugel

Treffer oder kein Treffer

Falls Treffer: Abprallrichtung

Fallunterscheidungen

Rückgabewerte

MATLAB GUI

Ausgabe/Resultat

Dokumentation

Video

Fazit

Navigationsmenü