Temperaturregelung des Scheinwerfers Godox SL60W: Unterschied zwischen den Versionen
| Zeile 120: | Zeile 120: | ||
|} | |} | ||
Abschließend erfolgt ein Test der Schaltung. Dazu wird diese auf einem Steckbrett aufgebaut, die Spannung | Abschließend erfolgt ein Test der Schaltung. Dazu wird diese auf einem Steckbrett aufgebaut, die Spannung <math>U_{ADU}</math> von einem analogen Eingang des Arduino Nano ausgelesen und der berechnete Temperaturwert über einen seriellen Monitor ausgegeben. Der Vergleich mit der auf dem Display des Scheinwerfers angezeigten Temperatur bestätigt den Einsatz dieser Messschaltung. | ||
=== Kennwerte des Sensors === | === Kennwerte des Sensors === | ||
Version vom 15. November 2022, 22:10 Uhr
Autor: Daniel Gosedopp
Betreuer: Prof. Göbel
Aufgabenstellung
Die COVID-19 Pandemie hat weitreichende Folgen, auch in der Lehre, mit sich gebracht. Vorlesungen konnten nicht mehr in den Hörsälen der Universitäten und Fachhochschulen stattfinden, sondern mussten auf digitalem Wege durchgeführt werden. Daher spielt das Thema "digitale Lehre" weiterhin eine Rolle im Hochschulalltag. Im Studiengang Mechatronik an der HSHL wird in einigen Vorlesungen auf das invertierte Klassenzimmer gesetzt. Dies ist ein Konzept, bei dem sich Studierende die Vorlesungen im Vorfeld per Video anschauen und den gelernten Inhalt dann im Hörsaal diskutieren und vertiefen. Um in den Videoaufnahmen für ausreichende Beleuchtung zu sorgen, kommen z.B. LED-Scheinwerfer zum Einsatz. Im Betrieb wird von den LED-Panels Wärme erzeugt, die abgeführt werden muss, um den Scheinwerfer nicht zu beschädigen und damit langlebiger zu machen. Dieses Projekt beschäftigt sich mit dem Godox SL60W Scheinwerfer, welcher die Wärme über einen Kühlkörper mit darauf montiertem Lüfter abführt. Der verbaute Lüfter wird allerdings nicht geregelt, sondern nur in Abhängigkeit von der mit einem Drehpotentiometer eingestellten Helligkeitsstufe mit konstanter Drehzahl gesteuert. Dies sorgt für Lärm, welcher bei den Aufnahmen stören kann. Um den Lärm möglichst gering zu halten, soll der Lüfter in Abhängigkeit von der aktuellen, gemessenen Temperatur am Scheinwerfer geregelt werden. Die Regelung wird von einem Mikrocontroller (kurz: µC) übernommen, der zunächst ausgewählt werden muss. Anschließend sind Schaltungen zum Auslesen des Temperatursensors und zum Ansteuern des Lüfters zu entwerfen, testen und integrieren. Danach wird ein Modell des Systems in MATLAB/Simulink gebildet, um den Regler auszulegen und am realen System zu testen.
Entwicklung der Elektronik
Dieser Teil beinhaltet die Entwicklung von Schaltungen zum Messen der Temperatur sowie zur Ansteuerung des Lüfters. Dazu wird ein µC benötigt, welcher vorab ausgewählt werden muss.
Wahl eines Mikrocontrollers
Im Studium und Privatgebrauch werden häufig Arduino-Boards genutzt, da diese einfach zu bedienen sind und viel Wissen in z.B. Internetforen erfragt oder geteilt werden kann. Außerdem lassen sich Arduinos mit MATLAB/Simulink programmieren, sodass in der Simulation getestete Software direkt auf den µC geladen werden kann. Der Arduino Nano besitzt einen 10 Bit Analog-Digital-Umsetzer (kurz: ADU), um das Sensorsignal auszulesen, sowie die Möglichkeit, ein pulsweitenmoduliertes (kurz: PWM) Signal zur Ansteuerung des Lüfters zu erzeugen. Darüberhinaus nimmt der Nano wenig Bauraum in Anspruch und ist preisgünstig. Daher wird für dieses Projekt ein Arduino Nano (siehe Abbildung 1) als µC verwendet.
-
Abbildung 1: Arduino Nano. [1]
Wahl eines Temperatursensors
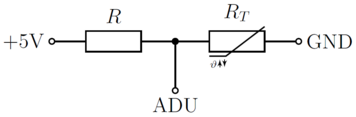
Um den Lüfter in Abhängigkeit der Temperatur zu regeln, ist ein Sensor zur Erfassung der Temperatur nötig. Am Scheinwerfer ist bereits ein Sensor im Kühlkörper des LED-Panels verbaut, welcher zunächst für erste Messungen genutzt wird. Die Auswerteschaltung des Temperatursensors auf der am Scheinwerfer verbauten Platine ist ein Spannungsteiler, der vom Pin des Mikrocontrollers versorgt wird. Die abfallende Spannung über den Temperatursensor wird dabei nach Abbildung 2 vom Mikrocontroller über den ADU ausgelesen. Bei handelt es sich um einen Widerstand.
-
Abbildung 2: Sensorschaltung der Platine des Scheinwerfers.
Da der Temperatursensor keine Beschriftung besitzt und damit keine direkte Identifizierung des Messverhaltens möglich ist, werden Messungen zur Bestimmung der Sensorart durchgeführt. Dazu wird zunächst der Widerstand des Sensors bei einer Umgebungstemperatur von ungefähr mit einem Multimeter gemessen. Dieser lag bei und lässt einen Nennwiderstand des Sensors von vermuten. Weitere Messungen bei verschiedenen Temperaturen und mit Abgleich der im Display des Scheinwerfers angegebenen Temperaturen bestätigen die Vermutung und ergeben außerdem, dass es sich um einen Temperatursensor mit negativem Temperaturkoeffizient (engl. Negative Temperature Coefficent, kurz: NTC) handelt. Das bedeutet, dass der Widerstand mit steigender Temperatur sinkt. Die Messkette zeigt Abbildung 3.
-
Abbildung 3: Messkette des Temperatursensors.
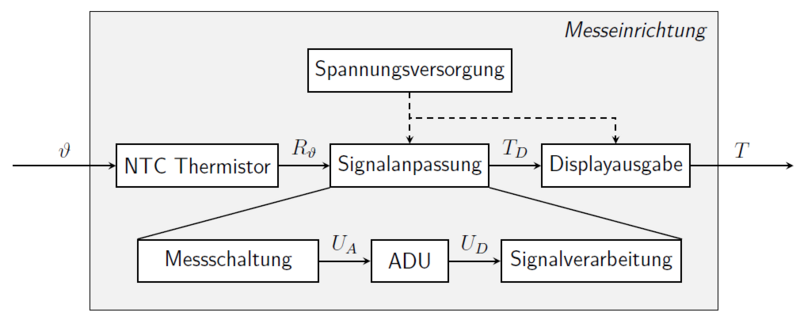
Der NTC-Widerstand ist der Elementarsensor, welcher aus der physikalischen Größe "Temperatur" () einen bestimmten elektrisch auswertbaren Widerstand erzeugt. Um den Widerstand mit einem µC auswerten zu können, wird eine Messschaltung genutzt. Diese erzeugt eine zum Widerstand proportionale analoge Spannung , die wiederum vom ADU des Mikrocontrollers digitalisiert wird (). Auf dem Mikrocontroller findet die digitale Signalverarbeitung statt. Hier wird die digitale Spannung wieder in einen Widerstandswert umgerechnet, aus dem mittels Kennlinie der digitale Temperaturwert berechnet und auf dem Display als Messwert ausgegeben wird.
Erst im späteren Verlauf der Projektbearbeitung wurde deutlich, dass der Lüfter von einem separaten Netzteil versorgt werden muss und der verbaute Sensor nicht genutzt werden kann. Das heißt, dass die Vorarbeiten allesamt mit dem bereits verbauten Sensor getätigt wurden. Aus diesem Grund wird ein baugleicher Sensor für die Regelung gewählt, welcher folgend charakterisiert wird.
Kennlinie des Sensors
Für NTC-Widerstände lässt sich die Kennlinie mit der Steinhart-Hart Gleichung beschreiben:
Fehler beim Parsen (Unbekannte Funktion „\label“): {\displaystyle \frac{1}{{\vartheta}} = A + B\cdot \log(R_{\vartheta}) + C\cdot \log(R_{\vartheta})^{3}. \label{eq_Steinhart1} }
Dabei ist der Widerstand des Sensors bei der Temperatur in Kelvin. Die unbekannten Koeffizienten , und müssen durch Lösen eines linearen Gleichungssystems (kurz: LGS) mit drei Gleichungen berechnet werden. In Matrix-Vektor-Form ergibt sich das LGS
Für die drei Gleichungen sind zuvor Widerstands-Temperatur-Paare aufzunehmen. Als Temperaturreferenz dient die auf dem Display des Scheinwerfers angezeigte Temperatur. Die Widerstandswerte des NTC werden mit einem Multimeter gemessen. Da das Display die Temperatur nur als Ganzzahl ausgibt, variiert der Widerstand bei einer angezeigten Temperatur innerhalb eines Fensters. Hier wird jeweils der Mittelwert dieses Widerstandsfensters der zugehörigen Temperatur zugeordnet. Die Ergebnisse zeigt Tabelle 1.
| Temperatur | 25 | 35 | 45 |
| Widerstand | 10,475 | 6,865 | 4,575 |
Durch Lösung des LGS aus \gleichung{eq_Steinhart2} ergibt sich mit diesen Wertepaaren der Koeffizientenvektor
Die Kennlinie des Sensors kann mit dem Kehrwert der Steinhart-Hart Gleichung beschrieben werden:
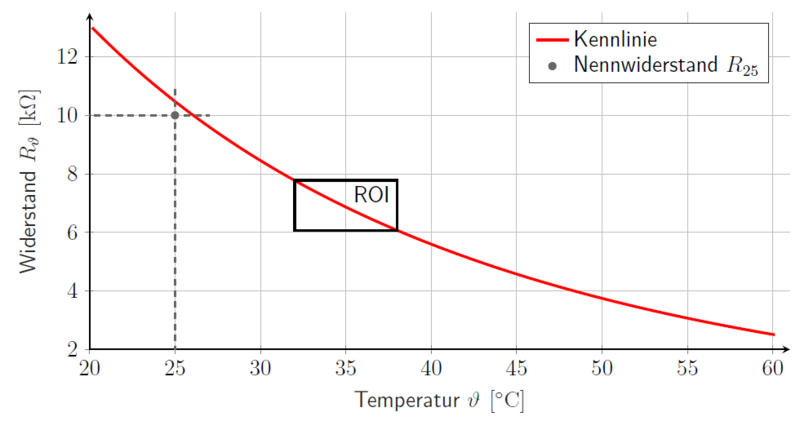
Abbildung 4 stellt diese nach Umrechnung der Temperatur von in dar. Der graue Punkt zeigt den Nennwiderstand des (idealen) NTC-Thermistors. Es ist erkennbar, dass die Kennlinie nicht durch diesen Punkt verläuft. Dies ist auf Fertigungstoleranzen, Messfehler und eine evtl. nicht korrekte Temperaturberechnung im Chip des Scheinwerfers, welche als Referenz dient, zurückzuführen. Der Verlauf dieser Kennlinie wird später zur Ermittlung der Regelstrecke verwendet.
-
Abbildung 4: Kennlinie des Temperatursensors.
Da für dieses Projekt nur ein bestimmter Temperaturbereich von Bedeutung ist, kann ein Gebiet von Interesse (engl. Region Of Interest, kurz: ROI) festgelegt werden (schwarzes Rechteck). Zu einem späteren Zeitpunkt wird erläutert, wie es zu dieser ROI kommt. Für den Bereich von bis werden dann erneut Widerstandsfenster aufgenommen, um die Kennlinie hier möglichst exakt abzubilden. Dies zeigt Abbildung 5.
-
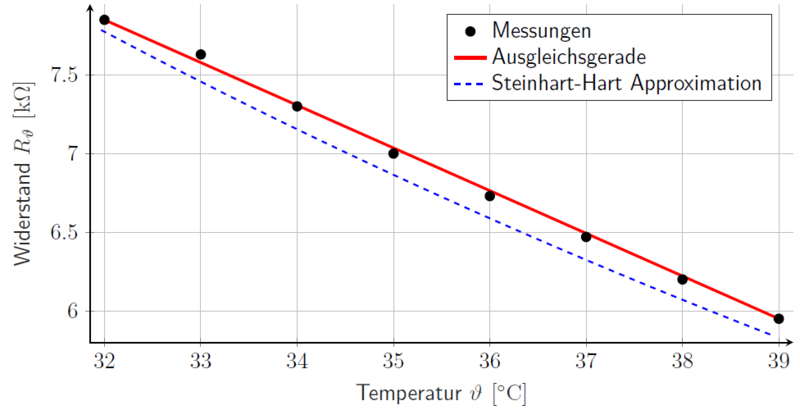
Abbildung 5: Kennlinie des Temperatursensors in der ROI.
Hier ist auch der Verlauf nach der Steinhart-Hart Approximation dargestellt, wobei die Abweichung von den realen Messwerten ersichtlich wird. Das annähernd lineare Verhalten der Messpunkte wird durch eine Ausgleichsgerade verdeutlicht.
Auslegung von Messschaltungen
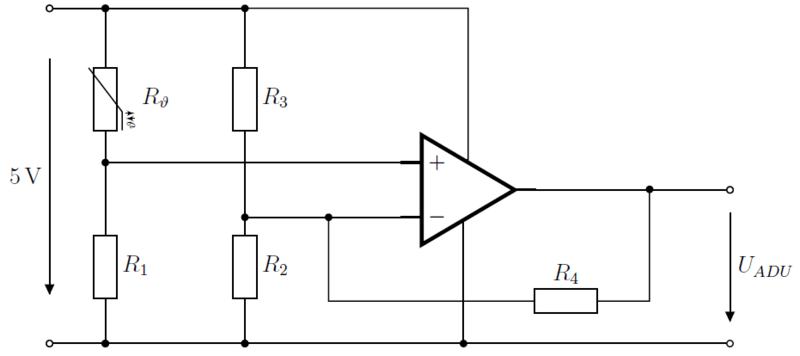
Im Rahmen dieses Projekts werden zwei unterschiedliche Messschaltungen zur Bestimmung der Regelstrecke und für die eigentliche Regelung verwendet. Da zur Aufnahme der Regelstrecke ein relativ großer Temperaturbereich auswertbar gemacht werden muss, wird hierzu der gleiche Spannungsteiler wie in Abbildung 2 genutzt. Die Regelung besitzt höhere Anforderungen an die Auflösung, weshalb eine Verstärkerschaltung mit Offset ausgelegt wird (siehe Abbildung 6).
-
Abbildung 6: Messchaltung des NTC.
Ziel der Schaltung ist es, die abfallende Spannung am Widerstand im Bereich der ROI auf bis zu verstärken, um die Temperatur präziser zu berechnen. Da die Kennlinie hier annähernd linear verläuft, wird der Verlauf der Ausgangsspannung zur Temperatur ebenfalls als linear angenommen. Unter diesem Link findet sich eine Schritt-für-Schritt Anleitung zur Berechnung der Widerstandswerte, an der sich orientiert wird. Hier ist außerdem geschildert, dass der Operationsverstärker (kurz: OPV) die Eigenschaft "Rail-to-Rail" besitzen muss. Damit wird sichergestellt, dass die Ausgangsspannung die Grenzen der Betriebsspannungen des OPVs erreichen kann. Ein MCP6002 besitzt diese Eigenschaft und wird deshalb verwendet. Zur Dimensionierung der Widerstände genügen die Versorgungsspannung der Schaltung sowie die gewünschten Ausgangsspannungen bei Minimal- und Maximaltemperatur der ROI. Die Ergebnisse zeigt Tabelle 2.
| Widerstand | ||||
| Wert |
Abschließend erfolgt ein Test der Schaltung. Dazu wird diese auf einem Steckbrett aufgebaut, die Spannung von einem analogen Eingang des Arduino Nano ausgelesen und der berechnete Temperaturwert über einen seriellen Monitor ausgegeben. Der Vergleich mit der auf dem Display des Scheinwerfers angezeigten Temperatur bestätigt den Einsatz dieser Messschaltung.
Kennwerte des Sensors
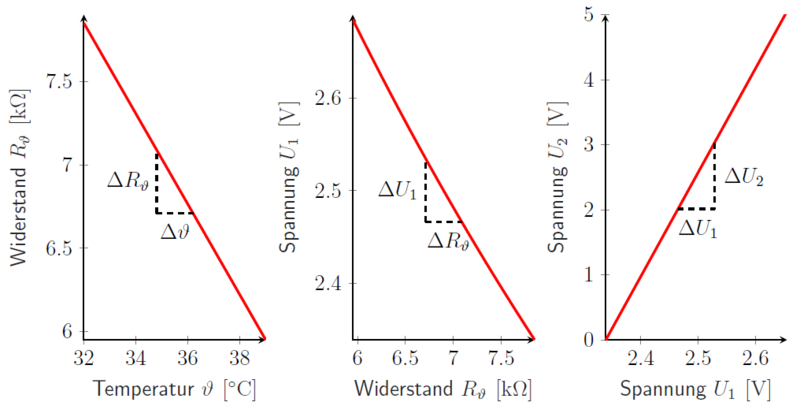
Die Empfindlichkeit des Sensors in der ROI entspricht der Steigung der Ausgleichsgeraden aus Abbildung 5, welche sich zu
berechnet. Für diesen Anwendungsfall ist aber die Gesamtempfindlichkeit der Messschaltung aussagekräftiger, weshalb diese im Folgenden Schritt für Schritt berechnet wird. Die Messschaltung besteht aus den Kernelementen Elementarsensor, Spannungsteiler und Messverstärker. Aus den Kennlinien lässt sich mit Steigungsdreiecken die jeweilige Empfindlichkeit berechnen. Die Kennlinie des Elementarsensors wurde bereits behandelt. Die des Spannungsteilers ergibt sich aus der Spannungsteilerregel:
ist die Spannung, die am Widerstand abfällt. Diese Spannung liegt auch am nicht-invertierenden Eingang des OPVs an. Mit den Werten aus Tabelle 2 und Abbildung 6 ergibt sich ein annähernd linearer Verlauf in der ROI. Die Kennlinie des Messverstärkers errechnet sich zu
Dabei ist die Ausgangsspannung des OPV, die Konstante der Offset, also die Spannung bei einer Temperatur von und der Verstärkungsfaktor des OPVs. Letzterer hat bei vorliegender Beschaltung einen Wert von ca. . Die jeweiligen Kennlinien der Elemente sind zusammen mit den Steigungsdreiecken in Abbildung 7 abgebildet.
-
Abbildung 7: Kennlinien und Empfindlichkeitsdreiecke der Messglieder.
Für die weiteren Empfindlichkeiten ergeben sich demnach
und
Die Gesamtempfindlichkeit in der ROI errechnet sich zu
Eine weitere Kenngröße ist die Auflösung. Der ADU des Arduino Nano besitzt eine Auflösung von , sodass Werte digital abgebildet werden können. Für eine Quantisierungsstufe ergibt sich ein Wert von
In ausgedrückt ergibt sich mit der Gesamtempfindlichkeit eine theoretische Auflösung von
Da es sich beim Scheinwerfer bzgl. der Erwärmung um ein träges System handelt, bei dem im Messsignal keine hohen Frequenzen zu erwarten sind, wird die Abtastrate nicht explizit beachtet, sondern von der Dauer eines Programmzyklus bestimmt. Das Signal wird so mehr als zehn Mal pro Sekunde abgetastet, was zur präzisen Regelung ausreicht. Zur Filterung des Messsignals wird auf Basis von Probemessungen ein Tiefpassfilter nach der Gleichung
mit gewählt. Dadurch wird das Messrauschen weitestgehend eliminiert. Hier ist der neue Schätzwert, der alte Schätzwert, der aktuelle Messwert und eine Gewichtungskonstante im Bereich . Je geringer der Wert von ist, desto höher wird der aktuelle Messwert gewichtet.
Ansteuerung des Lüfters
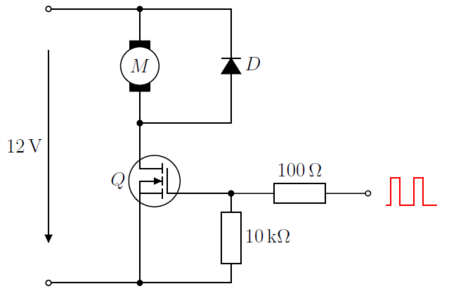
Da das Netzteil des Scheinwerfers keine konstanten für den Lüfter liefert, sondern abhängig von der eingestellten Helligkeitsstufe des LED-Panels eine rein analoge Spannung von bis , kann dieses zur Ansteuerung nicht genutzt werden. Die Ansteuerung mittels eines PWM-Signals, welches vom Mikrocontroller ausgesendet wird, ist nur bei konstanter Versorgungsspannung beherrschbar. Das LED-Panel wird mit einer Spannung von bis versorgt. Zuerst wird überprüft, ob diese Spannung genutzt werden kann, um einen Spannungsregler zu betreiben. Der LM7812 Chip kann eine Eingangsspannung von bis auf eine Ausgangsspannung von bei einem maximalen Strom von regeln. Da der Lüfter laut Aufdruck bei einer Betriebsspannung von eine Stromaufnahme von aufweist, kann dieser mit dem Spannungsregler problemlos betrieben werden. Es stellt sich allerdings heraus, dass mit dem Aufbau die Spannung am LED-Panel zusammenbricht und dieses nicht mehr leuchtet. Also muss ein separates Netzteil verwendet werden. Damit ein gemeinsames Massepotential gegeben ist, werden alle Komponenten der Regelung (Lüfter, Sensor, Mikrocontroller) von dem Netzteil gespeist. Verwendet wird ein LED-Netzteil, das eine Ausgangsspannung von liefert. Die entworfene Schaltung zur Ansteuerung des Lüfters mittels PWM zeigt Abbildung 8.
-
Abbildung 8: Schaltung zur Ansteuerung des Lüfters.
Der Lüfter wird über einen Metall-Oxid-Halbleiter-Feldeffekttransistor (engl. metal-oxide-se- miconductor field-effect-transistor, kurz: MOSFET) gesteuert. Das "Gate" des MOSFETs wird zur Einschaltstrombegrenzung über einen Widerstand geladen. Der Widerstand dient der Erzeugung eines definierten Potentials am "Gate". Da es sich beim Lüfter um eine induktive Last handelt, ist außerdem eine sog. Freilaufdiode verbaut. In den Phasen, wo das PWM-Signal von "HIGH" auf "LOW" wechselt, entsteht in den Spulen des Lüfters eine hohe Induduktionsspannung. Zum Abbau dieser Spannung muss die Diode in Durchlassrichtung liegen. Der Test dieser Schaltung erfolgt auf einem Steckbrett und wird zunächst ohne gesonderte Konfiguration der Register des µC gestartet. Hier fällt auf, dass der Lüfter niederfrequent piept. Dies ist auf die geringe Frequenz des PWM-Signals zurückzuführen, welche laut Oszilloskopmessung bei ca. liegt. Zur Lösung des Problems bietet der µC des Arduino Nano die Möglichkeit, die Frequenz durch Setzen der Konfigurationsregister des Zähler/Zeitgeber-Bausteins zu erhöhen. Die Berechnungsvorschrift ist im Datenblatt wie folgt angegeben:
So kann bei einer gegebenen PWM-Auflösung von , einem Vorteiler von und einer Taktfrequenz von eine PWM-Frequenz von
erreicht werden. Eine erneute Oszilloskopmessung bestätigt diesen Wert und das Lüfterpiepen tritt nicht mehr auf.
Umsetzung und Integration der Hardware
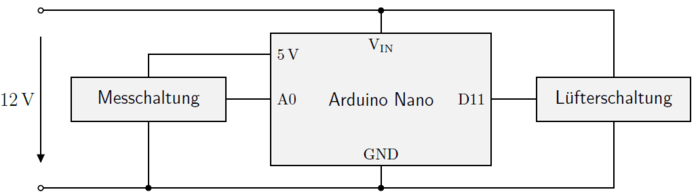
Für die Integration der Gesamtschaltung im Scheinwerfer eignet sich ein Steckbrett nicht, weshalb die Umsetzung auf einer Lochrasterplatine erfolgt. Der Arduino Nano wird nach Abbildung 9 in die Messschaltung und Lüfterschaltung integriert.
-
Abbildung 9: Integration des Arduino Nano in die Gesamtschaltung.
Ein auf dem Arduino integrierter Spannungsregler erlaubt die Spannungsversorgung über das LED-Netzteil an den Pins und . Die Messschaltung wird vom Pin betrieben und das Sensorsignal am analogen Eingang abgegriffen. Das PWM-Signal zum Schalten des MOSFETs der Lüfterschaltung wird am digitalen Ausgang erzeugt. Die fertige Platine zeigt Abbildung 10.
-
Abbildung 10: Verlötete Lochrasterplatine in Vorder- und Rückansicht.
Die grüne Schraubklemme links in der Vorderansicht dient der Spannungsversorgung mit dem LED-Netzteil. Die Messschaltung findet sich im roten Rechteck wieder und die Lüfterschaltung ist hellblau eingerahmt. Die Verknüpfungen der Bauelemente sind größtenteils mit Lötzinn vorgenommen worden. Lediglich bei größeren Distanzen werden Drähte verwendet.
Die Platine des LED-Netzteils wird aus Platzgründen zunächst aus dem Gehäuse entnommen und in ein eigens entworfenes, 3D-gedrucktes Gehäuse geklebt. Dazu werden die Kantenlängen der Platine mit einem Messschieber gemessen und auf Basis dieser Maße in SolidWorks ein 3D-Modell des neuen Gehäuses erstellt. Aus dem Modell lässt sich eine *.stl-Datei erstellen, aus der von einer weiteren Software g-Code generiert wird. Dieser erhält für einen 3D-Drucker interpretierbare Anweisungen zur additiven Fertigung des Gehäuses. Das Modell sowie das Ergebnis zeigt Abbildung 11.
-
Abbildung 11: Gehäuse für das Netzteil als 3D-Modell (links) und als 3D-gedrucktes Bauteil (rechts).
Zur Fixierung der Platine im Gehäuse wird Silikon verwendet. Die Integration des LED-Netzteils und der Lochrasterplatine im Scheinwerfer zeigt Abbildung 12. Das Netzteil des Scheinwerfers ist auf einer Kunststoffplatte verschraubt, welche auf der Oberseite Platz zum Einbau der Lochrasterplatine in Längsrichtung bietet. So wird der Luftstrom möglichst wenig beeinflusst. Außerdem ist auf der Unterseite Platz zum Verbau des LED-Netzteils, welches mit Wechselspannung versorgt wird (hellblaues und hellbraunes Kabel links mittig im Bild). Zur Fixierung wird zunächst doppelseitiges Klebeband verwendet. Die Komponenten werden danach ebenfalls mit Silikon an die Kunststoffplatte geklebt. Die zwei weißen Kabel in der Mitte des Bildes werden zur Spannungsversorgung mit der oben erwähnten grünen Klemme verschraubt.
-
Abbildung 12: Integration der Hardware im Scheinwerfer.
Falls es zu einem Ausfall des Arduinos kommt und entsprechend keine Kühlleistung vom Lüfter ausgeht, sorgt die bereits verbaute Platine mit dem zugehörigen NTC für ein Abschalten des LED-Panels. Durch Tests mit einem handelsüblichen Fön kann nachgewiesen werden, dass dies bei einer Paneltemperatur von passiert. Außerdem wird mit dem neuen Aufbau gewährleistet, dass die Verknüpfung und Helligkeitseinstellung mehrerer Godox SL60W Scheinwerfer mit der zugehörigen Fernbedienung funktionsfähig bleibt.
Modellbildung und Regelung des Systems
Dieser Teil beinhaltet die Erstellung eines Systemmodells, anhand dessen ein Regler ausgelegt werden kann. Dieser wird anschließend am Scheinwerfer in Betrieb genommen und optimiert.
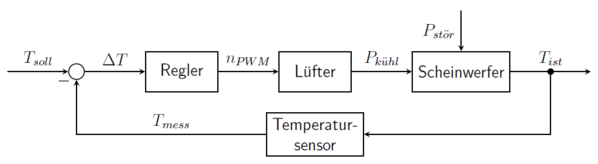
Regelziel und Regelkreis
Bei der Vorgehensweise zum Entwurf eines Reglers wird zunächst das Regelziel formuliert. Wie aus der Aufgabenstellung hervorgeht, ist die Regelgröße des Projekts die Temperatur des Scheinwerfers am LED-Panel (). Dadurch wird der Lüfter nicht in Abhängigkeit der eingestellten Helligkeitsstufe gesteuert, sondern temperaturabhängig geregelt. Ziel ist es, den vom Lüfter ausgehenden Lärm zu minimieren. Um lärmentwickelnde Drehzahlschwankungen zu vermeiden, sollte die Regelgröße möglichst präzise auf der Führungsgröße gehalten werden. Mit Störungen, auf die schnell reagiert werden muss, ist bei diesem trägen System nicht zu rechnen, weshalb ein gutes Führungsverhalten das primäre Ziel der Regelung ist. Ausgehend von der Regelgröße wird der Regelkreis sukzessive aufgebaut. Die Messgröße entspricht der mit dem NTC gemessenen Temperatur , sodass die Führungsgröße die Solltemperatur ist. Der Lüfter wird über ein PWM-Signal angesteuert, dessen Tastverhältnis durch Änderung des Wertes im Vergleichsregister der Zähler/Zeitgeber-Einheit des µCs variiert wird. Dieser Wert wird der Stellgröße zugeordnet, um den in der Simulation getesteten Regler genauso auf dem µC in Betrieb nehmen zu können. Die Stellgröße des Stellgliedes ist eine Kühlleistung , welche auf die Regelstrecke, also das dynamische System "Scheinwerfer", wirkt. Der Regelkreis sieht wie in Abbildung 13 dargestellt aus.
-
Abbildung 13: Temperaturregelkreis des Scheinwerfers.
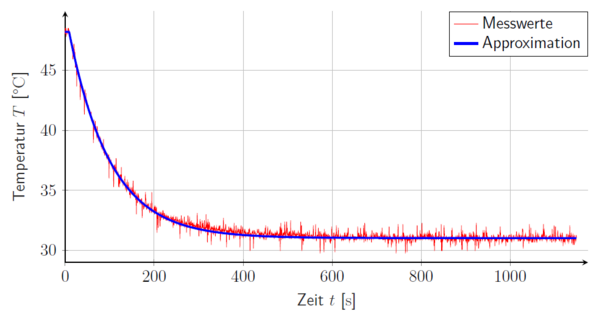
Aufnahme der Regelstrecke
Um den Regler in der Simulation auszulegen, ist es notwendig, das Verhalten der Regelstrecke zu kennen. Dies wird mit der experimentellen Modellbildung ermittelt. Dazu wird ein Einheitssprung auf die Eingangsgröße der Regelstrecke gegeben und die Ausgangsgröße aufgenommen. In diesem Anwendungsfall wird der Lüfter also mit maximalem Vergleichsregisterwert von bzw. einem Tastverhältnis von angesteuert. Der Scheinwerfer wird zuvor auf eine Temperatur von ca. (eingeschwungener Zustand) aufgeheizt. Die Sprungantwort zeigt Abbildung 14 in rot. Der blaue Verlauf stellt die bei der Sprungantwortmethode notwendige Approximation mit einem -Glied dar. Die Parameter der Übertragungsfunktion werden aus der Sprungantwort abgelesen.
-
Abbildung 14: Sprungantwort der Regelstrecke.
Es ergibt sich für die Verstärkung , für die Zeitkonstante und für die Totzeit , sodass die Regelstrecke folgendermaßen dargestellt werden kann:
Diese Übertragungsfunktion stellt die Basis für das weitere Vorgehen bei der Reglerauslegung dar. Die Einheiten werden bewusst weggelassen, damit die Laplace-Variable nicht mit der Einheit Sekunde verwechselt wird.
Reglerauslegung in der Simulation
Für dieses Projekt wird ein PI-Regler genutzt. Auf einen D-Anteil wird verzichtet, da das System mit der hohen Zeitkonstante sehr träge ist. Es sind keine schnellen Temperaturänderungen zu erwarten, auf die reagiert werden muss. Die Ermittlung der Reglerparameter erfolgt mittels der Einstellregeln nach Ziegler-Nichols und Chien, Hrones und Reswick. Für letztere Methode wird eine starke Dämpfung gewählt, d.h. die Temperatur soll nicht überschwingen. Außerdem soll das Führungsverhalten möglichst gut sein.
| Parameter | Ziegler-Nichols | Chien, Hrones, Reswick |
|---|---|---|
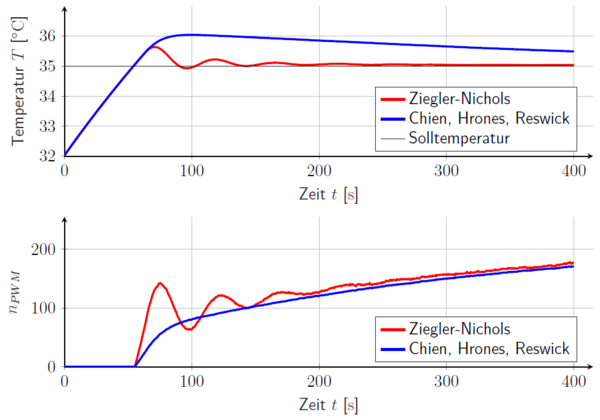
Mit diesen Werten kann in Simulink ein Vergleich der beiden Ergebnisse erfolgen (siehe Abbildung 15). Anders als bei der Aufnahme der Regelstrecke wird jetzt der Aufwärmvorgang des Scheinwerfers mit einem -Glied modelliert, da dies der Realität entspricht. Auf Basis verschiedener Messungen wird eine Solltemperatur von gewählt. Diese kann bei maximaler Helligkeitsstufe und einer Umgebungstemperatur von weniger als problemlos erreicht werden. Lediglich bei sommerlichen Temperaturen bleibt eine Regeldifferenz und der Lüfter läuft mit maximaler Drehzahl. Die im vorherigen Kapitel erwähnte ROI wird daher auf einen Bereich von bis festgelegt.
-
Abbildung 15: Vergleich der Regler in der Simulation.
Auffällig ist, dass der Regler mit den Parametern von Ziegler-Nichols ein Einschwingverhalten aufweist und von Chien, Hrones und Reswick sehr lange braucht, um den Sollwert zu erreichen. Das Stellgrößenverhalten ist bei dem Regler nach Chien, Hrones und Reswick weniger schwingend und verursacht damit auch weniger Lärm. Deshalb werden diese Parameter durch Ausprobieren weiter verbessert, sodass die Sollgröße schneller erreicht wird. Dazu wird die Zeitkonstante des I-Anteils sukzessive verringert. Es ergeben sich im Modell bis zu einem Wert von immer bessere Ergebnisse, d.h. die Solltemperatur wird bei nicht schwankender Stellgröße schneller erreicht (siehe Abbildung 16). Wird weiter verringert, ergibt sich ein unerwünschtes Einschwingverhalten.
-
Abbildung 16: Optimiertes Reglerverhalten in der Simulation.
Ausgehend von diesen Parametern wird der Regler am System in Betrieb genommen und weiter verbessert.
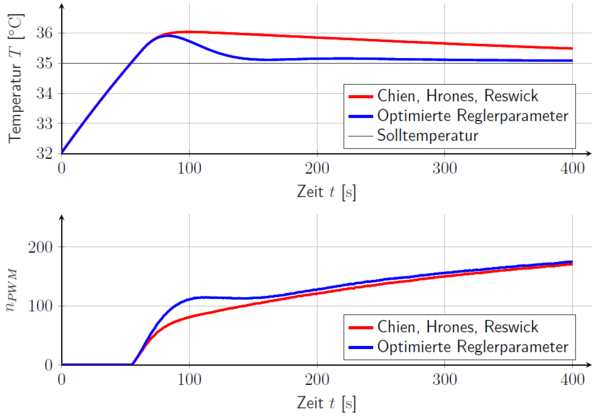
Inbetriebnahme der Regelung am Scheinwerfer
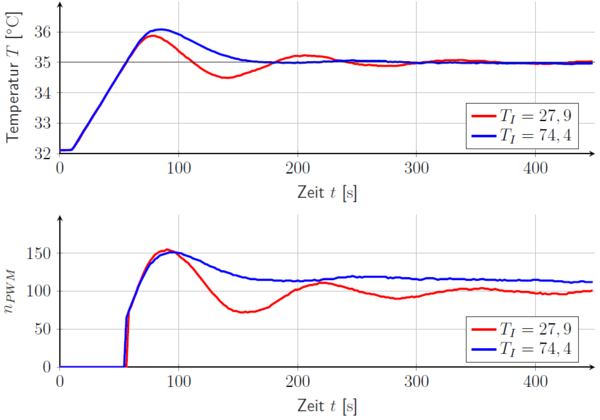
Mit den im Modell optimierten Reglerparametern ergibt sich ein Einschwingvorgang im Temperatur- und Stellgrößenverlauf. Daher wird die Zeitkonstante solange erhöht, bis der Regler die Sollgröße ohne signifikantes Einschwingen erreicht. Dabei ist es wichtig, den Scheinwerfer nach jedem neuen Test abkühlen zu lassen, um gleiche Rahmenbedingungen zu schaffen. Erst dann kann ein aussagekräftiger Vergleich der Ergebnisse durchgeführt werden. Bei einem Wert von tritt erstmalig ein gutes, nahezu schwingungsfreies Verhalten der Regelgröße auf. Ein Vergleich der Verläufe mit den im Modell und am System optimierten Parametern zeigt Abbildung 17.
-
Abbildung 17: Reglervergleich am realen System.
Es wird deutlich, dass die Solltemperatur vom blauen Verlauf schneller und mit nur einem anfänglichen Überschwinger erreicht wird. Außerdem ist der Stellgrößenverlauf hier deutlich stabiler und damit weniger lärmerzeugend. Durch Vergleich dieser Abbildung mit Abbildung 16 wird darüber hinaus erkenntlich, dass Realität und Modell nicht exakt übereinstimmen. Nichtsdestotrotz stellen die Modellergebnisse einen guten ersten Anhaltspunkt zur weiteren Optimierung dar. Die finalen Parameter des Reglers werden mit den Resultaten dieses Kapitels zu und gewählt.
Zusammenfassung und Ausblick
Es lässt sich festhalten, dass das Ziel der Arbeit erfüllt werden konnte. Der Lüfter läuft in Abhängigkeit von der gemessenen Temperatur nach einem kurzen Überschwinger mit nahezu konstanter Stellgröße, sodass der entstehende Lärm minimal gehalten wird. Damit können in Zukunft Videoaufnahmen ohne größere Störung vertont werden. Um das Ziel zu erreichen, konnte die im Studium erlernte Theorie praktisch angewendet werden. Dabei war besonders das Wissen in den Themengebieten Elektrotechnik, Messtechnik und Regelungstechnik von Nutzen, welches im Rahmen des Projekts außerdem erweitert werden konnte.
Verbesserungspotenzial besteht bei der Fertigung der Platine. Diese könnte z.B. mit dem Fräsbohrplotter der HSHL gefertigt werden, um die Schaltung platzsparender zu realisieren. Des Weiteren ist es evtl. möglich, den Regler mit einem präziseren Systemmodell weiter zu optimieren. Das Resultat könnte ein Regelgrößenverlauf mit kleinerem oder ganz ohne Überschwinger sein.
Literaturverzeichnis
- ↑ :distrelec.de, abgerufen am 15.11.2022
![Abbildung 1: Arduino Nano. [1]](/wiki/images/thumb/c/cd/NANO.jpg.png/356px-NANO.jpg.png)