Modellsimulation in Webots und Simulationen mit ROS2

Autoren: Arfat Kamal
Betreuer: Prof. Schneider
Art: Praxissemester
Projektlaufzeit: 02.11.2021-20.02.2022

Abb. 1 AlphaBot Simulation in Webots

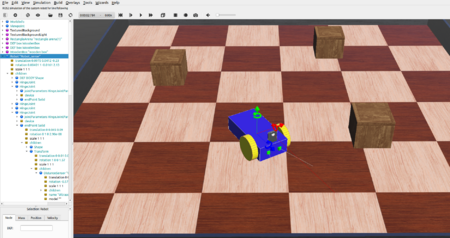
Introduction

In order to simulate, a 3D model of a 4 wheeled robot is created inside Webots first. That robot is simulated with a controller which is written in C inside the text editor of Webots. That robot is later imported in Webots in Ubuntu and customised with a
servo, an ultrasonic sensor and a caster wheel to resemble the Alphabot robot of our project. Finally, it is programmed with ROS2 and it runs in Webots as an obstacle avoiding robot.

Overview

Documentation

Creation of a 3D Model of a 4-Wheeled-Robot

Abb. 2 - 3D view of 4-Wheeled-Robot

A 4-Wheeled-Robot is created in Webots from scratch by following tutorial 6 in Cyberbotics. The robot consists of a body, 4 wheels and two distance sensors(IR sensors). The figure above shows the 3D view of the end result.

Co-ordinate System

Abb. 3 - Co-ordinates

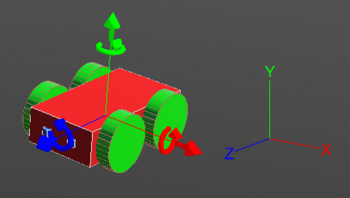
The co-ordinate system of the robot works exactly as the picture above depicts. The red arrow shows the X-axis and it defines the right and left of the robot. The green arrow shows the Y-axis and it can be used to move the robot upwards and downwards. The blue arrow is the Z-axis and it is related to forward and backward movement of the robot. By default the co-ordinates system is turned off in Webots. It can be turned on by following these steps:

 View >> Optional Rendering >> Show Coordinate System 

Or by simply pressing Ctrl+F1.

Top View in a Grid

Abb. 4 - Top View

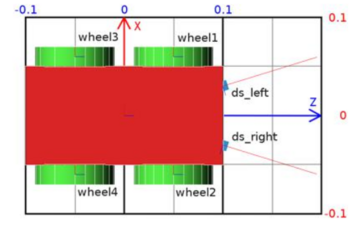
The figure above shows the top view of the robot. It is inside a grid to understand the dimensions of the robot. The dimension of the grid is 0.2 × 0.3 meters.

High Level Representation

Abb. 5 - High Level Representation

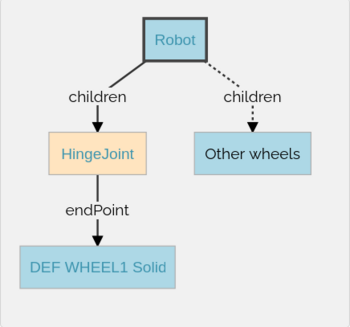
The picture above depicts the high level representation of the 4 wheeled robot. Here, Robot is the base node. The Robot node has four HingeJoint nodes. The HingeJoints are used as anchors to connect the wheels to the body of the robot. Each HingeJoint has a Solid node as endPoint. The Solid nodes are then modified into the wheels of the robot.

Low Level Representation

Abb. 6 - Low Level Representation

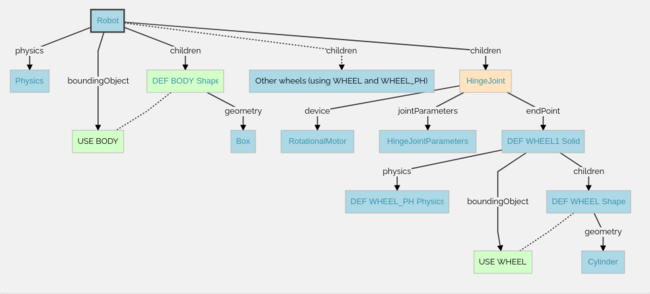
The figure above demonstrates the structure of the robot in details, how the 3D model is modeled in Weobts using the scene tree.

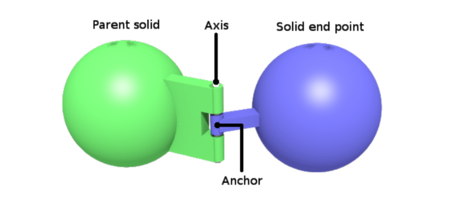
Representation of a HingeJoint

Abb. 7 - HingeJoint

Weiterführende Links

---

→ zurück zum Hauptartikel: Praxissemester Projektteam WS2021