Seminaraufgabe SoSe 2021: Einspurmodell Gruppe J: Unterschied zwischen den Versionen
| Zeile 218: | Zeile 218: | ||
== Ergebnis == | == Ergebnis == | ||
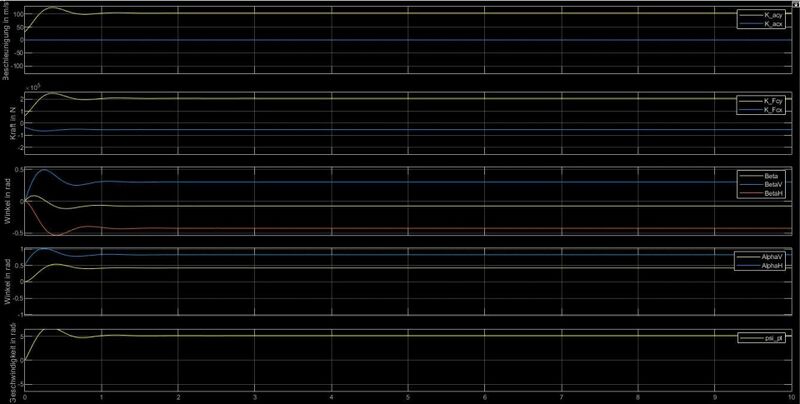
=== | === Manöverauswahl: Konstanter Lenkwinkel === | ||
[[Datei:Reifen | [[Datei:Reifen.png|left|mini|800px|Abb. 6: Reifen Gruppe J]] <br clear=all> | ||
== Zusammenfassung == | == Zusammenfassung == | ||
== Literaturverzeichnis == | == Literaturverzeichnis == | ||
Version vom 12. Juli 2021, 22:10 Uhr
Autoren: Orience Charnelle Mefenya, Sarra Khedhiri
Einleitung
Diese Seminaraufgabe wurde im Studiengang "Business and Systems Engineering" in der Lehrveranstaltung "System Design Engineering" von Prof. Göbel erledigt. Die Studierenden lernen in dieser Veranstaltung und während der Seminaraufgabe wie man das V-Modell entwickelt und anwendet. Das Ziel dieser Seminaraufgabe besteht darin ein lineares Einspurmodell zu entwickelt. Dieses Wiki-Artikel stellt die Arbeit der Gruppe J dar. Das Programm MATLAB - SIMULINK 2020a wurde für die Bearbeitung dieser Seminaraufgabe verwendet.
Vorgehensweise nach dem V-Modell
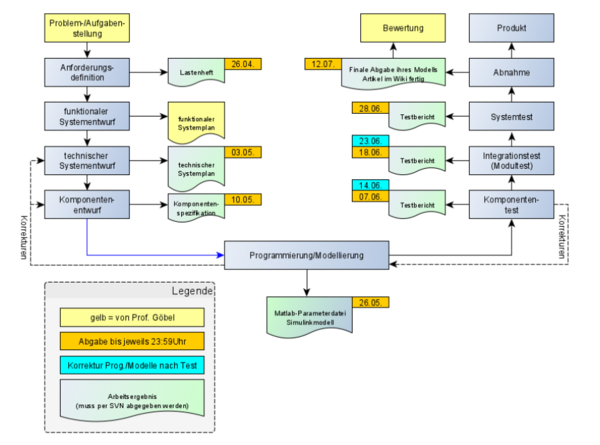
Anforderungsdefinition
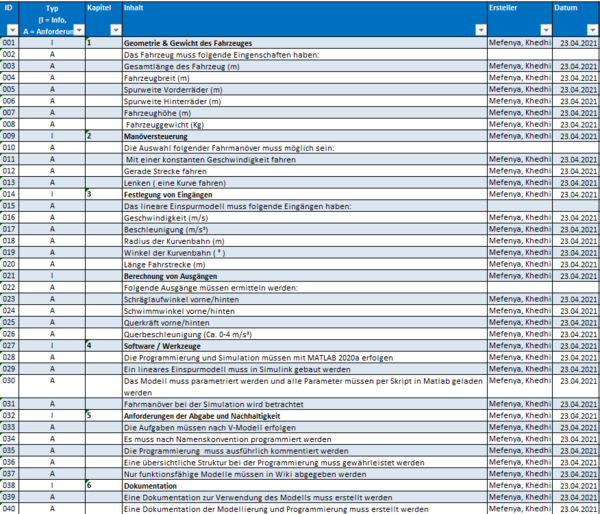
Für die Anforderungsdefinition wurde ein Lastenheft erstellt. Das Lastenheft beinhaltet alle notwendigen Informationen und Anforderungen für die Entwicklung des linearen Einspurmodell. Es wurden zum Beispiel die Geometrie, das Gewicht, die Eingänge, die Manöversteuerung, die Anforderungen der Abgaben, die Software und die Dokumentation festgelegt. Die von uns fesgelegten Anforderungen sind unter dem folgendem Link aufrufbar: Anforderungsdefinition Gruppe J
Funktionaler Systementwurf/Technischer Systementwurf
Damit wir ein technischer Systementwurf ableiten, hat uns Prof. Dr. Göbel ein funktionaler Systementwurf zur verfügung gestellt. Der abgeleitete technische Systementwurf besteht aus 3 Modulen, die nachfolgend beschrieben werden:
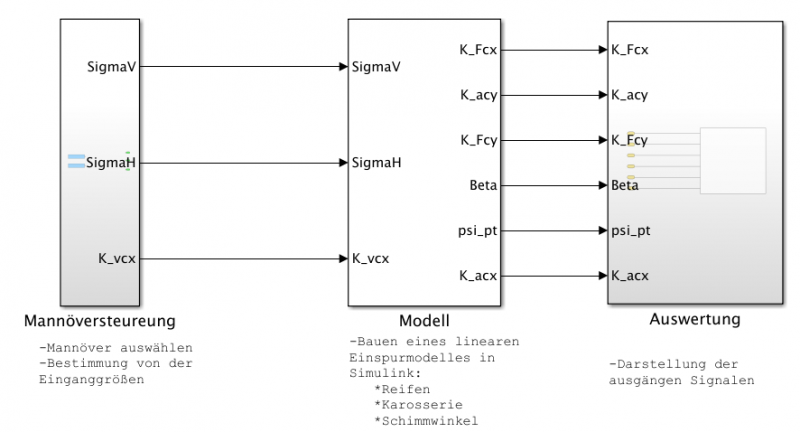
Der technische Systementwurf besteht aus folgenden drei Modulen:
- Manöversteuerung
- Manöver auswählen und Bestimmung von der Einganggrößen.
- Einspurmodel
- Das Bauen eines linearen Einspurmodell in Simulink und festlegung der Parameter für die Reifen, Karosserie,Schwimmwinkel.
- Auswertung
- Darstellung der Signale an den Ausgängen.
Der abgeleitete technische Systementwurf ist hier aufrufbar: Technischer Systementwurf Gruppe J
| Parameter | Beschreibung | Einheit |
|---|---|---|
| Lenkwinkel Vorderachse | ||
| Lenkwinkel Hinterachse | ||
| Schräglaufwinkel Vorderachse | ||
| Schräglaufwinkel Hinterachse | ||
| Fahrzeuglängsgeschwindigkeit im Fahrzeugschwerpunkt C | ||
| Fahrzeugquerbeschleunigung im Fahrzeugschwerpunkt C | ||
| Fahrzeufglängsbeschleunigung im Fahrzeugschwerpunkt C | ||
| Fahrzeugquerkraft im Fahrzeugschwerpunkt C | ||
| Fahrzeuglängskraft im Fahrzeugschwerpunkt C | ||
| Gierwinkelrate (Gierwinkelgeschwindigkeit) |
| Parameter | Beschreibung | Einheit | |
|---|---|---|---|
| Schwimmwinkel | |||
| Schwimmwinkelanteil Vorderachse | |||
| Schwimmwinkelanteil Hinterachse |
Komponentenspezifikation
Die Komponentenspezifikation definiert die Aufgabe, das Verhalten, den inneren Aufbau und die Schnittstellen der Komponenten. In den Submodulen Mannöversteuerung und Auswertung werden keine mathematischen Formeln verwendet. Das Submodul Modell wird, wie im technischen Systemplan beschrieben, in vier Komponenten unterteilt. Deren Funktionsweise soll im Folgenden mithilfe mathematischer Zusammenhänge erläutert werden. Bei der Herleitung wurden die in [2] beschriebenen Formeln verwendet, somit entstammen alle folgenden Herleitungen dieser Literatur.
Schwimmwinkel
Die Formel der Winkelgeschwindigkeit des Schwimmwinkels wird aus dem vereinfachten Schwerpunktsatz abgeleitet.
Durch Integration von ergibt sich der Schwimmwinkel des Fahrzeugs .
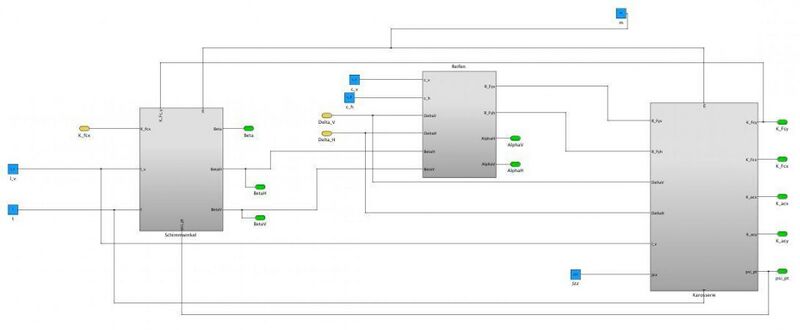
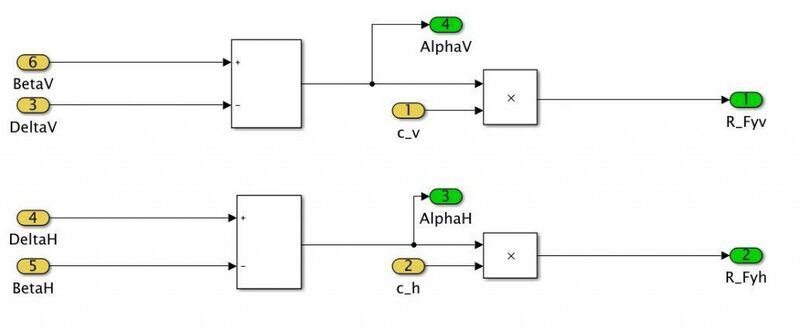
Reifen
Der Achs-Schräglaufwinkel ist der Winkel zwischen der Reifenlängsachse und dem Geschwindigkeitsvektor des Radmittelpunkts.
Basierend auf den Achs-Schräglaufwinkeln lassen sich zusammen mit der jeweiligen Achsseitensteifigkeit und , die Querkräfte an den Rädern bzw. Achsen berechnen.
Karosserie
Nach dem Skript wird beim linearen Einspurmodell von kleinen Winkeln ausgegangen und damit ergeben sich damit folgende Formeln für die Kräfte in x- und y-Richtung.
Aus den Kräften in x- und y-Richtung werden jeweils die Kräftesummen und gebildet. Durch Einsetzen des vorherigen Zusammenhanges können die folgenden Formeln gebildet werden.
Durch das Dividieren der jeweiligen Kräfte mit der Masse des Fahrzeugs ergeben sich die Fahrzeugbeschleunigungen in Quer- und Längsrichtung des Fahrzeugs (y- und x-Richtung).
Der Schwerpunktabstand der Hinterachse ergibt sich aus der Differenz von dem Radstand und dem Schwerpunktabstand zur Vorderachse .
Mithilfe des Drallsatzes lässt sich die Gierwinkelbeschleunigung berechnen.
Gierwinkel
Durch Integration der Gierwinkelbeschleunigung ergibt sich die Gierwinkelgeschwindigkeit .
Umsetzung
Für die Umsetzung werden erstmal die Parameter mithilfe eines MATLAB Skriptes festgelegt und dann werden diese Parameter für die Simulation in Simulink verwendet.
Parameterskript
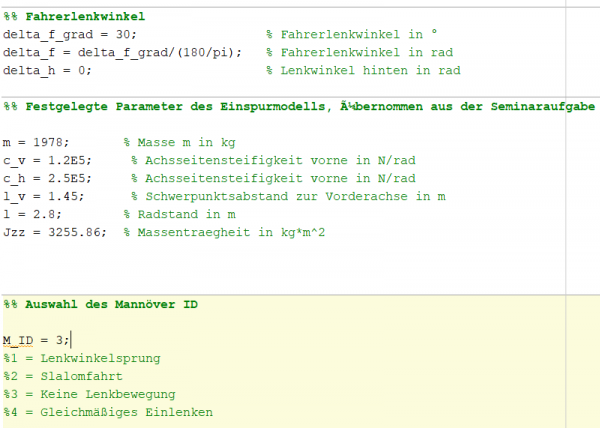
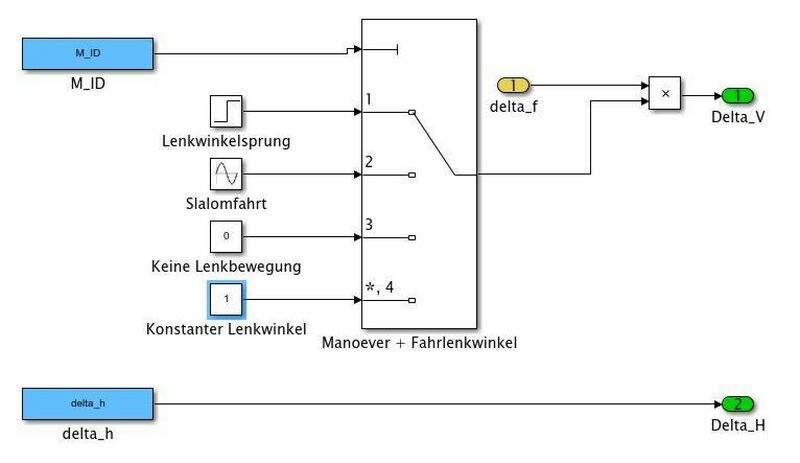
Die folgenden Manöver können für die Steuerungen ausgewählt werden. Diese Manöverauswahl ist in der obigen Parameterdatei (Abb. 3) in Matlab zu sehen, wobei man folgende Manöver auswählen kann:
- Lenkwinkelsprung
- Slalomfahrt
- Keine Lenkbewegung
- Gleichmäßiges Einlenken
Simulink Modell
Simulinkmodell Reifen
Simulinkmodell Manoever
Ergebnis
Manöverauswahl: Konstanter Lenkwinkel