BSF - Bahn- und Spurführung

Im Rahmen des SDE-Praktikums beinhaltet ein Arbeitsbereich die Bahnplanung und die Spurführung. Die Tätigkeit unterteilt sich in die Bereiche Bahnplanung und Autonome Längs- und Querregelung. Die Regelung ist im separaten Artikel beschrieben. In diesem soll das Querführungskonzept und die Bahnplanung dargestellt werden. Im Sommersemester 2014 wurde der Themenbereich von Daniel Block und Torben Petersen bearbeitet. Die Dokumentation beruht auf der Vorarbeit von Tobias Teicher, siehe Anleitung und Dokumentation Carolo-Cup 2013 Studiengang "Mechatronik" Schwerpunkt "System Design Engineering".

Querführungskonzept

Die Querführung des Fahrzeuges wird in zwei Bereiche unterteilt. Der erste Aspekt beinhaltet die Bahnplanung, die im folgenden in ihrer theoretischen Grundlage und der Umsetzung in Simulink dargestellt wird. Die Querregelung ist im entsprechenden Artikel Autonome Längs- und Querregelung beschrieben.
Als Grundlage für das Querführungskonzept dient die Sollbahn, die durch das Team OSE - Objekt- und Spurerkennung aufgrund der Analyse der zu fahrenden Strecke mit Hilfe eines Polynoms zweiten Gerades, das durch die Parameter a, b und c eindeutig beschrieben ist, zur Verfügung gestellt wird. Da in dieser Anwendung aufgrund der Geometrie des Fahrzeugs ein Vergleich der Soll- und Ist-Bahn nicht sinnvoll ist, muss ein Punkt auf der Bahn in der Vorrausschauweite x prädiziert werden, an dem sich das Fahrzeug bei idealem Lenkwinkel und der aktuellen Geschwindigkeit befinden würde. Der ideale Lenkwinkel kann aber nicht bestimmt werden. Aus diesem Grund muss eine Abschätzung der Querabweichung von der einfachen Geradeausfahrt getroffen werden. Dabei wird der derzeitige Lenkwinkel als Referenz verwendet. Die Regeldifferenz des Querreglers bildet sich somit aus dem Punkt auf der Sollbahn und der prädizierten Positionsabschätzung. Die Vorrausschauweite x wird abhängig von der aktuellen Geschwindigkeit des Fahrzeugs berechnet. Der dazu verwendete Umrechnungsfaktor kann in der Parameterdatei param_BSF.m über den Parameter PAR_BSFQuer_GainVorausschauweite_f64 eingestellt werden, der aktuelle Wert ist 0.2.

Sollbahnbestimmung

Im Folgenden soll die Bestimmung des Punktes auf der Sollbahn beschrieben werden. Die Bahn wird als ein Polynom zweiten Gerades, einer Parabel, approximiert. Die allgemeine Formel lautet:
$y = a \cdot x^2 + bx + c \qquad(1)$
Die Abbildung Schema der Sollbahn zeigt die Sollkurve im Fahrzeug-Koordinatensystem. Auch die Lage des Sollpunktes auf der Kurve ist dort qualitativ zu sehen.

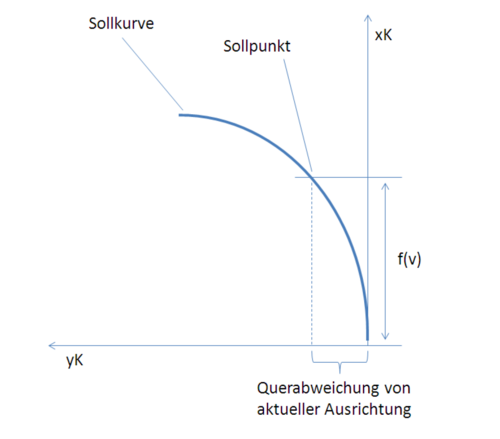
Die Bestimmung des prädizierten Punktes des Fahrzeuges auf der Ist-Bahn geschieht unter folgender Annahme: Ist der Lenkwinkel des Fahrzeuges gleich Null, existiert zwischen prädiziertem Ist-Punkt und der aktuellen Ausrichtung des Fahrzeuges keine Querabweichung. Fährt das Fahrzeug nicht exakt geradeaus, befindet es sich auf einer Kreisbahn, die bei stationär statischem Lenkwinkel konstant ist.
Der Radius dieser Kreisbahn lässt sich aus der stationären Gierrate und der Geschwindigkeit wie folgt bestimmen:
$r=\frac{v_0}{\dot\psi} \qquad(2)$
Die Abbildung Schema der Istbahn zeigt die prädizierte Istbahn im Fahrzeug-Koordinatensystem und den Zusammenhang zwischen Querabweichung y und Vorrausschauweite x.

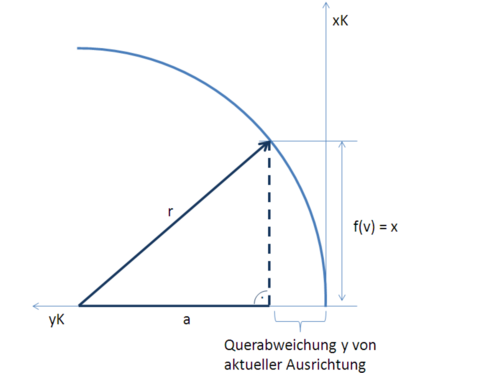
Zur Bestimmung der Querabweichung y wird der in der Skizze erkenntliche Zusammenhang zwischen dem Kreisradius r und der Vorausschauweite x verwendet. Mit dem Satz des Phythagoras kann a wie folgt bestimmt werden:
$r^2=x^2+a^2\Leftrightarrow a^2=r^2-x^2\Leftrightarrow a=\sqrt{r^2-x^2}\qquad(3)$

Die Querabweichung y kann aus r und a bestimmt werden:
$y=r-a \qquad(4)$

Da die Vorrausschauweite x unabhängig vom derzeitigen Kurvenradius r bestimmt wird, kann der Ausdruck unter der Wurzel in (3) negativ sein. Weil diese Berechnung unzulässig wäre, wird vorbeugend das Ergebnis der Vorrausschauweitenberechnung mit einer Sättigungsfunktion begrenzt, die maximal 80 % des aktuellen Kurvenradius annimmt. Dieser Wert (80 % = 0.8) kann über den Parameter PAR_BSFQuer_VorrausschauBegrenzung_f64 eingestellt werden.
Die Querabweichung der Sollbahn und die Querabweichung der Istbahn, jeweils bezogen auf die aktuelle Ausrichtung des Fahrzeuges, ergeben die Regeldifferenz für den Querregler. Aufgrund der Differenz zwischen Sollbahn und Istbahn bringt dieses Konzept eine bleibende Regelabweichung in der Kurve mit sich. Diese ist nur dann Null, wenn das Fahrzeug sich in der Geradeausfahrt befindet.

Status Quo

In dem oben beschriebenen Konzept wird zur Bestimmung der Istbahn die Gierrate benötigt. Gemäß der Vorarbeit früherer Teams ist das Signal des Gyro-Sensors derzeit nicht verwendbar. Alternativ wurde daher ein neuer Ansatz zur Bestimmung der Regeldifferenz gewählt. Dabei wird angenommen, dass ohne Stellgrößenberechnung des Reglers das Fahrzeug auf einer Geraden fährt. Dadurch ergibt sich die Vereinfachung dahingehend, dass die prädizierte Istbahn des Fahrzeugs und die aktuelle Ausrichtung identisch sind, also dazwischen keine Querabweichung vorliegt. Als Regeldifferenz ergibt sich somit die Querabweichung der Sollbahn von der aktuellen Ausrichtung des Fahrzeugs.

Die Querregelung wird im separaten Artikel Autonome Längs- und Querregelung beschrieben.

Einspurmodell

Für die effikitve Nutzung des Offline-Modells in der Simulation ist eine Anpassung des Einspurmodells (ESM) an das Fahrzeug notwendig, damit das Modell der Realität so nah wie möglich kommt. Dazu müssen die einzelnen Parameter des Modells entsprechend bestimmt werden. Die aktuellen Werte sind in den Parameterdateien param_ESM_offline.m und param_CAR.m hinterlegt und werden somit vom Modell verwendet.

Größen des Einspurmodells

Im Folgenden sollen die Parameter des Modells kurz vorgestellt werden.

• Radstand des Fahrzeugs, wird im ESM mit l bezeichnet
• Abstand des Schwerpunktes des Fahrzeuges von dem vordersten Punkt l_v
• Abstand des Schwerpunktes des Fahrzeuges von dem hintersten Punkt l_h
• Masse des Fahrzeugs m
• Massenträgheitsmoment um die Z-Achse des fahrzeugfesten Koordinatensystems J
• Steifigkeit der Vorderachse c_v
• Steifigkeit der Hinterachse c_h

Bestimmung der Parameter

Nun wird für die einzelnen Parameter die Bestimmung der jeweiligen Größen vorgestellt.
Radstand l
Der Radstand lässt sich durch eine Messung mit einem Messschieber bestimmen. Es ist dabei der Abstand vom vorderen zum hinteren Achsenmittelpunkt zu messen. Für das Einspurmodell ist die Gesamtlänge, also inklusive der vorderen und hinteren Überhänge, nicht von Bedeutung.
Abstand des Schwerpunktes des Fahrzeuges von den äußeren Punkten l_v und l_h
Zur Bestimmung der Abstände wird das Fahrzeug an den beiden Achsen mit zwei Waagen gewogen. Aus dem Verhältnis der bestimmten Maßen lässt sich die Lage des Schwerpunktes in Längsrichtung des Fahrzeugs bestimmen.
Masse des Fahrzeugs m
Die Gesamtmasse ergibt sich aus der Summe der zwei zuvor bestimmten Teilmassen.
Massenträgheitsmoment um die Z-Achse J_z
Das Massenträgheitsmoment um die Z-Achse J_z wird bestimmt unter der Annahme, dass das Fahrzeug geometrisch einem Quader ähnelt.
Für die Bestimmung der Steifigkeiten und die Feinjustierung des Modells wird das Fahrzeug, das die Regelstrecke darstellt, mit einer Sprungantwort für einen Sprung des Lenkwinkels analysiert. Dazu wird die Gierrate des Fahrzeugs während des Sprungsignals gemessen. Das ESM lässt sich anhand dieser Messdaten parametrisieren, indem das Übertragungsverhalten des Fahrzeugs den vom Modell errechneten Daten vergleichend gegenübergestellt wird.

Ausblick

• Messung der Gierrate mit neuem Gierraten-Sensor
• Auslegung des ESM durch Justierung der Größen J, c_v und c_h
• Konzept für Hindernisumfahrung

Autoren: Daniel Block und Torben Petersen im Sommersemester 2014

---

→ zurück zum Hauptartikel: Praktikum SDE