BSF - Bahn- und Spurführung: Unterschied zwischen den Versionen
Einleitung |
Sollbahnbestimmung |
||
| Zeile 3: | Zeile 3: | ||
==Querführungskonzept== | ==Querführungskonzept== | ||
Die Querführung des Fahrzeuges wird in zwei Bereiche unterteilt. Der erste Aspekt beinhaltet die Bahnplanung, die im folgenden in ihrer theoretischen Grundlage und der Umsetzung in Simulink dargestellt wird. Die Querregelung ist im entsprechenden Artikel [[Autonome Längs- und Querregelung|Autonome Längs- und Querregelung]] beschrieben. <br> | Die Querführung des Fahrzeuges wird in zwei Bereiche unterteilt. Der erste Aspekt beinhaltet die Bahnplanung, die im folgenden in ihrer theoretischen Grundlage und der Umsetzung in Simulink dargestellt wird. Die Querregelung ist im entsprechenden Artikel [[Autonome Längs- und Querregelung|Autonome Längs- und Querregelung]] beschrieben. <br> | ||
Als Grundlage für das Querführungskonzept dient die Sollbahn, die durch das Team ''OSE - Objekt- und Spurerkennung'' aufgrund der Analyse der zu fahrenden Strecke mit Hilfe eines Polynoms zweiten Gerades, das durch die Parameter ''a'', ''b'' und ''c'' eindeutig beschrieben ist, zur Verfügung gestellt wird. Da in dieser Anwendung aufgrund der Geometrie des Fahrzeugs ein Vergleich der Soll- und Ist-Bahn nicht sinnvoll ist, muss ein Punkt auf der Bahn in der Vorrausschauweite ''x'' prädiziert werden, an dem sich das Fahrzeug bei idealem Lenkwinkel und der aktuellen Geschwindigkeit befinden würde. Der ideale Lenkwinkel kann aber nicht bestimmt werden. Aus diesem Grund muss eine Abschätzung der Querabweichung von der einfachen Geradeausfahrt getroffen werden. Dabei wird der derzeitige Lenkwinkel als Referenz verwendet. Die Regeldifferenz des Querreglers bildet sich somit aus dem Punkt auf der Sollbahn und der prädizierten Positionsabschätzung. Die Vorrausschauweite ''x'' wird abhängig von der aktuellen Geschwindigkeit des Fahrzeugs berechnet. | Als Grundlage für das Querführungskonzept dient die Sollbahn, die durch das Team ''OSE - Objekt- und Spurerkennung'' aufgrund der Analyse der zu fahrenden Strecke mit Hilfe eines Polynoms zweiten Gerades, das durch die Parameter ''a'', ''b'' und ''c'' eindeutig beschrieben ist, zur Verfügung gestellt wird. Da in dieser Anwendung aufgrund der Geometrie des Fahrzeugs ein Vergleich der Soll- und Ist-Bahn nicht sinnvoll ist, muss ein Punkt auf der Bahn in der Vorrausschauweite ''x'' prädiziert werden, an dem sich das Fahrzeug bei idealem Lenkwinkel und der aktuellen Geschwindigkeit befinden würde. Der ideale Lenkwinkel kann aber nicht bestimmt werden. Aus diesem Grund muss eine Abschätzung der Querabweichung von der einfachen Geradeausfahrt getroffen werden. Dabei wird der derzeitige Lenkwinkel als Referenz verwendet. Die Regeldifferenz des Querreglers bildet sich somit aus dem Punkt auf der Sollbahn und der prädizierten Positionsabschätzung. Die Vorrausschauweite ''x'' wird abhängig von der aktuellen Geschwindigkeit des Fahrzeugs berechnet. Der dazu verwendete Umrechnungsfaktor kann in der Parameterdatei ''param_BSF.m'' über den Parameter ''PAR_BSFQuer_GainVorausschauweite_f64'' eingestellt werden, der aktuelle Wert ist 0.2. | ||
===Sollbahnbestimmung=== | |||
Im Folgenden soll die Bestimmung des Punktes auf der Sollbahn beschrieben werden. Die Bahn wird als ein Polynom zweiten Gerades, einer Parabel, approximiert. Die allgemeine Formel lautet: <br> | |||
<math>y = a \cdot x^2 + bx + c \qquad(1)</math><br> | |||
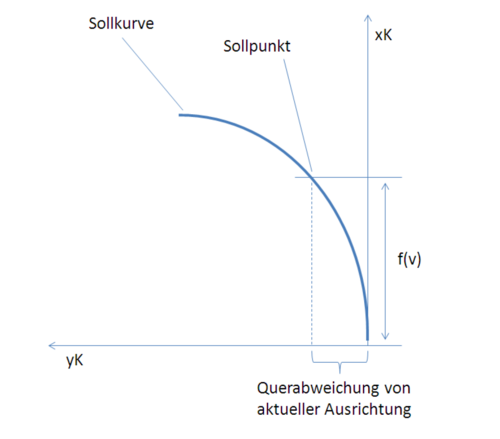
Die Abbildung ''Schema der Sollbahn'' zeigt die Sollkurve im Fahrzeug-Koordinatensystem. Auch die Lage des Sollpunktes auf der Kurve ist dort qualitativ zu sehen. | |||
[[Datei:Schema der Sollbahn.PNG|500 px|center]] | |||
Die Bestimmung des prädizierten Punktes des Fahrzeuges auf der Ist-Bahn geschieht unter folgender Annahme: Ist der Lenkwinkel des Fahrzeuges gleich Null, existiert zwischen prädiziertem Ist-Punkt und der aktuellen Ausrichtung des Fahrzeuges keine Querabweichung. Fährt das Fahrzeug nicht exakt geradeaus, befindet es sich auf einer Kreisbahn, die bei stationär statischem Lenkwinkel konstant ist.<br> | |||
Der Radius dieser Kreisbahn lässt sich auf der stationären Gierrate und Geschwindigkeit wie folgt bestimmen: <br> | |||
<math>r=\frac{v_0}{\dot\psi} \qquad(2)</math><br> | |||
Die Abbildung ''Schema der Istbahn'' zeigt die prädizierte Istbahn im Fahrzeug-Koordinatensystem und den Zusammenhang zwischen Querabweichung ''y'' und Vorrausschauweite ''x''. | |||
[[Datei:Schema der Istbahn.PNG|500 px|center]] | |||
Zur Bestimmung der Querabweichung ''y'' wird der in der Skizze erkenntliche Zusammenhang zwischen dem Kreisradius ''r'' und der Vorausschauweite ''x'' verwendet. Mit dem ''Satz des Phythagoras'' kann a wie folgt bestimmt werden: <br> | |||
<math>r^2=x^2+a^2\Leftrightarrow a^2=r^2-x^2\Leftrightarrow a=\sqrt{r^2-x^2}\qquad(3)</math><br><br> | |||
Die Querabweichung ''y'' kann aus ''r'' und ''a'' bestimmt werden:<br> | |||
<math>y=r-a \qquad(4)</math><br> | |||
Version vom 16. Mai 2014, 10:59 Uhr
Im Rahmen des SDE-Praktikums beinhaltet ein Arbeitsbereich die Bahnplanung und die Spurführung. Die Tätigkeit unterteilt sich in die Bereiche Bahnplanung und Autonome Längs- und Querregelung. Die Regelung ist im separaten Artikel beschrieben. In diesem soll das Querführungskonzept und die Bahnplanung dargestellt werden. Im Sommersemester 2014 wurde der Themenbereich von Daniel Block und Torben Petersen bearbeitet. Die Dokumentation beruht auf der Vorarbeit von Tobias Teicher, siehe Anleitung und Dokumentation Carolo-Cup 2013 Studiengang "Mechatronik" Schwerpunkt "System Design Engineering".
Querführungskonzept
Die Querführung des Fahrzeuges wird in zwei Bereiche unterteilt. Der erste Aspekt beinhaltet die Bahnplanung, die im folgenden in ihrer theoretischen Grundlage und der Umsetzung in Simulink dargestellt wird. Die Querregelung ist im entsprechenden Artikel Autonome Längs- und Querregelung beschrieben.
Als Grundlage für das Querführungskonzept dient die Sollbahn, die durch das Team OSE - Objekt- und Spurerkennung aufgrund der Analyse der zu fahrenden Strecke mit Hilfe eines Polynoms zweiten Gerades, das durch die Parameter a, b und c eindeutig beschrieben ist, zur Verfügung gestellt wird. Da in dieser Anwendung aufgrund der Geometrie des Fahrzeugs ein Vergleich der Soll- und Ist-Bahn nicht sinnvoll ist, muss ein Punkt auf der Bahn in der Vorrausschauweite x prädiziert werden, an dem sich das Fahrzeug bei idealem Lenkwinkel und der aktuellen Geschwindigkeit befinden würde. Der ideale Lenkwinkel kann aber nicht bestimmt werden. Aus diesem Grund muss eine Abschätzung der Querabweichung von der einfachen Geradeausfahrt getroffen werden. Dabei wird der derzeitige Lenkwinkel als Referenz verwendet. Die Regeldifferenz des Querreglers bildet sich somit aus dem Punkt auf der Sollbahn und der prädizierten Positionsabschätzung. Die Vorrausschauweite x wird abhängig von der aktuellen Geschwindigkeit des Fahrzeugs berechnet. Der dazu verwendete Umrechnungsfaktor kann in der Parameterdatei param_BSF.m über den Parameter PAR_BSFQuer_GainVorausschauweite_f64 eingestellt werden, der aktuelle Wert ist 0.2.
Sollbahnbestimmung
Im Folgenden soll die Bestimmung des Punktes auf der Sollbahn beschrieben werden. Die Bahn wird als ein Polynom zweiten Gerades, einer Parabel, approximiert. Die allgemeine Formel lautet:
Die Abbildung Schema der Sollbahn zeigt die Sollkurve im Fahrzeug-Koordinatensystem. Auch die Lage des Sollpunktes auf der Kurve ist dort qualitativ zu sehen.
Die Bestimmung des prädizierten Punktes des Fahrzeuges auf der Ist-Bahn geschieht unter folgender Annahme: Ist der Lenkwinkel des Fahrzeuges gleich Null, existiert zwischen prädiziertem Ist-Punkt und der aktuellen Ausrichtung des Fahrzeuges keine Querabweichung. Fährt das Fahrzeug nicht exakt geradeaus, befindet es sich auf einer Kreisbahn, die bei stationär statischem Lenkwinkel konstant ist.
Der Radius dieser Kreisbahn lässt sich auf der stationären Gierrate und Geschwindigkeit wie folgt bestimmen:
Die Abbildung Schema der Istbahn zeigt die prädizierte Istbahn im Fahrzeug-Koordinatensystem und den Zusammenhang zwischen Querabweichung y und Vorrausschauweite x.
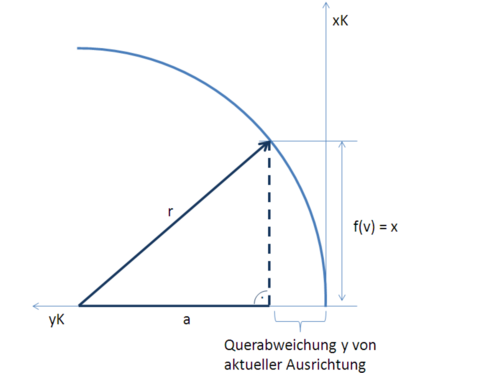
Zur Bestimmung der Querabweichung y wird der in der Skizze erkenntliche Zusammenhang zwischen dem Kreisradius r und der Vorausschauweite x verwendet. Mit dem Satz des Phythagoras kann a wie folgt bestimmt werden:
Die Querabweichung y kann aus r und a bestimmt werden: