Signalverarbeitende Systeme - L10: Koordinatentransformation: Unterschied zwischen den Versionen
| Zeile 169: | Zeile 169: | ||
|} | |} | ||
= Übung 10.5: KOS-Trafo: Homogene transformationsmatrix, Inverse Transformation = | = Übung 10.5: KOS-Trafo: Homogene transformationsmatrix, Inverse Transformation = | ||
Mit einem LiDAR Sensor wird die Fahrt eines Roboters vermessen. | Mit einem LiDAR Sensor wird die Fahrt eines Roboters vermessen. Als digitale Karte liegen die Punkte des äußeren und inneren Fahrbahnrandes vor. | ||
Gegeben sind: | '''Aufgaben:''' | ||
# Zeichnen | |||
'''Gegeben sind:''' | |||
* <math>{^{T}}\vec{r}_{0,W} = \left( \begin{array}{c} | * <math>{^{T}}\vec{r}_{0,W} = \left( \begin{array}{c} | ||
-4,7710\\ | -4,7710\\ | ||
| Zeile 192: | Zeile 195: | ||
0,03 | 0,03 | ||
\end{array}\right)</math> m: Objektposition im T-KOS in m | \end{array}\right)</math> m: Objektposition im T-KOS in m | ||
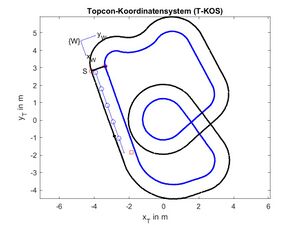
[[Datei:SigSys_UE10_5_T_KOS.jpg|ohne|mini|300px|Abb. 6: Fahrbahn im T-KOS]] | |||
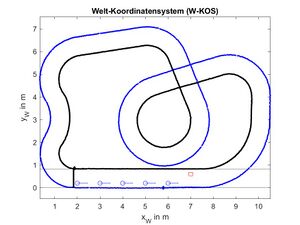
[[Datei:SigSys_UE10_5_W_KOS.jpg|ohne|mini|300px|Abb. 7: Fahrbahn im W-KOS]] | |||
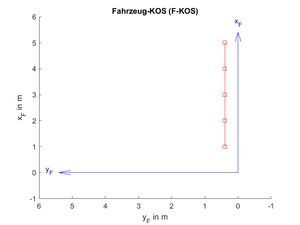
[[Datei:SigSys UE10 5 F KOS.jpg|ohne|mini|300px|Abb. 8: Objektposition im F-KOS]] | |||
'''Notwendige Dateien:''' | '''Notwendige Dateien:''' | ||
* [https://svn.hshl.de/svn/BSE_SigSys/trunk/Uebung/L10_Koordinatentransformation/AussenLinie.mat <code>AussenLinie.mat</code>] | * [https://svn.hshl.de/svn/BSE_SigSys/trunk/Uebung/L10_Koordinatentransformation/AussenLinie.mat <code>AussenLinie.mat</code>] | ||
Version vom 26. Mai 2025, 13:50 Uhr
| Dozent: | Prof. Dr.-Ing. Schneider |
| Lehrveranstaltung: | Signalverarbeitende Systeme |
| Modul | Signalverarbeitende Systeme und Systems Design Engineering |
| Modulbezeichnung: | BSE-M-2-1.06 |
| Modulverantwortung: | Prof. Ulrich Schneider |
| Vorlesung: | Invertierter Klassenraum, Montag, 10:00 - 11:30 Uhr |
| Übung: | Montag, 11:45 - 12:30 Uhr |
| Ort: | Labor L3.1-E00-120 |
Übung 10.1: KOS-Trafo: Rotation+Translation, Inverse Transformation
Das Lösungsvideo finden Sie auf der Lernplattform. Gegeben is der Ortsvektor zum Punkt P sowie der Rotationswinkel um die Z-Achse.
- Führen Sie über eine homogene Translation eine Rotation um den Winkel und eine Translation um den Vektor aus.
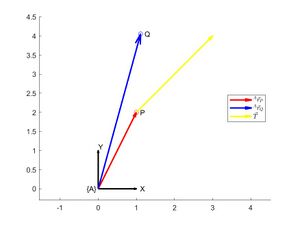
- Zeichnen Sie den transformierten Punkt Q und dessen Ortsvektor ein (vgl. Abb. 1).
- Berechnen Sie anschließend die inverse Translation
Gegeben sind:
Arbeitsergebnis: KOStrafo.m
| Musterlösung 10.1 |
%% Gegeben
A_r_P = [1;2;3;1]; % Ortsvektor zum Punkt P in KOS A
% Translation
T = [2;2;0]'; % Translationsvektor
S = 1; % Skalierungsfaktor
P = [0 0 0]; % Perspektiventrafo
Gamma = 50; % Rotationswinkel im deg
R = [cosd(Gamma) -sind(Gamma) 0;sind(Gamma) cosd(Gamma) 0; 0 0 1]; % Rotationsmatrix
D = zeros(4,4); % Homogene Transformation
D(1:3,1:3)= R;
D(1:3, 4) = T;
D(4,4) = S;
D(4,1:3) = P
A_r_Q = D * A_r_P % KOS-Trafo
%% Inverse Transformation
A_r_P2 = inv(D)*A_r_Q
%% Ergebnisdarstellung
figure
hold on
quiver(0,0,1,0,'LineWidth',2,'Color','black','AutoScale','off'); % x-Achse
text(1.1,0,'X')
quiver(0,0,0,1,'LineWidth',2,'Color','black','AutoScale','off'); % y-Achse
text(0,1.1,'Y')
h1 = quiver(0,0,A_r_P(1),A_r_P(2),'LineWidth',2,'Color','r','AutoScale','off'); % Ursprungsvektor
plot(A_r_P(1),A_r_P(2),'ro')
text(A_r_P(1)+0.1,A_r_P(2),'P')
h2 = quiver(0,0,A_r_Q(1),A_r_Q(2),'LineWidth',2,'Color','b','AutoScale','off'); % Vektor nach Trafo
text(A_r_Q(1)+0.1,A_r_Q(2),'Q')
plot(A_r_Q(1),A_r_Q(2),'bo')
h3 = quiver(A_r_P(1),A_r_P(2),T(1),T(2),'LineWidth',2,'Color','y','AutoScale','off'); % Translationsvektor
axis equal
legend([h1,h2,h3],{'$^A\vec{r}_P$','$^A\vec{r}_Q$','$\vec{T}$'},'Interpreter','latex','Location','east')
text(-0.3,0,'\{A\}')
ylim([-0.3 4.5])
|
Übung 10.2: 2-fache Koordinatentransformation
Gegeben sind:
- : Ortsvektor zum Punkt P im KOS A
- : Translationsvektor KOS B zum KOS A im B-KOS
- : Translationsvektor KOS C zum KOS B im C-KOS
- KOS A ist gegenüber KOS B um 10° um die Z-Achse gedreht.
- KOS B ist gegenüber KOS C um 10° um die Z-Achse gedreht.
Aufgaben:
- Bestimmen Sie die Vektoren und .
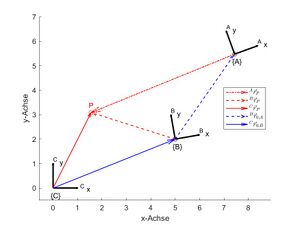
- Erstellen Sie ein Ergebnisbild gemäß Abb. 2.
Arbeitsergebnis: Transformationsarithmetik.m
| Musterlösung 10.2 |
| Das Lösungsvideo finden Sie auf der Lernplattform. |
Übung 10.3: Transformationsarithmetik
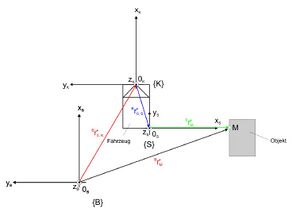
Ein autonomes Fahrzeug erkennt mit einem hinten rechts montierten Infrarot-Sensor ein Objekt am Messpunkt M. Die Messung erfolgt im Sensorkoordinatensystem {S}. Dieses Fahrzeug besitzt ein körperfeste Koordinatensystem {K} mit dem Ursprung am Mittelpunkt des vorderen Stoßfängers. Die Position und Lage (Pose) des Fahrzeugs im Bezugskoordinatensystem {B} ist bekannt. Abb. 3 zeigt eine mögliche Situation.
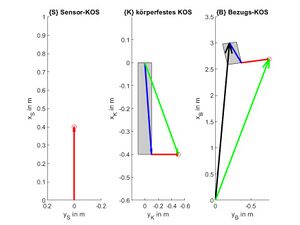
Bestimmen Sie den Ortsvektor zum Objekt im Bezugskoordinatensystem und zeichnen Sie mit MATLAB®die Szene (vgl. Abb. 4) in den drei Koordinatensystemen
- Sensorkoordinatensystem {S},
- körperfestes Koordinatensystem {K} und
- Bezugskoordinatensystem {B} .
Hinweis: In der Fahrzeugtechnik wird die Z-Achse antiparallel zum Gravitationsvektor angenommen: .
Gegeben sind:
- m: Messwert des IR-Sensors
- Der Winkel zwischen und beträgt 90°.
- m
- Der Winkel zwischen und beträgt 10°.
- Das Objekt hat eine Länge von 30 cm und eine Breite von 20 cm.
- Das Fahrzeug hat eine Länge von 40 cm und eine Breite von 20 cm.
- Die detektierte Objektkante ist parallel zu ().
- Der IR-Sensor erfasst die Längsseite des Objektes.
Arbeitsergebnis: TransformationsarithmetikMobileRobotik.m
| Musterlösung 10.3 |
| Das Lösungsvideo finden Sie auf der Lernplattform. |
Übung 10.4: Darstellung der LiDAR Messdaten
Schreiben Sie ein Skript ZeigeMessdaten, welches die gemessenen Streckendaten der Datei LiDAR.mat darstellt.
Gehen Sie in nachfolgenden Schritten vor:
- Laden Sie die Messdaten.
- Stellen Sie die Messwerte der Datei (x,y) als rote Punkte dar.
- Das KOS ist in Fahrtrichtung x-Positiv und die y-Achse zeigt nach links (vgl. Abb. 5).
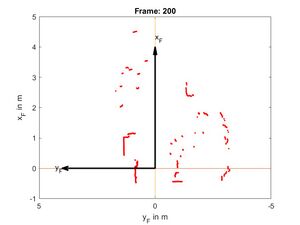
Notwendige Datei: LiDAR.mat
Nützliche Befehle: load, plot(x,y,'r.'), hold on, subplot, get, line, xlabel, ylabel
| Musterlösung 10.4 |
| Die Lösung wird in der Übung besprochen. |
Übung 10.5: KOS-Trafo: Homogene transformationsmatrix, Inverse Transformation
Mit einem LiDAR Sensor wird die Fahrt eines Roboters vermessen. Als digitale Karte liegen die Punkte des äußeren und inneren Fahrbahnrandes vor.
Aufgaben:
- Zeichnen
Gegeben sind:
- m: Ursprung des W-KOS im T-KOS in m
- m: Punkt der Startlinie im T-KOS in m
- m: Startpunkt des AMR im T-KOS in m
- m: Objektposition im T-KOS in m
Notwendige Dateien:
| Vorlage 10.5 |
%% Fahrbahnmarkierungen
load('InnenLinie.mat')
load('AussenLinie.mat')
%% Gegeben
T_r_OW = [-4.7710;4.5473;0.03;1] % Ursprung des W-KOS im T-KOS in m
T_r_S = [-4.1584;2.8208;0.03;1] % Punkt der Startlinie im T-KOS in m
T_r_AMR = [-3.9137;2.7293;0.03;1] % Startpunkt des AMR im T-KOS in m
T_r_O = [-1.8647;-1.8491;0.03;1] % Objektposition im T-KOS in m
|
| Musterlösung 10.5 |
| Die Lösung wird in der Übung besprochen. |
→ zurück zum Hauptartikel: BSE Signalverarbeitende Systeme
→ weiter zum Artikel: Signalverarbeitende Systeme - SoSe25