Zeit-, Entfernungs- und Gewichtsschätzung: Unterschied zwischen den Versionen

Version vom 11. Dezember 2024, 13:10 Uhr

→ zurück zur Übersicht: WS 24/25: Escape Game

Autoren:	Niklas Reeker, Oliver Scholze und Johann Kismann
Betreuer:	Marc Ebmeyer

Abb. 01: Skizze des Projekts Zeitschätzung

Einleitung

Bereits im Grundschulalter versuchen wir Kindern ein Gefühl für Zeit zu vermitteln. Indem sie Zeitintervalle schätzen und dabei oft feststellen, wie sehr sie danebenliegen können, erkennen sie die Bedeutung von Zeit und beginnen Uhren zu tragen. Als Erwachsene haben wir zwar ein besseres Zeitgefühl entwickelt, doch die genaue Schätzung von Zeit und Entfernungen bleibt eine Herausforderung.

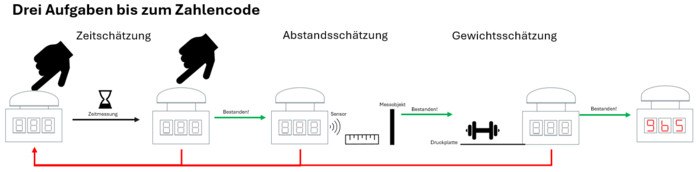
Unser Escape Game greift diese Phänomene auf spannende Weise auf. Die Aufgabe klingt einfach, erweist sich jedoch als knifflig: Halten Sie Ihren Finger genau 10 Sekunden lang auf einen Knopf – ohne Hilfsmittel zur Zeitmessung. Sobald diese erste Aufgabe erfolgreich abgeschlossen ist, müssen Sie zusätzlich eine Entfernung von 10 cm abschätzen. Zur Entfernungsmessung wird ein IR-Sensor verwendet, der die Genauigkeit der Schätzung ermittelt. Eine LED über dem IR-Sensor beginnt zu blinken, um anzuzeigen, dass die Entfernung nun geschätzt werden soll. Sobald Sie glauben, die richtige Entfernung gefunden zu haben, müssen Sie erneut den Knopf drücken, um Ihre Schätzung zu bestätigen. Ist diese Aufgabe korrekt gemeistert, erleuchtet die nächste LED über dem Drucksensor und es muss das dritte und damit auch das letzte Rätsel gelöst werden. Dies umfasst eine Gewichtsschätzung über einen Drucksensor. Dabei muss bei einer Auswahl von drei verschiedenen Gewichten (50 g/100 g/150 g) das Gewicht mit 100 g ausgewählt und auf den Drucksensor gestellt werden. Auch hier stellt ein erneuter Knopfdruck die Bestätigung der Auswahl dar.

Lassen Sie den Knopf zu früh oder zu spät los, schätzen Sie die Entfernung falsch oder wählen Sie das falsche Gewicht, ertönt eine traurige Melodie und die tatsächlich gedrückte Zeit, die geschätzte Entfernung oder das ausgewählte Gewicht werden angezeigt. So erfahren Sie genau, wie weit Sie von den Zielwerten entfernt waren und ob Ihre Schätzungen zu kurz oder zu lang waren. Treffen Sie jedoch die richtigen Werte, werden Sie mit einer Siegermelodie belohnt, und der Code für das Schloss erscheint auf dem Display. Nur mit diesem Code können Sie das Escape-Schloss öffnen und erfolgreich entkommen. Wichtig: Es wird immer erst die, dann die Entfernung und anschließend das Gewicht geschätzt. Ist eine der drei Schätzungen falsch, müssen Sie von vorne beginnen, beginnend mit der Zeitmessung.

Dieses Spiel verbindet Spaß und Spannung und zeigt auf unterhaltsame Weise, wie herausfordernd es sein kann, sowohl Zeit als auch Entfernungen präzise einzuschätzen. Stellen Sie Ihr Gefühl auf die Probe und finden Sie heraus, ob Sie den Code knacken können!

Anforderungen

Im nachfolgenden werden die testbaren Anforderungen gezeigt welche den korrekten Betrieb der Zeit-, Entfernungs- und Gewichtsschätzung sicherstellen und hier hinterlegt sind.

Tabelle 1: Anforderungen an das Escape Game
ID	Inhalt	Prio	Ersteller	Datum	Geprüft von	Datum	Umsetzung der Anforderung in %; Prüfer
1	Das Escape Game muss in 4-5 Minuten lösbar sein	Mittel	Niklas Reeker	02.10.2024	Oliver Scholze	02.10.2024
2	Der Spieler muss den Button für 10 Sekunden +-1 s Sekunde gedrückt halten um zum zweiten Rätsel der Abstandsmessung zu gelangen.	Hoch	Niklas Reeker	02.10.2024	Oliver Scholze	02.10.2024
3	Wenn die Zeit falsch geschätzt wurde, wird die tatsächlich gedrückte Zeit auf dem Display angezeigt.	Hoch	Niklas Reeker	02.10.2024	Oliver Scholze	02.10.2024
4	Wenn die Zeit falsch geschätzt wurde, beginnt das Spiel von vorne.	Hoch	Niklas Reeker	02.10.2024	Oliver Scholze	02.10.2024
5	Wenn die Zeit falsch geschätzt wurde, wird eine traurige Melodie abgespielt.	Mittel	Niklas Reeker	02.10.2024	Oliver Scholze	02.10.2024
6	Ist die Zeit richtig geschätzt, blinkt eine LED, alle 500 ms, bei der Entfernungsschätzung, um dem Benutzer zu zeigen wo es weitergeht.	Hoch	Niklas Reeker	02.10.2024	Oliver Scholze	02.10.2024
7	Ist die Zeit richtig geschätzt, beginnt die Entfernungsschätzung von 10 cm +-1 cm.	Hoch	Niklas Reeker	02.10.2024	Oliver Scholze	02.10.2024
8	Wenn die Entfernung falsch geschätzt wird, beginnt das Spiel von vorne mit der Zeitmessung.	Hoch	Niklas Reeker	02.10.2024	Oliver Scholze	02.10.2024
9	Wenn die Entfernung falsch geschätzt wird, wird die tatsächlich geschätzte Entfernung auf dem Bildschirm in cm angezeigt.	Hoch	Niklas Reeker	02.10.2024	Oliver Scholze	02.10.2024
10	Wenn die Entfernung falsch geschätzt wird, wird eine traurige Melodie abgespielt.	Mittel	Niklas Reeker	02.10.2024	Oliver Scholze	02.10.2024
11	Ist die Entfernung richtig geschätzt, blinkt eine LED, alle 500 ms, bei der Gewichtsschätzung, um dem Benutzer zu zeigen wo es weitergeht.	Hoch	Johann Kismann	11.10.2024	Oliver Scholze	11.10.2024
12	Ist die Entfernung richtig geschätzt, beginnt die Gewichtsschätzung von 100 g +-10%.	Hoch	Johann Kismann	11.10.2024	Oliver Scholze	11.10.2024
13	Wenn das Gewicht falsch geschätzt wird, beginnt das Spiel von vorne mit der Zeitmessung.	Hoch	Johann Kismann	11.10.2024	Oliver Scholze	11.10.2024
14	Wenn das Gewicht falsch geschätzt wird, wird das tatsächliche Gewicht auf dem Bildschirm in g angezeigt.	Hoch	Johann Kismann	11.10.2024	Oliver Scholze	11.10.2024
15	Wenn das Gewicht falsch geschätzt wird, wird eine traurige Melodie abgespielt.	Mittel	Johann Kismann	11.10.2024	Oliver Scholze	11.10.2024
16	Bei richtiger Zeitschätzung wird eine Siegesmelodie abgespielt.	Mittel	Niklas Reeker	02.10.2024	Oliver Scholze	02.10.2024
17	Bei richtiger Entfernungsschätzung wird eine Siegesmelodie abgespielt.	Mittel	Niklas Reeker	02.10.2024	Oliver Scholze	02.10.2024
18	Bei richtiger Gewichtsschätzung wird eine Siegesmelodie abgespielt.	Mittel	Johann Kismann	11.10.2024	Oliver Scholze	11.10.2024
19	Die Zeitmessung wird bei der Ausgabe auf ganze Sekunden gerundet (Bsp: 12,6 s entspricht 13 s).	Hoch	Niklas Reeker	02.10.2024	Oliver Scholze	02.10.2024
20	Die Entfernungsmessung wird bei der Ausgabe auf ganze Entfernungen in cm gerundet (Bsp: 12,6 cm entspricht 13 cm).	Hoch	Niklas Reeker	02.10.2024	Oliver Scholze	02.10.2024
21	Die Gewichtsmessung wird bei der Ausgabe auf ein ganzzahliges Gewicht in g gerundet (Bsp: 105,2 g entspricht 105 g).	Hoch	Johann Kismann	11.10.2024	Oliver Scholze	11.10.2024
22	Bei richtiger Gewichtsschätzung wird der dreistellige Code für das Schloss auf dem Display ausgegeben.	Hoch	Niklas Reeker	02.10.2024	Oliver Scholze	02.10.2024
23	Das Spiel muss ohne visuelle Hilfsmittel zur Zeit-, Entfernungs- und Gewichtsmessung (wie Uhren, Lineale oder Waagen) funktionieren.	Hoch	Niklas Reeker	02.10.2024	Oliver Scholze	02.10.2024
24	Die Interaktion erfolgt über einen einfachen Knopf und einen Display für Rückmeldungen.	Mittel	Niklas Reeker	02.10.2024	Oliver Scholze	02.10.2024
25	Das System muss benutzerfreundlich und für Kinder wie Erwachsene geeignet sein.	Mittel	Niklas Reeker	02.10.2024	Oliver Scholze	02.10.2024
26	Das Arduino-System wird über Simulink gesteuert.	Hoch	Niklas Reeker	02.10.2024	Oliver Scholze	02.10.2024	100
27	Das Escape Game muss in einen Schuhkarton passen.	Gering	Niklas Reeker	02.10.2024	Oliver Scholze	02.10.2024	100; Oliver Scholze

Funktionaler Systementwurf/Technischer Systementwurf

Funktionaler Systementwurf

Das Eingabegerät wird durch den/die Spieler/in aktiviert, wie in Abbildung 02 dargestellt, woraufhin die Zeitmessung beginnt. Die Aufgabe für den/die Spieler/in besteht darin, das Gerät für eine vorgegebene Dauer zu bedienen, basierend auf der Einschätzung, wann die geforderte Zeit erreicht wurde.

Sobald diese Zeitspanne erfolgreich eingehalten wurde, wird der/die Spieler/in aufgefordert, eine Entfernung von 10 cm +-1 cm zu schätzen. Ist auch diese Aufgabe korrekt absolviert, wird der/die Spieler/in aufgefordert, ein Gewicht von 100 g zu schätzen. Alle drei Schätzungen dürfen jedoch nur ohne Hilfsmittel bestimmt werden. Erst wenn alle drei Aufgaben – Zeit-, Entfernungs- und Gewichtsschätzung – korrekt abgeschlossen wurden, erhält der/die Spieler/in einen Code, der es ermöglicht, mit dem nächsten Escape-Spiel fortzufahren.

Sollten die Zeitvorgabe, die Entfernung oder das Gewicht nicht korrekt geschätzt werden, ist es erforderlich, den Vorgang zu wiederholen, beginnend mit der Zeitmessung, bis alle drei Herausforderungen erfolgreich gemeistert wurden.

Technischer Systementwurf

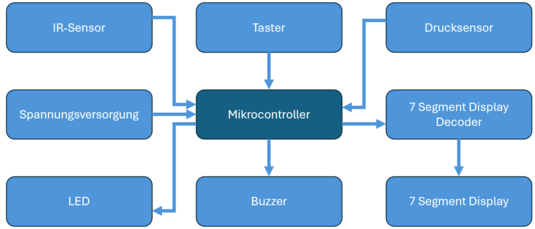
Die Steuerung und Überwachung des gesamten Spielablaufs obliegt einem Mikrocontroller, wie im funktionalen Systementwurf unter Abbildung 03 ersichtlich ist. Dieser ist direkt an die Spannungsversorgung angeschlossen, um eine kontinuierliche Funktionstüchtigkeit zu gewährleisten. Das Eingabegerät für den/die Spieler/in wird über einen Taster realisiert, der unmittelbar mit dem Mikrocontroller verbunden ist. Bei Aktivierung des Tasters initiiert dieser den Start der Stoppuhrfunktion im Mikrocontroller, um die Zeitmessung zu beginnen.

Nach erfolgreicher Zeitmessung wird der/die Spieler/in aufgefordert, eine Entfernung von 10 cm +-1 cm zu schätzen. Zur Entfernungsmessung wird ein IR-Sensor verwendet, der ebenfalls direkt mit dem Mikrocontroller verbunden ist. Um dem/der Spieler/in anzuzeigen, dass die Entfernungsmessung erfolgen soll, beginnt eine LED über dem IR-Sensor zu blinken. Diese LED ist ebenfalls an den Mikrocontroller angeschlossen und sorgt für eine visuelle Rückmeldung, wann der nächste Schritt – die Entfernungsschätzung – erfolgen muss. Für die Gewichtsschätzung wird ein Drucksensor verwendet. Ist die Entfernungsschätzung korrekt, soll eine weitere LED über dem Drucksensor für die Gewichtsschätzung blinken. Auch hierbei soll die LED als eine visuelle Rückmeldung fungieren, um den nächsten Schritt anzuzeigen.

Um das Spielergebnis – sei es die gemessene Zeit, die geschätzte Entfernung, das geschätzte Gewicht oder der freizuschaltende Code, abhängig vom Erfolg des/der Spieler/s – adäquat darzustellen, werden drei 7-Segment-Displays verwendet. Vor diesen Displays wird ein 7-Segment-Decoder geschaltet, um die Anzahl der notwendigen Verbindungen zum Mikrocontroller möglichst gering zu halten und so die Effizienz des Systems zu optimieren.

Zusätzlich wird ein Buzzer in das System integriert, um eine auditive Rückmeldung in Form einer Melodie zu ermöglichen, wie in der Einleitung beschrieben. Dieses Element trägt zur interaktiven und ansprechenden Gestaltung des Spielerlebnisses bei, indem es den/die Spieler/in sowohl bei Erfolg als auch bei Misserfolg über den Spielstatus informiert.

Materialliste

Die Materialliste gibt einen Überblick der benötigten Komponenten. Zusätzlich wird der Bestellstatus festgehalten.

Tabelle 2: Materialliste
Nr.	Anz.	Beschreibung
1	1	Funduino Arduino Mega
2	1	Taster
3	3	7-Segment-Display
4	1	(Lochrasterplatine)
5	1	Verbindungskabel
6	3	7-Segment-Decoder
7	1	Summer
8	2	LED grün
9	2	Widerstand 10kOhm
10	1	Netzteil + Kabel
11	1	Gehäuse 3D-Druck
12	2	Widerstand 150Ohm
13	1	IR-Sensor
14	1	Drucksensor

Komponentenspezifikation

Stückliste (BOM)

Die Bill of Materials befindet sich in der Dokumentation, diese ist in der Zusammenfassung hinterlegt.

Da alle weiteren Komponenten bei Reichelt bestellt werden können fallen dafür einmalig Versandkosten von 5,95€ an.

Tabelle 3: BOM
ID	Anzahl	Kosten pro Stück €	Summe	Bezeichnung / Komponente	technische Bezeichnung	Beschreibung	Datenblatt	Abbildung
1	1x	19,30€	19,30€	Arduino Mega	ARD MEGA2560 R3 Arduino kompatibles Mega 2560 R3 Board	Der Mirkocontroller mit dem ATmega2560 verfügt über 54digitale I/O - Schnittstellen. Des weiteren sind 16 analoge Eingänge die die Verarbeitung analoger Signale vorhanden.	ARD MEGA2560 R3 Arduino kompatibles Mega 2560 R3 Board	Abb. 04: Arduino Mega
2	1x	11,56€	11,56€ + 4,95€ Versand	Taster	Pilztaster Not-Aus Pilz Taster IP65	Der Taster kann mit bis zu 24V belastet werden.	Datenblatt Taster	Abb. 05: Taster
3	3x	0,99€	2,97€	7 Segment Display	Single-7-Segment-Anzeige, rot, 14,2mm, 6,4 mcd, gem. Anode	Ein 7-Segment-Display stellt eine elektronische Anzeigevorrichtung dar, die primär für die Visualisierung numerischer Daten verwendet wird.	7 Segment Display	Abb. 06: 7 Segment Display
4	3x	0,84€	2,52€	BCD-to-7-Segment-Decoder	CD 74HC4511E TEX Latch, 7-Segment, 2 ... 6 V, DIL-16	Ein 7-Segment-Decoder ist ein digitales Logikschaltkreis-Element, das digitale Eingangssignale in eine entsprechende 7-Segment-Anzeige umwandelt und die Anzahl der Anschlüsse von 7 Segment anzeigen auf die hälfte Reduzieren.	BCD-to-7-Segment-Decoder	Abb. 07: 7 Segment Decoder
5	2x	0,07€	0,14€	Pullup Widerstand 10kOhm	METALL 2,10K Widerstand, Metallschicht, 2,10 kOhm, 0207, 0,6 W, 1%	Der Pullup-Widerstand dient dazu den Eingang am Arduino auf einem definierten Wert zu halten und somit ein eindeutiges Zustand zu gewährleisten.	Pullup Widerstand 10kOhm	Abb. 08: Widerstand
6	1x	1,50€	1,50€	Summer	CMI-1295-0585T Buzzer, 85dB, 2300 Hz, 5 V	Ein Summer wandelt elektrische in akustische Signale um, indem er bei Anlegung einer Spannung zu vibrieren beginnt und so Töne erzeugt.	Summer	Abb. 09: Summer
7	2x	0,08€	0,16€	LED Grün	EVL 333-2SYGT/S5 LED, 5 mm, bedrahtet, grün, 400 mcd, 10°	Die LED hat eine Vorwärtsspannung von 2 V und darf bei maximal 20mA betrieben werden.	LED	Abb. 10: LED
8	2x	0,07€	0,14€	Widerstand 150Ohm	METALL 150 Widerstand, Metallschicht, 150 Ohm, 0207, 0,6 W, 1%	Der Widerstand dient als Vorwiderstand der LEDs.	Widerstand 150Ohm	Abb. 08: Widerstand
9	1x	5,15€	5,15€	Drucksensor	ARD SEN PRESSURE Arduino - Drucksensor, 20 g bis 10 kg	Der Drucksensor ist in der Lage, Gewichte im Bereich von 0 bis 10 kg zu erfassen und gibt in Abhängigkeit vom gemessenen Gewicht ein analoges Signal im Bereich von 0 bis 5 Volt aus.	Drucksensor	Abb. 11: Drucksensor
10	1x	32,95 €	32,95 €	IR-Sensor	IR Abstandssensor, 40- 300mm, analog, inkl. Kabel	Der GP2Y0A21YK0F-K Distanzsensor misst Entfernungen im Bereich von 40 mm bis 300 mm und gibt ein analoges Ausgangssignal proportional zur erfassten Distanz aus. Das Signal kann direkt zur weiteren Verarbeitung genutzt werden. Der Sensor wird mit einem Kabel geliefert, das eine einfache Integration ermöglicht.	IR-Sensor	Abb. 12: SHARP IR GP2Y0A41SK0F
10	1x	9,20€	9,20€	Steckernetzteil 9V für ARD Mega	HNP 18-090V2 Steckernetzteil, 18 W, 9 V, 2 A	18 W Steckerschaltnetzteil mit Universaleingang 90 - 264 V AC für Spannungsversorgung des ARD Mega.	Steckernetzteil	Abb. 13: Steckernetzteil

Technische Daten der Sensoren

Die technischen Daten (Tabelle 4) der Sensoren geben Aufschluss über den Einsatzbereich und die Anforderungen, die erfüllt werden müssen, um diese in die Messumgebung zu integrieren.

Tabelle 4: Technische Daten der Sensoren
	GP2Y0A41SK0F	ARD SENPRESSURE
Messbereich	4 - 30 cm	0 - 10 kg
Versorgungsspannung	4.5 V - 5.5 V	3,3 V - 5 V
Versorgungsstrom	typ. 12 mA	-
Genauigkeit	-	+-2,5%
Arbeitstemperatur	-10 °C - +60 °C	-20 °C - +60 °C

In Tabelle 5 wird die Pinbelegung der Sensoren erläutert, wobei beide Sensoren über drei Pins verfügen, die die Stromversorgung, den analogen Ausgang und die Erdung bereitstellen.

Tabelle 5: Pinbelegung der Sensoren
	GP2Y0A41SK0F	ARD SENPRESSURE
Pin 1	Versorgungsspannung VCC; 5 V	Versorgungsspannung VCC; 5 V
Pin 2	Analoger Ausgang; 0 V .. 5 V	Analoger Ausgang; 0 V .. 5 V
Pin 3	Masse (GND); 0 V	Masse (GND); 0 V

Funktionsweise und Kalibrierung der Sensoren

Drucksensor

Der ARD SEN PRESSURE Drucksensor für Arduino funktioniert auf Basis piezoresistiver Technologie, was bedeutet, dass er Druckkräfte über eine Widerstandsänderung misst und in ein elektrisches Signal umwandelt. Wenn eine Kraft auf den Sensor ausgeübt wird, verformt sich ein empfindliches Material im Inneren des Sensors, was zu einer Änderung des elektrischen Widerstands führt. Dieser Widerstand variiert also direkt in Abhängigkeit von der aufgebrachten Kraft.

Diese Widerstandsänderung erzeugt ein elektrisches Signal, das als analoge Spannung ausgegeben wird. Die Spannung ist proportional zur Kraft, die auf den Sensor wirkt. Je höher der ausgeübte Druck, desto stärker verändert sich der Widerstand und damit auch das Ausgangssignal des Sensors. Bei Verbindung des Sensors mit einem analogen Eingang eines Arduino-Boards kann dieser die analoge Spannung lesen und in einen digitalen Wert umwandeln, der die Stärke des Drucks repräsentiert.

Da der Sensor für einen Messbereich von 20 g bis 10 kg ausgelegt ist, kann die analoge Spannung durch Kalibrierung in eine konkrete Gewichtskraft umgerechnet werden. Dazu muss eine Lookup-Tabelle erstellt werden, welche die verschiedenen Spannungswerte in die entsprechenden Gewichtswerte umwandelt. Um diese Tabelle zu erstellen, müssen zu bestimmten Gewichten die entsprechenden Spannungswerte notiert werden.

Tabelle 6: Kalibrierung des Drucksensors
Gewicht in kg	Spannung in V
-	-
-	-
-	-
-	-

IR-Sensor

Optische Abstandssensoren verwenden Infrarotstrahlung, das auf ein Objekt ausgestrahlt und anschließend vom Sensor detektiert wird. Aus den empfangenen Daten berechnet der Sensor die Distanz zum Objekt (siehe Abbildung einsXX):

${\displaystyle \begin{align} \frac{I_1 - I_2}{I_1 + I_2} &= \frac{L - 2x}{L} \end{align}}$

Der IR-Abstandssensor GP2Y0A41SK0F verfügt über eine biaxiale Optik (siehe Abbildung zweiXX), bei der die optischen Achsen von Sender und Empfänger voneinander getrennt verlaufen. Diese Konfiguration verbessert die Energieübertragung und optimiert die Entfernungsbestimmung. Typischerweise befinden sich die Achsen parallel zueinander, um die Funktionalität zu maximieren [3].

Abbildung einsXX: Schematischer Aufbau und Funktionsweise eines PSD-Elements. [3]
Abbildung zweiXX: Prinzipielles Schema beim Triangulations-, Puls-, Phasen- und Frequenzmessverfahren mit biaxialer Optik [3]
Abbildung dreiXX: Typischer Verlauf einer biaxialer Optik [3]

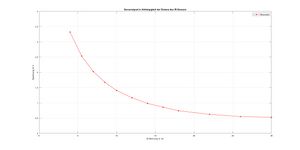
Der Abstandssensor mit einem Messbereich von 40 bis 300 mm gibt eine analoge Spannung aus, die proportional zur gemessenen Entfernung ist (siehe Abbildung dreiXX). Wenn der Abstand zum Objekt geringer ist, ist die ausgegebene Spannung höher (bei größerem Abstand ist die Spannung niedriger). Diese analoge Spannung kann an einen analogen Eingang eines Arduino-Boards angeschlossen werden. Der Arduino liest die Spannung, wandelt sie in einen digitalen Wert um und berechnet daraus die Distanz zum Objekt.

Für eine genaue Messung ist eine Kalibrierung erforderlich, da sich die analoge Spannung je nach reflektiertem Signal leicht verändern kann. Indem bekannte Abstände gemessen werden und die Spannungen erfasst wird (siehe Tabelle 7), kann eine Zuordnung erstellt werden, die dem Arduino hilft, die Spannung korrekt in eine Entfernung umzurechnen. Daraus lässt sich dann ein Lookup-Tabelle erstellen, die die Spannungswerte in die entsprechenden Entfernungen umwandelt.

Tabelle 7: Kalibrierung des IR-Sensors
Entfernung in cm	Spannung in V
4	3.319
5.5	2.535
7	2.028
8.5	1.672
10	1.408
12	1.168
14	0.9827
16	0.8602
18	0.7429
22	0.6256
26	0.5523
30	0.5327

Umsetzung HW (mechanisch)

Umsetzung HW (elektrisch)

Verdrahtungsplan und Schaltplan



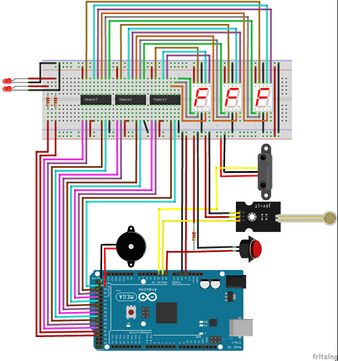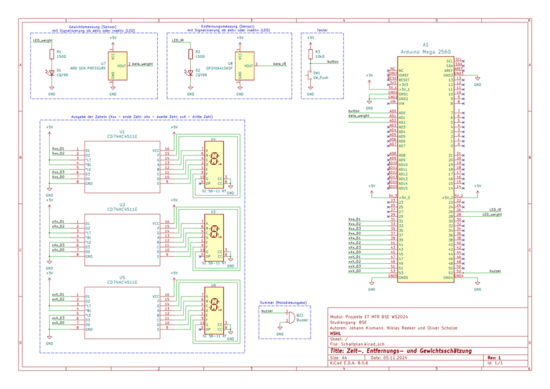Abb. 14: Verdrahtungsplan	Abb. 16: Schaltplan (mit Multisim (siehe Versionen))

In dem gezeigten Schaltplan in Abbildung 16 dienen die Netzbezeichnungen zur logischen Verbindung und Organisation der Signale zwischen verschiedenen Bauteilen. Diese Netzbezeichnungen ermöglichen es, dass elektrische Signale klar und übersichtlich an verschiedenen Stellen des Schaltplans verwendet werden können, ohne dass jede Leitung physisch durchgezeichnet werden muss. Dadurch wird der Schaltplan übersichtlicher, da wichtige Signalpfade und Verbindungen benannt und nachvollziehbar gestaltet werden. Die einzelnen Komponenten wurden zu Gruppen geordnet und mit deren Funktion beschriftet.

Anbindung des Tasters

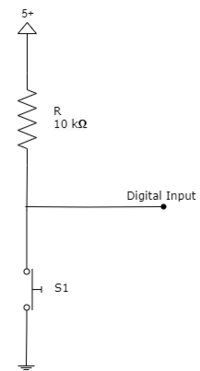
Im Schaltplan ist die Anbindung des Tasters dargestellt. Um im nicht-geschaltetem Zustand ein definiertes Potential zu gewährleisten, wird ein Pullup-Widerstand von 10 kOhm verwendet, die die Leitung auf einen logischen High-Pegel bzw. 5V ziehen. Bei Betätigung des Tasters wird die Spannung auf GND gezogen, was einen logischen LOW-Pegel am entsprechenden digitalen Pin des Arduinos Mega bewirkt, wie es in Abbildung XX dargestellt ist [2].

Berechnung der Vorwiderstände der LEDs

Um den Strom, der durch die LED fließt, zu begrenzen, wird ein Vorwiderstand benötigt. Dieser Vorwiderstand schützt die LED vor Beschädigung durch Überstrom und sorgt dafür, dass der Strom innerhalb der zulässigen Grenzen bleibt. Die Berechnung des Vorwiderstands erfolgt nach folgender Formel [1]:

$R = \frac{{U_{\text{Betrieb}} - U_f}}{{I}}$

Aus den Datenblättern des Arduino Mega und der LEDs lassen diese Werte ermitteln:

$U_{\text{Betrieb}}$ die Betriebsspannung (hier 5V),
$U_f$ die Vorwärtsspannung der LED (hier 2V),
$I$ der Strom durch die LED (hier 20 mA).

${\displaystyle R = \frac{{5V - 2V}}{{0,02A}} = \frac{{3V}}{{0,02A}} = 150\, \Omega }$

Der benötigte Vorwiderstand beträgt also 150 Ohm.

Umsetzung und Montage



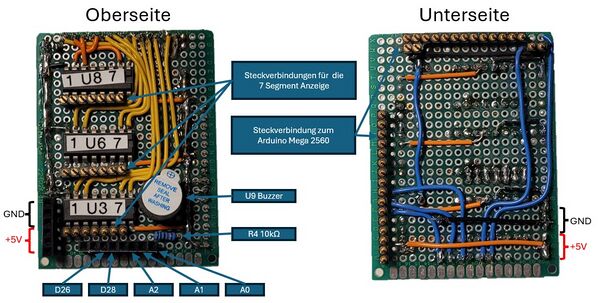
Abb. XX: Aufbau einer Adapterplatine für den Arduino Mega 2560	Abb. XX: Montage der Adapterplatine mit dem Gehäuse und den elektrischen Komponenten

In Abbildung XX wird der Aufbau der Adapterplatine gezeigt, die speziell für den Einsatz mit einem Arduino Mega 2560 und den elektrischen Komponenten des Projektes entwickelt wurde.

Oberseite der Platine:
- Die Platine verfügt über drei Decoder für die 7-Segment Anzeigen, die mit den Bezeichnungen U8, U7 und U3 gekennzeichnet sind.
- Drei Steckverbindungen sind mit jeweils 7 Pins für die 7-Segment-Anzeigen vorgesehen.
- Ein akustischer Signalgeber (Buzzer, mit der Bezeichnung U9) und der Pullup-Widerstand (R4, 10kΩ) für den Taster sind ebenfalls integriert.
- Spannungsversorgung: +5V und GND sind klar definiert und auf der Platine gekennzeichnet.
- Pinbelegung: Die Pins D26, D28, A2, A1 und A0 sind spezifisch hervorgehoben und stellen wichtige Anschlusspunkte für die Steuerung und den Signaleingang dar.

Unterseite der Platine:
- Hier sind die Lötverbindungen zu sehen, die die elektrische Verbindung zwischen den Komponenten herstellen.
- Es sind mehrere blaue und orangefarbene Leitungen sichtbar, die gezielt für die Signal- und Spannungsübertragung verlegt wurden.
- Die Spannungsleitungen (+5V und GND) sind klar gekennzeichnet, um eine korrekte Polung zu gewährleisten.

In Abbildung XX wird die Adapterplatine in einem Gehäuse montiert gezeigt:

Die Adapterplatine ist auf dem Arduino Mega 2560 aufgesteckt.
Mehrere farbige Kabel sind angeschlossen, um die Verbindung zu externen Komponenten herzustellen.
Die Verkabelung ist beschriftet, um eine einfache Identifikation der Verbindungen zu ermöglichen (z. B. A0, D26).

Umsetzung SW

Verwendete Toolbox: DSP System Toolbox, Simulink Support Package für Arduino Hardware

Zusammenspiel der Komponenten und Module



Simulink Modell	Abb. XX: PaP von der Zeit-,Entfernungs- und Gewichtsschätzung (Qualität der Darstellung musste zum Hochladen angepasst werden)(hier hinterlegt)

Umrechnung des Digitalwerts in Volt der beiden Sensoren (Drucksensor und IR-Sensor)

Im Simulink-Modell werden die analogen Sensorwerte als Digitalwert erfasst und durch ein Gain, innerhalb von Matlab Simulink, in Volt umgerechnet. Die Sensoren liefern einen 10-Bit-Digitalwert, der von 0 bis 1023 reicht und mit einer Referenzspannung von 5V arbeitet. Dieser Wert wird vom Analog-Digital-Wandler (ADC) des Arduino aufgenommen. Um den Digitalwert in Volt umzurechnen, wird folgender Berechnungsschritt durchgeführt:

$Signal in V = \frac{Digitalwert \cdot 5V}{1023}$

Der resultierende V-Wert wird anschließend gefiltert und im Modell für weitere Berechnungen verwendet.

Signalverarbeitung für den IR-Sensor (GP2Y0A41SK0F)



Abb. XX: Simulink Modell der Abstandssensorik	Abb. XX: Zusammenhang zwischen Spannung und Distanz des GP2Y0A41SK0F	Abb. XX: Signalfilterung mithilfe eines Medianfilters der Größe 30

Das analoge Ausgangssignal des Sensors wird vom Arduino am Pin 2 in ein Digitalwort umgewandelt, wie es in der Abbildung XX dargestellt ist. Dieses Digitalwort wird anschließend in eine Spannung konvertiert, wie zuvor beschrieben. Um das Signal zu glätten und Störspitzen zu eliminieren, erfolgt eine Filterung mithilfe eines Medianfilters. Im nächsten Schritt wird die gemessene Spannung mithilfe der Kalibrierung des Sensors in einen Abstand in Zentimetern umgerechnet. Die Kalibrierdaten sind in Tabelle 7 aufgeführt und in Abbildung XX grafisch dargestellt. Dieser Zusammenhang wird in Simulink durch eine 1D-Lookup-Tabelle umgesetzt, die die Zuordnung der gemessenen Spannung zur entsprechenden Distanz vornimmt.

Werte für die Lookup Table:

% Daten für die Distanz
IR_distances = [4, 5.5, 7, 8.5, 10, 12, 14, 16, 18, 22, 26, 30]; % Entfernung in cm
% Spannung für das schwarze Messobjekt
IR_voltages = [3.319, 2.535, 2.028, 1.672, 1.408, 1.168, 0.9827, 0.8602, 0.7429, 0.6256, 0.5523, 0.5327]; % Spannung in V

Anschließend erfolgt die Analyse der Messspitzen und Einsatz eines Medianfilters.

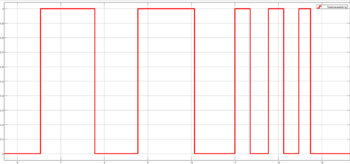
Bei der Verarbeitung der Ausgangsdaten des Infrarotsensors GP2Y0A41SK0F wurden ohne Filterung deutliche Schwankungen und zyklische Spikes festgestellt (siehe Abbildung XX). Diese resultieren aus Instabilitäten während der periodischen Berechnung und Aktualisierung des Ausgangssignals, wie in der technischen Dokumentation beschrieben. Die ungefilterten Schwankungen beeinträchtigen die Genauigkeit und Zuverlässigkeit der Messwerte, was vor allem in Anwendungen, die stabile Distanzdaten erfordern, problematisch ist.

Um diese Störungen zu minimieren, wurde ein Medianfilter implementiert:

Vorteile des Medianfilters:
- Eignet sich besonders gut zur Eliminierung von Ausreißern.
- Ignoriert extreme Abweichungen und bewahrt den zentralen Verlauf des Signals.

Filtergröße (30 Werte):
- Effektive Glättung: Reduziert Spikes und Rauschen erheblich.
- Minimale Verzögerung: Reaktionszeit bleibt für Echtzeitanwendungen akzeptabel.

Das Ergebnis zeigt, dass der Medianfilter die Spikes zuverlässig entfernt und ein robustes, geglättetes Signal erzeugt (siehe Abbildung XX).

Signalverarbeitung des Tasters



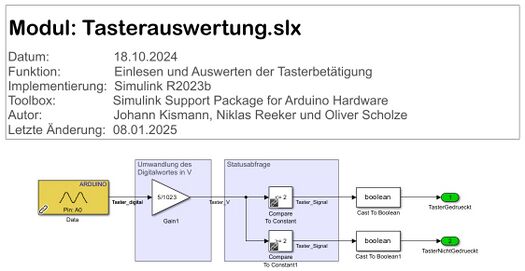
Abb. XX: Simulink Modell der Tasterauswertung	Abb. XX: Eingangssignal des Tasters mit und ohne Entprellung [2]	Abb. XX: Taster-Signal

Das vorgestellte Modell "Tasterauswertung.slx" dient der Auswertung eines mechanischen Tasters, der an einem Arduino-Mikrocontroller angeschlossen ist. Dabei wird das analoge Signal des Tasters am Pin A0 eingelesen und in eine digitale Ausgabe übersetzt. Zunächst erfolgt eine Umwandlung des digitalen Eingangswerts (Bereich 0–1023) in eine Spannung in Volt, indem das Signal mit einem Faktor von 5/1023 skaliert wird. Anschließend wird der umgerechnete Spannungswert in einer Statusabfrage mit einem Schwellenwert von 2V verglichen. Wenn der Spannungswert kleiner oder gleich 2V ist, wird ein LOW-Zustand erkannt, andernfalls ein HIGH-Zustand. Das Ergebnis wird als digitales Signal weitergegeben und kann für die Steuerung anderer Prozesse genutzt werden.

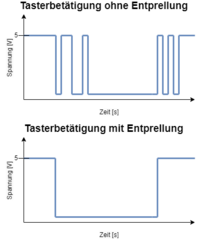
Eine zusätzliche Entprellung des Tasters ist in diesem Modell nicht implementiert, da der verwendete Taster bereits durch einen 10-kOhm-Pullup-Widerstand hardwareseitig entprellt wird. Dieser Pullup-Widerstand sorgt dafür, dass der Eingang des Mikrocontrollers im unbetätigten Zustand zuverlässig auf HIGH gezogen wird und beim Betätigen des Tasters auf LOW schaltet. Mechanische Prellvorgänge, die durch Vibrationen der Tasterkontakte entstehen können, werden durch die Stabilisierung des Signals mithilfe des Widerstands minimiert. Da die durch den Widerstand erreichte Stabilisierung ausreicht, wird das Signal bereits so geglättet, dass der Mikrocontroller keine Mehrfachimpulse registriert. Daher ist eine zusätzliche Entprellung in der Software überflüssig. Das daraus entstehende Signal des Tasters ist aus Abbildung XX zu entnehmen. Diese effiziente Hardwarelösung spart Speicherplatz und Rechenleistung, während sie gleichzeitig eine zuverlässige Funktionalität gewährleistet [2].

Signalverarbeitung des Drucksensors



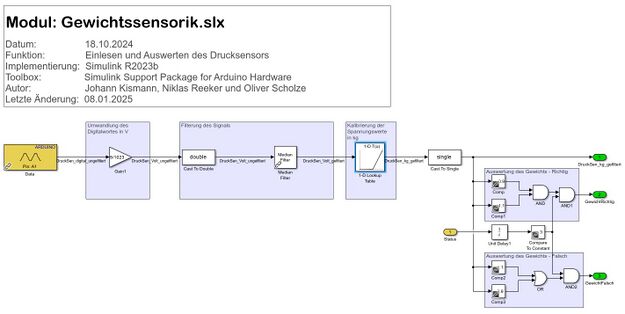Abb. XX: Simulink Modell der Gewichtsmessung

Das gezeigte Simulink-Modell dient der Verarbeitung von Drucksensor-Daten, die über einen Arduino eingelesen werden, um sie in Gewichtswerte umzuwandeln. Zunächst wird das analoge Signal des Sensors vom Arduino als digitaler Wert erfasst (0–1023). Dieser Wert wird dann mithilfe eines Gain-Blocks in eine Spannung von 0V bis 5V umgerechnet. Um Messrauschen zu reduzieren, durchläuft das Signal anschließend einen Median-Filter, der unerwünschte Störimpulse entfernt und das Signal glättet. Die gefilterte Spannung wird schließlich durch eine 1-D Lookup Table in ein Gewicht umgewandelt. Diese Tabelle weist Spannungswerten von 0V bis 5V lineare Gewichtswerte von 0 kg bis 10 kg zu, sodass eine einfache und präzise Kalibrierung erfolgt. Das resultierende Gewichtssignal ist stabil und kann weiterverwendet oder angezeigt werden.

Ansteuerung der 7-Segment-Anzeigen

Die Ansteuerung der 7-Segment-Anzeige erfolgt über einen 7-Segment-Decoder, wie den 74HC47, der in Abbildung 14 des Schaltbildes dargestellt ist. Diese Decoder sind dafür konzipiert, binäre Eingaben (BCD – Binary Coded Decimal) in Steuersignale für die sieben Segmente (1-8) der Anzeige umzuwandeln. Die genaue Zuordnung und Ansteuerung der Pins ist in Tabelle 03 aufgeführt.

Die Tabelle zeigt die Steuerung einer 7-Segment-Anzeige. Sie enthält Binärwerte (D3, D2, D1, D0), die die verschiedenen Ziffern von 0 bis 9 darstellen, und gibt an, welche Segmente (a bis g) der Anzeige aktiviert ("H" = High) oder deaktiviert ("L" = Low) sind, um die jeweilige Ziffer anzuzeigen.

D3 bis D0 sind die BCD-Eingaben (binär codierte Dezimalzahlen).
a bis g repräsentieren die Segmente der 7-Segment-Anzeige, die durch die jeweilige Kombination von High- und Low-Signalen angesteuert werden.
Die letzte Spalte „Display“ zeigt die entsprechende Zahl, die auf der Anzeige dargestellt wird.

Zum Beispiel:

Für „0“ (D3: L, D2: L, D1: L, D0: L) werden die Segmente a, b, c, d, e und f aktiviert, g bleibt deaktiviert.
Für „1“ (D3: L, D2: L, D1: L, D0: H) sind nur die Segmente b und c aktiviert.

Tabelle XX: Funktionale Tabelle zur Ansteuerung
D3	D2	D1	D0	a	b	c	d	e	f	g	Display
L	L	L	L	H	H	H	H	H	H	L	0
L	L	L	H	L	H	H	L	L	L	L	1
L	L	H	L	H	H	L	H	H	L	H	2
L	L	H	H	H	H	H	H	L	L	H	3
L	H	L	L	L	H	H	L	L	H	H	4
L	H	L	H	H	L	H	H	L	H	H	5
L	H	H	L	L	L	H	H	H	H	H	6
L	H	H	H	H	H	H	L	L	L	L	7
H	L	L	L	H	H	H	H	H	H	H	8
H	L	L	H	H	H	H	L	L	H	H	9
H	L	H	L	L	L	L	L	L	L	L	blank

Diese Tabelle wird mithilfe einer S-Funktion in Matlab-Simulink umgesetzt, dazu wird das S-Function Basic Template (sfuntmpl_basic.c) von Simulink verwendet und erweitert. Die erweiterte Funktion mit der Bezeichnung sfun_SetLogicalValueForSevenSegementDisp ließt eine Zahl ein, und separiert die einzelnen Ziffern und setzt daraufhin die Bits. Hier ist der C-Code der S-Function hinterlegt:

//%*************************************************************** *
//%                   Hochschule Hamm-Lippstadt                    *
//%*************************************************************** *
//% Modul	        : sfun_SetLogicalValueForSevenSegementDisp.c   *
//%                                                                *
//% Datum           : 18.11.2024                                   *
//%                                                                *
//% Funktion        : Drei 7-Segment-Decoder steuern und die       *
//%                   jeweiligen vier Bits setzten für das Output  *
//%                                                                *
//% Implementation  : MATLAB 2023b                                 *
//%                                                                *
//% Req. Toolbox    : -                                            *
//%                                                                *
//% Author          : Oliver Scholze, Niklas Reeker, Johann Kismann*
//%                                                                *
//% Anpassung in    : mdlInitializeSizes(SimStruct *S)             *
//%                   mdlOutputs(SimStruct *S, int_T tid)          *
//%                                                                *
//% Letzte Änderung : 18.11.2024                                   *
//%****************************************************************


/*
 * Modul: sfun_SetLogicalValueForSevenSegementDisp
 * Funktion: Vier Bits der 7-Segement-Decoder setzen 
 * Angepasste Funktionen: static void mdlInitializeSizes(SimStruct *S); 
 */


/*
 * You must specify the S_FUNCTION_NAME as the name of your S-function
 * (i.e. replace sfuntmpl_basic with the name of your S-function).
 */

#define S_FUNCTION_NAME  sfun_SetLogicalValueForSevenSegementDisp
#define S_FUNCTION_LEVEL 2

/*
 * Need to include simstruc.h for the definition of the SimStruct and
 * its associated macro definitions.
 */
#include "simstruc.h"



/* Error handling
 * --------------
 *
 * You should use the following technique to report errors encountered within
 * an S-function:
 *
 *       ssSetErrorStatus(S,"Error encountered due to ...");
 *       return;
 *
 * Note that the 2nd argument to ssSetErrorStatus must be persistent memory.
 * It cannot be a local variable. For example the following will cause
 * unpredictable errors:
 *
 *      mdlOutputs()
 *      {
 *         char msg[256];         {ILLEGAL: to fix use "static char msg[256];"}
 *         sprintf(msg,"Error due to %s", string);
 *         ssSetErrorStatus(S,msg);
 *         return;
 *      }
 *
 */

/*====================*
 * S-function methods *
 *====================*/

/* Function: mdlInitializeSizes ===============================================
 * Abstract:
 *    The sizes information is used by Simulink to determine the S-function
 *    block's characteristics (number of inputs, outputs, states, etc.).
 */
static void mdlInitializeSizes(SimStruct *S)
{
    ssSetNumSFcnParams(S, 0);  /* Number of expected parameters */
    if (ssGetNumSFcnParams(S) != ssGetSFcnParamsCount(S)) {
        /* Return if number of expected != number of actual parameters */
        return;
    }

    ssSetNumContStates(S, 0);
    ssSetNumDiscStates(S, 0);

    if (!ssSetNumInputPorts(S, 1)) return;
    ssSetInputPortWidth(S, 0, 1);
    ssSetInputPortRequiredContiguous(S, 0, true); /*direct input signal access*/
    /*
     * Set direct feedthrough flag (1=yes, 0=no).
     * A port has direct feedthrough if the input is used in either
     * the mdlOutputs or mdlGetTimeOfNextVarHit functions.
     */
    ssSetInputPortDirectFeedThrough(S, 0, 1);

    if (!ssSetNumOutputPorts(S, 12)) return;
    ssSetOutputPortWidth(S, 0, 1);
    ssSetOutputPortWidth(S, 1, 1);
    ssSetOutputPortWidth(S, 2, 1);
    ssSetOutputPortWidth(S, 3, 1);

    ssSetOutputPortWidth(S, 3, 1);
    ssSetOutputPortWidth(S, 5, 1);
    ssSetOutputPortWidth(S, 6, 1);
    ssSetOutputPortWidth(S, 7, 1);

    ssSetOutputPortWidth(S, 8, 1);
    ssSetOutputPortWidth(S, 9, 1);
    ssSetOutputPortWidth(S, 10, 1);
    ssSetOutputPortWidth(S, 11, 1);

    ssSetNumSampleTimes(S, 1);
    ssSetNumRWork(S, 0);
    ssSetNumIWork(S, 0);
    ssSetNumPWork(S, 0);
    ssSetNumModes(S, 0);
    ssSetNumNonsampledZCs(S, 0);

    /* Specify the operating point save/restore compliance to be same as a 
     * built-in block */
    ssSetOperatingPointCompliance(S, USE_DEFAULT_OPERATING_POINT);

    ssSetOptions(S, 0);
}



/* Function: mdlInitializeSampleTimes =========================================
 * Abstract:
 *    This function is used to specify the sample time(s) for your
 *    S-function. You must register the same number of sample times as
 *    specified in ssSetNumSampleTimes.
 */
static void mdlInitializeSampleTimes(SimStruct *S)
{
    ssSetSampleTime(S, 0, CONTINUOUS_SAMPLE_TIME);
    ssSetOffsetTime(S, 0, 0.0);

}



#define MDL_INITIALIZE_CONDITIONS   /* Change to #undef to remove function */
#if defined(MDL_INITIALIZE_CONDITIONS)
  /* Function: mdlInitializeConditions ========================================
   * Abstract:
   *    In this function, you should initialize the continuous and discrete
   *    states for your S-function block.  The initial states are placed
   *    in the state vector, ssGetContStates(S) or ssGetRealDiscStates(S).
   *    You can also perform any other initialization activities that your
   *    S-function may require. Note, this routine will be called at the
   *    start of simulation and if it is present in an enabled subsystem
   *    configured to reset states, it will be call when the enabled subsystem
   *    restarts execution to reset the states.
   */
  static void mdlInitializeConditions(SimStruct *S)
  {
  }
#endif /* MDL_INITIALIZE_CONDITIONS */



#define MDL_START  /* Change to #undef to remove function */
#if defined(MDL_START) 
  /* Function: mdlStart =======================================================
   * Abstract:
   *    This function is called once at start of model execution. If you
   *    have states that should be initialized once, this is the place
   *    to do it.
   */
  static void mdlStart(SimStruct *S)
  {
  }
#endif /*  MDL_START */



/* Function: mdlOutputs =======================================================
 * Abstract:
 *    In this function, you compute the outputs of your S-function
 *    block.
 */
static void mdlOutputs(SimStruct *S, int_T tid)
{
    const real_T *number = (const real_T*) ssGetInputPortSignal(S,0);

    real_T       *Xxx_D3 = ssGetOutputPortSignal(S,0);
    real_T       *Xxx_D2 = ssGetOutputPortSignal(S,1);
    real_T       *Xxx_D1 = ssGetOutputPortSignal(S,2);
    real_T       *Xxx_D0 = ssGetOutputPortSignal(S,3);

    real_T       *xXx_D3 = ssGetOutputPortSignal(S,4);
    real_T       *xXx_D2 = ssGetOutputPortSignal(S,5);
    real_T       *xXx_D1 = ssGetOutputPortSignal(S,6);
    real_T       *xXx_D0 = ssGetOutputPortSignal(S,7);

    real_T       *xxX_D3 = ssGetOutputPortSignal(S,8);
    real_T       *xxX_D2 = ssGetOutputPortSignal(S,9);
    real_T       *xxX_D1 = ssGetOutputPortSignal(S,10);
    real_T       *xxX_D0 = ssGetOutputPortSignal(S,11);

    /* Nummer in ihre Ziffern aufteilen und Gleitkommazahl zu Ganzzahl casten */
    int num_Xxx = (int)number[0] / 100;          // Erste Ziffer (Hunderterstelle)
    int num_xXx = ((int)number[0] / 10) % 10;    // Zweite Ziffer (Zehnerstelle)
    int num_xxX = (int)number[0] % 10;           // Dritte Ziffer (Einerstelle)

   /* Switch Case Anweisung für die erste Zahl Xxx */  
    switch (num_Xxx) {
        case 0:
           Xxx_D3[0] = 0;
           Xxx_D2[0] = 0;
           Xxx_D1[0] = 0;
           Xxx_D0[0] = 0;
           break;
        case 1:
           Xxx_D3[0] = 0;
           Xxx_D2[0] = 0;
           Xxx_D1[0] = 0;
           Xxx_D0[0] = 1;
           break;
        case 2:
           Xxx_D3[0] = 0;
           Xxx_D2[0] = 0;
           Xxx_D1[0] = 1;
           Xxx_D0[0] = 0;
           break;
        case 3:
           Xxx_D3[0] = 0;
           Xxx_D2[0] = 0;
           Xxx_D1[0] = 1;
           Xxx_D0[0] = 1;
           break;
        case 4:
           Xxx_D3[0] = 0;
           Xxx_D2[0] = 1;
           Xxx_D1[0] = 0;
           Xxx_D0[0] = 0;
           break;
        case 5:
           Xxx_D3[0] = 0;
           Xxx_D2[0] = 1;
           Xxx_D1[0] = 0;
           Xxx_D0[0] = 1;
           break;
        case 6:
           Xxx_D3[0] = 0;
           Xxx_D2[0] = 1;
           Xxx_D1[0] = 1;
           Xxx_D0[0] = 0;
           break;
        case 7:
           Xxx_D3[0] = 0;
           Xxx_D2[0] = 1;
           Xxx_D1[0] = 1;
           Xxx_D0[0] = 1;
           break;
        case 8:
           Xxx_D3[0] = 1;
           Xxx_D2[0] = 0;
           Xxx_D1[0] = 0;
           Xxx_D0[0] = 0;
           break;
        case 9:
           Xxx_D3[0] = 1;
           Xxx_D2[0] = 0;
           Xxx_D1[0] = 0;
           Xxx_D0[0] = 1;
           break;
       default:
           /* Bei ungültiger Zahl blank Anzeigen */
           Xxx_D3[0] = 1;
           Xxx_D2[0] = 0;
           Xxx_D1[0] = 1;
           Xxx_D0[0] = 0;
           break;}

     /* Switch Case Anweisung für die zweite Zahl xXx */                                           
     switch (num_xXx) {
        case 0:
           xXx_D3[0] = 0;
           xXx_D2[0] = 0;
           xXx_D1[0] = 0;
           xXx_D0[0] = 0;
           break;
        case 1:
           xXx_D3[0] = 0;
           xXx_D2[0] = 0;
           xXx_D1[0] = 0;
           xXx_D0[0] = 1;
           break;
        case 2:
           xXx_D3[0] = 0;
           xXx_D2[0] = 0;
           xXx_D1[0] = 1;
           xXx_D0[0] = 0;
           break;
        case 3:
           xXx_D3[0] = 0;
           xXx_D2[0] = 0;
           xXx_D1[0] = 1;
           xXx_D0[0] = 1;
           break;
        case 4:
           xXx_D3[0] = 0;
           xXx_D2[0] = 1;
           xXx_D1[0] = 0;
           xXx_D0[0] = 0;
           break;
        case 5:
           xXx_D3[0] = 0;
           xXx_D2[0] = 1;
           xXx_D1[0] = 0;
           xXx_D0[0] = 1;
           break;
        case 6:
           xXx_D3[0] = 0;
           xXx_D2[0] = 1;
           xXx_D1[0] = 1;
           xXx_D0[0] = 0;
           break;
        case 7:
           xXx_D3[0] = 0;
           xXx_D2[0] = 1;
           xXx_D1[0] = 1;
           xXx_D0[0] = 1;
           break;
        case 8:
           xXx_D3[0] = 1;
           xXx_D2[0] = 0;
           xXx_D1[0] = 0;
           xXx_D0[0] = 0;
           break;
        case 9:
           xXx_D3[0] = 1;
           xXx_D2[0] = 0;
           xXx_D1[0] = 0;
           xXx_D0[0] = 1;
           break;
       default:
           /* Bei ungültiger Zahl blank Anzeigen */
           xXx_D3[0] = 1;
           xXx_D2[0] = 0;
           xXx_D1[0] = 1;
           xXx_D0[0] = 0;
           break;}


     /* Switch Case Anweisung für die dritte Zahl xxX */                                           
     switch (num_xxX) {
        case 0: 
           xxX_D3[0] = 0;
           xxX_D2[0] = 0;
           xxX_D1[0] = 0;
           xxX_D0[0] = 0;
           break;
        case 1:
           xxX_D3[0] = 0;
           xxX_D2[0] = 0;
           xxX_D1[0] = 0;
           xxX_D0[0] = 1;
           break;
        case 2:
           xxX_D3[0] = 0;
           xxX_D2[0] = 0;
           xxX_D1[0] = 1;
           xxX_D0[0] = 0;
           break;
        case 3:
           xxX_D3[0] = 0;
           xxX_D2[0] = 0;
           xxX_D1[0] = 1;
           xxX_D0[0] = 1;
           break;
        case 4:
           xxX_D3[0] = 0;
           xxX_D2[0] = 1;
           xxX_D1[0] = 0;
           xxX_D0[0] = 0;
           break;
        case 5:
           xxX_D3[0] = 0;
           xxX_D2[0] = 1;
           xxX_D1[0] = 0;
           xxX_D0[0] = 1;
           break;
        case 6:
           xxX_D3[0] = 0;
           xxX_D2[0] = 1;
           xxX_D1[0] = 1;
           xxX_D0[0] = 0;
           break;
        case 7:
           xxX_D3[0] = 0;
           xxX_D2[0] = 1;
           xxX_D1[0] = 1;
           xxX_D0[0] = 1;
           break;
        case 8:
           xxX_D3[0] = 1;
           xxX_D2[0] = 0;
           xxX_D1[0] = 0;
           xxX_D0[0] = 0;
           break;
        case 9:
           xxX_D3[0] = 1;
           xxX_D2[0] = 0;
           xxX_D1[0] = 0;
           xxX_D0[0] = 1;
           break;
       default:
           /* Bei ungültiger Zahl blank Anzeigen */
           xxX_D3[0] = 1;
           xxX_D2[0] = 0;
           xxX_D1[0] = 1;
           xxX_D0[0] = 0;
           break;}
}



#define MDL_UPDATE  /* Change to #undef to remove function */
#if defined(MDL_UPDATE)
  /* Function: mdlUpdate ======================================================
   * Abstract:
   *    This function is called once for every major integration time step.
   *    Discrete states are typically updated here, but this function is useful
   *    for performing any tasks that should only take place once per
   *    integration step.
   */
  static void mdlUpdate(SimStruct *S, int_T tid)
  {
  }
#endif /* MDL_UPDATE */



#define MDL_DERIVATIVES  /* Change to #undef to remove function */
#if defined(MDL_DERIVATIVES)
  /* Function: mdlDerivatives =================================================
   * Abstract:
   *    In this function, you compute the S-function block's derivatives.
   *    The derivatives are placed in the derivative vector, ssGetdX(S).
   */
  static void mdlDerivatives(SimStruct *S)
  {
  }
#endif /* MDL_DERIVATIVES */



/* Function: mdlTerminate =====================================================
 * Abstract:
 *    In this function, you should perform any actions that are necessary
 *    at the termination of a simulation.  For example, if memory was
 *    allocated in mdlStart, this is the place to free it.
 */
static void mdlTerminate(SimStruct *S)
{
}


/*=============================*
 * Required S-function trailer *
 *=============================*/

#ifdef  MATLAB_MEX_FILE    /* Is this file being compiled as a MEX-file? */
#include "simulink.c"      /* MEX-file interface mechanism */
#else
#include "cg_sfun.h"       /* Code generation registration function */
#endif

Ansteuerung des Buzzer

Ansteuerung des LEDs



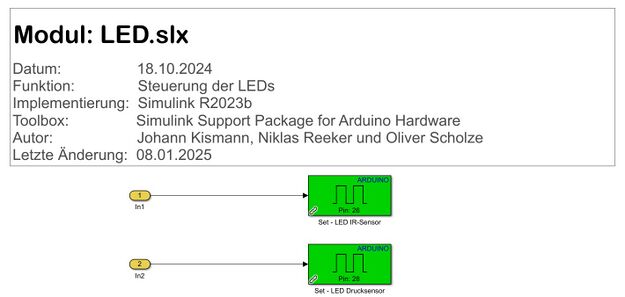Abb. XX: Simulink Modell zur Ansteuerung der LEDs

Das Diagramm zeigt die Steuerung von zwei LEDs über einen Arduino. Die Zustände `Zustand_LED_IR` und `Zustand_LED_Druck` steuern die Pins 26 und 28, die jeweils die LED des IR-Sensors und die LED des Drucksensors aktivieren.

Komponententest

In den Komponententests werden sämtliche Funktionalitäten des Projekts einzeln geprüft, um sicherzustellen, dass jede Komponente ordnungsgemäß funktioniert, bevor der Stateflow validiert werden kann. Die Tabelle XX dokumentiert die einzelnen Komponententests, einschließlich der jeweiligen Komponente, der durchgeführten Testmethoden, der erwarteten Ergebnisse sowie der gemessenen Ergebnisse. Dies ermöglicht eine umfassende Überprüfung der Funktionalität jeder Komponente.

Die Tests werden von einem Erstprüfer durchgeführt, wobei die Freigabe durch einen Zweitprüfer erfolgt. Zur besseren Nachvollziehbarkeit und Verständlichkeit des Prüfprozesses wird außerdem der Messaufbau detailliert dokumentiert.

Tabelle XX: Durchführung der Komponententest
Komponente	Durchführung	Erwartendes Ergebnis	Gemessenes Ergebnis (rot = n.i.O., grün = i.O.)	Erstprüfer	Zweitprüfer	Messaufbau
Taster	Überprüfung der Betätigungsdauer eines mechanischen Tasters und Vergleich der gemessenen Zeiten zwischen einem externen Timer und der Softwaremessung.	5s+-10%, 10s+-10%, 15s+-10%		Johann Kismann	Niklas Reeker
IR-Sensor	Überprüfung der Genauigkeit eines Infrarot-Abstandssensors durch Vergleich der gemessenen Abstände zwischen einem externen Messgerät (Lineal) und der Softwaremessung des Sensors.	8cm+-10%, 10cm+-10%, 15cm+-10%	Abb.: Auswertung des IR-Sensors 7.966cm, 10cm und 14.8cm	Oliver Scholze	Johann Kismann	Abb.: Messaufbau für den Test des IR-Sensors
Drucksensor	Überprüfung der Gewichtsmessung eines Drucksensors durch den Vergleich der gemessenen Gewichte mit externen Referenzgewichten und der Softwaremessung des Drucksensors.	50g+-10%, 150g+-10%, 200g+-10%		Niklas Reeker	Oliver Scholze
LEDs	Überprüfung der Funktionalität von LEDs in dem System, um sicherzustellen, dass sie ordnungsgemäß leuchten.	zwei LEDs leuchten	zwei LED leuchten (siehe Messaufbau)	Oliver Scholze	Johann Kismann	Abb.: Erfolgreiche Ausgabe der dreistelligen Zahl
7-Segment-Anzeigen	Überprüfung der korrekten Ausgabe einer dreistelligen Zahl durch das System, um sicherzustellen, dass die Zahl korrekt dargestellt und ohne Fehler übergeben wird.	580	Abb.: Erfolgreiche Ausgabe der dreistelligen Zahl	Oliver Scholze	Niklas Reeker	siehe Testergebnis
Ton	Überprüfung der Tonausgabe eines Buzzers, indem eine Gewinner- und eine Verlierer-Melodie abgespielt wird. Ziel ist es sicherzustellen, dass der Buzzer die Melodien korrekt und klar wiedergibt.	Melodie gewonnen und verloren		Niklas Reeker	Johann Kismann

Anschließend wird der Stateflow integriert und ein umfassender Systemtest durchgeführt, der sämtliche Funktionen beinhaltet. In diesem Zusammenhang wird die Anforderungsliste erweitert und der Erfüllungsgrad jeder Anforderung auf einer Skala von 0 bis 100 % bewertet. Dadurch können sämtliche Funktionalitäten systematisch geprüft und die Ergebnisse objektiv bewertet werden.

Ergebnis

Testauswertung
Systemverhalten
Erfüllungsgrad der Anforderungen
Defizite

Zusammenfassung

Beschreibung des Projektes
Fazit aus den Ergebnissn

Lessons Learned

Bedeutung der Planung: Eine gründliche und detaillierte Planung ist entscheidend für den Projekterfolg.
Effiziente Aufgabenteilung und Zeitmanagement: Klare Zuständigkeiten und eine realistische Zeiteinteilung wirken sich positiv auf das Endergebnis aus.
Berücksichtigung von Fertigungstoleranzen: Um Nacharbeiten zu minimieren, sollten die Toleranzen beim 3D-Druck frühzeitig berücksichtigt werden.
Optimierung durch PCB-Design mit Multisim: Der Einsatz von Multisim zur Leiterplattenentwicklung verringert den Arbeitsaufwand und erhöht die Effizienz, da umfangreiche Lötarbeiten entfallen und die Verbindungen präziser und zuverlässiger gestaltet werden können.

Projektunterlagen

Abb. XX: Gantt Projektplan für das Projekt "Zeit-, Entfernungs- und Gewichtsschätzung“

SVN-Projektdaten

Projektordner

Dokumentation
HW Elektrotechnik
1. Schaltplan
2. Fritzing Verdrahtungsplan
HW Mechanik
Software
1. Bibliotheken
2. Darstellung
3. Funktionen
4. Parameter
5. start.m
Unterlagen und Datenblätter

Projektplan

Der Projektplan in Abbildung XX zeigt den zeitlichen Ablauf eines Projekts von Oktober 2024 bis Januar 2025. Verschiedene Aufgaben sind in einem Gantt-Diagramm als Balken dargestellt, die die Start- und Enddaten visualisieren. Aufgaben wie die mechanische Vorinstallation, die Installation des Schutzhauses und Systemtests sind aufgeführt. Abhängigkeiten zwischen den Aufgaben werden durch Pfeile verdeutlicht. Das Projekt endet Anfang Januar 2025 mit der abschließenden Dokumentation und der Vorbereitung für die Projektmesse. Der Projektplan ist hier hinterlegt.

Projektdurchführung

YouTube Video

Weblinks

Literatur

[1] Elektronik Kompendium: Vorwiderstand Berechnen. URL: https://www.elektronik-kompendium.de/sites/grd/1006011.htm, 11. Oktober 2024
[2] Wührt Elektronik Kompendium: Kontakt-Entprellschaltung für Taster. URL: https://www.we-online.com/catalog/media/o185485v410%20SN015b%20DE.pdf, 25.10.2024
[3] Wiki HSHL: SHARP IR Abstandsensor GP2Y0A21YK0F. URL: https://wiki.hshl.de/wiki/index.php?title=SHARP_IR_Abstandsensor_GP2Y0A21YK0F&action=edit&section=11, 10.12.2024