Selbstfahrendes Motorad mit Arduino: Unterschied zwischen den Versionen
| Zeile 49: | Zeile 49: | ||
{| | {| | ||
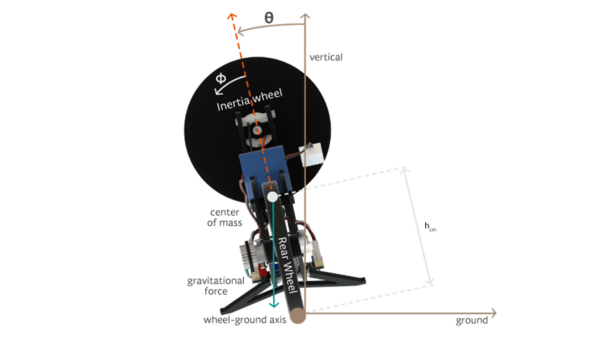
|[[Datei:Beschreibung_des_Motorrades_durch_physikalische_Größe.png|thumb|links|600px|Bild 3: Beschreibung des Motorrades durch physikalische Größe. [[Benutzer:Junjie Lyu|Junjie Lyu]] ([[Benutzer Diskussion:Junjie Lyu|Diskussion]]) 10:49, 12. Okt. 2021]] | |[[Datei:Beschreibung_des_Motorrades_durch_physikalische_Größe.png|thumb|links|600px|Bild 3: Beschreibung des Motorrades durch physikalische Größe. [[Benutzer:Junjie Lyu|Junjie Lyu]] ([[Benutzer Diskussion:Junjie Lyu|Diskussion]]) 10:49, 12. Okt. 2021]] | ||
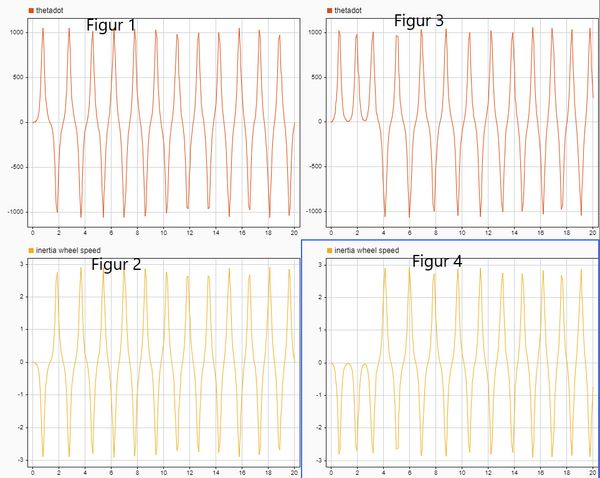
|[[Datei:Beobachtung der Regelstrecke.png| | |[[Datei:Beobachtung der Regelstrecke.png|thumb|mittens|600px|thumb|Bild 4.1: Beobachtung der Regelstrecke.[[Benutzer:Junjie Lyu|Junjie Lyu]] ([[Benutzer Diskussion:Junjie Lyu|Diskussion]]) 23:03, 22. Okt. 2021]] | ||
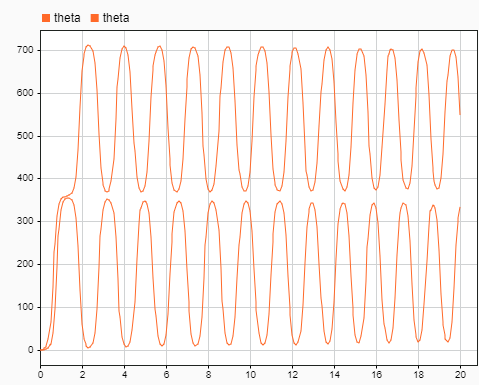
|[[Datei:Keine Regler Beobachtung Theta.png|thumb|rechts|600px|thumb|Bild 4.2: Beobachtung der Regelstrecke.[[Benutzer:Junjie Lyu|Junjie Lyu]] ([[Benutzer Diskussion:Junjie Lyu|Diskussion]]) 11:36, 23. Okt. 2021]] | |||
|} | |} | ||
| Zeile 67: | Zeile 68: | ||
|} | |} | ||
In diesem Projekt selbstfahrendes Motorrad ist die Regelstrecke der Neigungswinkel <math> \theta </math>. Beobachten Wir unter den Bedingungen ohne externe Störung und Drehmoment vom DC Motor, wie die Regelstrecke reagiert. Im Bild4 werden die Ergebnisse beschreibt. Figur 1 und Figur 2 sind die Rotationsgeschwindigkeiten von Motorrad und Trägheitrad unter den ursprünglichen Bedingungen <math> \theta_0 = 0 </math> und <math> \dot\theta_0 = 0 </math>. Figur 3 und Figur 4 sind die Rotationsgeschwindigkeiten von Motorrad und Trägheitrad unter den ursprünglichen Bedingungen <math> \theta_0 = 1 </math> und <math> \dot\theta_0 = 0 </math>. Wir können die folgende | In diesem Projekt selbstfahrendes Motorrad ist die Regelstrecke der Neigungswinkel <math> \theta </math>. Beobachten Wir unter den Bedingungen ohne externe Störung und Drehmoment vom DC Motor, wie die Regelstrecke reagiert. Im Bild4.1 und Bild4.2 werden die Ergebnisse beschreibt. Figur 1 und Figur 2 sind die Rotationsgeschwindigkeiten von Motorrad und Trägheitrad unter den ursprünglichen Bedingungen <math> \theta_0 = 0 </math> und <math> \dot\theta_0 = 0 </math>. Figur 3 und Figur 4 sind die Rotationsgeschwindigkeiten von Motorrad und Trägheitrad unter den ursprünglichen Bedingungen <math> \theta_0 = 1 </math> und <math> \dot\theta_0 = 0 </math>. Bild4.2 ist die Antwort von <math> \theta </math> unter den ursprünglichen Bedingungen <math> \theta_0 = 0 </math> und <math> \dot\theta_0 = 0 </math>. Wir können die folgende Ergebinisse bemerken: 1) Die Signals sind wegen des Gravitationsmomentes oszillierend. 2) <math> \dot\theta</math> und <math> \dot\phi </math> haben gleiche Frequenz und ähnliche Form aber invertiert. 3) Beim zweiten Durchlauf dauert es einige Zeit, bis ein stabiler Zustand erreicht wird, bei <math>\theta</math> in einen rein oszillierenden Zustand übergeht, während sich das Signal beim ersten Durchlauf direkt in diesem Zustand befindet. 4) Bei stabilem Zustand ist das Signal vom zweiten Durchlauf oszillierend im Intervall ingefähr [360 720], aber das Signal vom ersten Durchlauf im Intervall ingefähr [0 360]. In der realen Welt wird dies aufgrund des physischen Bodens nicht passieren. wir konzentrieren uns auf das Verhalten des Systems, wenn der Neigungswinkel des Motorrads nahe 0 ist. | ||
== Theoretische Diskussion über Bewegungsgleichungen für Motorrad == | == Theoretische Diskussion über Bewegungsgleichungen für Motorrad == | ||
Version vom 23. Oktober 2021, 12:54 Uhr
Autoren: Junjie Lyu
Betreuer: Prof. Schneider
Art: PA
Projektlaufzeit: 04/2021-04/2022

Thema
Aufbau eines selbsfahrenden Motorades, welches sich selbst während der Fahrt ausbalanciert.
Ziel
Das Arduino Engineering Kit ermöglicht den Aufbau dreier regelungstechnischer Herausforderungen. In diesem Projekt soll ein selbstfahrendes Motorad gebaut und programmiert werden.
Aufgabenstellung
- Einarbeitung in das Thema, auch aus regelungstechnischer Sicht
- Identifikation des Regelstrecke
- Sichtung und Test des bestehenden Bausatzes
- Aufbau des Systems (ggf. Platinenfertigung, etc.)
- Vergleichen und bewerten Sie verschiedene Regleransätze (P, PI, PID und andere).
- Modellbasierte Programmierung der Hardware via Matlab und Simulink
- Test des Segway
- Dokumentation nach wissenschaftlichem Stand
- Erstellung von Gefährdungsbeurteilung und Betriebsanweisung
Anforderung
- Wissenschaftliche Vorgehensweise (Projektplan, etc.)
- Wöchentliche Fortschrittsberichte (informativ)
- Projektvorstellung im Wiki
- Machen Sie ein tolles Videos, welches die Funktion visualisiert.
Gantt - Chart

Datei:Gantt Chart für Projektarbeit.xlsx
Die Projektarbeit einschließlich Projektseminar wird im Sommersemester 2021 angemeldet. Das heißt, die Benotung der Projektarbeit muss bis zum Ende des Wintersemesters 21/22 erfolgt sein.
Bewertung des Bausatzes
Das Motorrad ist ein zweirädrig Roboter, der mit Hilfe einer rotierenden Scheibe (Trägheitsrad) das Gleichgewicht halten und sich bewegen kann, um zu kompensieren, wenn das Motorrad das Gleichgewicht verliert. Das Motorrad wird von einem Arduino MKR1000, dem Arduino MKR Motor Carrier, einem Gleichstrommotor zum Bewegen des Hinterrads, einem Encoder, einem Gleichstrommotor zum Steuern des Trägheitsrads, einer 6-Achsen-IMU, einem Standardservomotor zum Lenken des Motorradgriffs, einem Abstandssensor (Ultraschallsensor) und einem Drehzahlmesser (Hallsensor) gesteuert. Der Hardwareaufbau konnte mithilfe der Anweisung des Anleitungsvideos zusammengebaut werden. Das Kabel vom Gleichstrommotor zum Steuern des Trägheitsrads ist nicht lang genug. Versuchen Wir, durch das Innere des Motorrads zu führen, um dem Arduino MKR Motor Carrier anzuschließen. Der Akku rutscht leicht vom Motorkörper. Versuchen wir, mit einem Gummi den Akku mit Motorkörper befestigen.
Aufbau des Systems
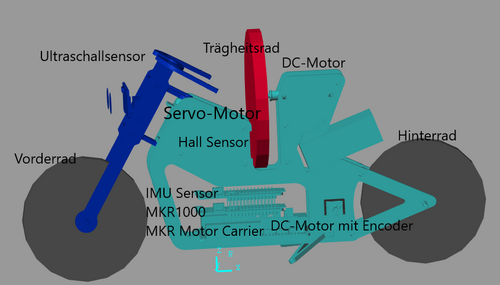
Die Komponenten sind in der Bild2 dargestellt. Die Basis dieses Projekts bildet das Arduino-Board "MKR1000". MKR Motor Carrier ist eine MKR-Zusatzplatine für "MKR1000" zur Steuerung von Servo-, Gleichstrommotoren. Außerdem erweitert MKR Motor Carrier die Fähigkeiten von MKR1000 und vereinfacht die Anschluss zur anderen Aktoren und Sensoren über ein Reihe von 3-poligen Stiftleisten. IMU Sensor enthält verschiedene Sensoren, Beschleunigungsmesser, Gyrokope und Magnetometer, in einem einzigen Gehäuse. Mit IMU Sensor, der auf dem MKR1000 sitzt, wird die vertikale Position des selbstbalancierenden Motorrad gemisst und erkannt, wenn es fällt und der Kommuniziert mit MKR1000 via 122C. Hallsensor misst die Geschwindigkeit vom Trägheitsrad. Encoder misst die Geschwindigkeit vom Motorrad. Ultraschllsensor erkannt die Hindernisse vor dem Mortorrad. Servo-Motor ändert die Fahrrichtung des Motorrades. Das Motorrad nutzt Simulink, um die Sensoren, Aktuatoren und die Bewegung zu überwachen und zu steuern.
Identifikation der Regelstrecke
 |
 |
 |
| physikalische Größe | Bedeutung |
|---|---|
| der Neigungswinkel ist 0 Grad , wenn das Motorrad vollkommen aufrecht steht, ist positiv, wenn das Motorrad von hinten gesehen gegen den Uhrzeigersinn geneigt ist, und negativ, wenn das Motorrad im Uhrzeigersinn geneigt ist. | |
| die Rotationsverschiebung des Trägheitsrads relativ zum Rest des Motorrads ist , wobei eine positive Verschiebung als gegen den Uhrzeigersinn definiert ist. | |
| Die Höhe des Massenschwerpunkts über dem Boden bei aufrechtem Motorrad ( = 0) ist definiert als |
In diesem Projekt selbstfahrendes Motorrad ist die Regelstrecke der Neigungswinkel . Beobachten Wir unter den Bedingungen ohne externe Störung und Drehmoment vom DC Motor, wie die Regelstrecke reagiert. Im Bild4.1 und Bild4.2 werden die Ergebnisse beschreibt. Figur 1 und Figur 2 sind die Rotationsgeschwindigkeiten von Motorrad und Trägheitrad unter den ursprünglichen Bedingungen und . Figur 3 und Figur 4 sind die Rotationsgeschwindigkeiten von Motorrad und Trägheitrad unter den ursprünglichen Bedingungen und . Bild4.2 ist die Antwort von unter den ursprünglichen Bedingungen und . Wir können die folgende Ergebinisse bemerken: 1) Die Signals sind wegen des Gravitationsmomentes oszillierend. 2) und haben gleiche Frequenz und ähnliche Form aber invertiert. 3) Beim zweiten Durchlauf dauert es einige Zeit, bis ein stabiler Zustand erreicht wird, bei in einen rein oszillierenden Zustand übergeht, während sich das Signal beim ersten Durchlauf direkt in diesem Zustand befindet. 4) Bei stabilem Zustand ist das Signal vom zweiten Durchlauf oszillierend im Intervall ingefähr [360 720], aber das Signal vom ersten Durchlauf im Intervall ingefähr [0 360]. In der realen Welt wird dies aufgrund des physischen Bodens nicht passieren. wir konzentrieren uns auf das Verhalten des Systems, wenn der Neigungswinkel des Motorrads nahe 0 ist.
Theoretische Diskussion über Bewegungsgleichungen für Motorrad
Das Drehmoment beim Motorrad hat 3 Hauptkomponenten, das auf das Motorrad um die Bodenachse des Rades wirkt:
Gravitationsmoment
Trägheitsmoment des Trägheitsrads
Externes Drehmoment
In dieser theoretischen Diskussion werden wir uns auf das ideale Szenario konzentrieren, bei dem . Dissipative Kräfte wie Reibung und Widerstandseffekte zwischen beweglichen Teilen . Die Neigungswinkel ist sehr klein (nur wenige Grad), gilt für .
Nettodrehmoment beim Motorrad für Bodenradachsen:
Drehmoment beim Trägheitrad für Drehachse durch die Motorwelle des Trägheitsrades:
Gravitationsmoment:
Das von der Motorwelle auf das Trägheitrad ausgeübte Drehmoment ist gleich groß und entgegengesetzt zu dem vom Trägheitrad auf die Motorwelle ausgeübten Drehmoment:
Ersetze Gleichung (4) in Gleichung (1):
Ersetze Gleichung (3) in Gleichung (5):
Ersetze Gleichung (2) in Gleichung (6):
Ersetze Gleichung in Gleichung (7):
wir programmieren den Motor so, dass er ein Drehmoment aufbringt, das proportional zum Neigungswinkel selbst ist. Das heißt: . Ersetze Gleichung in Gleichung (8):
Von (9) erhalten wir:
Wenn größer als ist, dann geht die Winkelbeschleunigung des Motorrads um die Rad-Boden-Achse in die entgegengesetzte Richtung des Neigungswinkels . Das heißt, wenn sich das Motorrad in eine Richtung neigt, wird es in die entgegengesetzte Richtung beschleunigt. Wenn sich das Motorrad auf die andere Seite des Gleichgewichtspunktes bewegt, wechselt die Winkelbeschleunigung die Richtung, um das Motorrad wieder in Richtung Gleichgewicht zu bewegen. Es handelt sich um ein stabiles Gleichgewicht, d. h., wenn das System aus der Gleichgewichtslage heraus gestört wird, stellt es sich selbst wieder ins Gleichgewicht zurück.

die Differentialgleichung (10) löst:
In der obigen Gleichung sind und Konstanten, die von den Anfangswerten von und abhängen. ist das Trägheitsmoment des Motorradsystems um die Rad-Boden-Achse. Wenn die Konstante erhöht wird, wird die Schwingungsfrequenz schneller. Wir wollen dieses Verhalten so verbessern, dass die Amplitude der Schwingungen abnimmt und sich schließlich auf einen konstanten Neigungswinkel von 0 einpendelt und das Motorradsystem stabil auf zufällige Störeinflüsse anspricht.
Bewertung verschiedener Regleransätze
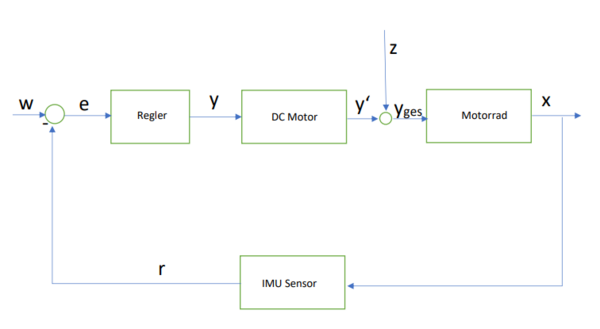
| physikalische Größe | Bedeutung |
|---|---|
| Sollwert. Wenn das Motorrad ganz aufrecht steht, ist der Neigungswinkel "0". Das heißt: | |
| Regelabweichung. Wir hoffen . Das heißt: . | |
| Stellgröße des Reglers. Unter Berücksichtigung der dynamischen Eigenschaften der Regelstrecke wird Stellgröße des Reglers nach Regelabweichung bestimmt. | |
| Stellgröße. DC motor wirkt sich auf das Trägheitsrad zur Ausgleichung der Abweichung. | |
| Störung. USB-Kabel gegen Motorräder, Luftwiderstand, Wind und verschiedene andere Ablenkungen | |
| Gesamtregelgröße. Die Gesamtregelgröße auf dem System. | |
| Istwert. Der Neigungswinkel auf dem System | |
| Rückführgröße. Die Größe des Neigungswinkels auf dem System wird von Sensoren gemisst. |
Wahl des Reglers
Simulation des Reglers
Realisierung des Reglers
Validierung des Reglers
Zusammenfassung und Ausblick
Quelltext
Video
Verlinken Sie hier ein YouTube-Video zu Ihrem fertigen Projekt. Tipps zum Video finden Sie hier.
Weblinks
- Arduino Engineering Kit
- YouTube: Unboxing the Arduino Engineering Kit
- YouTube: Motorcycle Self Balancing Using Reinforcement Learning
- YouTube: Motorcycle Maneuvers
- Arduino Store
Software
- Arduino Engineering Kit Hardware Support
- Arduino Engineering Kit Hardware Support für R2018b
- Arduino Engineering Kit Project Files
- Reinforcement learning with Self-balancing motorcycle
Siehe auch
→ zurück zum Hauptartikel: Studentische Arbeiten