Selbstfahrendes Motorad mit Arduino: Unterschied zwischen den Versionen
| Zeile 50: | Zeile 50: | ||
|+ style = "text-align: left"|Tabelle 1: Bedeutung dieser physikalischen Größe in Bild 3 | |+ style = "text-align: left"|Tabelle 1: Bedeutung dieser physikalischen Größe in Bild 3 | ||
|- | |- | ||
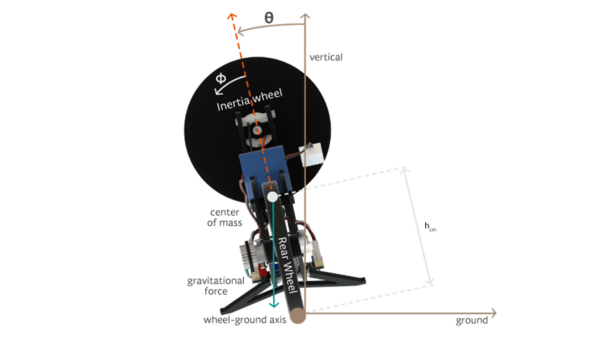
| \theta | | <math> \theta </math> | ||
| | | der Schräglagenwinkel <math> \theta </math> ist 0 Grad , wenn das Motorrad vollkommen aufrecht steht, ist positiv, wenn das Motorrad von hinten gesehen gegen den Uhrzeigersinn geneigt ist, und negativ, wenn das Motorrad im Uhrzeigersinn geneigt ist. | ||
|- | |- | ||
| | | <math> \phi </math> | ||
| die Rotationsverschiebung des Trägheitsrads relativ zum Rest des Motorrads ist <math> \phi </math>, wobei eine positive Verschiebung als gegen den Uhrzeigersinn definiert ist. | |||
|- | |- | ||
| | | <math>h_{cm} </math> | ||
| | | Die Höhe des Massenschwerpunkts über dem Boden bei aufrechtem Motorrad (<math> \theta </math> = 0) ist definiert als <math>h_{cm} </math> | ||
|} | |} | ||
Version vom 12. Oktober 2021, 12:50 Uhr
Autoren: Junjie Lyu
Betreuer: Prof. Schneider
Art: PA
Projektlaufzeit: 04/2021-04/2022

Thema
Aufbau eines selbsfahrenden Motorades, welches sich selbst während der Fahrt ausbalanciert.
Ziel
Das Arduino Engineering Kit ermöglicht den Aufbau dreier regelungstechnischer Herausforderungen. In diesem Projekt soll ein selbstfahrendes Motorad gebaut und programmiert werden.
Aufgabenstellung
- Einarbeitung in das Thema, auch aus regelungstechnischer Sicht
- Identifikation des Regelstrecke
- Sichtung und Test des bestehenden Bausatzes
- Aufbau des Systems (ggf. Platinenfertigung, etc.)
- Vergleichen und bewerten Sie verschiedene Regleransätze (P, PI, PID und andere).
- Modellbasierte Programmierung der Hardware via Matlab und Simulink
- Test des Segway
- Dokumentation nach wissenschaftlichem Stand
- Erstellung von Gefährdungsbeurteilung und Betriebsanweisung
Anforderung
- Wissenschaftliche Vorgehensweise (Projektplan, etc.)
- Wöchentliche Fortschrittsberichte (informativ)
- Projektvorstellung im Wiki
- Machen Sie ein tolles Videos, welches die Funktion visualisiert.
Gantt - Chart
Bewertung des Bausatzes
Das Motorrad ist ein zweirädrig Roboter, der mit Hilfe einer rotierenden Scheibe (Trägheitsrad) das Gleichgewicht halten und sich bewegen kann, um zu kompensieren, wenn das Motorrad das Gleichgewicht verliert. Das Motorrad wird von einem Arduino MKR1000, dem Arduino MKR Motor Carrier, einem Gleichstrommotor zum Bewegen des Hinterrads, einem Encoder, einem Gleichstrommotor zum Steuern des Trägheitsrads, einer 6-Achsen-IMU, einem Standardservomotor zum Lenken des Motorradgriffs, einem Abstandssensor (Ultraschallsensor) und einem Drehzahlmesser (Hallsensor) gesteuert. Der Hardwareaufbau konnte mithilfe der Anweisung des Anleitungsvideos zusammengebaut werden. Das Kabel vom Gleichstrommotor zum Steuern des Trägheitsrads ist nicht lang genug. Versuchen Wir, durch das Innere des Motorrads zu führen, um dem Arduino MKR Motor Carrier anzuschließen. Der Akku rutscht leicht vom Motorkörper. Versuchen wir, mit einem Gummi den Akku mit Motorkörper befestigen.
Aufbau des Systems
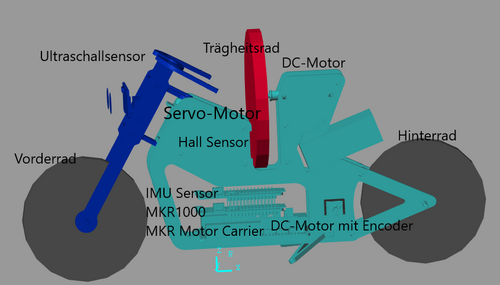
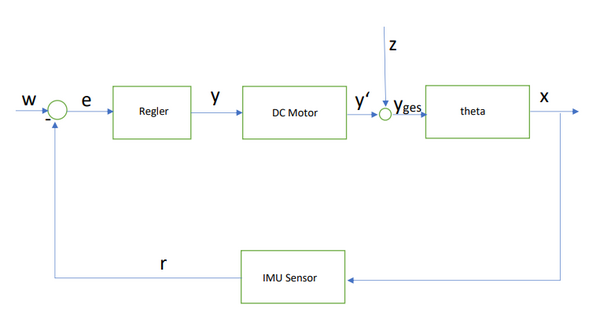
Identifikation der Regelstrecke
 |
 |
| physikalische Größe | Bedeutung |
|---|---|
| der Schräglagenwinkel ist 0 Grad , wenn das Motorrad vollkommen aufrecht steht, ist positiv, wenn das Motorrad von hinten gesehen gegen den Uhrzeigersinn geneigt ist, und negativ, wenn das Motorrad im Uhrzeigersinn geneigt ist. | |
| die Rotationsverschiebung des Trägheitsrads relativ zum Rest des Motorrads ist , wobei eine positive Verschiebung als gegen den Uhrzeigersinn definiert ist. | |
| Die Höhe des Massenschwerpunkts über dem Boden bei aufrechtem Motorrad ( = 0) ist definiert als |
Bewertung verschiedener Regleransätze
Wahl des Reglers
Simulation des Reglers
Realisierung des Reglers
Validierung des Reglers
Zusammenfassung und Ausblick
Quelltext
Video
Verlinken Sie hier ein YouTube-Video zu Ihrem fertigen Projekt. Tipps zum Video finden Sie hier.
Weblinks
- Arduino Engineering Kit
- YouTube: Unboxing the Arduino Engineering Kit
- YouTube: Motorcycle Self Balancing Using Reinforcement Learning
- YouTube: Motorcycle Maneuvers
- Arduino Store
Software
- Arduino Engineering Kit Hardware Support
- Arduino Engineering Kit Hardware Support für R2018b
- Arduino Engineering Kit Project Files
- Reinforcement learning with Self-balancing motorcycle
Siehe auch
→ zurück zum Hauptartikel: Studentische Arbeiten