Seminaraufgabe SoSe 2021: Einspurmodell Gruppe I

Autoren: Mohamed Omar Kharrat, Niclas Thon

Einleitung

In dieser Seminararbeit des Studiengangs "Business and Systems Engineering" im Modul System Design, soll ein lineares Einspurmodell anhand des V-Modells und mithilfe des Programms MATLAB / Simulink modelliert sowie simuliert werden.

Vorgehensweise nach V-Modell

Das V-Modell ist eine Vorgehensweise um Software zu entwickeln. Für diese Projektarbeit wurde diese Vorgehensweise genutzt, um abstrakte physikalische Gleichungen des Einspurmodells in Simulink zu modellieren.

Abb 1: V-Modell nach Seminaraufgabe

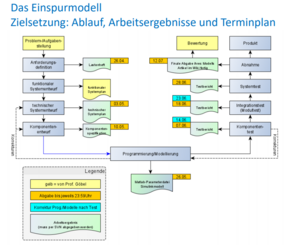
Anforderungsdefinition

Für die Anforderungen des Projektes ist ein Lastenheft erstellt worden, welches die weiteren Punkte beinhaltet.

1. Aufgabenstellung
2. Aufbau
3. Modellbeschreibung
4. Software / Werkzeuge
5. Programmierung
6. Dokumentation

Nach Abbildung 2 können die verschiedenen vorher definierten Anforderungen betrachtet werden. Diese sind für die Erfüllung der Seminaraufgabe einzuhalten.

Abb 2: Ausschnitt Lastenheft

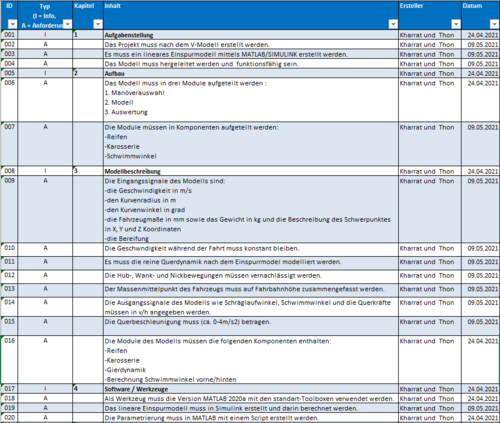
Funktionaler/Technischer Systementwurf

Der technische Systementwurf nach Abbildung 3, beschreibt die Zusammengehörigkeit der Komponenten im Modell. Dadurch ist eine bessere Übersicht gegeben, als wenn zu viele Subkomponenten verwendet werden würden. Außerdem können für dritte wichtige Parameter und Ausgänge schneller erkannt und beurteilt werden.

Abb 3: Technischer Systementwurf

Komponentenspezifikation

Für die Erstellung der Komponenten ist das Fachwissen aus zu verwenden. Daraus können die verschiedene physikalischen Zusammenhänge in den weiteren Unterpunkten in Gleichungen beschrieben werden.

• Manoeverwahl

$\delta_f = Lenkwinkel~aus~der~Parameterdatei$

Durch die Auswahl des $\delta_f$ kann der Benutzer den Lenkwinkel und die Lenkrichtung bestimmen. Außerdem ist es möglich über die Variable "manoever" eine Slalomfahrt auszuwählen.

• Eingangswerte

$KFC_x = Geschwindigkeit$

Es wird eine konstante Geschwindigkeit gewählt dadurch ist auch die Beschleunigung konstant null.

• Achsschwimmwinkel

Die folgenden Gleichungen beschreiben das Verhalten des Achsschwimmwinkels:
$l_h = l - l_v$
$\beta = \frac{-l_h}{l \cdot \delta_v}$
$\beta_v = \beta + \frac{l_v \cdot K\psi'}{KvC_x}$
$\beta_h = \beta - \frac{l_h \cdot K\psi'}{KvC_x}$

• Reifen

Für die Modellierung der Reifen sind die folgenden Gleichungen gewählt worden:
$\alpha_v = \delta_v - \beta_v$

$\alpha_h = \delta_h - \beta_h$

$RFy_v = c_v \cdot \alpha_v$

$RFy_h = c_h \cdot \alpha_h$

$RFy_h = KFy_h$

$RFy_v = KFy_v$

• Karosserie

$KFC_x = \delta_v \cdot RFy_v + \delta_h \cdot RFy_h$

$KFC_y = RFy_h + RFy_v$

$K\psi'' = \frac{(L_v \cdot KFy_v + l_h \cdot KFy_h)}{J_{zz}}$

$K\psi' = K\psi'' \cdot \frac{1}{s}$

$KaC_y = \frac{KFy_v + KFy_h}{m}$

$KaC_x = 0$

• Auswertung

Die folgenden Parameter sollen als Ausgänge im Scope der Simulation dargestellt werden:

• $KaC_y$ und $KaC_x$
  
  
• $KFC_y$ und $KFC_x$
  
  
• $\psi'$
  
  
• $\beta$, $\beta_v$ und $\beta_h$
  
  
• $\alpha_v$ und $\alpha_h$
  

Entwicklung

In diesem Abschnitt wird die Erstellung des Simulationsmodells mit Simulink anhand der vorher definierten Komponentenspezifikation erläutert.

In Abbildung 4 ist die Komponente Manöver dargestellt. In dieser wird der Fahrlenkwinkel $\delta_f$ durch die Parameterdatei eingelesen und $\delta_v$ sowie $\delta_h$ werden ausgegeben. Letzterer ist laut Spezifikation gleich null zu setzen.

Abb 4: Manöver Komponente

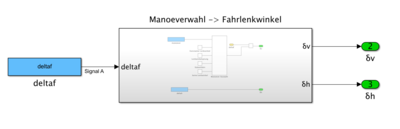
Der detaillierte Aufbau der zuvor erwähnten Komposten befindet sich in Abbildung 5. Wo durch Auswahl verschiedener Manöver, dass Lenkverhalten bestimmt werden kann.

Abb 5: Manöverauswahl

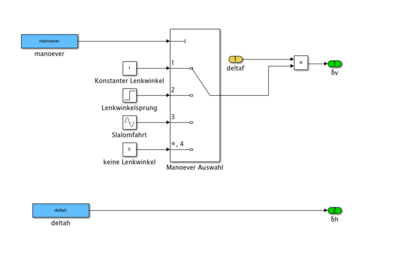
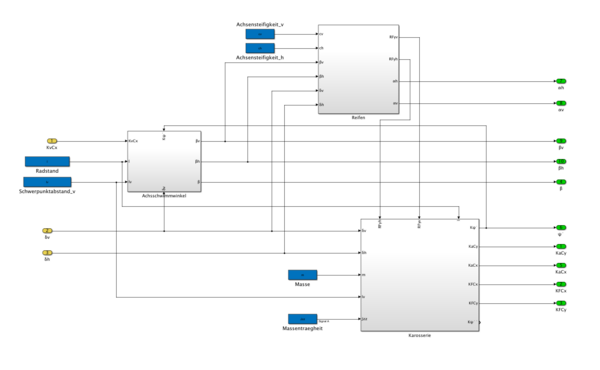
In Abbildung 6 ist das gesamte Modell dargestellt. Innerhalb der Subkomponenten Reifen, Achsschwimmwinkel und Karosserie werden die Berechnungen durchgeführt.

Abb 6: Modell

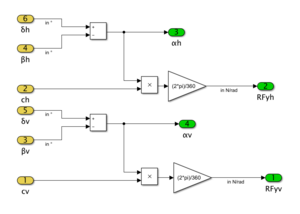
In der Komponente Reifen, kann der Zusammenhang und die Verknüpfungen der einzelnen Parameter aus der Komponentenspezifikation betrachtet werden.

Abb 7: Berechnung in der Komponente Reifen

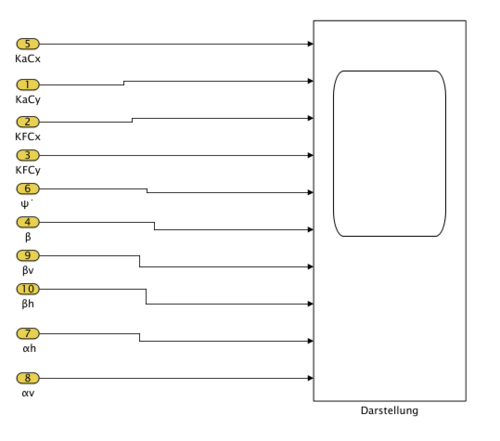
Die Ergebnisse werden in einem Scope in Simulink nach der Spezifikation dargestellt.

Abb 8: Auswertung

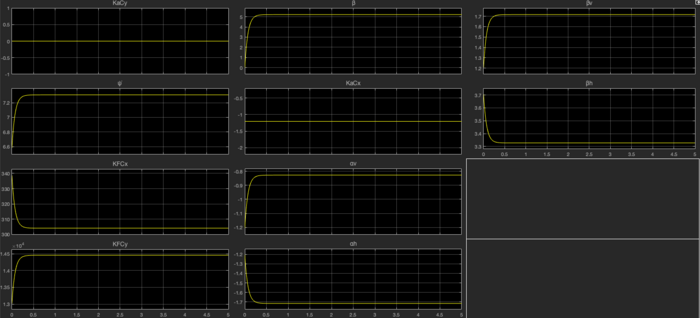
Ergebnis

Die Ergebnisse dieser Seminararbeit sowie die vollständige Ordnerstruktur des Projekts, kann unter dem folgenden Link eingesehen werden SVN.

Abb 8: Auswertung

Zusammenfassung

Für die Beurteilung der Ergebnisse dieser Seminararbeit kann gesagt werden, dass die geforderten Ausgänge dem vorgaben entsprechen. Außerdem können die geforderten Manöver nach der Anforderungsdefinition:

• Linkskurve
  
• Rechtskurve
  
• Slalomfahrt
  

mit dem Modell simuliert werden.

Ausblick

Als Ausblick dieser Arbeit, wäre eine Erstellung einer GUI für den Benutzer von weiteren Nutzen. Außerdem könnten die simulierten Werte in einer Datenbank hinterlegt werden, um eine weitere Bearbeitung der Daten vorzubereiten.