Seminaraufgabe SoSe 2021: Einspurmodell Gruppe D: Unterschied zwischen den Versionen
| Zeile 139: | Zeile 139: | ||
=== Reifen === | === Reifen === | ||
Der Achs-Schräglaufwinkel ist die Differenz aus | Der Achs-Schräglaufwinkel ist die Differenz aus Lenkwinkel und Achs-Schwimmwinkel und wird für die Vorder- und Hinterachse mit folgenden Gleichungen berechnet: | ||
<math>\alpha_v = \delta_v - \beta_v </math> | <math>\alpha_v = \delta_v - \beta_v </math> | ||
| Zeile 145: | Zeile 145: | ||
<math>\alpha_h = \delta_h - \beta_h </math> | <math>\alpha_h = \delta_h - \beta_h </math> | ||
Da im Rahmen dieser Seminaraufgabe <math>\delta_h = 0 </math> angenommen | Da im Rahmen dieser Seminaraufgabe der Lenkwinkel der Hinterachse vernachlässigt wird, wird <math>\delta_h = 0 </math> angenommen. Daraus folgt: | ||
<math>\alpha_h = - \beta_h </math> | <math>\alpha_h = - \beta_h </math> | ||
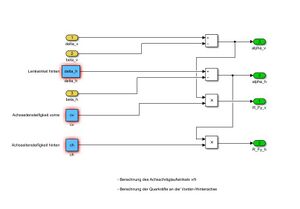
Das Produkt aus Schräglaufwinkel und Achsseitensteifigkeit ergibt die Querkräfte an den | Das Produkt aus Schräglaufwinkel und Achsseitensteifigkeit ergibt die Querkräfte an den Achsen. | ||
<math>_RF_{yv} = c_v \cdot \alpha_v</math> | <math>_RF_{yv} = c_v \cdot \alpha_v</math> | ||
| Zeile 170: | Zeile 170: | ||
<math>_K\ddot{\psi} = \frac{l_v \cdot _KF_{yv} - l_h \cdot _KF_{yh}}{J_{zz}}</math> | <math>_K\ddot{\psi} = \frac{l_v \cdot _KF_{yv} - l_h \cdot _KF_{yh}}{J_{zz}}</math> | ||
Beim linearen Einspurmodell wird von kleinen Winkeln ausgegangen. Daraus folgt für <math>_KF_{yv} _RF_{yv}</math>. | |||
Durch Integration der Gierwinkelbeschleunigung <math>_K\ddot{\psi}</math> erhält man die Gierrate <math>_K\dot{\psi}</math>. | Durch Integration der Gierwinkelbeschleunigung <math>_K\ddot{\psi}</math> erhält man die Gierrate <math>_K\dot{\psi}</math>. | ||
Version vom 12. Juli 2021, 11:56 Uhr
Autoren: Safwan Alsousou, Fabian Soldanski
Einleitung
Im Rahmen der Veranstaltung "Systems Design Engineering" im Studiengang "Business and Systems Engineering" sollen die Studierenden ein Einspurmodell nach dem V-Modell entwickeln. Dabei erfolgt die Umsetzung in Matlab-Simulink. In diesem Artikel wird das Vorgehen der Gruppe D vorgestellt.
Vorgehensweise nach dem V-Modell
Zur Komplexitätsbeherrschung wurde bei der Entwicklung des Einspurmodells nach dem V-Modell vorgegangen. Die einzelnen Abschnitte sind unten dargestellt. Der Testzweig (Punkt 6 bis 8) wurde für Gruppe H durchgeführt und wird in diesem Artikel nicht dargestellt.
- Anforderungsdefinition
- Funktionaler Systementwurf
- Technischer Systementwurf
- Komponentenspezifikation
- Programmierung/Modellierung
- Komponententest
- Integrationstest
- Systemtest
- Abnahmetest
Anforderungen
Zu Beginn der Entwicklung wurden die Anforderungen gemäß der Seminaraufgabe in einem Lastenheft zusammengefasst. Dabei wurden die Anforderungen in folgenden Kategorien eingeteilt:
- Allgemein
- Abgabe
- Meilensteine
- Aufbau
- Modul: Manöverauswahl
- Modul: Modell
- Modul: Auswertung
- Software/Werkzeuge
- Nachhaltigkeit
- Dokumentation
In Tabelle 1 sind die wichtigsten Anforderungen zusammengefasst.
| ID | Typ | Kapitel | Inhalt |
|---|---|---|---|
| 001 | A | 1 | Das Vorgehen muss nach dem V-Modell erfolgen. |
| 004 | A | 1.1 | Die Abgabe der Arbeitsergebnisse muss je Meilenstein per SVN erfolgen. |
| 016 | A | 2 | Die Betrachtung muss bei einer Fahrt mit konstanter Geschwindigkeit erfolgen. |
| 019 | A | 2 | Das Modell muss übersichtlich in folgende drei Module aufgeteilt werden:
|
| 020 | A | 2 | Innerhalb der Module muss die Aufteilung in sinnvolle Komponenten erfolgen (Reifen, Karosserie, Gierdynamik, Berechnung Schwimmwinkel vorne/hinten) |
| 030 | A | 3 | Es muss die Matlab Version 2020a mit Standard-Toolboxen verwendet werden |
Funktionaler Systementwurf/Technischer Systementwurf
Gemäß dem funktionalen Systementwurf aus der Seminaraufgabe wurde der technische Systementwurf erstellt. Der technische Systementwurf wurde in drei Module unterteilt: Manöverauswahl, Modell und Auswertung (siehe Abbildung XX). Er beinhaltet die Definition der Schnittstellen sowie die Benennung der Komponenten und deren Aufgaben.
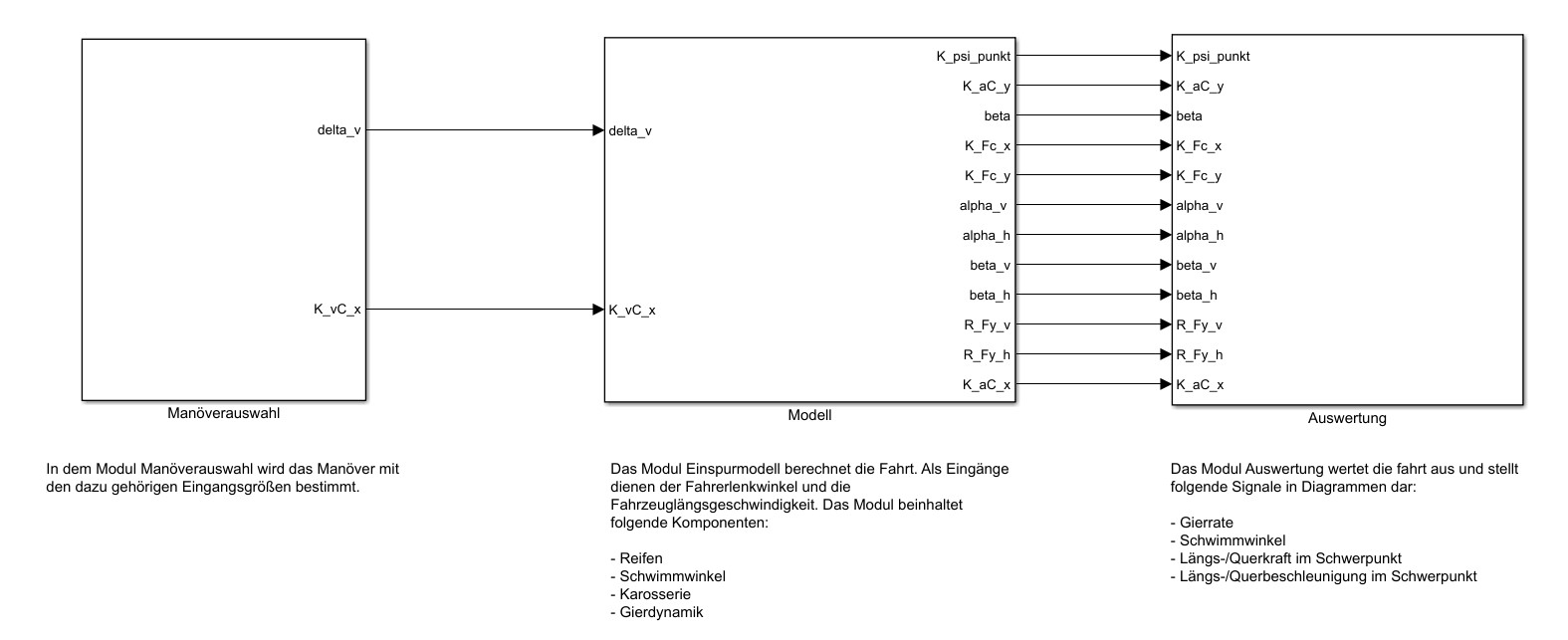
Abb. 1: Module des Simulinkmodells
Im Modul Manöverauswahl erfolgt die Wahl des spezifischen Lenkmanövers. Weiterhin werden hier die Eingangsgrößen Fahrzeuglängsgeschwindigkeit und vorderer Lenkwinkel für das Modell bestimmt. Das Modul ist in Abbildung XX dargstellt.
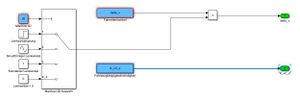
Das Modul Modell ist in vier Komponenten unterteilt: Reifen, Karosserie, Gierdynamik und Schwimmwinkel. In diesem Modul erfolgen die Berechnungen des Modells.
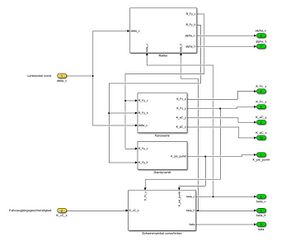
Die zur Berechnung notwendigen Parameter werden aus einem Matlab-Skript in das Modell geladen. Diese wurden der Seminaraufgabe entnommen und sind in Tabelle XX dargestellt.
| Parameter | Beschreibung | Einheit |
|---|---|---|
| Achsseitensteifigkeit vorne | ||
| Achsseitensteifigkeit hinten | ||
| Schwerpunktabstand zur Vorderachse | ||
| Radstand | ||
| Masse des Fahrzeuges | ||
| Massenträgheitsmoment |
Im Modul Auswertung werden die berechneten Signale mit Hilfe eines Scopes dargestellt (siehe Abbildung XX).
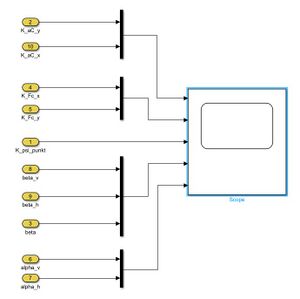
Komponentenspezifikation
Mit Hilfe der Komponentenspezifikation werden die Aufgaben, das Verhalten, der innere Aufbau sowie die Schnittstellen der einzelnen Komponenten definiert. Die Module "Manöverauswahl" und "Auswertung" beinhalten keine weiteren Unterteilungen in Komponenten. Mathematische Berechnungen werden ausschließlich in dem Modul "Modell" durchgeführt, weshalb im folgenden auf die einzelnen Komponenten dieses Moduls eingegangen wird. Die zur Berechnung verwendeten Gleichung entstammen dem Skript "Fahrwerksmanagement" von Herrn Prof. Dr.-Ing. Göbel.
Reifen
Der Achs-Schräglaufwinkel ist die Differenz aus Lenkwinkel und Achs-Schwimmwinkel und wird für die Vorder- und Hinterachse mit folgenden Gleichungen berechnet:
Da im Rahmen dieser Seminaraufgabe der Lenkwinkel der Hinterachse vernachlässigt wird, wird angenommen. Daraus folgt:
Das Produkt aus Schräglaufwinkel und Achsseitensteifigkeit ergibt die Querkräfte an den Achsen.
Karosserie
In der Komponente Karosserie werden die Kräfte und Beschleunigungen in Längs- und Querrichtung am Fahrzeugschwerpunkt berechnet.
Gierdynamik
Beim linearen Einspurmodell wird von kleinen Winkeln ausgegangen. Daraus folgt für .
Durch Integration der Gierwinkelbeschleunigung erhält man die Gierrate .
Schwimmwinkel
Programmierung/Modellierung
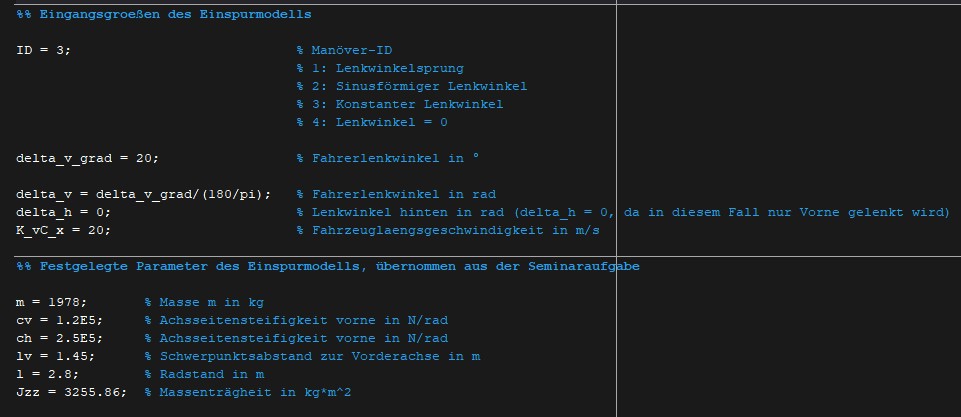
Abb. 5: Das Modul Auswertung


Ergebnis
Zusammenfassung
Arbeitsergebnisse
Literaturverzeichnis
→ zurück zum Hauptartikel: "Systems Design Engineering" - Seminaraufgabe SoSe 2021: Einspurmodell“