Seminaraufgabe SoSe 2021: Einspurmodell Gruppe B: Unterschied zwischen den Versionen

Version vom 9. Juli 2021, 13:49 Uhr

Autoren: Björn Schlottke und Dennis Schleicher

Einleitung

Dieser Artikel dokumentiert die Ausarbeitung der Gruppe B im Modul Systems Design Engineering im Sommersemester 2021. Die Aufgabe beinhaltet die Entwicklung des linearen Einspurmodells nach dem V-Modell als Tool zur Komplexitätsbeherrschung. Hierfür wurden die Inhalte des Skriptes Datei:Skript Fahrwerkmanagent ProfGöbel.pdf in Submodule und zugehörige Komponenten aufgeteilt und in einem MATLAB 2020a Simulink Modell umgesetzt.

Vorgehensweise nach V-Modell

Wie bereits erläutert wurde die Entwicklung nach dem V-Modell durchgeführt. Dies beinhaltet die in der folgenden Abbildung dargestellten Schritte. Um diese Schritte noch einmal aufzuführen, werden sie an dieser Stelle kurz aufgelistet.

Anforderungsdefinition
Funktionaler Systementwurf
Technischer Systementwurf
Komponentenspezifikation
Programmierung
Komponententest
Integrationstest
Systemtest
Abnahmetest

Die Schritte 6 - 9 werden in dem vorliegenden Artikel nicht behandelt, weil sie die Testung der Ausarbeitungen von Gruppe J sowie den Abnahmetest des entwickelten Modells durch Prof. Göbel, betreffen. Somit wird lediglich die Entwicklung des linearen Einspurmodells behandelt.

Anforderungen

Zunächst werden alle Anforderungen zu denen sich Gruppe B im Rahmen dieser Seminararbeit verpflichtet in einem Lastenheft festgehalten. Hierfür wurde das Lastenheft mit der folgenden Struktur versehen.

Formale Anforderungen
1. Nachhaltigkeit des Programmcodes
2. Abgaben des letzten Meilensteins im HSHL Wiki
Termine und Fristen
Aufbau
1. Teilmodul Mannöversteuerung
2. Teilmodul Modell
3. Teilmodul Auswertung
Modellgrundlagen

Das gesamte Lastenheft kann im SVN eingesehen werden. In Tabelle 1 wird ein Auszug aus dem Lastenheft dargestellt. Die Abkürzungen in der Spalte Typ stehen für Inhalt (= I) und Anforderung (= A).

Tabelle 1: Formale Anforderungen aus dem Lastenheft
ID	Typ	Kapitel	Inhalt
001	I	1	Formale Anforderungen
002	A		Es muss die Software MATLAB 2020a benutzt werden.
003	A		Die Vorgehensweise muss dem V-Modell nach Vorlage von Prof. Göbel entsprechen.
004	A		Es muss ein lineares Einspurmodell in MATLAB Simulink erstellt werden.
005	A		Für die Erstellung des Modells müssen die Parameter extrahiert und in MATLAB angelegt werden.
006	A		Die Parameter müssen nachträglich anpassbar sein.

Technischer Systementwurf

Im folgenden Kapitel wird der gesamte Entwurf des Systems erläutert. An dieser Stelle wird der funktionale aus dem V-Modell übergangen, da er keinen Teil der Seminaraufgabe dargestellt hat. Grundlegend ist das Simulink Modell so aufgebaut, dass es drei Submodule besitzt, welche wiederum weitere Komponenten beinhalten. Innerhalb der Komponenten ist die eigentliche Funktionalität hinterlegt. Diese Struktur wurde für die Bearbeitung der Seminaraufgabe vorgegeben und wurde ebenfalls unter den Anforderungen im Lastenheft festgehalten. Ein Abbildung die diese Struktur beinhaltet lässt sich in Abbildung 1 erkennen.

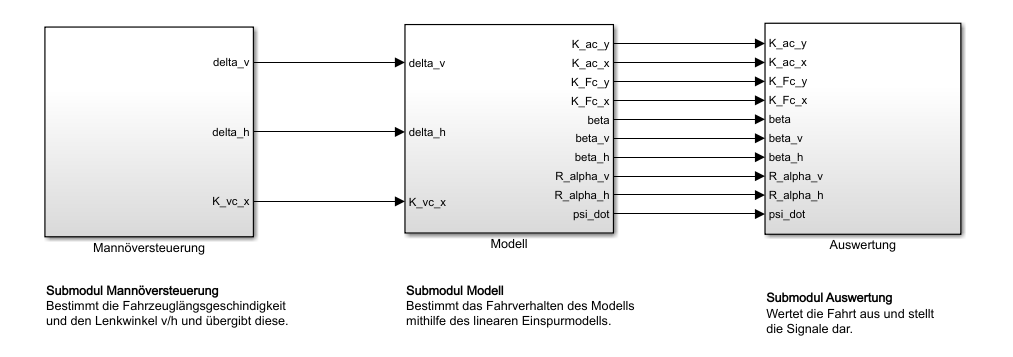
Weitergehend kann erkannt werden, dass die Submodule untereinander Verbindungen besitzen. Somit werden die folgenden Parameter zwischen den Submodulen übergeben.

Tabelle 2: Übergebene Parameter der Submodule
Parameter	Beschreibung	Einheit
$\delta_v$	Lenkwinkel vorne	$rad$
$\delta_h$	Lenkwinkel hinten	$rad$
$_Kv_{Cx}$	Fahrzeuglängsgeschwindigkeit im Fahrzeugschwerpunkt C	$\frac{m}{s}$
$_Ka_{Cy}$	Fahrzeugquerbeschleunigung im Fahrzeugschwerpunkt C	$\frac{m}{s^2}$
$_Ka_{Cx}$	Fahrzeufglängsbeschleunigung im Fahrzeugschwerpunkt C	$\frac{m}{s^2}$
$_KF_{Cy}$	Fahrzeugquerkraft im Fahrzeugschwerpunkt C	$N$
$_KF_{Cx}$	Fahrzeuglängskraft im Fahrzeugschwerpunkt C	$N$
$\beta$	Schwimmwinkel	$rad$
$\beta_v$	Schwimmwinkelanteil vorne	$rad$
$\beta_h$	Schwimmwinkelanteil hinten	$rad$
$_R\alpha_v$	Schräglaufwinkel vorne	$rad$
$_R\alpha_h$	Schräglaufwinkel hinten	$rad$

Das Submodul Mannöversteuerung besitzt nur eine Komponente, nämlich die Mannöverauswahl. Unter dem Submodul Modell befinden sich die Komponenten Reifen, Karosserie, Gierdynamik und Schwimmwinkel. Als Letztes besitzt das Submodul Auswertung keine Komponenten.

Komponentenspezifikation

Die Komponentenspezifikation definiert die Aufgabe, das Verhalten, den inneren Aufbau und die Schnittstellen der Komponenten. In den Modulen "Mannöversteuerung" und "Auswertung" werden keine Mathematischen Formeln verwendet (bei der "Mannöversteuerung" erfolgt eine Zuweisung des hinteren Lenkwinkels über eine Multiplikation mit 0, diese ist aber trivial). Das Modul "Modell" wird, wie im technischen Systemplan beschrieben, in vier Komponenten unterteilt. Deren Funktionsweise soll im Folgenden mithilfe mathematischer Zusammenhänge erläutert werden. Bei der Herleitung wurden die in ^[1] beschriebenen Formeln verwendet.

Schwimmwinkel

Die Formel der Winkelgeschwindigkeit des Schwimmwinkels wird aus dem vereinfachten Schwerpunktsatz abgeleitet. Dabei ist $_KF_{Cy}$ die im Schwerpunkt der Hinterachse angreifende Kraft, m die Fahrzeugmasse und $_K\dot{\psi}$ die Gierwinkelgeschwindigkeit.

$_K\dot{\beta} = \frac{_KF_{Cy}}{m \cdot _Kv_{Cx}} - _K\dot{\psi}$

Auf den Hintergrund der Vereinfachung des Schwerpunktsatzes wird im Rahmen der entsprechenden Komponente näher eingegangen.

Durch Integration von $_K\dot{\beta}$ ergibt sich der Schwimmwinkel des Fahrzeugs $_K\beta$ . Der Schwimmwinkel der Vorder- und Hinterachse $\beta_v$ und $\beta_h$ kann jeweils aus dem Schwimmwinkel des Fahrzeugs $_K\beta$ , dem Schwerpunktabstand zur Vorder- bzw. Hinterachse $l_v$ bzw. $l_h$ , der Gierwinkelgeschwindigkeit $_K\dot{\psi}$ und der Fahrzeuglängsgeschwindigkeit $_Kv_{Cx}$ berechnet werden.

$\beta_v = \beta + \frac{l_v \cdot _K\dot{\psi}}{_Kv_{Cx}}$

$\beta_h = \beta - \frac{l_h \cdot _K\dot{\psi}}{_Kv_{Cx}}$

Räder

Der Achs-Schräglaufwinkel ist der Winkel zwischen der Reifenlängsachse und dem Geschwindigkeitsvektor des Radmittelpunkts. Daher ergeben sich die Achs-Schräglaufwinkel der Vorder- und Hinterachse $\alpha_v$ und $\alpha_h$ aus der Differenz des jeweiligen Lenk- und Schwimmwinkels.

$\alpha_v = \delta_v - \beta_v$

$\alpha_h = \delta_h - \beta_h$

Basierend auf den Achs-Schräglaufwinkeln lassen sich zusammen mit der jeweiligen Achssteifigkeit $c_v$ und $c_h$ die Querkräfte an den Rädern bzw. Achsen berechnen.

$_RF_{yv} = c_v \cdot \alpha_v$

$_RF_{yh} = c_h \cdot \alpha_h$

Karosserie

Nach dem Skript^[2] wird beim linearen Einspurmodell von kleinen Winkeln ausgegangen und damit ergeben sich damit folgende Formeln für die Kräfte in x- und y-Richtung.

$_KF_{xv} \approx \delta_v \cdot _RF_{yv}$

$_KF_{xh} \approx \delta_h \cdot _RF_{yh}$

$_KF_{yv} \approx _RF_{yv}$

$_KF_{yh} \approx _RF_{yh}$

Aus den Kräften in x- und y-Richtung werden jeweils die Kräftesummen $_KF_{Cx}$ und $_KF_{Cy}$ gebildet. Durch einsetzen können die folgenden Formeln gebildet werden.

$_KF_{Cx} = \delta_v \cdot _RF_{yv} + \delta_h \cdot _RF_{yh}$

$_KF_{Cy} = _RF_{yv} + _RF_{yh}$

Durch das Dividieren der jeweiligen Kräfte (in x- und y-Richtung) mit der Masse des Fahrzeugs ergeben sich die Fahrzeuglängsbeschleunigungen in x- und y-Richtung.

$_Ka_{Cy} = \frac{_KF_{Cy}}{m}$

$_Ka_{Cx} = \frac{_KF_{Cx}}{m}$

Der Schwerpunkt Abstand der Hinterachse $l_h$ ergibt sich aus der Differenz von dem Radstand $l$ minus dem Schwerpunkt Abstand zur Vorderachse $l_v$ .

$l_h = l - l_v$

Mithilfe des Drallsatzes lässt sich die Gierwinkelbeschleunigung $_K\ddot{\psi}$ berechnen. Dabei wird die Differenz der Produkte aus dem Schwerpunktabstand zur Vorder- bzw. Hinterachse $l_v$ bzw. $l_h$ und den jeweiligen Querkräften durch die Massenträgheit $J_{zz}$ geteilt.

$_K\ddot{\psi} = \frac{l_v \cdot _KF_{yv} - l_h \cdot _KF_{yh}}{J_{zz}}$

Gierwinkel

Durch Integration der Gierwinkelbeschleunigung $_K\ddot{\psi}$ ergibt sich die Gierwinkelgeschwindigkeit $_K\dot{\psi}$ .

Programmierung

Die Programmierung beinhaltetet zwei unterschiedliche Komponenten. Die Simulation erfolgt über das Simulink Modell und die Parameter werden vom Parameterskript aus MATLAB übergeben.

Parameterskript

Das Parameterskript übergibt zunächst alle im Modell benötigten Parameter:

Im Anschluss werden die möglichen Fahrmannöver definiert. Es werden zudem Benutzerabfragen eingebaut, welche die Interaktion mit dem Skript bestimmen. Die Eingaben vom Benutzer werden nur dann übernommen wenn es sich um Eingaben innherb des Definitionsbereiches handelt. Zum Beispiel werden 4 Fahrmannöver definiert, welche die Nummer 1-4 Zugewiesen wird. Im Anschluss kann der Benutzer eine freie Eingabe tätigen, wenn nun eine 5 oder eine andere Zahl/Buchstabe außerhalb des Definitionsraumes eingeben wird bekommt der Nutzer eine Fehlermeldung und die Ausführung des Skriptes wird abgebrochen. Die gleiche Vorgehensweise wurde für die Auswahl einer Links- oder Rechtskurve implementiert. Außerdem wird eine dritte Eingabe vom Benutzer gefordert, welche Abfragt ob er eine Darstellung des Simulationsergebnisses wünscht oder nicht. Der gesamte MATLAB-Code des Parameter Modells kann im SVN eingesehen und ausprobiert werden.

Ergebnisse

Zusammenfassung

Dokumentation

Link zu der Ausarbeitung in SVN

→ zurück zum Hauptartikel: "Systems Design Engineering" - Seminaraufgabe SoSe 2021: Einspurmodell“

↑ Göbel, M.: Fahrwerkmanagement Skript, Ostfalia Hochschule für angewandte Wissenschaften, Version 1.7, 10.06.2020
↑ Göbel, M.: Fahrwerkmanagement Skript, Ostfalia Hochschule für angewandte Wissenschaften, Version 1.7, 10.06.2020

[1] Göbel, M.: Fahrwerkmanagement Skript, Ostfalia Hochschule für angewandte Wissenschaften, Version 1.7, 10.06.2020

[2] Göbel, M.: Fahrwerkmanagement Skript, Ostfalia Hochschule für angewandte Wissenschaften, Version 1.7, 10.06.2020

[1]

[2]

@@ Zeile 108: / Zeile 108: @@
 | <math> _Kv_{Cx} </math>
 | Fahrzeuglängsgeschwindigkeit im Fahrzeugschwerpunkt C
-| <math> \fraq{m}{s} </math>
+| <math> \frac{m}{s} </math>
 |-
 | <math> _Ka_{Cy} </math>
 | Fahrzeugquerbeschleunigung im Fahrzeugschwerpunkt C
-| <math> \fraq{m}{s^2} </math>
+| <math> \frac{m}{s^2} </math>
 |-
 | <math> _Ka_{Cx} </math>
 | Fahrzeufglängsbeschleunigung im Fahrzeugschwerpunkt C
-| <math> \fraq{m}{s^2} </math>
+| <math> \frac{m}{s^2} </math>
 |-
 | <math> _KF_{Cy} </math>