Objekterkennung mit RP Lidar A1M8

Autor: Thomas Miska
Betreuer: Prof. Schneider

Slamtec: RPLiDAR A1

Aufgabenstellung

1. Einarbeitung in die bestehende Software
2. Softwareentwurf in MATLAB
   1. Meilenstein 1:
      1. Ansteuerung des RP LiDAR A1M8
      2. Koordinatentransformation polar- zu karthesisch
      3. Testdokumentation der KOS-Trafo
      4. Objektbildung (z.B. Sukzessiv Edge Following)
      5. Testdokumentation der Objektbildung
   2. Meilenstein 2:
      1. Objekttracking (mit Kalman-Filter)
      2. Testdokumentation des Objekttrackings
      3. Attribute schätzen: v, a, B, T, Güte (s. Schnittstellendokument)
      4. Testdokumentation der Attribute mit Referenz
      5. Dokumentation im Wiki
3. Softwareentwurf in C
   1. Meilenstein 3:
      1. Test der Kommunikation Kamera/LiDAR mit DS1104
      2. Testdokumentation
      3. Diagnoseseite in ControlDesk
      4. Darstellung der LiDAR-Objekte als XY-Plot und tabellarisch
      5. ggf. Fertigstellung der Kommunikation
   2. Meilenstein 4:
      1. Plausibilisierung der Messdaten (LiDAR, Kamera)
      2. Referenzmessungen
      3. Abschätzung der Güte der Spurerkennung und des Objekttrackings
      4. Dokumentation im Wiki

Softwareentwurf in MATLAB

Ansteuerung des RP LiDAR A1M8

Die Ansteuerung des RPLiDAR mit MATLAB Erfolgt in Verbindung mit einer SDK welche in C-Code geschrieben ist. Dieser Code ist in GitHub frei zugänglich. Der RPLiDAR liefert uns in diesem Fall folgende Messwerte:

• Radius
• Radiant
• Qualität

Die beiden folgenden Messdaten konnten nicht spezifiziert werden und wurden im weiteren Verlauf auch nicht verwendet. Sie befinden sich jedoch im Algorithmus, da der C-Code diese zurückgibt und diese schlussendlich definiert werden müssen.

• bNewScan
• Result

Die Verbindungsart beruht auf eine UART - Schnittstelle, die mithilfe eines Chips ermöglicht wird. Um den COM-Port zu definieren wird ein Textdokument zu Hilfe genommen, in es weitere Einstellungsmöglichkeiten gibt. Die Verwendung eines Textdokument liegt an daran, dass der C-Code ebenfalls darauf zugreift.

Quellcode in MATLAB

% Lade Bibliothek
hardwarex_init;

% Stelle Verbindung mit RPLiDAR her
pRPLIDAR = CreateRPLIDAR();
[result] = ConnectRPLIDAR(pRPLIDAR, 'RPLIDAR0.txt') % Lade die Konfigurationsdatei
disp('Neue Verbindung hergestellt')

[...]

Der Aufruf einer Messung erfolgt über folgenden Befehl:

[result, distance, angle, bNewScan, quality] = GetScanDataResponseRPLIDAR(pRPLIDAR);

Nach folglich ist der Code für das schließen der Verbindung:

Der Aufruf einer Messung erfolgt über folgenden Befehl:

[...]
% Schließe die RPLiDAR Verbindung
[result] = DisconnectRPLIDAR(pRPLIDAR)
DestroyRPLIDAR(pRPLIDAR);
clear pRPLIDAR; % unloadlibrary might fail if all the variables that use types from the library are not removed...
unloadlibrary('hardwarex');
disp('Verbindung wurde aufgehoben')

Koordinatentransformation polar- zu kartesisch

Abb. 1: Polar- und Kartesische Koordinaten

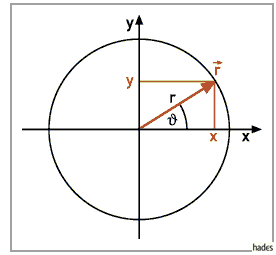
Um die Messwerte darstellen zu können bedarf es einer Umrechnung von Polarkoordinaten (Radius und Radiant) in kartesische Koordinaten (x und y Koordinaten). Das rechte Bild (Abb.1) stellt den Zusammenhang zwischen diesen beiden Formen dar. Folglich wird folgende Formel im MATLAB Code verwendet:

$x = radius * cos(\vartheta )$

$y = radius * sin(\vartheta )$

Folgender Code berechnet die kartesichen Koordinaten in MATLAB:

x = alldistances.*cos(allangles); % Koordinatentransformation in X-Achse
y = alldistances.*sin(allangles); % Koordinatentransformation in Y-Achse

LiDARfests KOS zu Fahrzeugfestes KOS

Für den weiteren Verlauf wird das Koordinatensystem auf das Fahrzeug übertragen. Hierzu werden folgende Werte:

• Index: L (LiDARfest)
• Einheit/Skalierung: m
• Ursprung: Mitte
• x-Achse: nach links/rechts
• y-Achse: nach oben/unten
• z-Achse: keine vorhanden

auf das folgende Koordinatensystem transformiert:

Fahrzeugfestes KOS

• Index: K (körperfest, karosseriefest)
• Einheit/Skalierung: mm
• Ursprung: Mitte Vorderkante des vorderen Stoßfängers des Fahrzeugs (z = 0)
• x-Achse: nach vorne (im Sinne der Hauptfahrtrichtung)
• y-Achse: nach links
• z-Achse: nach oben

Hierzu wird eine Distanzmatrix erstellt, die für die Transformation verwendet werdet. Diese Distanzmatrix bezieht sich auf das Fahrzeug, mit der Fahrzeugabmessungen auf die Werte subtrahiert werden. Mit diesem Schritt werden die Abstände von Objekten auf das Fahrzeug übertragen, sodass z.B. beim einparken nicht vom LiDAR aus gemessen wird. Nachfolgend der Code für die Distanzmatrix und die Transformation:

% Distanzmatrix
distanceX = -0.008; % in m (80mm)
distanceY = -0.0145; % in m (145mm)

[...]

% Transformation von LiDARfesten ins Körperfeste KOS
x=[Segment(cnt).LeftCartesian(1)-distanceX  Segment(cnt).NearbyCartesian(1)-distanceX Segment(cnt).RightCartesian(1)-distanceX];
y=[Segment(cnt).LeftCartesian(2)-distanceY  Segment(cnt).NearbyCartesian(2)-distanceY Segment(cnt).RightCartesian(2)-distanceY];

Objektbildung

Abb. 2: Beispiel der Koordinatentransformation mit Objektbildung, Segmente in rot, Messwerte in blau

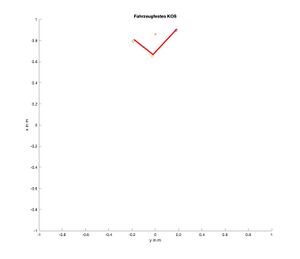
Es gibt mehrere Varianten eine Objektbildung durchzuführen. Für das Projekt jedoch wurde ein Successive Edge Following (SEF) Algorithmus verwendet. Dieser Code vergleich dabei nebeneinanderliegende (unter Zuhilfenahme des Winkels vom RPLiDAR) die Radius-Messwerte miteinander und falls diese eine kleine Differenz zueinander aufweisen wird ein Segment gebildet.

Links im Bild (Abb. 2) ist ein Beispiel für die Objektbildung dargestellt. Die roten Linien Kennzeichen das Objekt. Die Ecken und die vordere Mitte wurden markiert.

Aus diesen Segmenten lassen sich Objekteigenschaften bilden. Die Objekte werden mit einer Breite, Tiefe und Objektausrichtung bestimmt.

Nachfolgend der Code für das bestimmen der Objekteigenschaften:

% Breite und Tiefe und X und Y Koordinate des Objektmittelpunktes
 a = sqrt((x(1)-x(2))^2+(y(1)-y(2))^2);
 b = sqrt((x(2)-x(3))^2+(y(2)-y(3))^2);
 c=  sqrt((x(1)-x(3))^2+(y(1)-y(3))^2);
 centerX = (x(1)+x(3))/2;
 centerY = (y(1)+y(3))/2;

   if(a>b)
           objWidth = b; objDepth=a;
         center_vorneX = (x(3)+x(2))/2;
         center_vorneY = (y(3)+y(2))/2; 
   else
           objWidth = a; objDepth=b;
         center_vorneX = (x(1)+x(2))/2;
         center_vorneY = (y(1)+y(2))/2;
   end

    K= (centerY-center_vorneY)/(centerX-center_vorneX);
    objAngle = rad2deg(atan((K)));
      if K>0
          if(centerY<center_vorneY)
            objAngle=objAngle-90;
          else
          objAngle=90-objAngle;
          end
      else
           if(centerY<center_vorneY)
            objAngle=objAngle+180;
           else    
          objAngle=-(objAngle+90);
           end
      end

  if (K == inf ||K == -inf || K ==0 || y(2)-y(1))/(x(2)-x(1)) == (y(1)-y(3))/(x(1)-x(3))
      objWidth= c; objDepth=0;
      center_vorneX = (x(1)+x(3))/2;
      center_vorneY = (y(1)+y(3))/2;
      objAngle=0;
 end

Objekttracking (mit Kalman-Filter)

Abb. 2: Beispiel für das Resultat des Kalmanfilters

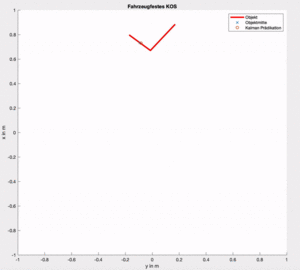
Da die Messwerte eine Ungenauigkeit aufweisen, muss ein Kalmanfilter verwendet werden um die statischen Elemente auf der Strecke, als statisch zu erkennen. Aktuell springen die Objekte in einem kleinen Bereich. Der Kalmanfilter korrigiert diesen Anteil. Ebenfalls kann mit dem Kalmanfilter die Geschwindigkeit und die Beschleunigung des Objektes geschätzt werden.

Nachfolgend der angepasste Code von Phil Kim.

% Beim ersten Durchlauf Variblen initialisieren
if isempty(firstRun)
  % Abtastzeit
  dt = 0.2;
  
  % Systemmatrix der linearen Zustandsraumdarstellung
  A = [ 1   0   dt  0       (dt^2/2)  0
        0   1   0   dt^2    0         (dt^2/2)
        0   0   1   0       dt        0
        0   0   0   1       0         dt
        0   0   0   0       1         0
        0   0   0   0       0         1];
  
  %Beobachtungsmatrix der linearen Zustandsraumdarstellung
  H = [ 1  0  0  0  0  0
        0  1  0  0  0  0];
 
  % Kovarianzmatrix des Systemrauschens
  Q = 0.000001*[ 1        0        dt       0        (dt^2/2)  0
            0        1        0        dt       0         dt^2
            dt       0        dt^2     0        (dt^3/2)  0
            0        dt       0        dt^2     0         (dt^3/2)
            (dt^2/2) 0        (dt^3/2) 0        (dt^4/4)  0 
            0        (dt^2/2) 0        (dt^3/2) 0         (dt^4/4)];
  % Kovarianzmatrix des Messrauschens
  R = [ 0.0240^2  0
        0     0.0283^2 ];

  % Systemzustandsvektor eines linearen dynamischen Systems   
  x = [0, 0, 0, 0, 0, 0]';
  % Kovarianzmatrix des Schätzfehlers
  P = 100*eye(6);
  
  firstRun = 1;
end

%% Kalman Gleichungen

% Prädikationsprozess
xp = A*x;               % Prädikation der Schätzung
Pp = A*P*A' + Q;        % Prädikation der Fehlerkovarianz

% Schätzprozess
K = Pp*H'*inv(H*Pp*H'+R);% Kalman-Verstärkung K
z = [xm ym]';           % Messwerte
x = xp + K*(z - H*xp);  % Zustandsschätzung
P = Pp - K*H*Pp;        % Kovarianzschätzung

%% Rückgabewerte
xh = x(1); % x-Position 
yh = x(2); % y-Position
% Geschwindigkeit
vx = x(3);
vy = x(4);
% Beschleunigung
ax = x(5);
ay = x(6);

Getting started

• MATLAB Beispiel
• GitHub Beispiel
• Datenblatt
• Code in SVN

---

→ zurück zum Hauptartikel: SDE Praktikum Autonomes Fahren