Drucksensor mit Matlab/Simulink

Sensor: dPressure 500

Autor: Ilja Scheremeta Betreuer: Prof. Schneider

Aufgabenstellung

In dem Fach "Signalverarbeitende Systeme" aus dem Studiengang "Business and Systemsengineering" der Hochschule Hamm-Lippstadt obliegt jedem Studierenden die Aufgabe sich semesterbegleitend mit einem ausgewählten Sensor auseinander zu setzen. In diesem Zusammenhang soll der jeweilige Sensor im Laufe der Ausarbeitung mit MATLAB/Simulink ausgelesen und im Anschluss im HSHL Wiki sinnvoll und verständlich dokumentiert werden.

Der Sensor und seine Funktionsweise

Bei dem dPressure 500 Sensor für Lego Mindstorms NXT handelt es sich um einen analogen Silizium-Drucksensor, mit dem verschiedene Druckschwankungen gemessen werden können. Dieser Sensor arbeitet mit einem Mikroprozessor, welcher die A/D-Wandlung unterstützt und er weist folgende technische Daten auf:

Abb. 1: dPressure 500

Merkmal	Werte
Messbereich	von 0kPa (Vakuum) bis 500kPa (70psi)
Messbereich (Rohsignal)	von 0V bis 5V
Messbare Schwankungen	0,25kPa (0,05psi)
Genauigkeit	+/- 2,5%
Mittlere Antwortzeit	1ms
Betriebsversorgungsspannung	4,75V bis 5,25V
Betriebsversorgungsstrom	7mA
Betriebstemperatur	0°C bis 85°C

Abb. 2: Die Funktionsweise des Sensors

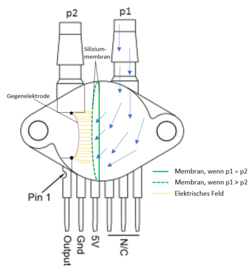
In der Messtechnik gibt es je nach Messverfahren unterschiedliche Drucksensoren. Der dPressure500 gehört zu dem Typen des kapazitiven Differenzdrucksensors. Es bedeutet, dass hierbei die Differenz zweier Absolutdrücke p1 und p2 gemessen und miteinander verglichen wird. Aus diesem Grund besitzt der Sensor zwei separate Druckanschlüsse und arbeitet im Vergleich zu vielen anderen Drucksensoren ausschließlich in einem positiven Bereich, wobei p1 den Druck darstellt, der im Vergleich zu p2 verändert wird und p2 immer konstant bleibt (p1≥p2). In diesem Fall liegt der Messbereich zwischen 0kPa und 500kPa.

Außerdem besitzt dPressure500 demzufolge zwei Messkammer, die durch eine Siliziummembran hermetisch voneinander getrennt sind. Die Funktionsweise hierbei ist wie bei einem Plattenkondensator mit einem variablen Elektrodenabstand. Die Siliziummembran und die Gegenelektrode stellen an dieser Stelle die beiden Elektroden des Kondensators dar und die Luft dazwischen ist das Dielektrikum. Erhöht sich der Druck p1, so biegt sich die Membran durch und der Abstand zwischen den Elektroden und dadurch die Kapazität des Kondensators wird verringert. Durch die Veränderung des Abstandes wird auch der Stromfluss und somit die Ausgangsspannung Vout als das Rohsignal beeinflusst. Dessen Messbereich liegt zwischen 0V und 5V. Die Biegung der Membran bzw. der Abstand zwischen dem Siliziummembran und der Gegenelektrode ist also in diesem Zusammenhang ein Maß für die Größe des Differenzdruckes (s. Abb. 2).

Vorverarbeitung

[[Datei:Kennlinie_des_Sensors.PNG|thumb|300px|right|Abb. 3: Kennlinie des Sensors]] Aus der Funktionsweise des Sensors dPressure500 kann entnommen werden, dass die Messwerte in Form von Spannung Vout in der Signalverarbeitungskette direkt an Arduino übertragen werden. Diese Werte müssen dann durch eine Funktion in die Druckeinheit Pascal umgewandelt werden. Das Verhältnis zwischen der Ausgangsspannung Vout und dem Druck kPa wird anhand von einer Kennlinie wie folgt dargestellt (s. Abb. 3).

Analog-Digital-Umsetzer

Abb. 4: 10-Bit SAR-Wandler

Der Drucksensor dPressure 500 wird zur Signalverarbeitung mit einem der sechs analogen Pins des Arduino Uno (A0-A5) verbunden. Damit werden die analogen Signale in Form von Spannung gemessen und danach digitalisiert. Grundsätzlich haben die analogen Signale im Vergleich zu digitalen Signalen einen Vorteil, indem sie sehr viele Werte zwischen einem hohen und niedrigen Pegel annehmen können. Beim Arduino UNO liegt der maximale Pegel bei 5 V und der niedrigste bei 0V. Außerdem arbeitet der Arduino mit dem ATMEGA328P-MU Mikrocontroller, bei dem die Auflösung des ADCs 10-Bit (1024 Messwerte) beträgt. Das Auslesen einer Messung am Eingang dauert ca. 0,0001 Sekunden, so dass maximal 10.000 Messungen pro Sekunde verarbeitet werden können. Die eben erwähnten Werte zwischen 0 V und 5 V werden von dem integrierten 10-Bit Analog Digital Wandler (ADC) in Integer Werte zwischen 0 bis 1023 umgewandelt. Ein Signal kann hierbei eine Auflösung von 4,9mV aufnehmen:

$\frac{5 V}{1023} = 4,88 mV.$

Der Analog Digital Wandler arbeitet bei dem eingebauten Microcontroller mit der sukzessiven Approximation. Dabei spricht man um eine schrittweise Annährung des eingehenden Signals mittels der Ausgangsspannung eines DA-Wandlers. Hierbei wird also die analoge Eingangsspannung (unendlicher Wertebereich) so lange mit der Referenzspannung verglichen bis das richtige Ergebnis identifiziert und digital (endlicher Wertebereich) dargestellt wird. Solch ein ADU besteht aus einem DA-Wandler, SAR-Datenregister, einer elektronischen Schaltung für die digitale Steuerelektronik und einem separaten Komparator. SAR steht für Seccessive Approximation Register und darin wird am Ende des Vorgangs der ermittelte Digitalwert des DA-Wandlers dargestellt. Der Komparator dagegen vergleicht dabei die erzeugte Referenzspannung vom DA-Wandler mit der Eingangsspannung.

Beispiel für die sukzessive Approximation

Abb. 5: 3-Bit SAR-Wandler

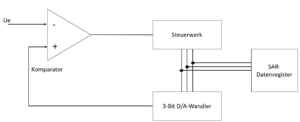
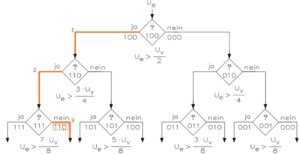
Im folgenden Beispiel wird die „sukzessive Approximation“ anhand von einem verhältnismäßig übersichtlichen 3-Bit-Wandler genauer erklärt (s. Abb. 5 u. 6). Da es sich um einen 3-Bit-Wandler handelt, können an dieser Stelle 8 Messwerte dargestellt werden. Es wird angenommen, dass sich der Pegel der Messwerte der zu vermessenden Eingangsspannung zwischen 0 V und 7 V befindet und die digitale Darstellung der Messwerte ausschließlich in ganzen Zahlen erfolgt. So ergibt sich hierfür die folgende Binärtabelle:

Abb. 6: 3-Bit Flussdiagramm mit Eingangsspannung von 6 V

Binärdarstellung	Spannung in V
000	0
001	1
010	2
011	3
100	4
101	5
110	6
111	7

Abbildung 5 veranschaulicht über ein Flussdiagramm die erwähnte schrittweise Annährung des eingehenden Signals in Form von Ue. Dabei finden insgesamt drei Vergleiche statt. Die zu vermessene Spannung wird als erstes mit dem MSB (Most Significant Bit) auf den Binärwert 100 gesetzt. Darauf hin wird im DA-Wandler die entsprechende Ausgangsspannung erzeugt, die mit der eigentlichen Messspannung im Komparator verglichen wird. Hier bekommt man einen Vergleich, ob die Messspannung größer oder kleiner als die Vergleichsspannung (Uv) ist. Da es im gegebenen Fall größer ist, wird das MSB in der SAR-Einheit gesetzt und es kommt zum nächsten Schritt und somit zum nächsten Vergleich. In diesem und im letzten Schritt wiederholt sich dieser Vorgang bis am Ende eine Binärzahl 110 übrigbleibt. Diese steht für 6 V und wird abschließend in dem SAR-Datenregister dargestellt.

Abb. 7: Der Schaltkreis des Sensors

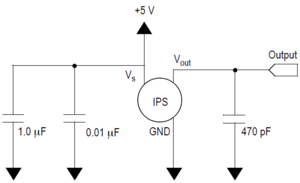
LC-Filter Wie man aus der Abbildung 7 entnehmen kann, besteht der Schaltkreis des Sensors laut dem Datenblatt aus Kondensatoren und Spulen. Dies ist ein Merkmal dafür, dass ein LC-Filter verwendet wurde. Durch solch einen Filter kann eine Verbesserung der Flankensteilheit erreicht werden. Die Flankensteilheit beschreibt hierbei, wie stark der Filter beim erreichen der Grenzfrequenz reagiert. Dabei gilt es, je höher die Flankensteilheit, desto höher die Filterwirkung. Die LC-Bandpässe werden grundsätzlich durch den Einsatz von zwei magnetisch gekoppelten Parallelschwingkreisen umgesetzt. Diese sind in dem Schaltkreis in Form von IPS (Inductive Power Supply = Drahtlose Energieübertragung) dargestellt.

Bussystem

In diesem Projekt wird der Sensor dPressure 500 direkt über einen Arduino Uno Board verbunden. Dieser kommuniziert über drei der auf dem Arduino Uno eingebauten GPIO Pins. Die GPIOs sind allgemein beschrieben die Lötpunkte in Form einer Stiftleiste und sind die Schnittstellen zu anderen Systemen oder Schaltungen. Außerdem ist das Verhalten dieser GPIOs unabhängig von den Eingabe- oder Ausgabekontakten und sind durch logische Programmierung frei bestimmbar. An dieser Stelle lässt sich sagen, dass ein konkretes Bussystem nicht erkennbar ist.

Digitale Signalverarbeitung

Vor der Erläuterung der gesamten Signalverarbeitung vom Sensor bis hin zum MATLAB, muss zunächst geklärt werden welche Hardware und Software für dieses Projekt benutzt wurden:

Hardware

• Laptop

• Arduino UNO

• dPressure 500

• NXT EV3 Kabel

• Wire Jumper

• USB A/B Kabel

Software

• Microsoft Windows 10

• Matlab R2017a

• Fritzing

Für den dPressure 500 wurde der Ansatz verfolgt, die Kommunikation zwischen dem Sensor und MATLAB mithilfe von Arduino Uno zu gewährleisten. Der Sensor besitzt einen EV3 Anschluss. Dies ist insofern praktisch, da es direkt mit dem Arduino Uno über die GPIO Pins verbunden werden kann. Da das EV3 Kabel einen inkompatiblen Anschluss für den Arduino UNO besitzt, wurde ein Ende des EV3 Kabels abgeschnitten und nur die benötigten Anschlüsse mit zusätzlichen Jumpern zusammengelötet. Damit wurde ermöglicht, dass der Sensor direkt über die GPIO Pins an Arduino angeschlossen werden konnte. Laut dem Datenblatt des Sensors werden für die digitale Signalverarbeitung nur drei von den sechs vorhandenen Pins benötigt (s. Abb. 2). Diese werden mit den GPIO Pins des Arduinos wie folgt verbunden:

Abb. 8: Der Schaltplan

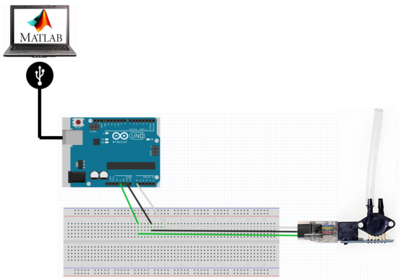
Pin	Funktion	Farbe des Jumpers
1	Vout	weiß
2	Ground	schwarz
3	Vcc	grün
4	keine
5	keine
6	keine

Am Arduino befindet sich außerdem eine USB Typ-B Buchse. Darüber wird direkt über einen USB A/B Kabel der Arduino mit dem Laptop verbunden.

MATLAB Simulation

Nun wird mithilfe von MATLAB eine Verbindung zum Sensor hergestellt. Hierzu wird zunächst das Package „MATLAB Support Package for Arduino Hardware“ benötigt. So bald es installiert ist, wird die Kommunikation zwischen MATLAB und dem Sensor hergestellt. Dieser Schritt erfolgt zum größten Teil automatisch und wird lediglich durch den Befehlt a = arduino im Editor unterstützt. Im zweiten Schritt wird ein Code geschrieben mit dem auf einzelne Messwerte in der Einheit Druck (kPa) und (PSI) zugegriffen werden kann. Abschließend wird ein Code generiert, mit dem eine live Datenübertragung der Messwerte stattfindet. Der Code zu den eben erwähnten Schritten sieht wie folgt aus:

            %% mit Arduino verbinden

a = arduino;                                                %Verbindung des Arduinos mit MATLAB

            %% Einzelmessung von kPa und PSI

v = readVoltage(a,'A0')                                     %%in Volt
n = (0: 0.0049: 500);                                       %%kPa

kPa = (v - 0.2)/0.009;                                      %%Volt in kPa umrechnen
PSI= kPa*(0.145037738);                                     %%Volt in PSI umrechnen
fprintf('Einzelmessung:\n  %.1f kPa\n  %.1f PSI\n',kPa,PSI)

            %% Messwerte live auslesen
Messzeit = 500;                                             %%Intervall der Messzeit in ds
init_time =1;                                               %%Startzeit
x = 0;                                                      %%Start Druck

while (init_time < Messzeit)                                %%Funktion plotten
    b=((readVoltage(a, 'A0'))-0.2)/0.009;
    x=[x,b];
    plot(x);
    grid on
    init_time=init_time+1;
    xlabel('Zeit in Dezisekunden');
    drawnow
end

Testmessung

Abb. 10: Die manuelle Messmethode

Um zu überprüfen, ob der Sensor überhaupt misst und die digitale Signalverarbeitung vom Sensor bis hin zu der Ausgabe im MATLAB richtig funktionieren, wurde zunächst eine Testmessung durchgeführt. Hierzu wurde eine manuelle Messmethode angewendet. Hierbei wurde der Schlaucht an dem Sensor, der sich an dem Druckanschluss p1 (s. Abb. 8) befindet, mit einer 12ml Spritze befestigt. Über diese Spritze kann auf die angeschlossene Kammer bestimmter Druck ausgeübt werden. Dieser hängt von der ausgeübten Kraft F und der gedrückten Fläche A ab.

$\frac{F}{A} = p.$

Bei dieser Messung wurde als erstes der Kolben der Spritze am Anschlag positioniert. Daraufhin wurde der Sensor mit der Spritze über den Schlauch verbunden. Nach dem Start der Software, wurde in dem eingegebenen Zeitintervall von 500ds der Kolben nach unten gedrückt und kurz darauf bis auf 10ml losgelassen. Dieser Vorgang wurde so lange durchgeführt bis die eingestellte Zeit abgelaufen ist. Die Ergebnisse zu dieser Messung sind in der Abbildung 9 zu sehen. Der Link zu dem Video dieser Messung ist unter der Überschrift „Video“ verlinkt.

Abb. 9: Ergebnisse der Testmessung

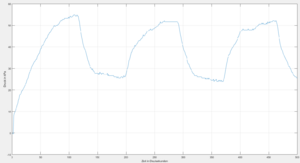
Darstellung der Ergebnisse

Abb. 11: PAP zu einer Versuchsreihe

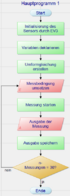
Zur Bestimmung der Messunsicherheit und des Vertrauensintervalls, wurde mit der eben erwähnten Methodik gemessen. Dennoch handelt es sich hierbei nicht um eine Echtzeitmessung, sondern um vielen Einzelmessungen. Insgesamt wurden 30 Messungen je fünf Versuchsreihen durchgeführt. Die Vorgehensweise jeder einzelnen Versuchsreihe ist in der Abbildung 11 dargestellt und der dazu gehörige Baustein der „Messbedingung umsetzen“ besteht aus den folgenden sechs Schritten:

Vorgehensweise bei "Messbedingung umsetzen"

1. Den Kolben bis zum Anschlag bringen

2. Den Schlauch des Sensors und die Spritze verbinden

3. Den Kolben auf festgelegte Marke drücken

4. Ergebnis notieren

5. Den Schlauch und die Spritze trennen

6. Den Kolben bis zum Anschlag bringen

Die Messbedingungen, so wie die Messergebnisse sind aus der folgenden Tabelle zu entnehmen:

Messergebnisse

Messreihe	Bedingung	Anzahl Messungen	Referenzwert in kPa	Druck in kPa min	Druck in kPa max	Mittelwert in kPa	Standartabweichung	Messunsicherheit	Vertrauensbereich
1	Anschlag bis 12ml	30	6,61	6,51	7,06	6,87	0,275	0,55	6,87 ± 0,55
2	Anschlag bis 11ml	30	15,12	15,2	16,3	15,47	0,428	1,1	15,47 ± 1,1
3	Anschlag bis 10ml	30	24,9	25,52	26,6	25,85	0,424	1,08	25,85 ± 1,08
4	Anschlag bis 9ml	30	36,77	36,93	38,01	37,63	0,44	1,1	37,63 ± 1,1
5	Anschlag bis 8ml	30	51,2	51,59	52,67	52,02	0,346	1,08	52,02 ± 1,08

Auf der Suche nach den negativen Einflüssen auf die Messergebnisse wurde bei diesem Projekt das Ishikawa-Diagramm betrachtet. Darüber hinaus wurden folgende Einflüsse identifiziert:

Negative Einflüsse auf die Messergebnisse

1. Messobjekt

Als Messobjekt dient eine Spritze. Diese hat eine analoge Skala, die die restliche Luft in der Spritze in Form von ml hergibt. Aus diesem Grund ist es nicht möglich eine exakt gleiche Menge an Luft einzustellen, da das untere Ende des Kolbens größer als die analogen Markierungen sind. Man befindet sich somit fast immer minimal über oder unter der angenommenen Luftmenge.

2. Messgerät

Die Auflösung des Sensors beträgt 4,88mV. Dies bedeutet, dass etwa in Schritten von 0,5kPa das Ergebnis angezeigt werden kann. Für alle Werte dazwischen ist die Auflösung zu klein und wird somit ab- oder aufgerundet. Aus diesem Grund ist der Sensor für sehr kleine Druckwerte (0-10kPa) nicht geeignet.

3. Methode

Der Druck ist von dem Volumen, in dem der Druck gemessen werden soll, abhängig. Dies bedeutet, dass das Volumen von der Kammer des Sensors bis zum Anfang des Kolbens genau gleich sein muss, wie das gleiche Volumen des Referenzmessgerätes. Da dies aber nicht möglich ist zu berechnen, können hierbei geringe Einflüsse auf die Messergebnisse einwirken.