Temperatursensor mit Matlab/Simulink

Autor: Sergej Vogel
Betreuer: Prof. Schneider
Sensor: Lego Temperatursensor 9749

Aufgabenstellung

In dem Fach "Signalverarbeitende Systeme" aus dem Studiengang "Business and Systemsengineering" wurde jeder Student damit beauftragt, sich Semester begleitend mit einem Sensor auseinander zu setzen. Genauer gesagt, soll man sich über den Sensor informieren, sowie dessen Signale mittels MATLAB/Simulink verwertbar machen.

Primärsensor

Abb. 1: Temperatursensor

In diesem Kapitel soll der LEGO® MINDSTORMS® Temperatursensor (Artikel 9749) vorgestellt und erläutert werden (siehe Abb. 1). Leider gibt es sehr wenige Informationen zu dem Sensor. Aus diesem Grund habe ich den Kundenservice von Lego Mindstorms kontaktiert und um ein Datenblatt des Sensors gebeten. Nach Aussage des Kundenservice besitzen sie kein Datenblatt zu diesem Sensor. Dennoch war es möglich einige Daten zusammen zu bekommen.
Es handelt es sich um einen digitalen Sensor, der durch einen LEGO® MINDSTORMS® Education NXT (Software v.2.1) oder LEGO MINDSTORMS Education EV3 (EV3 Software) angesteuert und ausgelesen werden kann. Dabei findet die Kommunikation, zwischen dem Mikrocontroller und dem Sensor, über die I²C Schnittstelle statt. Dafür muss die 7 bit Adresse des Sensors angesprochen werden. Der Einsatz des Sensors liegt in dem Temperaturbereich: -20°C bis 120°C bzw. -4°F bis 248°F, wobei dieser erst kalibriert werden muss.
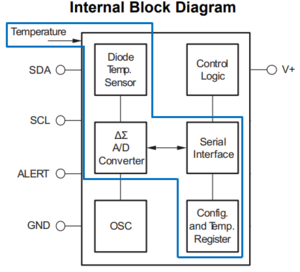
Laut Angaben, ist in dem NXT Gehäuse der Sensor von Typ TMP275 mit einem 12 Bit Analog-Digital-Umsetzer (ADU oder engl. Analog-Digital-Converter ADC oder A/D-Wandler) integriert. Die Temperaturaufnahme erfolgt hierbei mittels einer in dem TMP275 Sensor verbauten Diode und dem Fühlerrohr.

Signalverarbeitung

Das analoge Temperatursignal wird über das Fühlerrohr aufgenommen und an die, im Temperatursensor TMP275 integrierte, Temperaturdiode weitergeleitet. Die Diode erzeugt eine zur Temperatur proportionale elektrische Größe, die im weiteren Schritt an den 12-Bit A/D Wandler übergeben wird. Über die Diode ist nichts genaueres bekannt. Daraus resultiert ein 12-Bit Code, den es zu interpretieren gilt. Mit Hilfe der Tabelle aus dem Datenblatt des TMP275 Sensors, die sich unter dem Text befindet, wird eine Kennlinie erzeugt (siehe Abb.4), bei der jedem Signal eine bestimmte Temperatur zugeordnet wird.

Abb. 2: TMP275 Temperatursensor

Abb. 4: Kennlinie

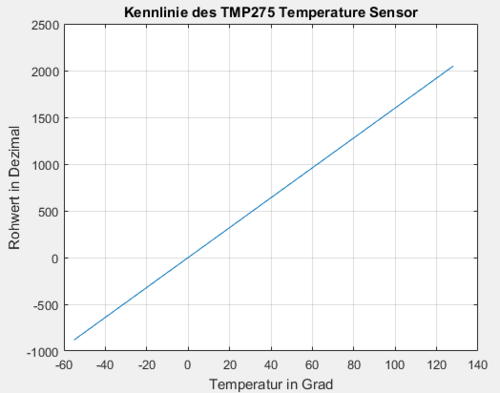
Temperatur in °C	Signale im Hexadezimalsystem	Signale im Dezimalsystem
128	7FF	2047
127.9375	7FF	2047
100	640	1600
80	500	1280
75	4B0	1200
50	320	800
25	190	400
0.25	004	4
0	0	0
-0.25	FFC	-4
-25	E70	-400
-55	C90	-880

Wird nun das jeweilige Signal des Sensors durch die dazugehörige Temperatur geteilt, so erhält man die Temperaturauflösung von 0,0625°C, was laut dem Datenblatt der typischen Auflösung entspricht. Durch die erhaltene Temperaturauflösung wird deutlich, dass 1°C in $1^\circ C/0,0625^\circ C=16$ Abstufungen dargestellt werden kann. In Kombination mit dem Messbereich des TMP275 welches bei -40°C bis 125°C liegt und in Summe einen Bereich von 165 Temperaturwerten abdeckt, lässt sich festhalten, dass man einen AD-Wandler benötigt, welcher $165\cdot16=2640$ Zustände darstellen kann. Somit ist es plausibel einen 12-Bit A/D Wandler zu nutzen, da dieser auf $2^{^12} = 4096$ Zustände kommt, während ein 11-Bit A/D Wandler nur $2^{^11} = 2048$ Zustände darstellen kann, was nicht ausreichend ist.

A/D-Umwandler:

Der A/D-Umwandler hat die Aufgabe, analoge (kontinuierliche) Werte aus dem unendlichen Wertebereich in einen endlichen (diskreten) Wertebereich abzubilden. Dies bedeutet, dass die kontinuierlichen Signale in bestimmten Zeitabständen abgetastet werden und in dem Augenblick, je nach Auflösung des ADUs, in einen wertediskreten Wert umwandelt. Somit kommt ein zeit- und wertediskretes Signal heraus. Um ein kontinuierliches Signal korrekt zu rekonstruieren, muss das Signal nach dem Shannonsche Abtasttheorem mit einer mindestens doppelt so hohen Frequenz abgetastet werden, als die Frenquenz des Signals ist. 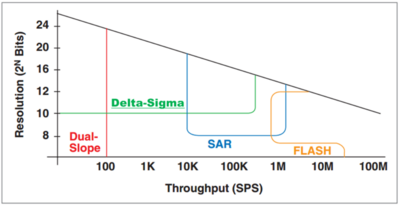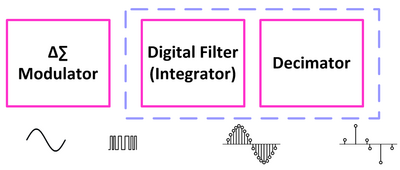Bei dem im TMP275 Sensor integrierten Analog-Digital-Wandler handelt es sich um den Delta-Sigma-Wandler (ΔΣ-ADC). Neben den anderen möglichen ADCs bietet der Sigma-Delta-Wandler eine gute Kombination aus hoher Auflösung und einem relativ hohen Durchsatz (siehe Abb.5). Dabei ist der Delta-Sigma-Modulator der Kern des ADC und ist verantwortlich für die Digitalisierung des analogen Eingangssignals bei gleichzeitiger Reduzierung des Rauschens durch Techniken wie Oversampling, Noise Shaping und Digitalfilter. Vereinfacht besteht der ΔΣ-ADC aus drei Hauptabschnitten (siehe Abb.6):

Delta-Sigma-Modulator:

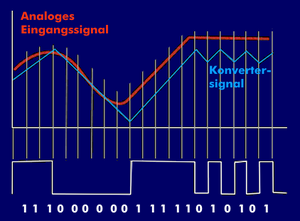
• Die Aufgabe des Modulators besteht darin, die analogen Eingänge in einen 1-Bit-modulierten digitalen Strom umzuwandeln. Genauer gesagt, arbeitet der Wandler nur mit einem Bit welches die Werte 0 und 1 annehmen kann. Bei dieser Art der A/D Wandlung werden lediglich die Pegelunterschiede von einem Abtastwert zum nächsten gekennzeichnet (siehe Abb.7).
  

Digital Filter (Integrator):

• Der Integrator integriert diesen einzelnen Bitstrom zu einem Mehrbitwert, der einen Durchschnittswert des Signals darstellt, jedoch mit vielen zusätzlichen Informationen.

Decimator:

• Schließlich entfernt der Decimator die zusätzlichen unnötigen Informationen, was zu einer Ausgabe führt, die genau ist, aber der korrekten minimalen Größe entspricht.

Bei der Umwandlung des analogen Signals in ein digitales, wird die Signalkurve in diskrete Werte unterteilt. Dies bedeutet, der Wandler entscheidet in den Situationen, in welchen diskreten Wert er das analoge Signal wandelt. Einfacher gesagt, das Signal wird je nach Auflösung auf- bzw. abgerundet. Dieser Unterschied zwischen dem analogen und konvertierten Signal wird als "Quantisierungsfehler" oder "digitales Rauschen" bezeichnet. Um das Rauschen zu reduzieren, werden die oben genannten Techniken kurz erläutert.

Oversampling:
Laut dem Abtasttheorem muss die Frequenz mit einer (mind.) doppelten Abtastrate abgetastet werden. Es gibt einige Möglichkeiten ein Signal abzutasten. Von Oversampling ist dann die Rede, wenn die Signale mit einer höheren Abtastrate abgetastet werden, als für die Darstellung der Bandbreite nötig wird. Dadurch wird das Quantisierungsrauschen minimiert, bleibt jedoch vorhanden.

Noise Shaping:
Das durch die Quantisierung entstandene Rauschen wird durch das Noise Shaping verringert. Dabei wird die Rauschenergie aus dem Audiobereich in einen höheren Frequenzbereich verschoben. Dadurch gehen diese Signale nicht in die Signalverarbeitung mit ein.

Abb. 5: Bits and Bandwidth

Abb. 6: DELTA-SIGMA BLOCK DIAGRAM

Abb. 7: 1-Bit-DeltaModulation

I²C Schnittstelle

Der I²C Bus (Inter Integrated Circuit) wurde von Philips konzipiert und stellt heute den Standard für die Systemsteuerung dar. Der Bus basiert auf einem Master-Slave-Prinzip und hat zwei Leitungen zur Verfügung. Die beiden Leitungen heißen Signal Data (SDA) und Signal Clock (SCL). Wie die Namen schon sagen, wird die SDA Leitung für Datenübertragung genutzt, während die SCL Leitung für den Takt zuständig ist. Der Takt wird durch den Master erzeugt, kann aber vom Slave solange auf 0 gehalten werden, bis der Slave wieder bereit ist. Die Daten können in beide Richtungen byteweise übermittelt werden. In diesem Fall stellt der Temperatursensor den Slave dar. Dieser hat eine eindeutige 7-Bit-Adresse, die der Master anspricht.

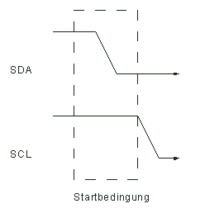
START-Bedingung

Zu Anfang befinden sich die beiden Leitungen im Leerlauf und werden durch Pullupwiderstände auf hohem Pegel gehalten. Zu diesem Zeitpunkt können keine Daten übertragen werden. Um eine Kommunikation zwischen Master und Slave herzustellen, muss eine Startbedingung erzeugt werden. Diese kommt Zustande, indem die SDA Leitung von HIGH auf LOW wechselt, während die SCL Leitung weiterhin auf HIGH bleibt. Erst dann beginnt die Datenübertragung. Hervorgerufen wird die Startbedingung durch den Master. Ab dem Moment befindet sich der Bus im Modus "beschäftigt".

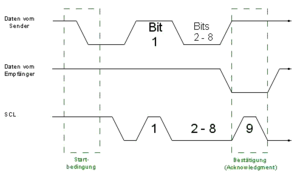
Adressierung und Read/Write (R/W)

Nach der Startbedingung beginnt die von dem Master ausgehende Kommunikation. Übertragen werden die Informationen byteweise (8-Bit). Damit sich ein Slave angesprochen fühlt, muss der Master die eindeutige Adresse des Slave ansprechen. Somit sendet der Master auf der SDA Leitung eine 7-Bit Adresse, um den Slave anzusprechen, gefolgt vom einem weiteren Bit mit der Information, ob der Master an den Slave eine Information senden (LOW), oder vom Slave Informationen erhalten möchte (HIGH). Dieses wird als Datenrichtungsbit bezeichnet.

Aknowledge (ACK) und Not Aknowledge (NACK)

Die Bestätigung ACK erfolgt nach jedem Byte. Dadurch teilt der Empfänger/Slave (in unserem Fall der Temperatursensor) dem Sender/Master mit, dass das Byte erfolgreich empfangen wurde und das nächste Byte gesendet werden kann. Damit es funktioniert, gibt der Master die SDA-Leitung während des Bestätigungstaktimpulses frei und der Slave zieht die SDA-Leitung auf LOW. Diese bleibt während der HIGH-Periode des Taktimpulses weiterhin auf LOW. Es gibt 5 Bedingungen die zu einem NACK führen:

1. Auf dem Bus ist kein Empfänger mit der übertragenen Adresse vorhanden, so dass kein Gerät mit einer Bestätigung antworten kann.
2. Der Empfänger kann nicht empfangen oder senden, da er eine Echtzeitfunktion ausführt und nicht bereit ist, die Kommunikation mit dem Master zu starten.
3. Während der Übertragung erhält der Empfänger Daten oder Befehle, die er nicht versteht.
4. Während der Übertragung kann der Empfänger keine weiteren Datenbytes mehr empfangen.
5. Ein Master-Empfänger muss das Ende der Übertragung an den Slave-Sender signalisieren.

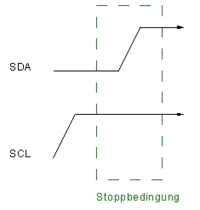
STOP-Bedingung

Das Gegenstück zu der Start-Bedingung ist die Stop-Bedingung. Diese wird erzeugt, indem die SDA Leitung von LOW auf HIGH wechselt, während sich die SCL Leitung in der HIGH Phase befindet. Diese Bedingung wird ebenfalls durch den Master erzeugt. Eine bestimmte Zeit nach dem STOP befindet sich die Bus-Leitung im freien Zustand.

Abb. 8: START-Bedingung

Abb. 9: Adressierung und R/W

Abb. 10: Acknowledge/Not Acknoledge

Abb. 11: STOP-Bedingung

Herstellung der Kommunikation

Abb. 12: Herstellung der Kommunikation

In diesem Projekt wird der Temperatursensor zunächst durch einen Arduino angesteuert und ausgelesen. Im weiteren Schritt werden die Daten über eine serielle Schnittstelle an Matlab gesendet und dort weiter verarbeitet.

Anschluss an Arduino

Abb. 14: Arduinoanschluss Schaltplan

Abb. 13: Sensor-Arduino-Verbindung

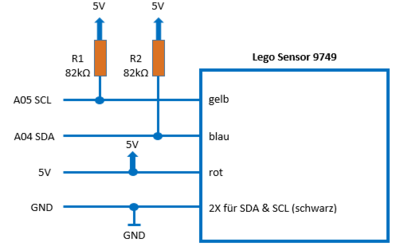
Der Sensor besitzt eine I²C Schnittstelle. Es gibt zwei Möglichkeiten die Kommunikation zwischen dem Sensor und dem Arduino herzustellen. Bei der ersten Möglichkeit kann man den I²C Bus aufschneiden und die einzelnen Kabel mit dem Arduino und den Widerständen verbinden. Da wir aber zerstörungsfrei arbeiten möchten, wird ein Connector Kit for NXT or EV3 genutzt. Mit diesem Connector ist es möglich, den I²C Bus mit dem Arduino zerstörungsfrei zu verbinden. Zur Hilfe wird ein Steckbrett hinzugezogen. Zur Verbindung werden 4 Kabel und 2 Widerstände benötigt.

1. Das blaue Kabel stellt die SDA-Leitung dar. Dafür wird das Kabel mit dem Port A4 des Arduinos verbunden.
2. Das gelbe Kabel stellt die SCL-Leitung dar. Dafür wird das Kabel mit dem Port A5 des Arduinos verbunden.
3. Das rote Kabel liefert die Spannung von 5 Volt und wird somit an die 5V des Arduinos angeschlossen.
4. Der I²C Bus besitzt zwei Grounds, die miteinander verbunden und über das schwarze Kabel an das GND des Arduinos angeschlossen werden.
5. Zum Schluss werden zwei Pull-Up Widerstände von 82kOhm benötigt. Einer davon wird zwischen die Spannungsversorgung und der SDA-Leitung und der andere zwischen Spannungsversorgung und der SCL-Leitung geschaltet.
   
   

Sensor-Arduino-Kommunikation

Um die Kommunikation zwischen dem Arduino und dem Sensor zu realisieren, wird die Adresse des Sonsors benötigt. Dies ist auf mehreren Wegen möglich.

Die erste Möglichkeit besteht darin die Adresse auszulesen. Hilfreich dabei ist der Logic Analyzer. Mit dem Gerät wird die SDA- und SCL-Leitung angeklemmt und die Informationen des Sensors ausgelesen. Der Logic Analyser erkennt die Bitmuster und liefert unter anderem die Adresse des angesprochenen Sensors (siehe Abb. 15).

Abb. 15: SDA-SCL-Signale - Logic Analyzer

Hat man das Gerät nicht zur Verfügung, so muss recherchiert werden, ob sich jemand mit dem Sensor bereits auseinander gesetzt hat.

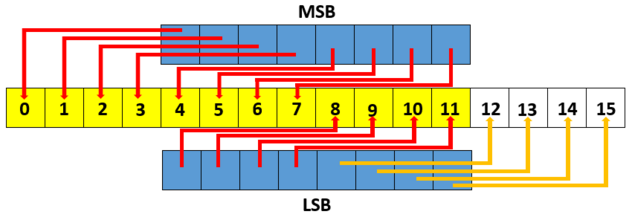
Ist die Adresse vorhanden, wird der Arduino so programmiert (Programm befindet sich unten), dass dieser als Master von dem Sensor ständig Werte (Signale) anfordert. Da es sich um eine I²C Kommunikation handelt, wird die sogenannte Wire-Bibliothek benötigt. Die Informationen über die Temperatur werden jeweils in 2 Bytes versendet. Der erste Byte ist der wichtigste und wird MSB (Most Significant Byte) genannt. Darauf folgt der LSB (Least Significant Bit). Insgesamt sind es also 16 Bits die gesendet werden. Da der Sensor aber nur einen 12 Bit AD Wandler hat, werden nur 12 Bits verwertet. Aus diesem Grund wird Bit-Shiften verwendet. Durch das Bit-Schiften werden die beiden Bytes so angeordnet, dass der MSB vollständig vorhanden bleibt während der LSB durch den Bit-Shift halbiert wird (siehe Abb.16). Am Ende des Programms wird ein Dezimaler Wert ausgegeben, der in Matlab weiterverarbeitet werden soll.

Abb. 16: MSBplusLSB

//Bibliothek für die I²C Kommunikation
#include <Wire.h>
//Adresse des Sensors          
#define ADDR 0x4C            
//Deklaration der Speichervariablen für die Temperatur
byte msb; //erste Byte ist MSB (höherwertig)
byte lsb; //zweiter Byte ist LSB (niederwertig)
int Rohwert;
 
void setup() 
{
  Serial.begin(9600);
  Wire.begin();
}
 
void loop() 
{
//Jetzt werden 2 Bytes vom Sensor angefordert. Zuerst kommt der MSB (hochwertige Byte) und dann der LSB (der niedrigwertige Byte).
  Wire.requestFrom(ADDR, 2);
  if(Wire.available() >= 2)
  {
    msb = Wire.read(); //erste Byte ist MSB (höherwertig)
    lsb = Wire.read(); //zweiter Byte ist LSB (niederwertig)
    
 /* Da der Sensor aber nur 12 Bits verarbeiten kann, muss mit Bitshifts gearbeitet werden, um die 16 Bits in 12 Bits umzuwandeln.
  * Der MSB muss dabei vollständig erhalten bleiben, während der LSB "gekürzt" werden kann.
  * Der MSB wird um 4 Stellen nach links geshiftet und der MSB um 4 Stellen nach rechts und wird dem MSB hinzugefügt. 
  * Der Arduino liest aber nur die ersten 12 Bits, der Rest wird abgeschnitten.
  */
 
    Rohwert = ((msb)<<4); //Der MSB wird um 4 Bits nach links verschoben.
    Rohwert |= (lsb>>4);  //Der LSB wird um 4 Bits nach rechts verschoben und zu dem MSB hinzuaddiert.
    Serial.println(Rohwert);
  }
  delay(100);
}

Weiterverarbeitung der Daten in Matlab

Die vorverarbeiteten Daten, werden weiter an Matlab gesendet, dort mit der Auflösung von 0,0625 multipliziert und geplotet. Das Programm für Matlab befindet sich unten.

clear all
clc;
Object=serial('COM5','BaudRate', 9600, 'DataBits',8);
fopen(Object);

f = figure; 
set(f, 'Position', [100, 0, 1200, 1100])

xArry = 1:1:1001;
yArry = zeros(1,1001);

for t = 1:1:1001
   
    yArry(1,t) =  str2num(fgetl(Object))*0.0625;
    
    plot(xArry, yArry);
    grid on;
    
    Ticks = 0:100:1000; 
    set(gca, 'XTickMode', 'manual', 'XTick', Ticks, 'xlim', [0,1000]);
    Ticks = 0:1:71;
    set(gca, 'YTickMode', 'manual', 'YTick', Ticks, 'ylim', [0,71]);
    xlabel('Zeit in Dezisekunden') 
    ylabel('Temperatur in °C')
    title('Temperaturverlauf')
    axis([0 1000 0 71]);
    
    
    pause (0.01); 
end

fclose(Object);

Messungen und Darstellung der Ergebnisse

In diesem Kapitel werden einige Messungen durchgeführt um zu testen, wie hoch die Genauigkeit des Sensors ist. Wie aus dem Matlabprogramm zu entnehmen ist, werden in den 100 Sekunden insgesamt 1000 Werte (also 10 Signale pro Sekunde) aufgenommen. Die Messversuche werden an Wasser durchgeführt, welches unterschiedlich temperiert wird. Die Messungen werden bei der Raumtemperatur von 23°C durchgeführt.

Trägheit

Abb. 16: Temperaturmessung-Trägheit

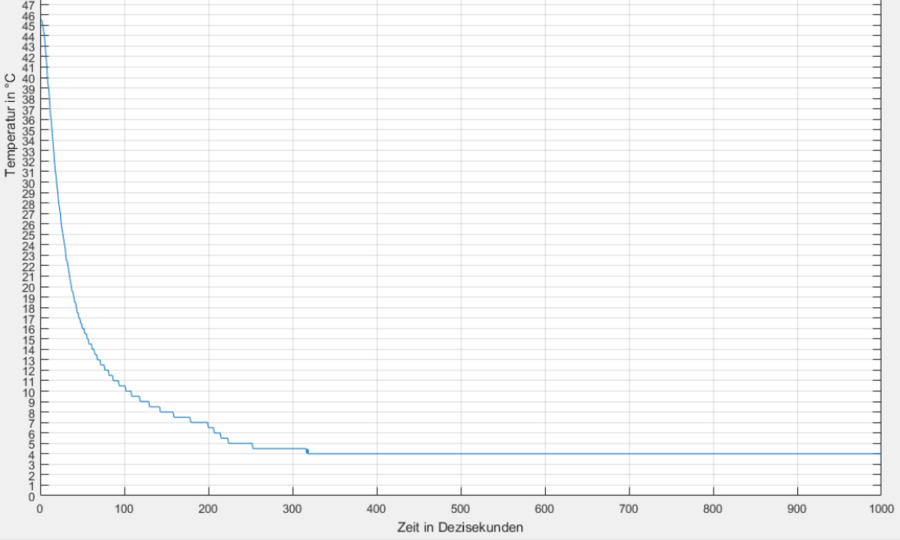
Im Laufe mehrerer Messungen ist aufgefallen, dass der Sensor eine gewisse Zeit benötigt, um sich an die tatsächliche Temperatur, die durch ein Referenzmessgerät gemessen wurde, anzunähern (siehe Abb. 16). Diese Trägheit liegt wahrscheinlich mit der Länge des Fühlerrohrs zusammen und würde im weiteren Verlauf die Mittelwerte der Messreihen negativ beeinflussen. Aus diesem Grund wird der Temperatursensor bei weiteren Versuchen für einige Zeit in das Wasser gelegt, bevor die Messung gestartet wird, um präzisere Werte zu erhalten und bessere Mittelwerte zu ermitteln..

Theorie zur Bestimmung der Messunsicherheit

Es werden einige Parameter und Formeln benötigt, um die Messunsicherheit zu bestimmen.

Mittelwert: Der Mittelwert ${\bar {x}}$ ist eine Schätzung des Erwartungswertes bei einem Stichumfang von n.

$\bar x=\frac{1}{n}\cdot\sum_{i=1}^n x_i$

Standardabweichung: Die Standardabweichung gibt die Streubreite der Messwerte um dessen Mittelwert an.

$s = \sqrt{\frac{1}{n-1}\cdot\sum_{i=1}^n (x_i - \bar x)^2}$

Vertrauensbereich für den Erwartungswert: Damit wird die Messunsicherheit bestimmt.

$u_A = \bar x \pm \frac{t\cdot(n-1)}{\sqrt n}\cdot s$

Ergebnisse der Messungen

Messreihe	"Wahrer Wert"	jeweils 1000 Messungen
Nr.	Referenzwert in °C	Min in °C	Max in °C	Mittelwert	Standardabweichung $s_i$	Messunsicherheit	Vertrauensbereich
1)	2	1,5	2,5	1,86	0,2388	0,0148	1,86 ± 0,0148
2)	12	12	12,5	12,39	0,2047	0,0127	12,39 ± 0,0127
3)	21	22,5	22,5	22,5	0	0	22,5 ± 0
4)	27	28	27	27,3	0,34	0,0211	27,3 ± 0,0211
5)	41	41	42	41,6	0,2567	0,0159	41,6 ± 0,0159
6)	57,5	57	58,5	57,685	0,49	0,0304	57,685 ± 0,0304
7)	67	66	68	67,03	0,52	0,0322	67,03 ± 0,0322

Auswertung der Ergebnisse

Wie bereits erwähnt, ist der Temperatursensor träge, weswegen dieser als erstes in das zu messende Element gelegt und erst nach einer gewissen Zeit gestartet wurde. Auf diese Weise wurden sieben Messreihen durchgeführt. Insgesamt lässt sich sagen, dass die Temperaturwerte der tausend Messungen (pro Messreihe) um bis zu 1,5 °C von dem Referenzwert abgewichen sind, wobei da angenommen wurde, dass die jeweilige Referenztemperatur dem wahren Wert entspricht. Somit ist die Nutzung des Sensors nicht für schnelle und hochpräzise Messungen zu empfehlen. Schaut man sich die Messunsicherheit an, so ist festzustellen, dass sich diese auf die zweite Nachkommastelle auswirkt und somit fast vernachlässigbar ist. Mit dem Hintergrund das dieser Sensor für Lernzwecke und nicht für hochpräzise Temperaturmessung hergestellt worden ist, ist die Präzision der Messungen völlig ausreichend.

YouTubeVideo

https://www.youtube.com/watch?v=2INj0Ovme6A

Quellenverweise

→ zurück zum Hauptartikel: Signalverarbeitende Systeme