Pool-Billard Assistenz: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
[[Kategorie:Projekte]] | [[Kategorie:Projekte]] | ||
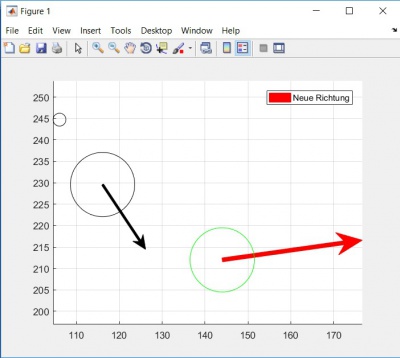
[[Datei:Neue Richtung.jpg|400px|thumb| | [[Datei:Neue Richtung.jpg|400px|thumb|right|Neue Richtung]] | ||
Autoren: [[Benutzer:Christo Tsibadze|Christo Tsibadze]], [[Benutzer:Kevin Penner|Kevin Penner]]<br/> | Autoren: [[Benutzer:Christo Tsibadze|Christo Tsibadze]], [[Benutzer:Kevin Penner|Kevin Penner]]<br/> | ||
Betreuer: [[Benutzer:Ulrich_Schneider| Prof. Schneider]] | Betreuer: [[Benutzer:Ulrich_Schneider| Prof. Schneider]] | ||
Version vom 7. Juni 2016, 20:51 Uhr
Autoren: Christo Tsibadze, Kevin Penner
Betreuer: Prof. Schneider
Aufgabenstellung
Realisierung einer Billard-Assistenz-Software, mit Hilfe von Matlab und dessen Bildverarbeitungs-Tools: Es soll ein "Billard-Assistenz-Software" entwickelt werden, die aus einem Video (oder Live-Cam) Billard Kugel- und Queue -Positionen erkennt und mit einer Algorithmus die Abprallrichtung einer Zielkugel "vorhersagt" (berechnet). Vor dem Schlag soll anhand der Queue- und Kugel-Positionen erkannt werden in welcher Richtung die weiße Kugel geschlagen wird und falls die weiße Kugel einen anderen Kugel trifft, dann in welcher Richtung diese abprallen wird. Die berechnete Richtungen sollen auf dem Video eingeblendet werden. Für die Bildverarbeitung sowie Programmierung wurde MATLAB R2016a verwendet. Eine CAD-Software wurde während der Entwicklung des Algorithmus zur Prüfung der Ergebnisse eingesetzt.
Erwartungen an die Projektlösung
- Sammeln von weiteren Erfahrungen in Bildverarbeitung mit MATLAB
- Umsetzung der in die Vorlesung gewonnenen Kenntnisse in die Praxis
- Tieferer Einblick in die geometrische Physik
- Sammeln von Erkenntnissen durch Problemstellungen
- Erstellung eines spektakulären Videos, welches die Software demonstriert
Plannung
Projektplan
Die Gesamtaufgabe wurde wie folgt aufgeteilt:
- Kevin Penner:
- Automatische Erkennung von Queue- und Kugelpositionen in einer Videoquelle
- sowie Unterscheidung der Kugeln, weiße- oder Zielkugel
- Christo Tsibadze:
- Ein Algorithmus programmieren, der die Schlagrichtung der weißen Kugel berechnet
- Erkennung ob die weiße Kugel nach dem Schlag einen anderen Kugel trifft oder nicht
- Falls die weiße Kugel eine andere Kugel trifft, Berechnung in welcher Richtung die andere Kugel abprallt.
Die Aufgabe ist freiwillig. Zeitlich wurde für das Projekt im 6. Semester je ca. 3 Stunden pro Woche investiert.
Zur Ideenfindung oder Besprechung der Problemlösungsstrategien wurde regelmäßiges Wochen-Meeting gehalten.
Erkennung von Queue- und Kugelpositionen
Erkennung bzw. Ortung der weißen Kugel
blabla bla bla bla Kevinski
Queuepositionserkennung
blabla bla bla bla Kevinski
Erkennung der Positionen der restlichen Kugeln
blabla bla bla bla Kevinski
Algorithmus für Berechnungen
Schlagrichtung weiße Kugel
Da zwei Positionen bekannt sind ( Queue-X, Queue-Y und Weiß-X, Weiß-Y) ist es leicht die Schlagrichtung zu ermitteln.
Einen Vektor aus zwei gegebenen Punkten wird durch Differenzen der X- und Y-Komponenten bebildet.
Je nach Verwendung wird der Vektor normalisiert, hierbei wird der Vektor durch eigene Länge geteilt.
Länge eines Vektors errechnet man durch einen Wurzel von Summe aller Vektorkomponenten in Quadrat.
Einfachheitshalber wird angenommen das mit der Queuespitze immer auf die Mitte der weißen Kugel geschlagen wird.
Sonst wäre das Projekt in verfügbaren Zeitrahmen nicht machbar.
Sortierung nach Entfernung
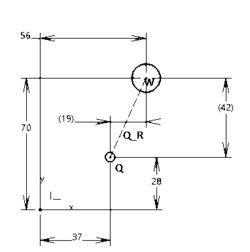
Wenn es in der Schlagrichtung der weißen Kugel mehrere Zielkugel positioniert sind, ist es erforderlich zu unterscheiden welche Kugel näher am weißen Kugel liegt bzw. zuerst getroffen wird. Nach der Kugelpositionserkennung wird eine Matrix bestehend aus 2 Zeilen über gegeben. In der ersten Zeile sind die X-Werte der Kugeln und in zweite die Y-Werte. Anzahl der Spalten ist gleich der erkannten bzw. übrig gebliebenen Zielkugeln. Für die Sortierung nach Entfernung wird der Matrix um eine Zeile erweitert und die bestehenden zwei Zeile werden nach unten geschoben (1. --> 2 und 2. --> 3.). In der ersten Zeile werden für jede Zielkugel die Entfernung zum weißen Kugel berechnet und eingetragen.
Die Entfernung einer Zielkugel zum weißen Kugel wird wie folgt ermittelt:
- Vektorbestimmung anhand der Koordinaten der beiden Kugeln (wie im Schlagrichtung)
- Entfernung: Länge des Vektors bestimmten
Nach dem alle Entfernungen der Zielkugeln in erste Zeile der Matrix eingetragen wurden, wird mit Hilfe der MATLAB-Funktion "sortrows" sortiert.
Diese Funktion ordnet aufsteigend Matrizen nach der ersten Spalte. Da wir nach der ersten Zeile ordnen wollen, wird die Matrix vor dem Sortierfunktion transponiert und nach der Sortierung wieder transponiert.
Beim Transponieren werden die Zeilen und Spalten vertauscht bzw. Zeilen in Spalten und Spalten in Zeilen umgewandelt.
Nach der Sortierung besteht eine Matrix aus drei Zeilen:
- 1. Zeile: Abstände zum weißen Kugel
- 2. Zeile: X-Koordinaten der Zielkugeln
- 3. Zeile: Y-Koordinaten der Zielkugeln
Spaltenanzahl ist gleich Zielkugelanzahl.
Treffer oder kein Treffer
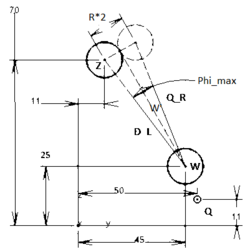
Um herauszufinden ob die weiße Kugel in seiner Schlagrichtung einen Zielkugel trifft, wird wie folgt berechnet. Es wird ein imaginäres gleichschenkliges Dreieck aufgestellt mit folgenden Seitenlängen:
- Länge der kleinen Seite: Kugelradius
- Länge der restlichen beiden Seiten: Entfernung weiß- und ziel Kugel.
Die kleinste Seite wurde mit der Länge Kugelradius gewählt damit die Kugeln sich berühren. Zu bestimmen ist ein Winkel "Max. Winkel" (siehe Bild). Der Max.Winkel liegt zwischen der Schlagrichtung der weißen Kugel Q_R und den direkten Richtung weiß- zu ziel Kugel D_L. Max.Winkel ist abhängig von der Entfernung der Zielkugeln. Wenn der Winkel zwischen der Q_R und der D_L kleiner ist als der Max.Winkel, dann wird diese Zielkugel getroffen, sonst nicht.
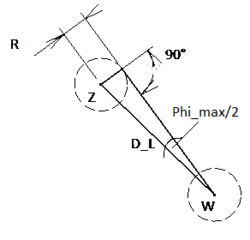
Die Bestimmung von Max.Winkel: zunächst mit rechtwinkliges Dreieck (halbes gleichschenkliges Dreieck)
- D_L: Direkte Linie (Direkte Richtung), zwischen der Ziel- und weißen Kugel ist die Hypothenuse
- Anfangsposition der D_L: Koordinaten der weißen Kugel
- Endposition der D_L : Koordinaten der Zielkugel
- Länge der D_L: Betrag von Vektor zwischen Ziel- und weißen Kugel
- Länge der Gegenkathete: Kugelradius/2
- Winkel zwischen Gegen- und Ankathete: 90°
Da es zwei Seiten und ein Winkel bekannt sind, ist der gesuchte Winkel mit der Sinus-Formel ermittelbar:
Max.Winkel/2 = 2 * asin(Gegenkathete/Hypothenuse)
--> Max.Winkel = 4 * asin(Gegenkathete/Hypothenuse)
Anschließend wird der aktuelle Winkel "Alpha" zwischen den D_L- und Q_R Vektoren wie folgt berechnet:
Ist der Winkel Alpha kleiner als Max.Winkel --> Treffer, sonst kein Treffer.
Falls Treffer: Abprallrichtung
Dem Algorythmus nach wird erst geprüft ob die ziel Kugel mit kleinsten Entfernung zum weißen Kugel mit aktuellen Queue-richtung getroffen wird oder nicht, falls nicht dann wird die ziel Kugel mit nächst kleinsten Entfernung geprüft bis eine Zielkugel gefunden wird der mit getroffen wird. Ist eine Zielkugel gefunden der getroffen werden kann, dann wird versucht die Abprallrichtung der Zielkugel zu berechnen.
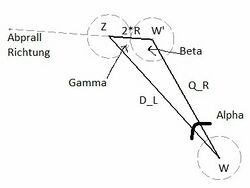
Bekannt sind:
- D_L: die Direkte Linie zwischen den weißen- und ziel Kugel
- Länge, Richtung und Position
- Q_R: die Schlagrichtung der weißen Kugel
- Startpunkt (weiße Kugel), Richtung, keine Länge
- Alpha: Winkel Alpha ist ermittelbar durch zwei Vektoren ( D_L & Q_R)
- 2*R: Richtung zwischen den Zielkugel und den weißen Kugel beim aufprall
- Länge = 2 mal Kugelradius, ein Festpunkt bei Zielkugel
Gesucht: Überschneidungspunkt von 2*R und Q_R und der Winkel in diesem Dreieckspunkt.
Trigonometrisch gesehen sind Zwei lange Seiten des Dreiecks bekannt und der Winkel zwischen diesen Seiten. Also ist es möglich mit Hilfe des Kosinus-Satzes die restlichen Parameter herauszurechnen.
Siehe folgende Quelle: Berechnung eines beliebigen Dreiecks
Sind alle Winkeln bekannt, dann ist der Winkel der sich im Position von Z (Zielkugel) befindet relevant für die Bestimmung von Kugelabprallrichtung. Denn genau um diesen Winkel muss die Richtung D_L rotiert werden um den Kugelabprallrichtung zu bekommen.
Die Rotation einer Linie bzw. Vektor ist mit Multiplikation dessen mit einem Rotationsmatrix möglich.
Fallunterscheidungen
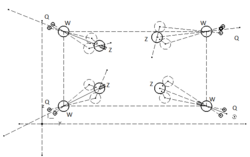
Die korrekte Abprallrichtung der Zielkugel zu berechnen ist es notwendige verschiedene Fälle zu unterscheiden.
Wird der Zielkugel von:
- links nach rechts
- rechts nach links
- oben nach unten
- unten nach oben
und Treffer auf linke oder rechte Hälfte der Zielkugel...
Je nach Kugel-Anordnung ist im Rotationsmatrix entweder negative oder positive Alpha einzugeben.
Deshalb wurde im CAD eine Skizze erstellt und alle Fälle durchgeprüft und die Software angepasst.
Dokumentation
Video
Hier wird ein Link zum Youtube bereitstehen wenn das Video fertig ist.
Fazit
Die von uns angestrebte Ziele wurden erreicht!
- ... hat sehr viel Spaß gemacht.
- ...Die kreative Idee
- Eigenkritik: BLALALALLLALALBLALALABLABLABLA
- Mit mehr zeitlichen Ressource wären in diesem Projekt weitere Ziele denkbar:
- Eingelocht oder nicht
- Kugelabprall an den Banden
- Berechnung ob die getroffene Kugel weiteren Kugeln trifft und ob diese nochmals weitere Kugeln treffen und dessen Richtungen visualisieren.
- ...
Ende gut, alles gut :)
→ zurück zum Hauptartikel: DSB SoSe2016