Grove - Wassersensor: Unterschied zwischen den Versionen

Version vom 26. Juli 2024, 12:29 Uhr

Autor:	Denim Hilz
Studiengang:	Business and Systems Engineering
Modul:	BSE-M-2-1.03, Hausarbeit in Angewandte Informatik gehalten von Prof. Dr.-Ing. Schneider
Semester:	Sommersemester 2024
Abgabetermin:	28.07.2024

Einführung

Aufgabenstellung

In diesem Artikel wird der Grove Water Sensor näher erläutert, die Implementierung in Matlab/Simulink aufgezeigt und die Kalibrierung und Filterung vorgestellt. Der Grove Water Sensor dient zur Erkennung von Wasser und zur Messung des Wasserstands. Einsatzbereiche sind unter anderem das Aufspüren von Wasserlecks, die Steuerung automatischer Bewässerungssysteme, die Überwachung des Wasserstands in Behältern, die Detektion von Flüssigkeiten in Maschinen sowie die Überwachung unerwünschten Wassers in Smart Home Systemen. ^[1]

Anforderungen

Tabelle 1: Anforderungen
Req.	Beschreibung	Priorität
1	Der Niederschlag muss mittels Wassersensor, Arduino und Simulink gemessen werden.	1
2	Der Messbereich muss bestimmt werden.	1
3	Die Messunsicherheit (1σ) muss für den Messbereich ermittelt und als Vertrauensbereich angezeigt werden.	1
4	Der Sensor muss kalibriert werden.	1
5	Für den Messbereich muss der Niederschlag referenziert werden.	1
6	Die Messwerte müssen über der Zeit gefiltert werden.	1
7	Ein Piepton muss anzeigen, wenn der Messwert stabil/konstant ist und Niederschlag erkannt wurde.	1
8	Das Sensorsystem muss eine Regenwarnung auf dem LCD-Display anzeigen.	2

Thema/Fragestellung: Feststellen ob es zum gegenwärtigen Zeitpunkt Niederschlag gibt mittels des Grove Water Sensor.
Hypothese: Niederschlag lässt sich über den Grove Water Sensor feststellen.
Einordnung in den Lehrplan: Die im Modul Angewandte Informatik vermittelten Lernziele, werden im Rahmen dieses Praxisbeispiels angewendet. Folgende Lernziele gilt es dabei zu überprüfen.
- mit der Versionskontrolle SVN nachhaltig Quelltext entsprechend der Programmierrichtlinien schreiben, sichern, kollaboriert bearbeiten und Konflikte lösen.
- in einer mathematisch orientierten Systax (z. B. MATLAB®) mit Vektoren und Matrizen rechnen, Programmteile in Funktionen auslagern, Zweige und Scheifen programmieren, Daten importieren und visualisieren.
- die Mikrocontrollerplattform Arduino modellbasiert mit Simulink programmieren, so dass Sensoren eingelesen und Aktoren angesteuert werden können. ^[2]

Projektbeschreibung

In diesem Abschnitt werden die verwendeten Komponenten vorgestellt.

Tabelle 2: Materialliste
#	Anzahl	Material
1	1	PC mit MATLAB/Simulink R2023b
2	1	Arduino Uno R3
3	1	Grove Water Sensor
4	1	Streckbrett
5	1	Buzzer
6	5	LCD Display
7	2	LED
8	10	Jumper Kabel, männlich/männlich, 20 cm

Beschreibung der verwendeten Hard- und Software

Simulink R2023b

Simulink ist eine grafische Entwicklungsumgebung, die zur MATLAB-Software von MathWorks gehört. Sie dient vor allem der Modellierung, Simulation und Analyse dynamischer Systeme. In diesem Praxisbeispiel dient Simulink der Verarbeitung der Sensordaten. ^[3]

Arduino Uno R3

Der Arduino Uno R3 ist ein beliebtes Mikrocontroller-Board für Elektronikprojekte, basierend auf dem ATmega328P mit 32 KB Flash-Speicher. Es bietet 14 digitale Ein-/Ausgänge, von denen 6 PWM-fähig sind und 6 analoge Eingänge. Der Uno wird über USB oder eine externe Quelle betrieben und lässt sich einfach über die Arduino IDE in C/C++ oder über Matlab/Simulink programmieren.^[4]

Grove Water Sensor

Der Grove Water Sensor wird eingesetzt, um Wasserpräsenz und -stand zu erfassen. Er findet in verschiedenen Bereichen Anwendung:

Wasserleckerkennung: In Haushalten, Büros und industriellen Umgebungen hilft der Sensor, Wasserlecks aufzuspüren und dadurch Schäden durch undichte Stellen zu verhindern.
Automatisierte Bewässerungssysteme: In der Landwirtschaft und Gartenpflege misst der Sensor den Bodenfeuchtigkeitsgehalt und steuert automatische Bewässerungssysteme.
Füllstandsmessung: Der Sensor überwacht den Wasserstand in Behältern, Tanks oder Reservoirs und verhindert Überlauf oder Trockenlauf.
Flüssigkeitserkennung in Maschinen: In industriellen Anwendungen überwacht der Sensor den Flüssigkeitsstand in Maschinen oder Systemen, um einen sicheren Betrieb zu gewährleisten.
Smart Home Anwendungen: In Smart Home Systemen sendet der Sensor Alarme oder Benachrichtigungen, wenn unerwünschtes Wasser erkannt wird, beispielsweise im Keller oder in der Küche. ^[5]

Steckbrett

Ein Steckbrett ermöglicht die Verbindung elektrischer Bauelemente ohne Löten. Es ist in horizontale und vertikale Reihen unterteilt, in denen die Bauteile miteinander verbunden sind. Im Gegensatz zu Leiterplatten werden die Komponenten bei Steckbrett nicht gelötet, sondern in Federkontakte gesteckt. Dadurch kann die Schaltung einfach durch Umstecken angepasst werden. ^[6]

LCD Display

Das I2C 1602 LCD Modul hat ein zweizeiliges Display, das jeweils 16 Zeichen pro Zeile anzeigen kann, und ist mit einem I2C Modul HW-061 auf der Rückseite ausgestattet. Es benötigt eine Taktverbindung (SCL), eine Datenverbindung (SDA) sowie +5VDC und GND. Das Display kann über den I2C-Bus mit lediglich vier Anschlusskabeln betrieben werden. ^[7]

Piezo-Lautsprecher Ein Piezo-Lautsprecher ist ein elektronisches Bauteil, das Schallwellen erzeugt, indem es die piezoelektrischen Effekte nutzt. Dabei wird an ein piezoelektrisches Material, ein Spannung angelegt. Dadurch dehnt sich das Material aus und zieht sich zusammen. Diese Verformung erzeugt Schallwellen, welche als Geräusche oder Töne wahrgenommen werden.

Funktionsweise des Grove Water Sensor

Der Grove-Wassersensor gehört zu dem Grove-System und misst die Leitfähigkeit, um den Feuchtigkeitszustand des Sensors anzuzeigen, also ob der Sensor trocken, feucht oder vollständig in Wasser eingetaucht ist. Der Sensor hat mehrere parallele Leiterbahnen, die auf einem PCB (Printed Circuit Board) aufgebracht sind. Die Sensorkontakte verfügen über einen 1 MΩ Widerstand, der den Sensorwert hochhält. Fällt ein Wassertropfen auf Leiterbahnen, dann werden in dem betroffenen Bereich die Leiterbahnen durch das Wasser überbrückt und der Stromkreis zwischen dem Sensorsignal und GND geschlossen. Umso mehr Leiterbahnen vom Wasser bedeckt sind, umso mehr sinkt der Widerstand. Damit kann dann bestimmt werden ob der Sensor trocken, feucht oder vollständig in Wasser eingetaucht ist. Der Sensor kann dabei sowohl mit den digitalen I/O-Pins, wie auch den analogen Pins des Arduino genutzt werden. ^[9]

Technische Daten

Tabelle 3: Sensordaten ^[10]
Messbereich	0 V - 5 V
Versorgungsspannung	5 V
Versorgungsstrom	20 mA
Arbeitstemperatur	10 °C - +30 °C
Abmessungen	20 mm x 20 mm x 10 mm

Pinbelegung

Tabelle 4: Pinbelegung bei dem Sensor ^[11]
Pin	Belegung	Signal
1	Masse (GND)	0 V
2	Versorgungsspannung VCC	5 V
3	Not Connected (NC)	-
4	Analog Output (SIG)	0 V - 5 V

Versuchsaufbau und Durchführung

Versuchsaufbau

Der Versuchsaufbau wird durch einen Anschlussplan (Abbildung. 3) und einem Foto des Aufbaus (Abbildung. 4) dokumentiert.

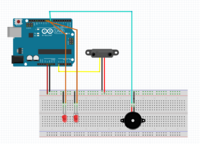
Sensor
Der Sensor wird mit dem Arduino über drei Kabel verbunden. Der VCC Anschluss des Sensors wird mit den 5V Versorgungsspannung des Arduinos und GND des Sensors mit GND des Arduinos verbunden. Der Kontakt SIG wird an den analogen Port (A0) angeschlossen.
Buzzer
Der negative Ausgang des Buzzers wird an GND angeschlossen. Der positive Ausgang wird mit dem digitalen Pin (A8) das Arduino verbunden.
LED Zur visuellen Anzeige ob Niederschlag gemessen wird, sind zwei LEDs angeschlossen. Die grüne LED leuchtet solange kein Niederschlag gemessen wird und ist über GND und den den digitalen Port A9 angeschlossen. Die rote LED leuchtet sobald es regnet und ist über GND und den digitalen Port A10 angeschlossen.

Versuchsdurchführung

Der Sensor soll den Niederschlag zuverlässig messen und feststellen ob es regnet. Dazu wurde der Sensor in eine Halterung geschraubt, die es ermöglicht von oben Wasser darauf tropfen zu lassen. Der Zweck der Halterung ergibt sich aus der Anforderung Niederschlag zu simulieren. Die Halterung setzt sich dabei aus zwei Teilen zusammen. So kann der Sensor flach hingelegt werden, um einzelne Wassertropfen zu messen, oder in den Ständer gesteckt werden, damit das Wasser nach unten abläuft, um Niederschlag simulieren zu können. Die Halterung, zu sehen in Abbildung ?? und Abbildung ??? wurde dabei in Autodesk Fusion360 selbst modellierte und mit einem 3D-Drucker ausgedruckt. Die STL. Datei kann im „Anhang“ heruntergeladen werden.

Abb. ??: Sensor Halterung (verbunden)
Abb. ??: Sensor Halterung (getrennt)

Simulink Modell

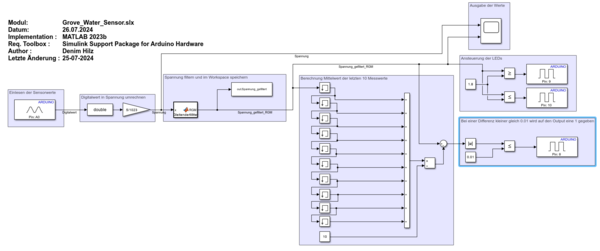
Das in Matlab/Simulink erstellte Modell zur Verarbeitung der vom Sensor gelieferten Daten ist in Abbildung ?? zusehen. Die Sensorwerte werden über den analogen Eingang A0 eingelesen und von dem Digitalwert in eine Spannung umgerechnet. Der 10-Bit-Digitalwert (0 bis 1023) wird vom ADC des Arduino mit einer Referenzspannung von 5V erfasst.

Um den Digitalwert in Volt umzuwandeln, wird er durch 1023 geteilt und mit 5 multipliziert:
$Signal (V) = \frac{Digitalwort \cdot 5V}{1023}$

In Simulink wird dies durch einen Gain-Block erreicht, der den ADC-Wert mit $\frac{5V}{1023}$ multipliziert

Die Spannung wird dann über einen rekursiven gleitenden Mittelwertfilter gefiltert. Aus dem gefilterten Signal wird der Mittelwert der letzten 10 Werte berechnet. Der Mittelwert wird dann an den digitalen Output A8 gegeben. Über den digitalen Output A9 wird eine 1 gegeben wenn der gefilterte Wert größter gleich 1.8V liegt und eine 0 wenn der Wert kleiner als 1.8V ist. Über den digitalen Output A10 wird eine 0 gegeben wenn der gefilterte Wert größter gleich 1.8V liegt und eine 1 wenn der Wert kleiner als 1.8V ist.

Modelleinstellungen:

Hardware Board: Arduino Uno
Type: Fixed-step
Solver: ode1 (Euler)
Abtastrate: 0,001 s

Filterung der Messdaten

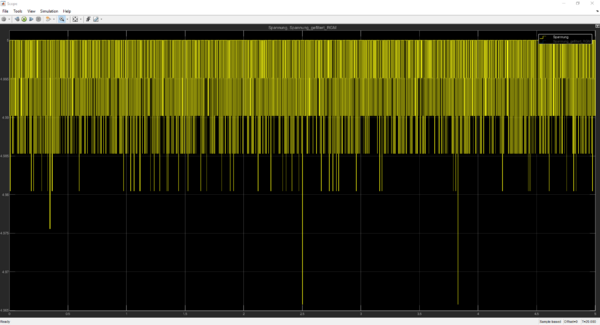
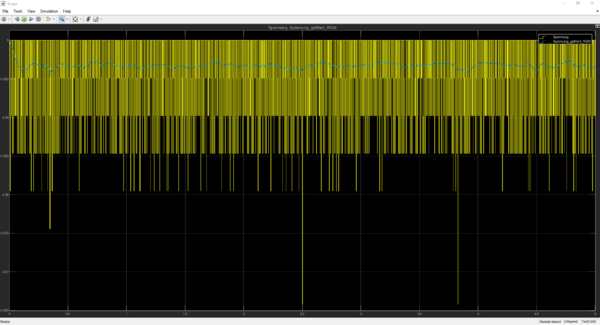
Bevor der Messbereich festgelegt werden kann, muss geschaut werden wie die Sensorkennlinie aussieht und ob Sie ein hohes Rauschen aufweist. Abbildung ?? zeigt das ungefilterte Signal des Sensors in Gelb im trockenen Zustand für 5 Sekunden. Die Sensorkennlinie zeigt dabei deutlich Messausreißer auf, welche gefiltert werden müssen.

Für die Filterung wurde eine rekursiver gleitender Mittelwertfilter eingesetzt. Der Filter wurde in der Lehrveranstaltung "Signalverarbeitende Systeme" behandelt. Bei der Auslegung eines rekursiven gleitenden Mittelwertfilters muss die Fensterbreite, also die Anzahl der in die Berechnung einbezogenen Datenpunkte, festgelegt werden. Eine größere Fensterbreite verbessert die Filterung des Rauschens, was zu einer glatteren Kurve führt. Allerdings nimmt mit einer größeren Fensterbreite auch die zeitliche Verzögerung des gefilterten Signals zu, weil mehr vergangene Datenpunkte berücksichtigt werden müssen. Es ist somit wichtig, einen Kompromiss zwischen der Qualität der Filterung und der zeitlichen Verzögerung des gefilterten Signals im Vergleich zum Originalsignal zu finden.
Die Fensterbreite für diesen Sensor wurde auf 80 festgelegt. Somit erhält man ein geglättetes Signal, mit einer geringen zeitlichen Verzögerung. Da der Sensor nicht in harten Echtzeitsystemen zum Einsatz kommt, ist eine geringe zeitliche Verzögerung hinnehmbar. Das gefilterte Signal des Sensors in Blau im trockenen Zustand für 5 Sekunden ist in Abbildung ?? zu sehen.

Mabtlab Code des rekursiven gleitenden Mittelwertfilters:

function RGM = RekGleitenderMittelwert(x)
persistent n aSchieberegister
persistent bErsterDurchlauf
if isempty (bErsterDurchlauf)
    n = 80;
    aSchieberegister = x * ones (n,1);
    bErsterDurchlauf = 1;
end
for m=1:n-1
    aSchieberegister (m) = aSchieberegister(m+1);
end
aSchieberegister (n) = x;
RGM = x;
RGM = sum(aSchieberegister) / n;
end

Messbereich

Für die Bestimmung des Mess und Vertrauensbereich, wurde geschaut welche Werte der Sensor im trocknen Zustand hat und welche Werte vorliegen sobald Wassertropfen auf den Leiterbahnen liegen. Dafür wurden drei Zustände definiert.

1. "Zustand Trocken": Es liegt kein Wasser auf den Leiterbahnen des Sensors
2. "Zustand Nass": Es liegt ein Wassertropfen auf den Leiterbahnen des Sensors
3. "Zustand Niederschlag": Es tropfen kontinuierlich Wassertropfen auf den Leiterbahnen des Sensors

Für die Überprüfung der Zustände wurde das gefilterte Signal benutzt.

Zustand Trocken

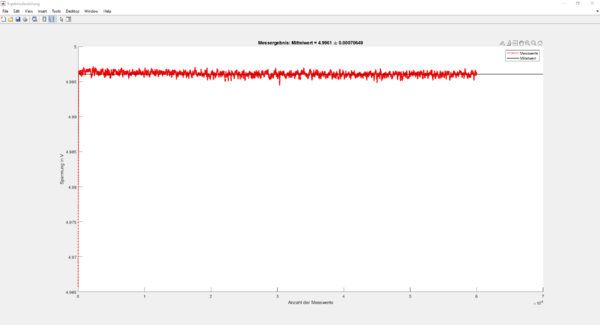
Wenn der Sensor trocken ist, also kein Wasser auf den Leiterbahnen liegt, hat der Sensor ohne Filterung ein ziemlich hohes Rauschen. Mit der Filterung über einen rekursiven gleitenden Mittelwertfilter, gibt der Sensor ziemlich konstant fast 5V aus. Es finden keine großen Messausreißer statt, so dass zuverlässig bestimmt werden kann, wenn kein Niederschlag stattfindet. Abbildung ?? zeigt das gefilterte Signal über 60 Sekunden. Über eine Matlab Funktion wurde daraus der Mittelwert und der Abweichung vom Mittelwert berechnet (Abbildung ??). Es zeigt sich, dass das gefilterte Signal sehr konstant ist und eine Abweichung von gerade einmal $\pm 0.00070649V$ hat.

Matlab Funktion zur Berechnung des Mittelwertes:

%% Mittelwert berechnen
%% Daten aus Simulink extrahieren
Spannung = Spannung_gefiltert;
Messwerte = length(Spannung)
%% Mittelwert der Spannung
MSpannung = mean(Spannung)  % Mittelwert
sE = std(Spannung);         %Standardabweichung
%% Ergebnisplot
h = figure;
set(h, 'Name', 'Ergebnisdarstellung', 'NumberTitle', 'off');
xlabel('Anzahl der Messwerte')
ylabel('Spannung in V')
hold on
p1 = plot(Spannung,'r.-');
p2 = yline(MSpannung, 'LineWidth', 2);
title(['Messergebnis: Mittelwert = ', num2str(MSpannung), ' \pm ', num2str(sE)])
% Legende einfügen
h = legend([p1, p2], "Messwerte", "Mittelwert", 'Location', 'northeast');
hold off

Zustand Nass

Um zu schauen ab wann der Sensor Niederschlag erkennt, wurde ein Wassertropfen auf die Leiterbahnen getropft und die Messdaten für 5 Sekunden aufgezeichnet. Über oben aufgeführte Matlab Funktion, wurde dann aus den aufgezeichneten Messwerten wieder der Mittelwert berechnet. Der ganz Vorgang wurde 10 mal wiederholt, wobei der Wassertropfen jedes Mal auf eine anderen Stelle auf der Leiterbahn getropft wurde. So soll ein möglichst realitätsnahes Ergebnis erzielt werden, da Regentropfen nicht immer an der gleichen Stelle aufschlagen.

Folgende Werte wurden dabei aufgezeichnet:

01. Durchlauf: 0.85378
02. Durchlauf: 0.90942
03. Durchlauf: 0.81612
04. Durchlauf: 1.03845
05. Durchlauf: 1.45663
06. Durchlauf: 0.74349
07. Durchlauf: 0.95096
08. Durchlauf: 1.01804
09. Durchlauf: 1.79295
10. Durchlauf: 1.01497

Der Mittelwert aus den 10 Durchläufen beträgt somit $x = \frac{0.85378+0.90942+0.81612+1.03845+1.45663+0.74349+0.95096+1.01804+1.79295+1.01497}{10}= 1.05948$

Wichtig zu erwähnen ist, dass die Wassertropfen nicht alle gleichgroß sind. Während bei größeren Tropfen Werte von 0.7V - 0.8V aufgezeichnet werden konnten, erzielten kleine Wassertropfen Werte zwischen 1.4V und 1.8V. Der Messbereich von Niederschlag liegt somit bei unterhalb 1.8V.

Zustand Niederschlag

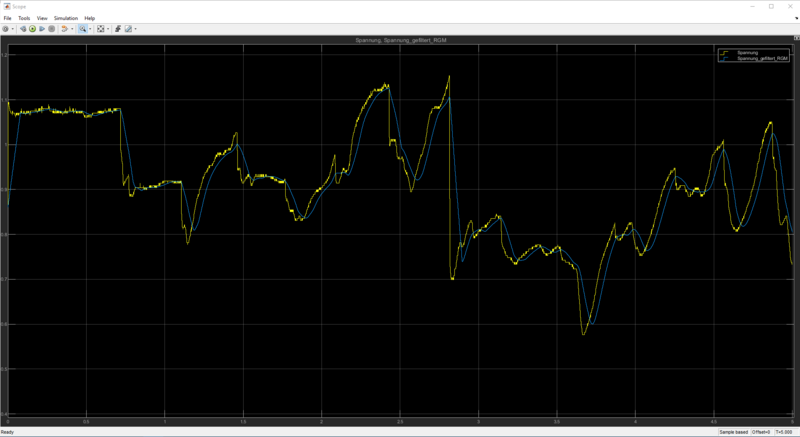
Nachdem der Bereich bestimmt wurde in dem der Sensor Niederschlag misst, wurde eine Niederschlagssimulation über 5 Sekunden durch geführt. Dabei wurde von Beginn der Simulation bis zum Ende Wassertropfen auf die Leiterbahnen gegeben. Abbildung ??? zeigt die aufgezeichnet Sensorkennlinie:

Anhand der Sensorkennlinie sieht man, dass der Wert unterhalb den 1.8V liegt, die zuvor als Grenzwert für Niederschlag festgelegt wurden. Die einzelnen Peaks treten auf wenn ein weitere Wassertropfen dazu kommt (Negative Steigung), ein Wassertropfen die Leiterbahnen entlang fließt (Abwechselnd leicht negative und positive Steigung) oder wenn ein Wassertropfen von Sensor fließt und der Kontakt zwischen den Leiterbahnen unterbrochen wird (Positive Steigung).

Messunsicherheit

Im Folgenden die das Vorgehen zur Bestimmung der Messunsicherheit erläutert. Nachdem der Messbereich ermittelt wurde, muss noch die Messunsicherheit des Sensors bestimmt werden. Hierfür wurde das GUM-Verfahren (Guide to the Expression of Uncertainty in Measurement) angewendet. GUM wurde in der Lehrveranstaltung "Signalverarbeitende Systeme" behandelt wurde. Die Matlab Funktionen zur Berechnung der Messunsicherheiten, wurden aus den Matlab Grader Aufgaben entnommen und auf die Ausarbeitung angepasst. Der Sensor fällt in die Kategorie "Vermessungstechnik". Nach GUM ergibt sich daraus ein Vertrauensniveau von 68,27%, was einer Standardabweichung von 1σ entspricht. Der Vertrauensfaktor wurde mit $k = 2$ festgelegt.

Zum Anzeigen den Vollständigen Matlab Codes muss der Bereich aufgeklappt werden.

%**************************************************************************
%                   Hochschule Hamm-Lippstadt                             *
%**************************************************************************
% Modul	          : Grove_Water_Sensor_MATLAB                             *
%                                                                         *
% Datum           : 25. Juli 2024                                         *
%                                                                         *
% Funktion        : Berechnung des Mess und Vertrauensbereich             *
%                   des Grove-Water-Sensor                                *
%                                                                         *
% Implementation  : MATLAB 2023b                                          *
%                                                                         *
% Req. Toolbox    :                                                       *
%                                                                         *
% Author          : Denimilz                                              *
%                                                                         *
% Bemerkung       :                                                       *
%                                                                         *
% Letzte Änderung : 25-07-2024                                            *
%                                                                         *
%**************************************************************************
%% open('Grove_Water_Sensor')

%% Script überarbeiten

%% Daten aus Simulink extrahieren
Spannung = Spannung_gefiltert;
Messwerte = length(Spannung)

%% Berechnung der Standardunsicherheit

% Mittelwert und Standardabweichung
mS = mean(Spannung);        % Mittelwert
sE = std(Spannung);         %Standardabweichung

% Berechnen der Standardunsicherheit Typ A
alpha = 1 - 0.6827;         % Messunsicherheit mit 68,27% Prozent Aussagesicherheit, da Messtechnnik
p = 1 - (alpha / 2);
t = tinv(p, Messwerte - 1);
uA = sE * t / sqrt(Messwerte);

% Werte des Microprozessors Atmega328p
Uref = 5;                       % Referenzspannung
Aufloesung = 10;                % Auflösung des Atmega328p
Ulsb = Uref / (2^Aufloesung-1)

% Standardunsicherheit Typ B
uB = Ulsb / sqrt(3) 

% Berechnen der Standardunsicherheit Typ C
uC = sqrt(uA^2 + uB^2)  

% Vertrauenfaktor
k = 2;              % Vertrauensniveau 0.9545

% Berechnen der Messunsicherheit 
uAbs = k * uC       % absolute Messunsicherheit 
uRel = 100*(uAbs/mS)  % relative Messunsicherheit

% Vollständiges Messergebnis ausgeben
disp(['Vollständige Messergebnis: U = ', num2str(mS), ' ± ', num2str(uAbs), ' V ']);

h = figure;
set(h, 'Name', 'Ergebnisdarstellung', 'NumberTitle', 'off');
xlabel('Anzahl der Messwerte')
ylabel('Spannung in V')
hold on

p1 = plot(Spannung,'r.-');
p2 = yline(mS, 'LineWidth', 2);
p3 = yline(mS + uC, 'Color', 'blue');
p4 = yline(mS - uC, 'Color', 'blue');
title(['Messergebnis: Mittelwert = ', num2str(mS), ' \pm ', num2str(sE), ' V, Spannung = ', num2str(mean(Spannung)), ' \pm ', num2str(uRel), '%'])

% Legende einfügen
h = legend([p1, p2, p3], "Messwerte", "Mittelwert", "Unsicherheit Typ C", 'Location', 'northeast');
hold off

Abbildung ?? zeigt das Ergebnis der Berechnung.

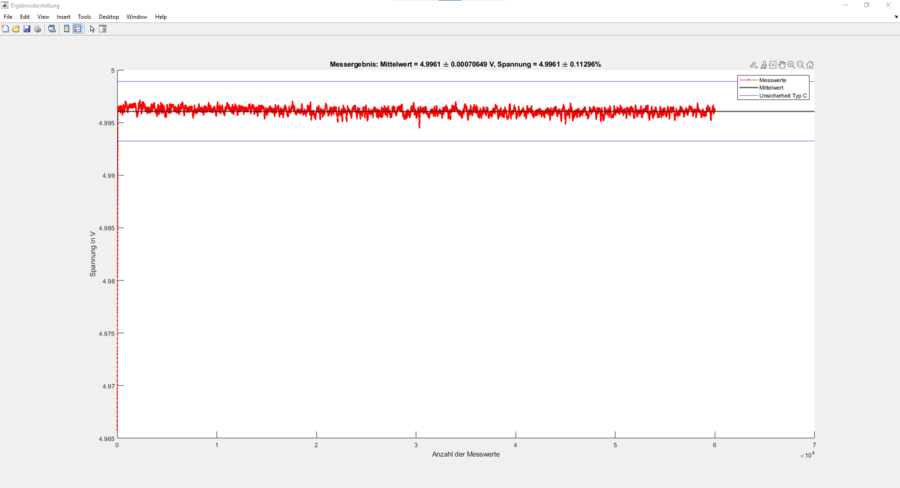
Kalibrierung des Sensors

Der Sensor arbeitet bereits ohne umfangreiche Kalibrierung sehr zuverlässig. Anhand der in Zustand Nass gesammelten Daten wurde gezeigt, dass bei Werten unterhalb 1.8V Niederschlag vorliegt. Somit lässt sich ein Bereich von 5V bis 1.8V festgelegt, in dem kein Niederschlag detektiert wird. Werte unterhalb von 1.8V zeigen das Vorhandensein von Niederschlag an. Mit dieser kleinen Kalibrierung können bereits zuverlässige Ergebnisse hinsichtlich der Niederschlag Erkennung erzielt werden.

Versuchsdurchführung mit einer dynamischen Regen-Simulation

Nachdem der Mess- und Vertrauensbereich bestimmt war, konnte ein umfassender Versuch durchgeführt werden. Der Versuch erstreckte sich über 20 Sekunden. Zu Beginn wurde kein Niederschlag simuliert. Ab der 5. Sekunde wurde Regen simuliert, und ab der 15. Sekunde wurde erneut kein Niederschlag mehr simuliert. Das Ergebnis des Versuchs ist in dem Ergebnisvideo und in der folgenden Abbildung zusehen:

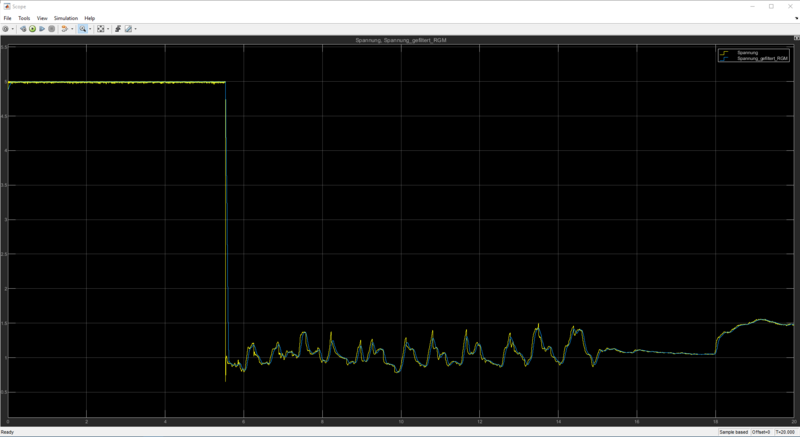
Versuchsbeobachtung

Der Versuch zu der dynamischen Regen-Simulation zeigt, dass der Sensor den Niederschlag zuverlässig misst. Dabei fällt auf, dass die auch ohne Filterung des Signals möglich ist. Der Filter hilft dabei Peaks in den Messwerten abzufangen und zu glätten. Die Messwerte ohne Niederschlag befinden sich sehr nahe an 5V und die Messwerte bei Niederschlag liegen im Mittel bei etwas mehr 1V, was zuvor im Zustand Nass ermittelt wurde. Da sich der Messwert mit jedem neuen Tropfen oder jedem Tropfen der von Sensor fließt teilweise stark verändert, geht der Buzzer immer wieder an und aus. Die lässt sich nicht vermeiden, aufgrund der Unbeständigkeit von Regen. Die angeschlossenen LEDs hingegen, zeigen zuverlässig an wenn keine Niederschlag (Grüne LED leuchtet) und wenn Niederschlag (Rote LED leuchtet) vorliegt.

Auswertung

Die Messhypothese "Niederschlag lässt sich über den Grove Water Sensor feststellen" konnte bestätigt werden. Der Sensor liefert bereits ohne Filterung sehr zuverlässige Ergebnisse, wenn man den Messbereich und die Kalibrierung festlegt. Durch die Filterung des analogen Eingangssignals konnte die Abweichung vom Mittelwert auf $\pm 0.00070649V$ . Die Messunsicherheit beträgt $\pm 0.11296\%$ . Der Niederschlag konnte zuverlässig detektiert und visuell über die beiden LEDs ausgegeben werden. Da der Sensor keine harten Echtzeitanforderungen erfüllen muss ist eine leichte zeitliche Verzögerung aufgrund des Filters hinnehmbar. Gleichzeitig arbeitet der Sensor auch ohne großartige Filterung sehr zuverlässig, weshalb die Messwerte keine hohe Filterung benötigen. Mit einer Fensterbreite von 80, konnte somit ein guter Kompromiss gefunden werden, zwischen einer brauchbaren Filterung der Messwerte und einer kleinen zeitlichen Verzögerung.

Zusammenfassung und Ausblick

Zusammenfassung

Die Sensordaten zeigen, dass der Grove Water Sensor zuverlässig zwischen trockenem Zustand und Niederschlag unterscheiden kann. Werte unterhalb von 1.8V bedeuten es liegt einen Niederschlag vor, während Werte zwischen 1.8V und 5V Aussagen, dass kein Niederschlag stattfindet. Diese Schwellenwerte wurden auf Basis der gemessenen Daten und der Kalibrierung des Sensors festgelegt.

Aus den Werten des Trocken Zustands und den Werten des Nassen Zustands lässt sich somit festhalten, dass gemessene Werte unter halb 1.8V darauf schließen lassen, dass es Niederschlag gibt. Im Bereich von 1.8V bis 5V liegt kein Niederschlag vor. Diese Werte gelten nur für den Fall das ein Wassertropfen auf den Leiterbahnen liegt. Liegen Mehrere Wassertropfen darauf, fallen die Messwerte niedriger aus.

Diskussion der Ergebnisse

Die Sensordaten bestätigen, dass der Grove Water Sensor effektiv zwischen trockenem Zustand und Niederschlag unterscheidet. Die Filterung der Messdaten hat die Genauigkeit verbessert, indem sie Rauschen und Peaks minimiert hat. Es wurde festgestellt, dass kleine Wassertropfen höhere Werte liefern als größere Tropfen, was bei der Kalibrierung berücksichtigt werden muss. Die LEDs haben zuverlässig auf den Niederschlag reagiert. Der Niederschlag konnte somit erfolgreich detektiert werden.

Ausblick

Für zukünftige Arbeiten könnten weitere Verbesserungen der Sensorgenauigkeit erzielt werden, etwa durch eine genauere Kalibrierung oder den Einsatz zusätzlicher Sensorkomponenten. Ebenso wäre es möglich die Niederschlagsmenge zu messen, um gewisse Grenzwerte festlegen zu können wie viel Prozent Niederschlag noch in Ordnung sind und ab wie viel Prozent reagiert werden muss. Zusätzlich könnte die Anwendung des Sensors auf verschiedene Flüssigkeiten ausgeweitet werden, um dessen Vielseitigkeit zu erhöhen. Der Grove Water Sensor ist für die Erkennung von Wasser optimiert. Im Rahmen dieser Ausarbeitung wurde nur mit Wasser gemessen. Interessant wäre es zu sehen wie der Sensor auf andere Flüssigkeiten wie Öl oder Chemikalien reagiert.

Selbstreflexion/Lessons learned

Während der Durchführung dieser Ausarbeitung gab es viele Erkenntnisse und Herausforderungen. Eine der wichtigsten Aufgaben war die Festlegung des Mess- und Vertrauensbereich und die Kalibrierung des Sensors. Somit konnten viele gewonnen Erkenntnisse aus dem Sommersemester 2024 noch einmal praktisch umgesetzt werden. Viele Themen die im Modul Signalverarbeitende Systeme gelehrt wurden, konnten praktisch angewendet und vertieft werden. Zu dem konnte tiefergehend in die Messtechnik und in die Thematik Microcontroller und Arduino eingestiegen werden. Zusammenfassend bildet die Hausarbeit ein gelungenes Zusammenführen von den gelehrten theoretischen und praktischen Inhalten und der Umsetzung in Eigenarbeit

Ergebnisvideo

Video der Versuchsdurchführung

Anleitung: Videos im Wiki einbinden

Lernzielkrontrolle

Beantworten Sie in Ihrem Artikel die Lernzielkontrollfragen.

Lernzielkontrollfragen

Wie funktioniert der Primärsensor technisch?
Welche Leistungsmerkmale hat der Sensor?
Wie funktioniert die Umsetzerschaltung technisch?
Wie kommuniziert der Sensor mit dem Arduino?
Muss der Sensor kalibriert werden?
Wie wird der Messwert in die zu messende physikalische Größe umgerechnet?
Was nutzen Sie als Referenz?
Benötigt der Sensor eine Kennlinie?
Welchen Messbereich hat das Signal am Ende der Messkette?
Welche Messunsicherheit und welcher Vertrauensbereich hat das Signal am Ende der Messkette für den gesamten Messbereich?
Welche Auflösung hat das Signal am Ende der Messkette? Wodurch wird die Auflösung bedingt?
Weist das Signal am Ende der Messkette einen systematischen oder zufälligen Fehler auf?
Welche Fehlereinflüsse hat die Messung? Muss z. B. die Temperatur der Messung berücksichtigt werden?

Literatur

Zitieren Sie nach DIN ISO 690:2013-10.

Anhang

STL-Datei Sensorhalterung: Datei:Grove Water Sensor Halterung.stl
Simulink-Modell:

Datenblätter
Simulink-Modell
Originaldateien (PAP, Schaltplan,... )

→ zurück zum Hauptartikel: BSE Angewandte Informatik SoSe24 | Hausarbeit SoSe24

↑ https://cdn-reichelt.de/documents/datenblatt/A300/101020018_01.pdf, abgerufen am 14.07.2024
↑ https://wiki.hshl.de/wiki/index.php/BSE_Angewandte_Informatik_-_SoSe24, abgerufen am 14.07.2024
↑ https://de.mathworks.com/products/simulink.html, abgerufen am 14.07.2024
↑ https://docs.arduino.cc/hardware/uno-rev3/, abgerufen am 14.07.2024
↑ https://cdn-reichelt.de/documents/datenblatt/A300/101020018_01.pdf, abgerufen am 14.07.2024
↑ https://wiki.hshl.de/wiki/index.php/Steckbrett, abgerufen am 14.07.2024
↑ https://wiki.hshl.de/wiki/index.php/LCD_Modul_16x02_I2C, abgerufen am 14.07.2024
↑ https://wiki.seeedstudio.com/Grove-Water_Sensor/
↑ https://www.mouser.com/datasheet/2/744/Seeed_101020018-1217524.pdf, abgerufen am 21.07.2024
↑ https://cdn-reichelt.de/documents/datenblatt/A300/101020018_01.pdf, abgerufen am 14.07.2024
↑ https://cdn-reichelt.de/documents/datenblatt/A300/101020018_01.pdf, abgerufen am 14.07.2024

[1] ttps://cdn-reichelt.de/documents/datenblatt/A300/101020018_01.pdf, abgerufen am 14.07.2024

[2] ttps://wiki.hshl.de/wiki/index.php/BSE_Angewandte_Informatik_-_SoSe24, abgerufen am 14.07.2024

[3] ttps://de.mathworks.com/products/simulink.html, abgerufen am 14.07.2024

[4] ttps://docs.arduino.cc/hardware/uno-rev3/, abgerufen am 14.07.2024

[5] ttps://cdn-reichelt.de/documents/datenblatt/A300/101020018_01.pdf, abgerufen am 14.07.2024

[6] ttps://wiki.hshl.de/wiki/index.php/Steckbrett, abgerufen am 14.07.2024

[7] ttps://wiki.hshl.de/wiki/index.php/LCD_Modul_16x02_I2C, abgerufen am 14.07.2024

[8] ttps://wiki.seeedstudio.com/Grove-Water_Sensor/

[9] ttps://www.mouser.com/datasheet/2/744/Seeed_101020018-1217524.pdf, abgerufen am 21.07.2024

[10] ttps://cdn-reichelt.de/documents/datenblatt/A300/101020018_01.pdf, abgerufen am 14.07.2024

[11] ttps://cdn-reichelt.de/documents/datenblatt/A300/101020018_01.pdf, abgerufen am 14.07.2024

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

@@ Zeile 147: / Zeile 147: @@
 == Versuchsaufbau und Durchführung ==
 === Versuchsaufbau ===
-[[Datei:Grove Water Sensor Anschlussplan.png|thumb|right|200px|Abb. 3: Grove Water Sensor Anschlussplan]]
 Der Versuchsaufbau wird durch einen Anschlussplan '''(Abbildung. 3)''' und einem Foto des Aufbaus '''(Abbildung. 4)''' dokumentiert.
 <br>
+[[Datei:Grove Water Sensor Anschlussplan.png|thumb|right|200px|Abb. 3: Grove Water Sensor Anschlussplan]]
+<br clear = all>
 '''Sensor'''<br>
 Der Sensor wird mit dem Arduino über drei Kabel verbunden. Der VCC Anschluss des Sensors wird mit den 5V Versorgungsspannung des Arduinos und GND des Sensors mit GND des Arduinos verbunden. Der Kontakt SIG wird an den analogen Port (A0) angeschlossen.