UV-Sensor UVM30A

Abb. 1: UV-Sensor UVM30A

Autor:	Oliver Scholze
Studiengang:	Business and Systems Engineering
Modul:	BSE-M-2-1.03, Hausarbeit in Angewandte Informatik gehalten von Prof. Dr.-Ing. Schneider
Semester:	Sommersemester 2024
Abgabetermin:	28.07.2024

Einführung

Der Sensor im UVM30A ist ein photodetektiver Sensor, der UV-Licht im Bereich von 200 nm bis 370 nm erfasst. Dieser photodetektiver Sensor besteht aus einem Halbleitermaterial, das bei Bestrahlung mit UV-Licht Elektronen freisetzt. Diese freigesetzten Elektronen erzeugen einen elektrischen Strom, der proportional zur Intensität des einfallenden UV-Lichts ist, diese wird auch als photoelektrischer Effekt bezeichnet. Dieser Strom wird dann in eine analoge Spannung umgewandelt, die vom Sensor ausgegeben wird. Die analoge Ausgangsspannung wird mithilfe des Diagramms, aus dem Datenblatt, in einen UV-Index umgewandelt.

Aufgabenstellung

Messen Sie Intensität eines gegebenen ultravioletten Lichts. Zeigen Sie auf dem Display an, welchem UV Index die Intensität entspricht.

Anforderungen 

Tabelle 1: Anforderungen

Req.	Beschreibung	Priorität
1	Die Intensität des ultravioletten Lichts muss mittels UV-Sensor UVM30A, Arduino und Simulink gemessen werden.	1
2	Der Messbereich muss bestimmt werden.	1
3	Die Messunsicherheit (1σ) muss für den Messbereich ermittelt und als Vertrauensbereich angezeigt werden.	1
4	Der Sensor muss kalibriert werden.	1
5	Für den Messbereich muss die Intensität des ultravioletten Lichts referenziert werden.	1
6	Die Messwerte müssen über der Zeit gefiltert werden.	1
7	Ein Piepton muss anzeigen, wenn der Messwert stabil/konstant ist.	1
8	Das Sensorsystem muss die Intensität und den dazugehörigen UV Index auf dem LCD-Display anzeigen.	2

• Thema/Fragestellung: Messung der UV-Intensität erfolgt mit dem Sensor UVM30A.
• Hypothese: Die Wellenlängen lassen sich im Bereich von 200 nm-370 nm fehlerfrei messen.
• Einordnung in den Lehrplan Für die Aufgabe werden Inhalte aus der Vorlesung Angewandte Informatik und Signalverarbeitende Systeme benötigt, da somit die Implementierung/ Durchführung und die Bewertung des Ergebnisses erfolgen kann.

Projektbeschreibung

Tabelle 2: Materialliste

#	Anzahl	Material
1	1	PC mit MATLAB/Simulink R2023b
2	1	UV-Sensor - UVM30A
3	1	Arduino Uno R3
4	1	Streckbrett
5	5	Jumper Kabel, männlich/männlich, 20 cm
5	1	LCD-Display mit I2C

Beschreibung Funktionsweise der verwendeten Hard- und Software

• Arduino Uno R3: Der Arduino Uno R3 ist das Herzstück des Systems und dient als Mikrocontroller.
• UVM30A: Der Sensor erzeugt ein elektrisches Signal, dessen Spannung von der Intensität der UV-Strahlung abhängt, die auf den Sensor trifft.
• Simulink R2023b: Erstellung des Programms zur Ansteuerung und Auswertung der angeschlossenen Hardware (UVM30A und LCD Display).
• LCD-Display mit I2C: Das LCD-Display wird verwendet, um die gemessenen UV-Intensitätswerte anzuzeigen.
• Steckbrett: Ein Steckbrett dient zum schnellen und flexiblen Aufbau und Testen von elektronischen Schaltungen ohne Löten.
• Jumperkabel: Jumperkabel werden verwendet, um Verbindungen zwischen verschiedenen Komponenten auf einem Steckbrett oder zwischen einem Steckbrett und einem Arduino herzustellen.

Technische Daten

Messbereich	200-370 nm
Versorgungsspannung	3 V .. 5 V
Versorgungsstrom	0.06 mA, maximal 0.1 mA
Genauigkeit	+-1 UV Index
Gewicht	13 g
Getriebe	Kunststtoff
Arbeitstemperatur	-20 °C .. +85 °C
Abmessungen	34 mm x 13 mm x 7 mm

Pinbelegung

Pin	Belegung	Signal
1	Versorgungsspannung VCC	5 V
2	Analoger Ausgang	0 V .. 1.16 V
3	Masse (GND)	0 V

Versuchsaufbau und Durchführung

Versuchsaufbau

Abb. 2: Schaltplan	Abb. 3: Anschlussplan

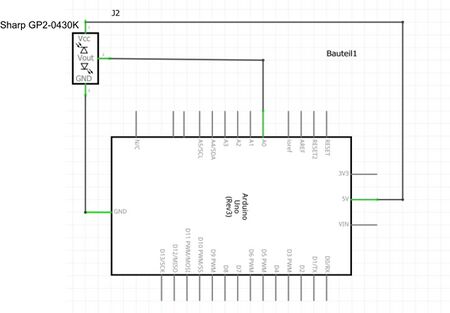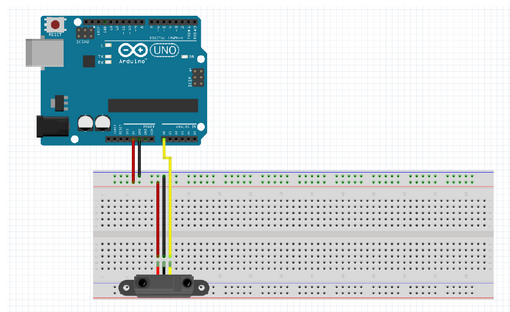Implementierung in Simulink

Umwandlung der Ausgangsspannung in einen UV-Index

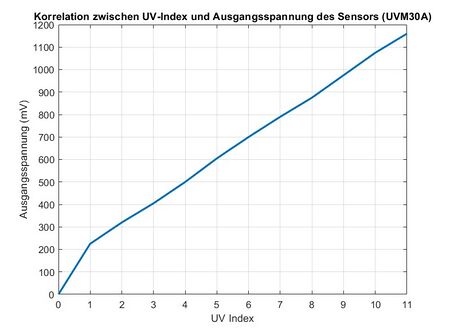
Für die Umwandlung wird eine Kennlinie benötigt, um die Beziehung zwischen der analogen Ausgangsspannung und der UV-Intensität zu beschreiben. Diese Kennlinie wird mithilfe der vom Hersteller gegebenen Daten erstellt und ist notwendig, um die Messwerte korrekt zu interpretieren. Für die Interpretation wird Simulink eine 1D-Lookuptabel verwendet, welche die unten genannten Werte enthält:

Abb. 2: Korrelation zwischen UV-Index und Ausgangsspannung des Sensors

% Werte für den 1-D Lookup-Table zur Umwandlung der Spannungswerte in den UV-Index
Output_Voltage = [0 225 320 405 500 605 700 790 875 975 1075 1160]; % Wert aus AD-Wandler [mV]
UV_Index = [0 1 2 3 4 5 6 7 8 9 10 11]; % UV-Wert

Abb. 4: Foto des Versuchsaufbaus

Der Versuchsaufbau wird durch einen Schaltplan (Abb. 2), Anschlussplan (Abb. 3) und Foto des Aufbaus (Abb. 4) dokumentiert.
Verwendete Toolbox: DSP System Toolbox, Simulink Support Package für Arduino Hardware

Versuchsdurchführung

Referenzwert

Als Referenz werden Wetterdaten verwendet aus der die UV-Intensität hervorgeht, um die Kalibrierung des UVM30A durchzuführen. Diese Daten sind präzise und werden regelmäßig gewartet und überprüft, um die Genauigkeit zu gewährleisten.

Abb. 5: Simulink-Modell

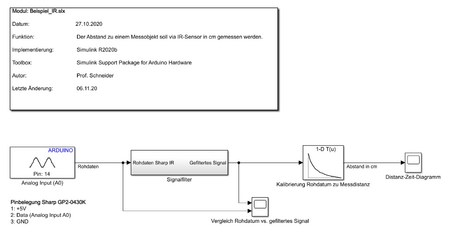
Das Modell zur Datenverarbeitung wurde gemäß Abb. 5 in Simulink aufgebaut. Die Messdaten wurden aufgezeichnet. Ein Video der Versuchsdurchführung findet sich hier.

Modelleinstellungen: Arduino Uno, Solver: Fixed-step, discrete, Abtastrate: 0,001 s

Messprozess und Messunsicherheit

Standardunsicherheit Typ B

Der verwendete Arduino UNO R3 hat einen 10-Bit ADU und eine Referenzspannung von 5V. Daraus ergibt sich eine Quantisierungsstufe von:

$\Delta V = \frac{V_{ref}}{2^{10}} = \frac{5V}{1024} = 4.88mV$

Der maximale Quantisierungsfehler beträgt somit:

$Quantisierungsfehler = \frac{\Delta V}{2} = \frac{4.88mV}{1024} = 4.88mV$

Um den tatsächlichen Fehler berechnen zu können, muss die Standardunsicherheit Typ B des Sensors mithilfe von MATLAB ermittelt werden. Dabei wird geprüft, wie viel Spannung der Messunsicherheit eines UV-Index entspricht. Aus der Kennlinie geht hervor, dass die Umwandlung nahezu linear ist, jedoch nicht vollständig den Anforderungen entspricht. Daher wird zunächst die Differenz zwischen den Spannungswerten berechnet und der Mittelwert dieser Differenzen als Grundlage für die Messunsicherheit verwendet.

Hier ist der MATLAB-Code für die Berechnung des Mittelwerts:

% Gegebene Spannungswerte in mV für die jeden UV-Index von 0 bis 11 von dem Sensor UVM30A
output_voltage = [0, 225, 320, 405, 500, 605, 700, 790, 875, 975, 1075, 1160]; % Wert aus AD-Wandler [mV]

% Differenzen berechnen
differences = diff(output_voltage);

% Mittelwert der Differenzen berechnen
mean_difference = mean(differences);

% Mittelwert ausgeben
disp('Der Mittelwert der Differenzen ist:');
disp(mean_difference);

Dadurch ergibt sich eine kombinierte Standardunsicherheit von:

$Standardunsicherheit TYP B = \sqrt{Messunsicherheit^2+Quantisierungsfehler^2} = \sqrt{(105.45mV)^2+(4.88mV)^2} = 105.56mV$

Der tatsächliche Fehler dieser Messung unter Berücksichtigung der Messunsicherheit des UV-Sensors und des Quantisierungsfehlers des 10-Bit AD-Wandlers beträgt etwa 105.56 mV.

====Standardunsicherheit TYP A und C====
Zuletzt erfolgt die Berechnung der kombinierten Standardunsicherheit Typ C die anhand einer Messung erfolgt und hier erläutert wird:

Hier ist der Matlab-Code:

%****************************************************************
%                   Hochschule Hamm-Lippstadt                   *
%****************************************************************
% Modul	          : BerechnungderStandardunsicherheit.m         *
%                                                               *
% Datum           : 15.07.2024                                  *
%                                                               *
% Funktion        : Berechnung der Standarunsicherheiten und    *
%                   der Abweichungen vom Messergebnis           *
%                                                               *
% Implementation  : MATLAB 2023b                                *
%                                                               *
% Req. Toolbox    : Statistics and Machine Learning Toolbox     *
%                                                               *
% Author          : Oliver Scholze                              *
%                                                               *
% Bemerkung       :   -                                         *
%                                                               *
% Letzte Änderung : 15.07.2024                                  *
%                                                               *
%% Messdaten laden 
load('Vertrauensbereich.mat');
data = gefiltertes_Signal.data; % Annahme: gefiltertes_Signal.data ist die 3D-Matrix mit den Messwerten

% Messwerte in mV (falls nötig, hier anpassen)
Rm = gefiltertes_Signal.data(1,1,:); 

% Anzahl der Messwerte bestimmen
n = numel(Rm);  % Anzahl der Messungen

%% Bester Schätzwert des Widerstandes berechnen
R = mean(Rm(:));  % Mittelwert der Messwerte

%% Empirische Standardabweichung bestimmen
s = std(Rm(:));

%% Standardunsicherheit Typ A bestimmen
p = normcdf(R+s, R, s) - normcdf(R-s, R, s); % Vertrauensniveau
nu = n - 1; % Freiheitsgrade

%% t-Quantil berechnen
t = tinv((1+p)/2, nu);
disp(['t-Faktor: t = ', num2str(t)]);

%% Unsicherheit Typ A
uA = s * t / sqrt(n);

%% Standardunsicherheit Typ B bestimmen (angenommen)
uB = 105.56;  % Angenommener Wert für Unsicherheit Typ B

%% Kombinierte Standardunsicherheit Typ C bestimmen
uC = sqrt(uA^2 + uB^2); % Unsicherheit Typ C

%% Grad des Vertrauens bestimmen
k = 2;  % Vertrauensfaktor

%% Absolute Messunsicherheit bestimmen
uAbs = k * uC; % Absolute Messunsicherheit

%% Relative Messunsicherheit berechnen (%)
uRel = (uAbs / R) * 100;

%% Ergebnisdarstellung
figure;
yline(R, 'Color', 'k');
xlim([0 3200])
hold on;
plot([0 n], [R+uC R+uC], '--b', [0 n], [R-uC R-uC], '--b');
plot(1:n, reshape(Rm, 1, []));  % Um die Daten zu plotten, in einen Vektor umformen

% Beschriftungen hinzufügen
xlabel('Anzahl der Messwerte');
ylabel('Ausgangsspannung in mV');
title(['Messergebnis (Mittelwert = ', num2str(R), ', Unsicherheit = \pm', num2str(uC), ' mV)']);

% Legende erstellen
legend({'Mittelwert', 'Unsicherheit Typ C'}, 'Location', 'northwest');

Versuchsbeobachtung

Abb. 6: Darstellung des Rohsignals des IR-Entfernungssensors (rote Kurve)	Abb. 7: Darstellung von dynamischen Messwerten des IR-Entfernungssensors

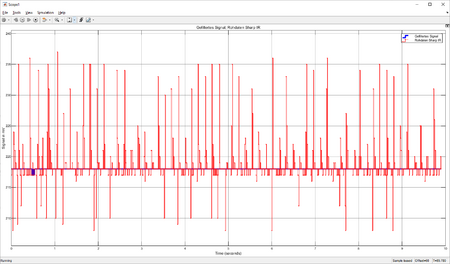
Das Signal des Sensors weist alle 40 ms systematische Ausreisser auf (vgl. Abb. 6, rote Kurve).

Auswertung

Die Messhypothese wurde verworfen. Der Sensor weist systematische Messwertausreisser auf.

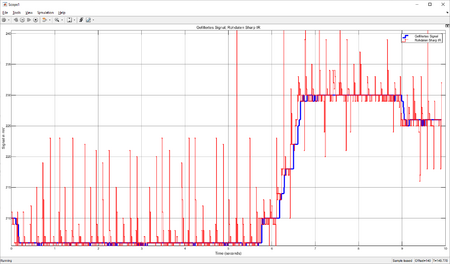
Die Ausreisser lassen sich mit einem Signalfilter eliminieren. Hierzu eignet sich ein Rangordnungsfilter (z. B. Median-Filter). Das Filter wird hierzu auf eine Fensterbreite von 30 Werten eingestellt. Das zufriedenstellende Filterergebnis für statische Werte zeigt Abb. 6 als blaue Kurve. Es konnte mit dynamische Werten verifiziert werden (vgl. Abb. 7). Das Datenblatt ([2, S. 6]) belegt die Messungen und bezeichnet die Messausreisser als "instabile Ausgabe" für maximal 5 ms alle 40 ms. Mit 50 Werten erhöht sich die Filterwirkung, es entsteht jedoch ein Delay von 10 ms. Mit 10 Werten ist die Filterwirkung zu gering.

Zusammenfassung und Ausblick

• Zusammenfassung der Kapitel 1-4
• Diskussion der Ergebnisse
• Ausblick
• Selbstreflexion/Lessons learned

Ergebnisvideo

Binden Sie hier Ihr Ergebnisvideo ein.

Anleitung: Videos im Wiki einbinden

Lernzielkrontrolle

Beantworten Sie in Ihrem Artikel die Lernzielkontrollfragen.

Lernzielkontrollfragen 

1. Wie funktioniert der Primärsensor technisch?
2. Welche Leistungsmerkmale hat der Sensor?
3. Wie funktioniert die Umsetzerschaltung technisch?
4. Wie kommuniziert der Sensor mit dem Arduino?
5. Muss der Sensor kalibriert werden?
6. Wie wird der Messwert in die zu messende physikalische Größe umgerechnet?
7. Was nutzen Sie als Referenz?
8. Benötigt der Sensor eine Kennlinie?
9. Welchen Messbereich hat das Signal am Ende der Messkette?
10. Welche Messunsicherheit und welcher Vertrauensbereich hat das Signal am Ende der Messkette für den gesamten Messbereich?
11. Welche Auflösung hat das Signal am Ende der Messkette? Wodurch wird die Auflösung bedingt?
12. Weist das Signal am Ende der Messkette einen systematischen oder zufälligen Fehler auf?
13. Welche Fehlereinflüsse hat die Messung? Muss z. B. die Temperatur der Messung berücksichtigt werden?

Literatur

Zitieren Sie nach DIN ISO 690:2013-10. https://www.wiltronics.com.au/wp-content/uploads/datasheets/ARD2-2062.pdf

Anhang

• Datenblätter
• Simulink-Modell
• Originaldateien (PAP, Schaltplan,... )

---

→ zurück zum Hauptartikel: BSE Angewandte Informatik SoSe24 | Hausarbeit SoSe24