Herzfrequenz/Pulsesensor SE050

Abb. 1: Herzfrequenz/Pulsesensor SE050

Autor:	Weiran Wang
Studiengang:	Business and Systems Engineering
Modul:	BSE-M-2-1.03, Hausarbeit in Angewandte Informatik gehalten von Prof. Dr.-Ing. Schneider
Semester:	Sommersemester 2024
Abgabetermin:	28.07.2024

Einführung

Aufgabenstellung

Messen Sie die die Herzfrequenz am Ohrläppchen oder Finger in Herzschlag pro Minute (BPM).

Anforderungen 

Tabelle 1: Anforderungen

Req.	Beschreibung	Priorität
1	Die Herzfrequenz muss mittels Pulsesensor SE050, Arduino und Simulink gemessen werden.	1
2	Der Messbereich muss bestimmt werden.	1
3	Die Messunsicherheit (1σ) muss für den Messbereich ermittelt und als Vertrauensbereich angezeigt werden.	1
4	Der Sensor muss kalibriert werden.	1
5	Für den Messbereich muss die Pulsfrequenz referenziert werden.	1
6	Die Messwerte müssen über der Zeit gefiltert werden.	1
7	Ein Piepton muss anzeigen, wandelt den Herzschlag in ein akustisches Signal um.	1
8	Das Sensorsystem muss die Herzschläge pro Minute auf dem LCD-Display anzeigen.	2

• Thema/Fragestellung: Messung der Herzfrequenz mit dem Pulsesensor SE050
• Hypothese: Herzfrequenz kann fehlerfrei gemessen werden.
• Einordnung in den Lehrplan

Projektbeschreibung

Tabelle 2: Materialliste

#	Anzahl	Material
1	1	PC mit MATLAB/Simulink R2023b
2	1	Pulsesensor SE050
3	1	Arduino Uno R3
4	1	Streckbrett
5	?	Jumper Kabel, männlich/männlich, 20 cm

Beschreibung Funktionsweise der verwendeten Hard- und Software

• Arduino Uno R3

Arduino Uno R3 ist ein Open-Source-Mikrocontroller-Entwicklungsboard, das von der Firma Arduino entwickelt und produziert wurde. Es integriert viele wichtige Komponenten. Zu den Hauptkomponenten gehören der Atmega328P-Mikrocontroller, eine externe Quarzquelle zur Bereitstellung einer hohen Taktfrequenz, ein Upload-Gerät, das aus einer USB-Schnittstelle und einem Atmega16U2-Signalumwandlungsmodul besteht, eine Reset-Taste zum Neustarten von Programmen sowie zwei Reihen von Schnittstellen zur Verbindung von Peripheriegeräten. Da ein Mikrocontroller der AVR-Serie verwendet wird, unterstützt das Arduino-Board eine Vielzahl von Funktionen wie digitale Ein-/Ausgabe, analoge Ein-/Ausgabe, Timer/Zähler und Interrupts, die die grundlegenden Anforderungen eingebetteter Systeme erfüllen.

• Pulsesensor SE050

Pulse Sensor ist ein Open-Source-Hardwareprojekt, das von Joel Murphy und Yury Gitman entwickelt wurde. Aus den verfügbaren Informationen und durch direkte Beobachtung lässt sich erkennen, dass der Pulse Sensor eine runde Leiterplatte (PCB) ist, die verschiedene Komponenten integriert. Zu den wichtigsten Komponenten gehören der Lichtsensor „APDS-9008“ und eine grüne LED von „Kingbright“. Diese beiden Komponenten ermöglichen die Photoplethysmographie (PPG)-Technologie. Genauer gesagt, sendet die grüne LED Licht auf die Haut, wobei ein Teil des Lichts vom Blut absorbiert und ein Teil vom Gewebe reflektiert wird und auf den „APDS-9008“-Lichtsensor trifft. Durch die Erkennung der durch den Blutfluss verursachten Änderungen dieser Lichtstrahlen kann die Herzfrequenz gemessen werden.

• LCD Modul 16x02 I2C

• Simulink R2023b

Um die Analyse von Sensordaten zu erleichtern, werden Matlab & Simulink verwendet. Darüber hinaus muss zur Unterstützung von Arduino-Projekten das Plugin „Simulink Support Package for Arduino Hardware“ heruntergeladen und installiert werden. Durch die Verwendung des Simulink Support Package for Arduino Hardware können Entwickler effektiv RCP (Rapid Control Prototyping) durchführen, wodurch der Entwurfs- und Validierungsprozess von Steuerungssystemen beschleunigt wird. Konkret ermöglicht der Einsatz dieses Plugins, dass Modelle, die auf Arduino-Funktionen basieren, in Maschinencode umgewandelt und auf die Arduino-Entwicklungsplatine hochgeladen werden. Anschließend können die Ausgaberesultate der Arduino-Entwicklungsplatine in Echtzeit in Simulink beobachtet werden.

Technische Daten

Messbereich	unbekannt
Versorgungsspannung	3.3 V oder 5.0 V
Versorgungsstrom	< 4 mA
Ausgangssignaltyp	Analogsignal
Ausgangssignalbereich	0.3 V .. VCC V
Getriebe	Kunststtoff
Arbeitstemperatur	-40 °C .. +85 °C
Abmessungen	∅ = 15.8 mm ; δ = 3.6 mm

Pinbelegung

Pin	Belegung	Signal
1	Signal	Analogsignal (0.3 V .. 5 V)
2	Versorgungsspannung VCC	5 V
3	Masse (GND)	0 V

Versuchsaufbau und Durchführung

Versuchsaufbau

Abb. 2: Schatplan

Abb. 3: Anschlussplan

Abb. 4: Versuchsaufbau

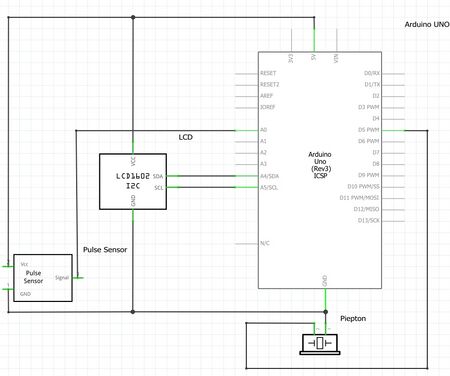
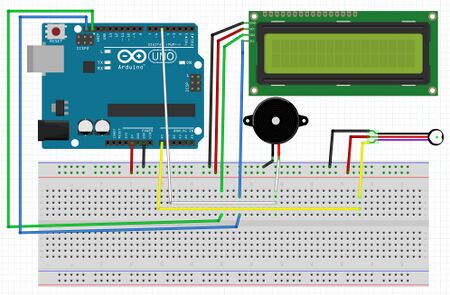
Der Versuchsaufbau wird durch einen Schaltplan (Abb. 2), Anschlussplan (Abb. 3) und Foto des Aufbaus (Abb. 4) dokumentiert.

Versuchsdurchführung

Abb. 5: Externe Lichtquellen isolierender Pulse Sensor

Abb. 6: Messdaten des Stillstands

Abb.7 : Darstellung der Messunsicherheit

Abb. 8: Simulink-Modell

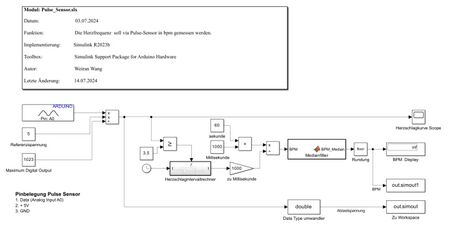
• Erste Modellierung

Pulse Sensor verwendet die PPG-Technologie. Während des Betriebs des Geräts wird das Pulssignal synchron und kontinuierlich mit den Pulsschwingungen ausgegeben. Daher reicht es aus, den Zeitraum dieses Schwingungssignals zu bestimmen, um die momentane Herzfrequenz zu ermitteln.

Beim Erstellen des Modells muss das Analog Input-Block verwendet werden, um die Ausgangsabtastung des Pulse Sensors vom Arduino UNO R3 zu erhalten und in ein Digitalsignal umzuwandeln.

Aus dem Datenblatt des Mikrocontrollers Atmega328P geht hervor, dass die ADC-Umwandlungszeit maximal 260 µs beträgt, während das Abtastintervall 67 µs beträgt. Daher beträgt die gesamte A/D-Umwandlungszeit 327 µs und ist somit kleiner als 1 ms. Daher kann die Systemabtastuhr in Simulink mit discretem Fixed-step auf 0,001 s fest eingestellt werden.

Beobachtungen zeigen, dass bei jedem Herzschlag ein höherer und ein niedrigerer Peak im Signal auftreten. Der höhere Peak repräsentiert den Herzschlag, während der niedrigere Peak aufgrund der Struktur der Blutgefäße entsteht. In diesem Projekt kann der niedrigere Peak ignoriert werden. Daher kann ein Filter, der aus einem Constant-Block und einem Relational Operator-Block besteht, verwendet werden, um die höheren Peaks zu erhalten. Der Wert des Constant-Blockes wird auf 3,5 gesetzt. Es reicht aus, das Zeitintervall der ansteigenden Flanke des Signals, das den Schwellenwert von "3,5" überschreitet, zu erkennen und die Umrechnungsformel zu verwenden, um die momentane Herzfrequenz zu berechnen.

Da das Herzfrequenzmessgerät, bestehend aus dem Pulse Sensor und dem Arduino UNO R3, während des Signalwandlungsprozesses einige Fehler verursachen kann, ist es notwendig, die Messfehler des Geräts zu bestimmen und zu analysieren, ob diese Fehler die Herzfrequenzmessung negativ beeinflussen können.

• Vorläufige Bewertung der Messunsicherheit

Da die Herzfrequenz eine nicht kontrollierbare Variable ist, kann im Messdesign kein bestimmter Wert als Referenzstandard festgelegt werden. Daher kann das Messgerät nur vor der Herzfrequenzmessung, wenn die Herzfrequenz null ist, kalibriert werden. Externe Lichtquellen isolierender Pulse Sensor(Abb. 3) zeigt den auf dem Tisch ruhenden Pulse Sensor, der von externen Lichtquellen abgeschirmt ist. Die Erfassung der Ausgangsspannung des Pulse Sensors in diesem Zustand sollte im Laufe der Zeit einen relativ stabilen Wert nahe VCC/2 zeigen.

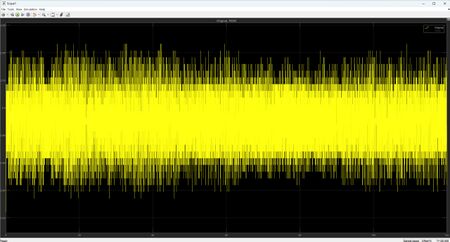
Messdaten des Stillstands (Abb. 4) zeigen die Daten innerhalb von zwei Minuten. Die Messwerte schwanken zwischen 2,44 V und 2,54 V, ohne große Abweichungen. Diese Schwankungen können durch externe elektromagnetische Störungen, sensorinterne Geräusche und ADC-Quantisierungsrauschen verursacht werden. Daher können die im Diagramm dargestellten zufälligen Fehler als Standardunsicherheit Typ A kategorisiert werden.

• Die konkrete Messunsicherheit mit Matlab berechnen

Die Verwendung von Matlab ermöglicht eine einfache Bestimmung der Messunsicherheit. Zunächst werden die gemessenen Spannungsdaten aus Simulink in den Workspace importiert, um die Standardunsicherheit Typ A durch die Anwendung statistischer Methoden zu bestimmen. Anschließend werden die Spezifikationsparameter der Hardwaregeräte, wie z.B. Kalibrierzertifikate und technische Spezifikationen des Herstellers, gesammelt, um die Standardunsicherheit Typ B zu bestimmen. Schließlich werden die Standardunsicherheiten der Typen A und B zur Typ-C-Standardunsicherheit kombiniert.

Im folgenden Fenster zeigt sich ein MATLAB-Algorithmus, der zur Berechnung des wahren Werts der gemessenen Spannung innerhalb 2 Minuten, der Standardunsicherheit sowie der absoluten Messunsicherheit innerhalb von ±1σ einer Gaußschen Verteilung dient. In dem Algorithmus wurde bei der Bestimmung der Standardunsicherheit TypB aufgrund fehlender detaillierter Informationen über den Pulse Sensor nur die Herstellerdaten des ADC-Wandlers des Arduino UNO R3 verwendet.Beim Durchsehen des Datenblatts des Atmega328p können die folgenden Eigenschaften seines ADC-Komponenten festgestellt werden: Der maximale Wert der absoluten Genauigkeit beträgt 3,5 LSB, der maximale Wert der Integral-Nonlinearität beträgt 1,5 LSB, der maximale Wert der Differenzial-Nonlinearität beträgt 0,7 LSB, der Bereich des Verstärkungsfehlers beträgt 3,5 LSB und der Bereich des Offset-Fehlers beträgt 3,5 LSB. Bei der Berechnung der Standardunsicherheit vom Typ B wird angenommen, dass diese Fehler gleichmäßig verteilt sind, und ihre Standardunsicherheit wird als diese Maximalwerte geteilt durch √3berechnet.

%% Daten aus dem Workspace abrufen
Daten = simout;    

%% Datenverarbeitung
n = length(Daten);             % Die Anzahl der Daten ermitteln
RE = mean(Daten);                   % Den Durchschnitt berechnen
sE = std(Daten);               % Die Standardabweichung berechnen

%% Die Paramete aus Atmega328p-Datenblatt
Aufloesung = 10;                            % Aufloesung，10 bit
v_ref = 5;                      % Referenz Spannung, Einheit : V
lsb = v_ref / (2^Aufloesung);   % Mindestaufloesung，Einheit: V

% Jede Fehlerquelle （Einheit：LSB）
absolute_genauigkeit_lsb = 3.5;  % Absolute Genauigkeit, maximal
inl_lsb = 1.5;        % Integraler nichtlinearer Fehler, Maximum
dnl_lsb = 0.7;  % Differenzieller Nichtlinearitätsfehler, maximal
gain_error_lsb = 3.5;              % Verstärkungsfehler, maximal
offset_error_lsb = 3.5;                       % Offsetfehler, max.

%% Fehlerquelle in Spannung umrechnen (Einheit: V)
absolute_genauigkeit = absolute_genauigkeit_lsb * lsb; 
inl_error = inl_lsb * lsb;
dnl_error = dnl_lsb * lsb;
gain_error = gain_error_lsb * lsb;
offset_error = offset_error_lsb * lsb;

%% Berechnen Standardunsicherheit Typ A
alpha = 1-0.6827;
p = 1-(alpha/2);
t = tinv(p,n-1); 
uA = t*sE/sqrt(n); 

%% Berechnen die Standardunsicherheit Typ B
uB = sqrt(absolute_genauigkeit^2 + inl_error^2 + dnl_error^2 + gain_error^2 + offset_error^2 );

%% Berechnen Standardunsicherheit Typ C
uC = sqrt((uA)^2+(uB)^2);  

%% Berechnen absolute Messunsicherheit 
k  = 2; % Vertrauensfaktor (Vertrauensniveau 0.9545)
uAbs = k*uC; % absolute Messunsicherheit 

%% Vollständige Messergebnis
disp(['Vollständige Messergebnis: U = ',num2str(RE),' ± ',num2str(uAbs),' V '])

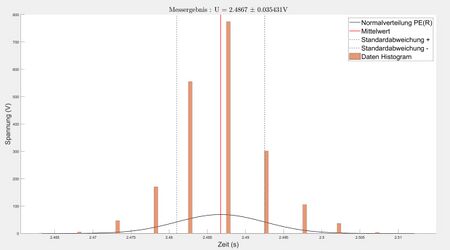
Durch die Anwendung des oben genannten Matlab-Algorithmus ergibt sich ein vollständiges Messergebnis: U = 2,4867 ± 0,035431 V. Dabei repräsentiert "2,487" den Mittelwert, also den wahren Wert, und "0,035" die absolute Messunsicherheit.

• Darstellung der Messunsicherheit(1σ)

Der folgende Matlab-Code dient zur Visualisierung der oben berechneten Daten. Mit diesem Code kann die Verteilung der gemessenen Spannung dargestellt werden, einschließlich der Wahrscheinlichkeitsdichtekurve der Spannungsdaten, des Durchschnittswertes der Spannungsdaten, der Position einer Standardabweichung sowie des Histogramms der Spannungsdaten . Der Titel gibt den Durchschnittswert und die Unsicherheit des kompletten Messergebnisses an. Das Ergebnis der Programmausführung ist in der Darstellung der Messunsicherheit(Abb.7)zu sehen.

Max = max(Daten);  %% Den Maximalwert im Daten-Array finden
Min = min(Daten);  %% Den Minimalwert im Daten-Array finden
x = Min:0.0001:Max;%% Einen Bereich vom Minimalwert bis zum Maximalwert erstellen
pE = normpdf(x,RE,sE ); 

figure;
hold on;

% Zeichnen der Wahrscheinlichkeitsdichtekurve
p1 = plot(x, pE, 'LineWidth', 1, 'Color', 'black', 'DisplayName', 'Normalverteilung PE(R)');

% Zeichnen des echten Werts mit roter Farbe
p2 = xline(RE, 'Color', 'red', 'LineWidth', 2, 'DisplayName', 'Mittelwert');

% Markieren der Standardabweichung
p3 = xline(RE + sE, 'k--', 'LineWidth', 1, 'DisplayName', 'Standardabweichung +');
p4 = xline(RE - sE, 'k--', 'LineWidth', 1, 'DisplayName', 'Standardabweichung -');

% Zeichnen der Anzahlen der verschiedenen Spannungen
p5 = histogram(Daten, 'Normalization', 'pdf', 'DisplayName', 'Daten Histogram');

% Legend hinzufügen
lgd = legend([p1 p2 p3 p4 p5]);
lgd.FontSize = 18;  % Hier die gewünschte Schriftgröße einstellen
xlabel('Zeit (s)', 'FontSize', 18);
ylabel('Spannung (V)', 'FontSize', 18);
title({['Messergebnis : U = ', num2str(RE), ' $\pm$ ', num2str(uAbs), 'V']}, ...
'Interpreter', 'latex', 'FontSize', 18);
hold off;

• Kalibrierung

Der gemessene Spannungswert weist sehr wahrscheinlich einen systematischen Fehler auf. Dieser systematische Fehler hat jedoch keinen Einfluss auf die Messung der Herzfrequenz, da dieser Fehler lediglich zu einer Gesamtverschiebung der Spannungsdaten führt. Die Genauigkeit der Herzfrequenzberechnung hängt von der Präzision der Zeitabstände zwischen den definierten Anstiegsflanken der Herzfrequenzwellenform ab. Daher muss der systematische Fehler nicht korrigiert werden.

• Nachteilige Auswirkungen der Messunsicherheit

Durch Experimente und Analysen wurde festgestellt, dass die Messunsicherheit zwischen -0,035 und +0,035 V liegt. Diese Messunsicherheit kann dazu führen, dass der aktuell gemessene Spannungswert das Modul zur Berechnung der Herzschlagzeitintervalle (bei der ansteigenden Flanke der Herzschlagwelle und einem Messwert größer als der eingestellte Schwellenwert von 3,5 V) vorzeitig oder verspätet auslöst, wodurch die Genauigkeit der Herzfrequenzmessung indirekt beeinflusst wird.

Zum Beispiel: Angenommen, der aktuell gemessene Spannungswert beträgt 3,465 V, was unterhalb des Auslöseschwellenwerts liegt. Aufgrund der Messunsicherheit könnte dieser Spannungswert jedoch auf 3,465 V + 0,035 V erhöht werden, was zu einer vorzeitigen Auslösung führt.

Ebenso könnte der gemessene Spannungswert, wenn er genau 3,5 V beträgt und somit die Auslösebedingungen erfüllt, aufgrund der Messunsicherheit unter 3,5 V fallen, wodurch das Modul zur Berechnung der Herzschlagzeitintervalle nicht ausgelöst wird, was zu einer verspäteten Auslösung führt.

Offensichtlich führen vorzeitige oder verspätete Auslösungen zu Fehlern bei den Herzschlagzeitintervallen. Daher muss analysiert werden, ob diese vorzeitigen oder verspäteten Auslösungen durch Filter eliminiert werden können. Falls dies nicht möglich ist, sollte bewertet werden, wie groß die durch vorzeitige oder verspätete Auslösungen verursachten Zeitfehler sind.

Darüber hinaus könnte die ungenaue Auslösung dazu führen, dass das Modul innerhalb einer sehr kurzen Zeitspanne mehrmals ausgelöst wird, wodurch die angezeigte Herzfrequenz unzuverlässig wird.

Zum Beispiel: Angenommen, der gemessene Spannungswert beträgt 3,465 V und wird aufgrund der Messunsicherheit auf 3,5 V erhöht, wodurch das Modul ausgelöst wird. Theoretisch sollte der nächste Auslösezeitpunkt des Moduls bei der nächsten ansteigenden Flanke des Herzschlags liegen. Aufgrund der sehr kurzen Simulink-Abtastzeit könnte der Spannungswert jedoch im nächsten Abtastschritt der ansteigenden Flanke des aktuellen Herzschlags nicht signifikant ansteigen und aufgrund der Messunsicherheit auf unter 3,5 V fallen, wodurch er unter den vorherigen Abtastspannungswert fällt und eine abfallende Flanke erzeugt. Nach einigen Abtastschritten wird der Spannungswert jedoch wieder über 3,5 V steigen und die Auslösebedingungen erneut erfüllen, was zu einer kurzen, aufeinanderfolgenden Auslösung des Moduls führt. Daher muss festgestellt werden, ob dieses Risiko besteht, und es müssen Methoden gefunden werden, um dieses Risiko vollständig zu eliminieren.

• Verzicht auf die Verwendung eines Filters dabei

Ein Tiefpassfilter eignet sich zur Filterung der Herzschlag-Abtastspannung, reduziert scharfe Schwankungen und Störungen, verbessert das Signal-Rausch-Verhältnis und glättet das Spannungssignal, sodass das Signal stabiler und kontinuierlicher wird. Obwohl der Tiefpassfilter Hochfrequenzrauschen effektiv unterdrücken kann, kann er das Rauschen nicht vollständig beseitigen, sodass das Problem der ungenauen Auslösung nicht behoben wird. Daher kann auf die Verwendung des Filters verzichtet werden.

• Risikobeseitigung

Im oben genannten Text wurde erwähnt, dass das Risiko besteht, dass das Modul zur Berechnung der Herzschlagzeitintervalle innerhalb eines sehr kurzen Zeitraums mehrfach ausgelöst wird. Um dieses Risiko zu beseitigen, muss sichergestellt werden, dass die Spannung im nächsten Abtastschritt nach der Auslösung nicht mehr unter den festgelegten Auslöseschwellenwert (3,5 V) fällt.

Beobachtungen der Herzschlagwelle zeigen, dass die ansteigende Flanke der Welle nahezu linear verläuft und eine hohe Steigrate aufweist. Daher reicht es aus, das Abtastzeitintervall zu verlängern, um sicherzustellen, dass die Spannung einen ausreichenden Anstieg aufweist. Wenn der Spannungsanstieg größer ist als der maximale Unterschied der Messunsicherheit benachbarter Abtastwerte, d. h. das Doppelte der Messunsicherheit, kann sichergestellt werden, dass die Spannung beim nächsten Abtastschritt definitiv über 3,5 V liegt, wodurch das Risiko einer mehrfachen Auslösung beseitigt wird.

Um die Spannungszunahme bei unterschiedlichen Abtastintervallen zu berechnen, müssen zunächst die Abtastpunkte entlang der ansteigenden Flanke durch lineare Regression angepasst werden, um eine Funktion zu erhalten. Anschließend kann durch Einsetzen verschiedener Zeitintervalle die Spannungszunahme ermittelt werden.

Die folgende MATLAB-Funktion extrahiert die Spannungsdaten entlang der ansteigenden Flanke und führt eine lineare Regression dieser Datenpunkte durch, basierend auf dem aktuellen Modell mit einer Abtastzeit von 1 ms.

% Extrahieren der Spannungsdaten von der ansteigenden Flanke aus simout
Daten = simout(45:60,1);
% Länge der Daten ermitteln
n = length(Daten);
% Erstellen der Zeitdaten von 1 bis n
Zeit = 1:n;

% Definieren von x als Zeit und y als Daten
x = Zeit;
y = Daten;

% Berechnung der Kovarianzmatrix von x und y
Kovarianzmatrix = cov(x, y);
% Extrahieren von sxx, syy und sxy aus der Kovarianzmatrix
sxx = Kovarianzmatrix(1,1);
syy = Kovarianzmatrix(2,2);
sxy = Kovarianzmatrix(1,2);

% Berechnung der Regressionskoeffizienten b1 und b0
b1 = sxy/sxx;

% Regressionsgerade berechnen
% Einstellen des Zeitinkrements in Millisekunden
Delta_Zeit = 1; % in ms
% Berechnung des Spannungsinkrements in Volt
Delta_U = b1 * Delta_Zeit % in V

Die Ausführung des obigen Programms ergibt ΔU = 0,065. Dies zeigt, dass das Spannungsinkrement bei einem Abtastzeitintervall von 1 ms kleiner als das Doppelte der Messunsicherheit ist, was bedeutet, dass das Risiko mehrfacher Auslösungen tatsächlich besteht. Daher sollte das Simulink-Abtastzeitintervall neu eingestellt werden. Um das Risiko vollständig zu eliminieren, sollte das Abtastzeitintervall auf 3 ms bzw. 0,003 s festgelegt werden.

• Einfluss des Abtastzeitintervalls auf die BPM-Genauigkeit

Da das Modul zur Berechnung der Herzschlagintervalle vorzeitig oder verspätet ausgelöst wird, beträgt der maximale Fehler zwischen dem tatsächlich gemessenen und dem idealen Intervallzeitpunkt: Δ t = 2*3 = 6 ms.

Durch das Hinzufügen dieses Zeitfehlers zur Zeitdauer und das Einsetzen in die Herzfrequenzberechnungsformel kann festgestellt werden, dass die Herzfrequenz dadurch geringfügig schwankt. Da Herzschläge diskret und positive Ganzzahlen sind, muss das Berechnungsergebnis gerundet werden. Bei der Rundung wird in der Regel das mathematische Verfahren „kaufmännisch Runden“ angewendet. Durch den Zeitfehler kann jedoch beim Rundungsverfahren statt aufrunden abgerundet werden und umgekehrt. Daher führt der Spannungsabnahmefehler des Messsystems letztendlich zu einer Herzfrequenzmessunsicherheit von ± 1 BPM.

Herzfrequenzberechnungsformel: $BPM= \frac{60 \cdot 1000}{Zeitdauer}$

• Endmodell

Modelleinstellungen: Arduino Uno, Solver: Fixed-step, discrete, Abtastrate: 0,003 s

Das Modell zur Datenverarbeitung wurde gemäß Abb. 8 in Simulink aufgebaut. Die Messdaten wurden aufgezeichnet. Ein Video der Versuchsdurchführung findet sich hier.

Versuchsbeobachtung

Abb. 9: Darstellung der rohren BPM-Änderungskurve

Abb. 10: Darstellung der Herzschlagkurve

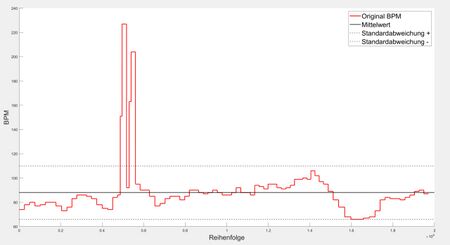
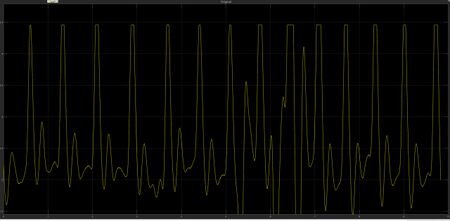
Aus der Darstellung der rohren BPM-Änderungskurve kann man erkennen, dass die Herzfrequenz nicht konstant ist und starke Schwankungen aufweist. Diese Schwankungen sind jedoch nicht durch Messfehler verursacht. Tatsächlich wird die Herzfrequenz von verschiedenen Faktoren beeinflusst, darunter körperliche Aktivität, emotionaler Zustand, Atemmuster, Umweltveränderungen und physiologische Schwankungen im Körper, wie die Regulierung durch das autonome Nervensystem, was zu natürlichen Schwankungen in kurzer Zeit führt.

Um eine repräsentativere Herzfrequenzanzeige zu erhalten, sollten die gemessenen Daten verarbeitet werden, indem mehrere aufeinanderfolgende Messungen durchgeführt und deren Mittelwert bestimmt wird, um zufällige Messfehler zu minimieren. Aus der Darstellung der rohren BPM-Änderungskurve kann man auch einige Extremwerte erkennen. Diese sind auf die Bewegung des Fingers während der Messung zurückzuführen, was zu Veränderungen im Kontakt zwischen dem Pulssensor und der Fingeroberfläche führt (siehe Abb. 10 für die anomale Veränderung der Herzschlagwellenform), was zu anomalen Lichtreflexionen und fehlerhaften Berechnungen der Herzschlagintervalle führt und schließlich zu Extremwerten.

Um diese beiden Probleme zu lösen, wird der rekursive Medianfilter verwendet, da der Medianfilter die zentrale Position einer Gruppe von Messdaten bewerten und die Auswirkungen von Extremwerten verhindern kann. Darüber hinaus ermöglicht der rekursive Medianfilter durch das gleitende Fenster, vergangene Daten zu speichern und sofort die neuesten Messdaten aufzunehmen und zu verarbeiten, was die Echtzeitmessung der Herzfrequenz in gewissem Maße gewährleistet.

Auswertung

Die Messhypothese wurde verworfen. Der Sensor weist systematische Messwertausreisser auf.

Die Ausreisser lassen sich mit einem Signalfilter eliminieren. Hierzu eignet sich ein Rangordnungsfilter (z. B. Median-Filter). Das Filter wird hierzu auf eine Fensterbreite von 30 Werten eingestellt. Das zufriedenstellende Filterergebnis für statische Werte zeigt Abb. 6 als blaue Kurve. Es konnte mit dynamische Werten verifiziert werden (vgl. Abb. 7). Das Datenblatt ([2, S. 6]) belegt die Messungen und bezeichnet die Messausreisser als "instabile Ausgabe" für maximal 5 ms alle 40 ms. Mit 50 Werten erhöht sich die Filterwirkung, es entsteht jedoch ein Delay von 10 ms. Mit 10 Werten ist die Filterwirkung zu gering.

Zusammenfassung und Ausblick

• Zusammenfassung der Kapitel 1-4
• Diskussion der Ergebnisse
• Ausblick
• Selbstreflexion/Lessons learned

Ergebnisvideo

Binden Sie hier Ihr Ergebnisvideo ein.

Anleitung: Videos im Wiki einbinden

Lernzielkrontrolle

Beantworten Sie in Ihrem Artikel die Lernzielkontrollfragen.

Lernzielkontrollfragen 

1. Wie funktioniert der Primärsensor technisch?
2. Welche Leistungsmerkmale hat der Sensor?
3. Wie funktioniert die Umsetzerschaltung technisch?
4. Wie kommuniziert der Sensor mit dem Arduino?
5. Muss der Sensor kalibriert werden?
6. Wie wird der Messwert in die zu messende physikalische Größe umgerechnet?
7. Was nutzen Sie als Referenz?
8. Benötigt der Sensor eine Kennlinie?
9. Welchen Messbereich hat das Signal am Ende der Messkette?
10. Welche Messunsicherheit und welcher Vertrauensbereich hat das Signal am Ende der Messkette für den gesamten Messbereich?
11. Welche Auflösung hat das Signal am Ende der Messkette? Wodurch wird die Auflösung bedingt?
12. Weist das Signal am Ende der Messkette einen systematischen oder zufälligen Fehler auf?
13. Welche Fehlereinflüsse hat die Messung? Muss z. B. die Temperatur der Messung berücksichtigt werden?

Literatur

Zitieren Sie nach DIN ISO 690:2013-10.

Anhang

• Datenblätter
• Simulink-Modell
• Originaldateien (PAP, Schaltplan,... )

---

→ zurück zum Hauptartikel: BSE Angewandte Informatik SoSe24 | Hausarbeit SoSe24