Spurerkennung mit Kamera und MATLAB: Unterschied zwischen den Versionen
| (12 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 52: | Zeile 52: | ||
=== Vorbereitung === | === Vorbereitung === | ||
Für die Kalibrierung der Kamera in MATLAB kann die [https://www.mathworks.com/help/vision/ug/using-the-single-camera-calibrator-app.html;jsessionid=becc1e38460f878af4774059a381 Camera Calibrator] App verwendet werden. Diese ist auch Teil der [https://de.mathworks.com/products/computer-vision.html Computer Vision Toolbox], welche im Rahmen des Workshops "Spurerkennung (OSE) mit Kamera" benötigt wird. Es empfiehlt sich also, direkt die Toolbox statt nur die App zu installieren. Nach der Installation sollte die Camera Calibrator App in MATLAB sichtbar sein | Für die Kalibrierung der Kamera in MATLAB kann die [https://www.mathworks.com/help/vision/ug/using-the-single-camera-calibrator-app.html;jsessionid=becc1e38460f878af4774059a381 Camera Calibrator] App verwendet werden. Diese ist auch Teil der [https://de.mathworks.com/products/computer-vision.html Computer Vision Toolbox], welche im Rahmen des Workshops "Spurerkennung (OSE) mit Kamera" benötigt wird. Es empfiehlt sich also, direkt die Toolbox statt nur die App zu installieren. Nach der Installation sollte die Camera Calibrator App in MATLAB sichtbar sein. | ||
Um die Kalibrierung durchzuführen, müssen zunächst Bilder eines Schachbrettmusters mit bekannter Kantenlänge gemacht werden. Das Schachbrettmuster kann durch Eingabe des folgenden Befehls im Command Window direkt von MATLAB geöffnet und ausgedruckt werden: | Um die Kalibrierung durchzuführen, müssen zunächst Bilder eines Schachbrettmusters mit bekannter Kantenlänge gemacht werden. Das Schachbrettmuster kann durch Eingabe des folgenden Befehls im Command Window direkt von MATLAB geöffnet und ausgedruckt werden: | ||
| Zeile 64: | Zeile 62: | ||
=== Kalibrierung der Kamera === | === Kalibrierung der Kamera === | ||
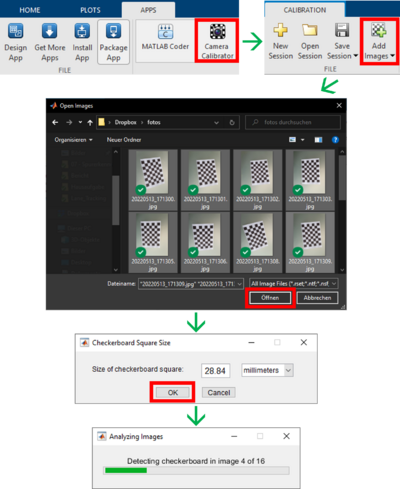
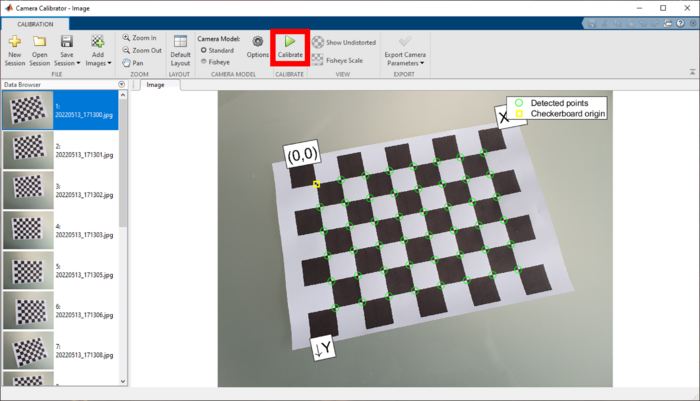
Ein Klick auf das App-Symbol öffnet diese. Um die Fotos hinzuzufügen ist ein Klick auf den Button "Add Images" notwendig. Es öffnet sich ein neues Fenster, in dem die Bilddateien zur Kalibrierung ausgewählt werden müssen. Durch einen Klick auf "Öffnen" erscheint wieder ein neues Fenster. Hier muss die Kantenlänge der Quadrate des Schachbrettmusters eingegeben werden. Diese ist vorher am ausgedruckten Schachbrettmuster abzumessen. Ein Klick auf "OK" bestätigt die Eingabe. Anschließend werden die Bilder analysiert und der App automatisch hinzugefügt. Dabei werden die Eckpunkte des Musters erkannt. | Ein Klick auf das App-Symbol öffnet diese. Um die Fotos hinzuzufügen ist ein Klick auf den Button "Add Images" notwendig. Es öffnet sich ein neues Fenster, in dem die Bilddateien zur Kalibrierung ausgewählt werden müssen. Durch einen Klick auf "Öffnen" erscheint wieder ein neues Fenster. Hier muss die Kantenlänge der Quadrate des Schachbrettmusters eingegeben werden. Diese ist vorher am ausgedruckten Schachbrettmuster abzumessen. Ein Klick auf "OK" bestätigt die Eingabe. Anschließend werden die Bilder analysiert und der App automatisch hinzugefügt. Dabei werden die Eckpunkte des Musters erkannt. Den Workflow zeigt Abb. 1, die Oberfläche der App nach Abschluss der Analyse der Bilder Abb. 2. | ||
[[Datei: | <div align="center"><ul> | ||
<li style="display: inline-block; vertical-align: top;"> [[Datei:Workflow_Einladen_Kamerakalibrierung.png |400px|thumb|center|Abbildung 1: Workflow zum korrekten Einladen der Bilder in die App.]] </li> | |||
<li style="display: inline-block; vertical-align: top;"> [[Datei:Oberflaeche Bilder eingeladen.png |700px|thumb|right|Abbildung 2: Camera Calibrator App nach Einladen der Bilder.]] </li> | |||
</ul></div> | |||
MATLAB nimmt an, dass das ausgedruckte Papier nicht gewellt ist und die Quadrate die angegebene Kantenlänge besitzen. Auf Basis dessen, kann die eigentliche Kalibrierung durchgeführt werden. Dazu muss der Button "Calibrate" angeklickt werden (s. Abb. 2, rotes Rechteck). Die sich ergebene Oberfläche sieht wie in Abb. 3 dargestellt aus. In dieser Ansicht werden für jedes gemachte Bild neben den erkannten Eckpunkten und dem Ursprung des Musters jetzt auch die reprojizierten Punkte als rote Kreuze dargestellt. Außerdem wird der durchschnittliche Fehler in Pixeln für jedes Bild im Tab "Reprojection Errors" oben rechts abgebildet. Unten rechts ist die Lage der Kamera aus Sicht des Papieres (Pattern-centric) sowie die Lage des Papieres aus Sicht der Kamera (Camera-centric) für jedes Bild dargestellt. | |||
[[Datei:Oberflaeche kalibriert.png |700px|thumb|center|Abbildung 3: Camera Calibrator App nach Durchführung der Kalibrierung.]] | |||
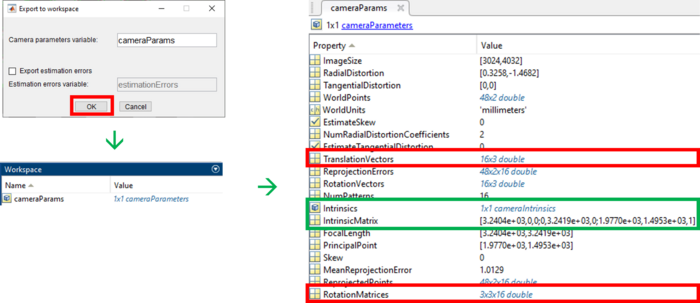
Nachdem die genannten Schritte durchgeführt wurden, können die berechneten Kameraparameter ins Workspace exportiert werden. Dazu genügt ein Klick auf den Button "Export Camera Parameters" (s. Abb. 3, rotes Rechteck). Es öffnet sich ein weiteres Fenster, in der ein Name für die Kameraparameter festgelegt werden muss. Standardmäßig wird hier <code>cameraParams</code> verwendet. Ein Klick auf "OK" bestätigt die Eingabe. Jetzt sind die berechneten Parameter der Kamera im Workspace sichtbar und können z.B. für die Koordinatentransformation genutzt werden. Die Kalibrierung ist damit abgeschlossen. In Abb. 4 ist der Workflow sowie die intrinsischen (grün) und extrinsischen (rot) Kameraparameter dargestellt. | |||
[[Datei:Workflow_Export_Kameraparameter.png |700px|thumb|center|Abbildung 4: Workflow zum Exportieren der Kameraparameter ins Workspace.]] | |||
== Bedeutung der Kalibrierparameter == | == Bedeutung der Kalibrierparameter == | ||
'''Autor:''' | '''Autor: [[Benutzer:Zhiyu Chen | Zhiyu Chen]], [[Benutzer:Michel Grünebaum | Michel Grünebaum]]''' | ||
<br/> | |||
Die Kalibrierparameter bestehen aus zwei Teilen, intrinsische - und extrinsische Parameter. | |||
=== Intrinsische Parameter === | |||
<br/> | |||
{| class="mw-datatable" | |||
! Intrinsische Parameter !! Bedeutung | |||
|- | |||
||FocalLength ||Fokale Länge in x- und y-Richtung in pixel | |||
|- | |||
||PrincipalPoint || Position der optischen Achse in x- und y-Richtung | |||
|- | |||
||RadiaDistortion ||Radiale Verzerrung in x- und y-Richtung | |||
|} | |||
=== Extrinsische Parameter === | |||
<br/> | |||
{| class="mw-datatable" | |||
! Extrinsische Parameter !! Bedeutung | |||
|- | |||
||RotationMatrices||Rotationsmatrix von allen Musterbilder | |||
|- | |||
||TranslationVectors|| Translationsvektor von allen Musterbilder | |||
|- | |||
|} | |||
== Test der Transformation (KOS-Trafo + Perspektive) - Welt zu Bild und Bild zu Welt == | == Test der Transformation (KOS-Trafo + Perspektive) - Welt zu Bild und Bild zu Welt == | ||
| Zeile 479: | Zeile 513: | ||
=== Ansatz 3: [https://de.mathworks.com/help/driving/index.html?s_tid=CRUX_lftnav MATLAB Automated Driving Toolbox] === | === Ansatz 3: [https://de.mathworks.com/help/driving/index.html?s_tid=CRUX_lftnav MATLAB Automated Driving Toolbox] === | ||
Eine weitere Möglichkeit zur Spurerkennung ist die Verwendung von MATLAB-Funktionen aus der [https://de.mathworks.com/help/driving/index.html?s_tid=CRUX_lftnav MATLAB Automated Driving Toolbox]. Eine schöne Einführung in die Thematik bietet die Dokumentation der Funktion <code>[https://de.mathworks.com/help/driving/ref/segmentlanemarkerridge.html segmentLaneMarkerRidge]</code | Eine weitere Möglichkeit zur Spurerkennung ist die Verwendung von MATLAB-Funktionen aus der [https://de.mathworks.com/help/driving/index.html?s_tid=CRUX_lftnav MATLAB Automated Driving Toolbox]. Eine schöne Einführung in die Thematik bietet die Dokumentation der Funktion <code>[https://de.mathworks.com/help/driving/ref/segmentlanemarkerridge.html segmentLaneMarkerRidge]</code>. | ||
''' Hinweise''': | ''' Hinweise''': | ||
| Zeile 486: | Zeile 520: | ||
== Parameterschätzung des Spurpolynoms == | == Parameterschätzung des Spurpolynoms == | ||
'''Autor:''' | '''Autor:''' [[Benutzer:Changlai Bao | Changlai Bao]], [[Benutzer:Nils Koch | Nils Koch]] <br/> | ||
=== Darstellung des Spurpolynoms === | |||
Zunächst schreiben wir das Spurpolynoms: | |||
<math>\hat{y} = a \cdot \hat{x^{2}} + b \cdot \hat{x}+ c</math> | |||
=== Gleichung bekommen === | |||
Um der Parameter a,b,c des Spurpolynoms zu schätzen, müssen wir die folgende Gleichung aufstellen: | |||
<math>V(a,b,c) = \sum_{i=1}^k (y_i-\hat{y_i})^2 = \sum_{i=1}^k(y_i-a \cdot x_i^2-b \cdot x_i - c)^2 </math> | |||
=== Partielle Ableitung bestimmen === | |||
Als Nächstes bestimmen wir die partiellen Ableitungen von a, b und c in Bezug auf diese Funktion: <br> | |||
===== Partielle Ableitung nach a ===== | |||
<math> \frac{\partial V(a,b,c)}{\partial a}=2 \cdot \sum_{i=1}^k(y_i-a \cdot x_i^2-b \cdot x_i - c) \cdot (-x_i^2) </math> | |||
===== Partielle Ableitung nach b ===== | |||
<math> \frac{\partial V(a,b,c)}{\partial b}=2 \cdot \sum_{i=1}^k(y_i-a \cdot x_i^2-b \cdot x_i - c) \cdot (-x_i) </math> | |||
===== Partielle Ableitung nach c ===== | |||
<math> \frac{\partial V(a,b,c)}{\partial c}=2 \cdot \sum_{i=1}^k(y_i-a \cdot x_i^2-b \cdot x_i - c) \cdot (-1) </math> | |||
==== Vereinfachte Gleichung ==== | |||
Da alle 3 partiellen Ableitungen <math>\frac{\partial V(a,b,c)}{\partial a} </math>, <math>\frac{\partial V(a,b,c)}{\partial b} </math>, <math>\frac{\partial V(a,b,c)}{\partial c} </math> gleich Null sind, ergibt sich die folgende vereinfachte Formel: | |||
<math>\quad \overline{y_i x_i^2 } = a \cdot \overline{x_i^4 } + b \cdot \overline{x_i^3 } + c \cdot \overline{x_i^2 } \ </math> <br> | |||
<math>\quad \overline{y_i x_i} = a \cdot \overline{x_i^3 } + b \cdot \overline{x_i^2 } + c \cdot \overline{x_i } \ </math> <br> | |||
<math>\quad \overline{y_i} = a \cdot \overline{x_i^2} + b \cdot \overline{x_i} + c \ </math> | |||
=== Schätzung der Parameter bekommen === | |||
Schließlich können wir die Werte von a, b und c ableiten: | |||
<math> a = {{(\overline{y_i x_i^2} - \overline{y_i} \cdot \overline{x_i^2}) \cdot (\overline{x_i^2} -(\overline{x_i})^2)-(\overline{y_i x_i}- \overline{y_i} \cdot \overline{x_i}) \cdot (\overline{x_i^3}-\overline{x_i} \cdot\overline{x_i^2})} \over {(\overline{x_i^4}-(\overline{x_i^2})^2) \cdot (\overline{x_i^2}-(\overline{x_i})^2)-(\overline{x_i^3}-\overline{x_i} \cdot \overline{x_i^2})^2}}</math> <br> | |||
<math> b = {{\overline{y_i x_i}-\overline{y_i} \cdot \overline{x_i} - a \cdot (\overline{x_i^3} - \overline{x_i} \cdot \overline{x_i^2}) } \over {\overline{x_i^2}-(\overline{x_i})^2}}</math> <br> | |||
<math> c = \overline{y_i} - a \cdot \overline{x_i^2} - b \cdot \overline{x_i} </math> | |||
Damit ist die Schätzung der Parameter des Spurpolynoms abgeschlossen. | |||
== Literatur == | == Literatur == | ||
<references /> | <references /> | ||
Aktuelle Version vom 21. Mai 2022, 13:44 Uhr
Autor: Prof. Dr.-Ing. Schneider, SDE-Team 2022/23
Neue Seite zum Workshop vom 17.05.2022
Im Workshop 7 Spurerkennung (OSE) mit Kamera wurde in nachfolgenden Schritten vorgegangen, die durch die Zweierteams im Nachgang dokumentiert und geprüft werden.
Aufgaben
- Dokumentieren Sie den Workshop so, dass der rote Faden sichtbar ist.
- Die Lösung muss nachvollziehbar sein.
- Dokumentieren Sie Lösungsweg, Lösung und Ergebnisse.
- Diskutieren Sie die Ergebnisse wissenschaftlich.
- Nutzen Sie Unterartikel, falls dies der Übersicht dient.
- Beachten Sie den Artikel Wiki-Artikel_schreiben.
- Achten Sie beim Review auf Inhalt, Lesbarkeit, Orthographie und Nachhaltigkeit.
- Arbeiten sie die Review-Ergebnisse nach Absprache ein.
| # | Aufgabe | Team |
|---|---|---|
| 1 | Kalibrierung der Kamera | Dong, Gosedopp |
| 2 | Bedeutung der Kalibrierparameter | Chen, Grünebaum |
| 3 | Test der Transformation (KOS-Trafo + Perspektive) - Welt zu Bild und Bild zu Welt | Kühnrich, Hernandez Murga |
| 4 | Inverse Perspektiventransformation (IPT) | Hoppe, Pu |
| 5 | Metrischer Test mit Gliedermaßstab (oder Kacheln) | Schonlau, Wei |
| 6 | Segmentierung der Spuren aus den Bildern (Edge Linking, oder Linien im ROI) | Brinkmann, Xia |
| 7 | Parameterschätzung des Spurpolynoms | Koch, Bao |
| 8 | Review der Artikel 1-4 | Müller, Wang |
| 9 | Review der Artikel 5-7 | Kalamani, Schmidt |
Voraussetzungen
Kalibrierung der Kamera
Autoren: Daniel Gosedopp, Zhaolin Dong
Einführung
Die Kamerakalibrierung dient der Ermittlung der extrinsischen und intrinsischen Parameter einer Kamera. Die extrinsischen Parameter sind dabei alle Parameter, welche die Position der Kamera in einem Weltkoordinatensystem beschreiben. Konkret sind das eine Rotationsmatrix, die die Verdrehung des Kamerakoordinatensystems zum Welt-KOS abbildet, sowie ein Translationsvektor, der die translatorische Verschiebung des Kamera-KOS zum Welt-KOS beschreibt. Mit den extrinsischen Parametern lässt sich also eine Koordinatentransformation vom Welt- ins Kamerakoordinatensystem und umgekehrt durchführen. Intrinsische Parameter sind all die Parameter, die den Zusammenhang zwischen dem Kamera-KOS und dem Bild-KOS beschreiben. Dazu zählen radiale Verzerrungsparameter der Linse, die fokale Länge sowie das optische Zentrum in der Bildebene. Mit diesen Parametern lässt sich eine Transformation vom Kamera- ins Bild-KOS und umgekehrt durchführen. Die jeweiligen Transformationen lassen sich auch verknüpfen, sodass ein Punkt im Welt-KOS direkt in das Bild-KOS und umgekehrt transformiert werden kann. Dadurch wird z.B. die kamerabasierte Vermessung von Objekten ermöglicht.
Vorbereitung
Für die Kalibrierung der Kamera in MATLAB kann die Camera Calibrator App verwendet werden. Diese ist auch Teil der Computer Vision Toolbox, welche im Rahmen des Workshops "Spurerkennung (OSE) mit Kamera" benötigt wird. Es empfiehlt sich also, direkt die Toolbox statt nur die App zu installieren. Nach der Installation sollte die Camera Calibrator App in MATLAB sichtbar sein.
Um die Kalibrierung durchzuführen, müssen zunächst Bilder eines Schachbrettmusters mit bekannter Kantenlänge gemacht werden. Das Schachbrettmuster kann durch Eingabe des folgenden Befehls im Command Window direkt von MATLAB geöffnet und ausgedruckt werden:
>> open checkerboardPattern.pdf
Es sind mindestens zwei Bilder notwendig, MATLAB empfiehlt für beste Ergebnisse allerdings 10-20 Bilder. Da die Linsenverzerrung in den Ecken eines Bildes am deutlichsten zum Vorschein kommt, sollten einige Fotos gemacht werden, in denen das Schachbrettmuster entsprechend in den Ecken liegt.
Kalibrierung der Kamera
Ein Klick auf das App-Symbol öffnet diese. Um die Fotos hinzuzufügen ist ein Klick auf den Button "Add Images" notwendig. Es öffnet sich ein neues Fenster, in dem die Bilddateien zur Kalibrierung ausgewählt werden müssen. Durch einen Klick auf "Öffnen" erscheint wieder ein neues Fenster. Hier muss die Kantenlänge der Quadrate des Schachbrettmusters eingegeben werden. Diese ist vorher am ausgedruckten Schachbrettmuster abzumessen. Ein Klick auf "OK" bestätigt die Eingabe. Anschließend werden die Bilder analysiert und der App automatisch hinzugefügt. Dabei werden die Eckpunkte des Musters erkannt. Den Workflow zeigt Abb. 1, die Oberfläche der App nach Abschluss der Analyse der Bilder Abb. 2.
MATLAB nimmt an, dass das ausgedruckte Papier nicht gewellt ist und die Quadrate die angegebene Kantenlänge besitzen. Auf Basis dessen, kann die eigentliche Kalibrierung durchgeführt werden. Dazu muss der Button "Calibrate" angeklickt werden (s. Abb. 2, rotes Rechteck). Die sich ergebene Oberfläche sieht wie in Abb. 3 dargestellt aus. In dieser Ansicht werden für jedes gemachte Bild neben den erkannten Eckpunkten und dem Ursprung des Musters jetzt auch die reprojizierten Punkte als rote Kreuze dargestellt. Außerdem wird der durchschnittliche Fehler in Pixeln für jedes Bild im Tab "Reprojection Errors" oben rechts abgebildet. Unten rechts ist die Lage der Kamera aus Sicht des Papieres (Pattern-centric) sowie die Lage des Papieres aus Sicht der Kamera (Camera-centric) für jedes Bild dargestellt.
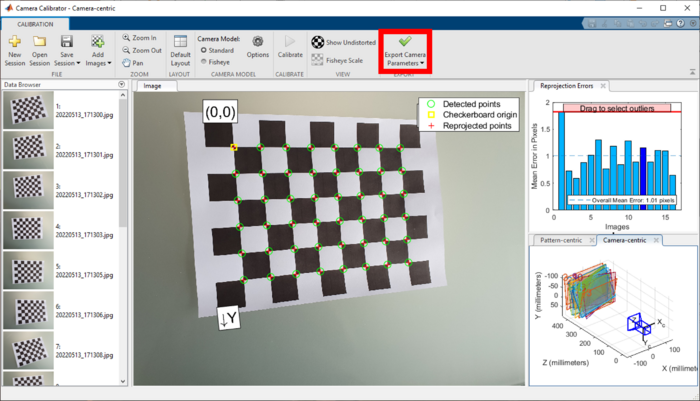
Nachdem die genannten Schritte durchgeführt wurden, können die berechneten Kameraparameter ins Workspace exportiert werden. Dazu genügt ein Klick auf den Button "Export Camera Parameters" (s. Abb. 3, rotes Rechteck). Es öffnet sich ein weiteres Fenster, in der ein Name für die Kameraparameter festgelegt werden muss. Standardmäßig wird hier cameraParams verwendet. Ein Klick auf "OK" bestätigt die Eingabe. Jetzt sind die berechneten Parameter der Kamera im Workspace sichtbar und können z.B. für die Koordinatentransformation genutzt werden. Die Kalibrierung ist damit abgeschlossen. In Abb. 4 ist der Workflow sowie die intrinsischen (grün) und extrinsischen (rot) Kameraparameter dargestellt.
Bedeutung der Kalibrierparameter
Autor: Zhiyu Chen, Michel Grünebaum
Die Kalibrierparameter bestehen aus zwei Teilen, intrinsische - und extrinsische Parameter.
Intrinsische Parameter
| Intrinsische Parameter | Bedeutung |
|---|---|
| FocalLength | Fokale Länge in x- und y-Richtung in pixel |
| PrincipalPoint | Position der optischen Achse in x- und y-Richtung |
| RadiaDistortion | Radiale Verzerrung in x- und y-Richtung |
Extrinsische Parameter
| Extrinsische Parameter | Bedeutung |
|---|---|
| RotationMatrices | Rotationsmatrix von allen Musterbilder |
| TranslationVectors | Translationsvektor von allen Musterbilder |
Test der Transformation (KOS-Trafo + Perspektive) - Welt zu Bild und Bild zu Welt
Autor:
Inverse Perspektiventransformation (IPT)
Autor: Chuan Pu, Sandra Yvonne Hoppe
In diesem Abschnitt wird die Umwandlung einer Videodatei in die Vogelperspektive erläutert. Für die Transformation eines Videos in die Vogelperspektive wird die Inverse Perspektiventransformation Funktion "birdsEyeView" von Matlab Verwendet.
Eingangsparameter
- calibrationSession.CameraParameters.FocalLength
- calibrationSession.CameraParameters.PrincipalPoint
- calibrationSession.CameraParameters.ImageSize
Positionierung Kamera
- Höhe der Kamera vom Boden „height=300“
- Neigungswinkel „pitch = 10“
Blickwinkeleinstellung
- distAhead = 4000
- spaceToOneSide = 800
- bottomOffset = 150
Ausgangsparameter
Die Ausgangsparameter sind die berechneten Werte und die daraus entstandenen Frames. Die Frames werden für die Erstellung des Videos aneinander gehangen und ausgegeben. In der nachfolgenden Datei wird ein gekürztes Video der Inversen Transformation dargestellt.
Im nachfolgenden wird der erstellte Programmcode dargestellt.
%****************************************************************
% Hochschule Hamm-Lippstadt *
%****************************************************************
% Modul : Aufgabe_2_2 *
% *
% Datum : 17.05.2022 *
% *
% Funktion : Erstellung der Vogelperspektive der Spur *
% *
% Implementation : MATLAB R2020a *
% *
% Toolbox : Image Processing Toolbox *
% Computer Vision Toolbox *
% Automated Driving Toolbox *
% *
% Author : Chuan Pu, Sandra Hoppe *
% *
% Bemerkung : Datei Pfade an die Ordnerstruktur anpassen *
% *
% Letzte Änderung : 18.05.2022 *
% *
%***************************************************************/
%% Matlab vorbereiten
close all;
clc;
%% Video laden
addpath('D:\Student\Daten\Vision')
addpath('D:\Student\Kalibrierung_intrinsisch')
video=VideoReader('Rundkurs.mp4');
load('calibrationSession');
%% Parameter der Kamera Laden
focalLength = calibrationSession.CameraParameters.FocalLength
principalPoint = calibrationSession.CameraParameters.PrincipalPoint
imageSize = calibrationSession.CameraParameters.ImageSize
%% Fahrzeugparameter
height = 300; % Höhe der Kamera vom Boden aus in mm
pitch = 10; %Neigungswinkel
%% Blickwinkeleinstellungen
distAhead = 4000;
spaceToOneSide = 800;
bottomOffset = 150;
%% Berechnungen
camIntrinsics = cameraIntrinsics(focalLength,principalPoint,imageSize);
sensor = monoCamera(camIntrinsics,height,'Pitch',pitch);
outView = [bottomOffset,distAhead,-spaceToOneSide,spaceToOneSide];
outImageSize = [NaN,250];
birdsEye = birdsEyeView(sensor,outView,outImageSize);
camIntrinsics = cameraIntrinsics(focalLength,principalPoint,imageSize);
I = readFrame(video);
BEV = transformImage(birdsEye,I);
%% Ausgabe Video
while hasFrame(video)
frame = im2bw(readFrame(video));
birdsImage = transformImage(birdsEye, frame);
imshowpair(frame, birdsImage, 'montage');
end
Metrischer Test mit Gliedermaßstab (oder Kacheln)
Autor:
Segmentierung der Spuren aus den Bildern
Autor: Jiaxiang Xia, Florian Brinkmann
Damit die Fahrbahnmarkierungen korrekt aus dem Bild segmentiert werden können, ist es hilfreich, wenn in dem verwendeten (perspektivtransformierten) Kamerabild keine Bauteile des Fahrzeugs zu sehen sind. Falls noch Elemente des Fahrzeugs im Bild vorhanden sind, sollten diese maskiert und mit schwarz überschrieben werden. Das hier verwendete Beispielvideo aus der Vogelperspektive (Revision 7472) ist bereits so aufbereitet, dass keine Bauteile des Fahrzeugs bei der Segmentierung der Fahrbahnmarkierung stören könnten.
Prinzipiell gibt es verschiedene Möglichkeiten die drei Fahrbahnmarkierungen zu segmentieren. Entweder man "erkennt" alle drei Markierungen aus dem Kamerabild oder es wird nur eine Fahrbahnmarkierung "erkannt". Von dieser Markierung aus können dann bei einer festen Fahrbahnbreite alle anderen Markierungen berechnet werden. Zur Segmentierung der Fahrbahnmarkierungen aus dem perspektivtransformierten Kamerabild gibt es verschiedene Ansätze, die nachfolgend erläutert werden sollen.
Ansatz 1: Spurverfolgung
Beim ersten Ansatz wird für jeden Frame eines Videos zunächst der Startpunkt einer Fahrbahnmarkierung am unteren Bildrand gesucht. Im Anschluss daran wird von diesem Startpunkt aus die weiße Linie bis zum Ende mit Hilfe der 8er-Nachbarschaften verfolgt. Nachfolgend ist eine beispielhafte Implementierung hinterlegt, die rechts ausgeklappt werden kann.
Suche nach dem Startpunkt der Fahrbahnmarkierung
Zunächst muss der Startpunkt der Fahrbahnmarkierung am unteren Bildrand gesucht werden. Dazu wird im unten dargestellten Code der Suchbereich eingegrenzt, sodass die linke Spur nur in einem Bereich links der Mitte und die rechte Fahrbahnmarkierung in einem Bereich rechts der Mitte gesucht wird. Die Mittelspur wird nicht gesucht, da diese später aus den beiden äußeren Fahrbahnmarkierungen berechnet wird. Ist in der untersten Zeile kein weißes Pixel einer Fahrbahnmarkierung vorhanden, sucht der Algorithmus in einer Zeile weiter oben nach dem Startpunkt der Linie.
function [xLinks, xRechts, yLinks, yRechts] = sucheStartwert(aBild)
%SUCHESTARTWERT vom unteren Bildrand aus die Startpositionen der linken und
%der rechten weißen Kurve.
%
% Syntax:
% [xLinks, xRechts, yLinks, yRechts] = sucheStartwert(aBild)
%
% Beschreibung:
% Sucht den Anfang der weißen Fahrbahnmarkierungen/Kurven.
%
% Eingangswerte:
% aBild: Binärbild mit weißen Kurven
%
% Rückgabewerte:
% xLinks: Vektor mit x-Positionen der linken Kurve
% yLinks: Vektor mit y-Positionen der linken Kurve
% xRechts: Vektor mit x-Positionen der rechten Kurve
% yRechts: Vektor mit y-Positionen der rechten Kurve
%
% Beispiel:
% [xLinks, xRechts, yLinks, yRechts] = sucheStartwert(aFrame)
%*************************************************************************\
%
% Modul : segmentiereFahrbahnmarkierungen.m
%
% Datum : 13.05.2022
%
% Implementierung : MATLAB R2019b
%
% Toolbox :
%
% Autor : Brinkmann, Florian
%
% Bemerkung :
%
% Letzte Änderung : 13.05.2022
%
%************************************************************************/
% Bildgröße bestimmen
[M,N] = size(aBild);
% Boolean-Variablen, um bei gefundenem Startpunkt die Suche zu beenden
linksGefunden = 0;
rechtsGefunden = 0;
% Suchbereich
linkeGrenze = floor(N/3);
Mitte = floor(N/2);
rechteGrenze = floor(N*2/3);
% Suche nach linkem Startwerk links der Mitte
for m = M:-1:1
for n = linkeGrenze:1:Mitte-60
if (linksGefunden == 0) && aBild(m,n) == 1
xLinks = n;
yLinks = m;
linksGefunden = 1;
end
% Suche abbrechen, falls Pixel gefunden
if (linksGefunden == 1)
break
end
end
% Suche abbrechen, falls Pixel gefunden
if (linksGefunden == 1)
break
end
end
% Suche nach rechtem Startwerk rechts der Mitte
for m = M:-1:1
for n = rechteGrenze:-1:Mitte
if (rechtsGefunden == 0) && aBild(m,n) == 1
xRechts = n;
yRechts = m;
rechtsGefunden = 1;
end
% Suche abbrechen, falls Pixel gefunden
if (rechtsGefunden == 1)
break
end
end
% Suche abbrechen, falls Pixel gefunden
if (rechtsGefunden == 1)
break
end
end
end
Verfolgen der Fahrbahnmarkierung
Nachdem die Startpunkte der Fahrbahnmarkierungen gefunden wurden, kann der Verlauf der Markierungen im Bild herausgesucht werden. Wie das nachfolgende Code-Beispiel zeigt, kann dabei mit Hilfe der Nachbarschaftsbeziehungen überprüft werden, ob im Umfeld ein weiters Pixel weiß ist. Damit der Algorithmus am Ende der Fahrbahnmarkierung nicht wieder zum Startpunkt zurück sucht, werden nur die Nachbarn betrachtet, die vor oder seitlich des aktuellen Pixels sind.
function [x, y, aBildSegmentiert] = spurVerfolgen(aBild, xStart, yStart, aBildSegmentiert)
%SPURVERFOLGEN sucht von einem Startpunkt den Verlauf einer weißen Kurve in
%einem Binärbild.
%
% Syntax:
% [x, y, aBildSegmentiert] = spurVerfolgen(aBild, xStart, yStart)
% [x, y, aBildSegmentiert] = spurVerfolgen(aBild, xStart, yStart, aBildSegmentiert)
%
% Beschreibung:
% Verfolgt eine weiße Kurve.
%
% Eingangswerte:
% aBild: Binärbild mit weißer Kurve
% xStart: x-Position, bei der die weiße Kurve beginnt
% yStart: y-Position, bei der die weiße Kurve beginnt
% aBildSegmentiert: Bild mit segmentierter Kruve, default: Schwarzbild
%
% Rückgabewerte:
% x: Vektor mit x-Positionen der Kurve
% y: Vektor mit y-Positionen der Kurve
% aBildSegmentiert: Bild mit segmentierter Kruve
%
% Beispiel:
% [x, y] = spurVerfolgen(aFrame, 20, 500)
%*************************************************************************\
%
% Modul : segmentiereFahrbahnmarkierungen.m
%
% Datum : 13.05.2022
%
% Implementierung : MATLAB R2019b
%
% Toolbox :
%
% Autor : Brinkmann, Florian
%
% Bemerkung :
%
% Letzte Änderung : 13.05.2022
%
%************************************************************************/
% Bildgröße bestimmen
[M,N] = size(aBild);
% Default-Schwarzbild (Ergebnisbild) erzeugen
if nargin < 4
aBildSegmentiert = zeros(M,N);
end
% Startwerte in Egbenisvektor ablegen
x(1) = xStart;
y(1) = yStart;
aBildSegmentiert(y(1), x(1)) = 1;
% Schleife über alle Zeilen des Bildes
for i = 1:M-1
% Nächstes weißes Pixel suchen
[a,b] = naechstesPixel(aBild,x(i),y(i),1);
if a == -1 || b == -1 % Kein weißes Pixel gefunden
break
disp('Linie zu Ende')
else % weißes Pixel gefunden
% Koordinaten in Ergebnisvektor ablegen
x(i+1) = a;
y(i+1) = b;
aBildSegmentiert(b,a) = 1;
end
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [x,y] = naechstesPixel(aBild, x0, y0, sollWert)
%NAECHSTESPIXEL sucht von einem Startpunkt das nächste Pixel. Zunächst wird
%in der nächsten Zeile gesucht, wird dort kein weißes Pixel gefunden wird
%auch links und rechts des Startpunkts gesucht.
%
% Syntax:
% [x,y] = naechstesPixel(aBild, x0, y0)
% [x,y] = naechstesPixel(aBild, x0, y0, sollWert)
%
% Beschreibung:
% Es werden weiße Pixel in der Umgebung gesucht.
%
% Eingangswerte:
% aBild: Binärbild, in dem sich eine weiße Kurve befindet
% x0: Starpunkt für Suche in x-Richtung
% y0: Startpunkt für Suche in y-Richtung
% sollWert: Wert für weißes Pixel, default: 1
%
% Rückgabewerte:
% x: x-Position des nächsten weißen Pixel
% y: y-Position des nächsten weißen Pixel
%
% Beispiel:
% [x,y] = naechstesPixel(aFrame, 20, 500)
% [x,y] = naechstesPixel(aFrame, 20, 500, 1)
%*************************************************************************\
%
% Modul : segmentiereFahrbahnmarkierungen.m
%
% Datum : 13.05.2022
%
% Implementierung : MATLAB R2019b
%
% Toolbox :
%
% Autor : Brinkmann, Florian
%
% Bemerkung :
%
% Letzte Änderung : 13.05.2022
%
%************************************************************************/
% Default-Werte
if nargin <4
sollWert = 1;
end
% Abfang, falls Ränder erreicht
if y0 == 1 || x0 == 1
x = -1;
y = -1;
return
end
% Suche nach weißem Pixel in der Umgebung
if aBild(y0-1, x0) == sollWert % Pixel oben
x = x0;
y = y0-1;
elseif aBild(y0-1, x0-1) == sollWert % Pixel oben links
x = x0-1;
y = y0-1;
elseif aBild(y0-1, x0+1) == sollWert % Pixel oben rechts
x = x0+1;
y = y0-1;
elseif aBild(y0, x0-1) == sollWert % Pixel links
x = x0-1;
y = y0;
elseif aBild(y0, x0+1) == sollWert % Pixel rechts
x = x0+1;
y = y0;
% Nach unten, also zurück muss nicht gesucht werden
% elseif aBild(y0+1, x0) == sollWert % Pixel unten
% x = x0;
% y = y0+1;
% elseif aBild(y0+1, x0-1) == sollWert % Pixel unten links
% x = x0-1;
% y = y0+1;
% elseif aBild(y0+1, x0+1) == sollWert % Pixel unten rechts
% x = x0+1;
% y = y0+1;
else % Falls kein weißes Pixel gefunden wurde
x = -1;
y = -1;
end
end
Ansatz 2: Kantenerkennung
Neben der Spurverfolgung gibt es auch die Möglichkeit mittels Kantenerkennung die Fahrbahnmarkierungen in einem Frame des Videos zu segmentieren. Dazu wird zunächst der Sobel-Operator genutzt, um ein Bild zu erzeugen, indem nur die Kanten sichtbar sind. Hierzu kann die MATLAB Funktion edge[1] verwendet werden. Für jede Fahrbahnmarkierungen erhält man durch die Kantenerkennung zwei Kanten, einmal den Übergang von schwarz zu weiß und einmal den Übergang von weiß zu schwarz. Um die doppelten Kanten zu entfernen muss dass Bild zeilenweise durchlaufen werden. Hierbei überprüft man den Abstand zwischen zwei Kanten. Ist dieser Abstand kleiner als 6 Pixel kann davon ausgegangen werden, dass die beiden Kanten zu einer Fahrbahnmarkierung gehören. Entweder löscht man dann beide Kanten und erzeugt eine neue Kante in der Mitte oder man löscht eine Kante und nutzt die verbleibende Kante als Position der Fahrbahnmarkierung.
Ansatz 3: MATLAB Automated Driving Toolbox
Eine weitere Möglichkeit zur Spurerkennung ist die Verwendung von MATLAB-Funktionen aus der MATLAB Automated Driving Toolbox. Eine schöne Einführung in die Thematik bietet die Dokumentation der Funktion segmentLaneMarkerRidge.
Hinweise:
- Zur Nutzung der Funktion müssen die Kameraparameter bekannt sein.[2]
- Die Dokumentation verwendet den Befehl
im2gray. Dieser ist allerdings erst ab der MATLAB R2020b verfügbar. In vorherigen Versionen kann ein RGB-Bild mit der Funktionrgb2grayin ein Grauwertbild umgewandelt werden.
Parameterschätzung des Spurpolynoms
Autor: Changlai Bao, Nils Koch
Darstellung des Spurpolynoms
Zunächst schreiben wir das Spurpolynoms:
Gleichung bekommen
Um der Parameter a,b,c des Spurpolynoms zu schätzen, müssen wir die folgende Gleichung aufstellen:
Partielle Ableitung bestimmen
Als Nächstes bestimmen wir die partiellen Ableitungen von a, b und c in Bezug auf diese Funktion:
Partielle Ableitung nach a
Partielle Ableitung nach b
Partielle Ableitung nach c
Vereinfachte Gleichung
Da alle 3 partiellen Ableitungen , , gleich Null sind, ergibt sich die folgende vereinfachte Formel:
Schätzung der Parameter bekommen
Schließlich können wir die Werte von a, b und c ableiten:
Damit ist die Schätzung der Parameter des Spurpolynoms abgeschlossen.